Thermodynamique
Chaleur et température Lorsqu'on fournit de l'énergie thermique à un corps, on lui fournit de la chaleur. La chaleur est une forme d'énergie qui, dans le SI, se mesure en joules (J).
Qu'arrive-t-il quand un corps reçoit cette forme d'énergie?
Premièrement, on constate que sa température augmente; on peut s'apercevoir de cette augmentation de température en le touchant de la main, mais un thermomètre permet une évaluation plus précise.
Deuxièmement, les physiciens ont découvert que les atomes du corps deviennent plus agités : à l'intérieur d'un solide, ils vibrent rapidement sur place, tandis que, dans un gaz, ils se déplacent de façon désordonnée et à grande vitesse.
Pour une quantité de chaleur donnée, l'augmentation de température dépend de la masse du corps et du matériau dont il est composé. Par exemple, si on fournit 100 kilojoules de chaleur à 1 kg d'eau, sa température augmente de 24 °C.
La même chaleur transmise à 1 kg de cuivre provoque une augmentation de température de 263 °C. On voit donc que chaleur et température sont deux choses bien différentes. Si l'on soustrait de l'énergie thermique d'un corps, sa température diminue.
Cependant, bien qu'il n'existe aucune limite supérieure à la température qu'on peut atteindre (on atteint déjà des millions de degrés), il existe une limite inférieure que l'on ne peut dépasser. Cette limite en deçà de laquelle un corps ne peut plus être refroidi s'appelle le zéro absolu. Elle correspond à une température de 0 kelvin ou -273,15 °C.
Au zéro absolu, la vibration des atomes cesse et plus rien ne bouge sauf les électrons qui continuent à tourner autour des noyaux atomiques.
Échelles de température Bien que l'unité SI de température soit le kelvin, le degré Celsius (°C) peut, lui aussi, être employé avec le SI.
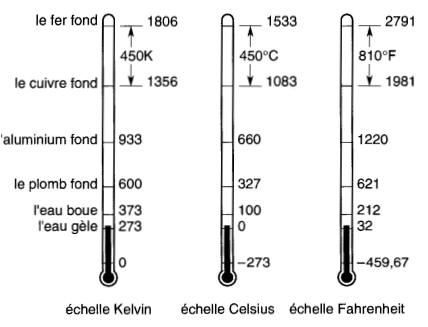
Les échelles de la Fig. 1-18 donnent la relation entre ces deux méthodes de mesure de la température. On y voit aussi l'échelle en degrés Fahrenheit.
Figure 1-18 Échelles de température.

Lorsque la température d'un corps est donnée en kelvins, on dit que cela représente la température absolue du corps. On obtient la température absolue en ajoutant 273,15° à la température exprimée en °C.
Chaleur requise pour chauffer un corps
On a vu que l'augmentation de température d'un corps dépend de la chaleur qu'il reçoit, du matériau dont il est constitué, et de sa masse.
C'est ce qu'exprime la relation suivante:
Q = mcθ
où
Q = quantité de chaleur, en joules [J]
m = masse du corps, en kilogrammes [kg]
c = chaleur massique, en J/(kg.°C), grandeur qui dépend du matériau
θ = variation de la température en °C ou en kelvins
La chaleur massique de plusieurs substances est donnée au tableau Propriétés des conducteurs (et isolants) usuels.
Exemple 1-11
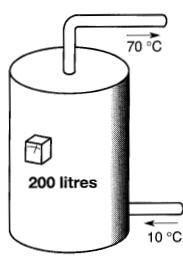
Calculer la quantité (le chaleur requise pour augmenter la température de 200 litres d'eau de 10°C à 70°C si le réservoir est parfaitement isolé (Fig.1-19).
La chaleur massique de l'eau est
c = 4180 J/(kg.°C)
Figure 1-19 Voir exemple 1-11
Solution
Puisqu'un litre d'eau possède une masse de 1 kg, le nombre de joules requis est:
Q = mcθ
= 200 x 4180 x (70 - 10) = 50 160 000 joules = 50,2 MJ
Rendement d'une turbine à vapeur
La puissance mécanique que peut fournir une turbine à vapeur dépend, non seulement de la chaleur qu'on lui fournit, mais aussi de la température d'entrée T1 et de la température de sortie T2 de la vapeur.
En effet, le rendement théorique maximal d'une turbine à vapeur est donné par l'équation de Carnot:
η = 1 - (T2 / T1) (1-18)
où
η = rendement
T1 = température absolue de la vapeur à l'entrée de la turbine, en kelvins [K]
T2 = température absolue de la vapeur à la sortie de la turbine, en kelvins [K]
Afin d'obtenir le maximum d'énergie mécanique pour une quantité de chaleur (joules) donnée, on cherche à augmenter T1 et à diminuer T2.
La température minimale T2 est imposée par la température ambiante, située habituellement aux environs de 20 °C, soit 293 kelvins.
La température maximale T2 est limitée par la résistance des matériaux aux hautes températures et aux hautes pressions.
Dans les turbines modernes, cette température est d'environ 500 °C, soit 773 kelvins, ce qui permet un rendement théorique maximal de
η = 1 - (293 / 773) = 0.62 ou 62%
En fait, par suite des pertes dans la chaudière et d'autres pertes parasites, et parce que la température minimale est toujours supérieure à la température ambiante, le rendement global d'une centrale thermique dépasse rarement 40 %.
Tous les moteurs thermiques convertissant l'énergie thermique en énergie mécanique sont ainsi limités au rendement théorique maximal donné par l'équation (1-18).
Les moteurs à essence, les moteurs diésel et les moteurs à réaction brûlent le combustible dans le moteur même, élevant ainsi la température des gaz à T1.
Puisque la température d'échappement T2 est sensiblement supérieure à la température ambiante, ces moteurs sont limités par les mêmes contraintes que la turbine à vapeur; leur rendement est donc encore plus faible.
Transport de la chaleur
Plusieurs problèmes en électrotechnique sont rattachés au refroidissement adéquat des dispositifs et des machines. Cela exige une connaissance du mécanisme de transport de la chaleur d'un corps à un autre.
Dans les sections qui suivent nous donnons un bref aperçu du transport de la chaleur:
(1) par radiation, (2) par conduction et (3) par convection.
Nous donnons aussi quelques équations simples qui permettent d'évaluer approximativement la perte de chaleur et l'échauffement de l'équipement électrique.
Propagation de la chaleur par radiation
Nous sommes tous conscients de la chaleur produite par les rayons du soleil.
Cette énergie radiante possède les mêmes propriétés que la lumière, passant facilement à travers le vide qui sépare la terre du soleil.
L'énergie solaire se transforme en chaleur uniquement lorsque les rayons rencontrent un corps solide comme les objets ou les êtres vivants se trouvant à la surface de la terre.
Les scientifiques ont constaté que, comme le soleil, tout corps rayonne de l'énergie. La quantité d'énergie dégagée dépend de la température de ce corps.
Inversement, tout corps reçoit, des objets qui l'entourent, une quantité d'énergie radiante qui dépend de leur température.
Il y a donc un échange continuel d'énergie radiante entre les corps matériels, chacun d'eux se comportant comme un soleil miniature.
Un équilibre s'établit lorsque la température d'un corps est la même que celle des objets qui l'entourent; le corps rayonne alors autant d'énergie qu'il en reçoit, et sa radiation nette est nulle.
Par ailleurs, si le corps est plus chaud que son environnement, il perd de la chaleur par radiation, même s'il est situé dans le vide parfait.
Calcul des pertes par radiation
Soit un corps de surface A, à une température Tt, placé dans une enceinte dont les parois sont à la température T2.
La puissance nette P irradiée par le corps est donnée par la formule:
P = kA (T14 -T24 ) (1-19)
où
P = puissance
irradiée, en watts [W]
A = surface du corps, en mètres carrés [m2]
T1 = température absolue du corps, en kelvins [K]
T2 = température absolue des parois, en kelvins [K]
k = constante de radiation [W/(m2.K4)]
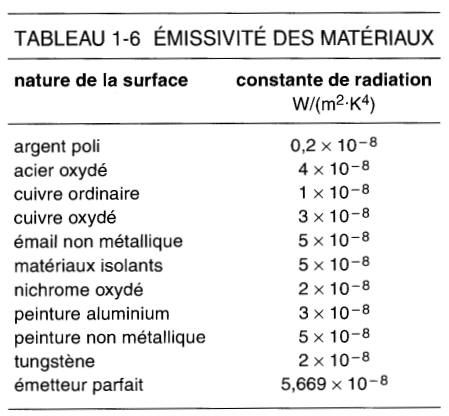
Le tableau 1-6 donne les valeurs de la constante de radiation k pour quelques surfaces que l'on peut rencontrer dans le calcul des pertes par radiation.
Exemple 1-12
Une résistance cylindrique de 20 cm de long, 3 cm de diamètre a une superficie de 188 cm² (Fig. 1-20).
Figure 1-20 Voir exemples 1-12 et 1-14.
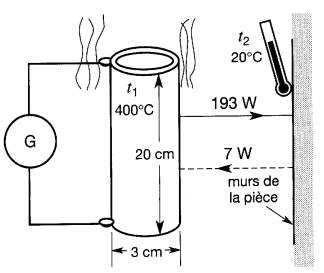
Si elle fonctionne à une température de 400°C lorsqu'on la dépose dans une pièce dont la température ambiante est 20°C, calculer la puissance nette dégagée par radiation.
Prendre k = 5 x 10-8.
Solution
Calculons d'abord les températures absolues T1 et T2.
T1 = t1 + 273 = 400 + 273 = 673 K
T2 = t2 + 273 = 20 + 273 = 293 K
On obtient d'après la formule:
P=kA(T14 -T24) = 5 x 10-8 x 0,0188(6734 - 2934 ) = 193 -7 =186W
La résistance dissipe 186 W par radiation.
Transport par conduction
Si l'on chauffe une des extrémités d'un barreau d'acier avec une flamme (Fig. 1-21), on constate que la chaleur se propage graduellement vers l'autre extrémité.
Figure 1-21 Transport de la chaleur par conduction, par convection et par radiation.
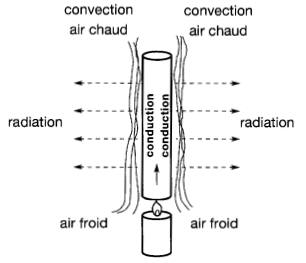
On dit alors qu'il y a propagation de la chaleur par conduction; les atomes du barreau situé près de la flamme deviennent plus agités et leur agitation thermique se transmet de proche en proche aux atomes voisins, jusqu'à l'autre bout du barreau.
Le transport de la chaleur par conduction se fait plus ou moins bien selon la nature de la substance.
Ainsi, le cuivre est un meilleur conducteur que l'acier alors que les isolants sont reconnus comme étant de très mauvais conducteurs de la chaleur.
Calcul des pertes par conduction La perte de chaleur par conduction fait intervenir la conductivité thermique λ du matériau transportant la chaleur.
L'unité SI de conductivité thermique est le watt par mètre-degré Celsius [W/(m.°C)]. Les tableaux Propriétés des matériaux isolants et Propriétés des conducteurs (et isolants) usuels donnent la conductivité thermique λ pour plusieurs matériaux utilisés en électrotechnique.
Soit une plaque d'un matériau ayant une épaisseur d et dont les deux faces ont une surface A.
Si l'on connaît la valeur de la conductivité thermique du matériau et les températures t1 et t2 respectives des deux faces, on peut calculer la quantité de chaleur qu'il transporte en utilisant la formule suivante (voir la Fig. 1-22):
P = λA (t1 -t2) / d (1-20)
où
P = puissance (en
chaleur) transmise, en watts [W]
λ = conductivité thermique du matériau, en watts par mètre-degré Celsius [W/(m.°C)]
A = surface du matériau, en mètres carrés [m²]
t1, t2 = températures respectives des deux faces, en degrés Celsius [°C]
d = épaisseur du matériau, en mètres [m]
Figure 1-22 Transport de la chaleur par conduction.
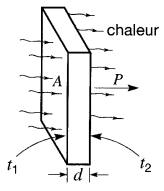
La chaleur transportée dépend de la différence de température (t1 - t2) entre les deux faces. De plus, elle est toujours transportée de la face la plus chaude vers la face la moins chaude.
Exemple 1-13
La différence de température entre les deux faces d'une plaque de mica ayant les dimensions données à la Fig. 1-23 est de 50 °C.
Figure 1-23 Voir exemple 1-13.
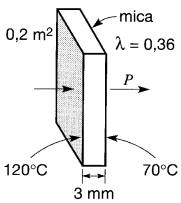
Calculer la puissance transmise sous forme de chaleur, en watts.
Solution
D'après le tableau Propriétés des matériaux isolants en appendice, la conductivité thermique du mica est 0,36 W/(m.°C).
La chaleur transmise vaut donc:
P = λA (t1 -t2) / d = 0,36 x 0,02 (120-70) / 0,003 = 120 W
Transport de la chaleur par convection
Dans la Fig. 1-21, un barreau de fer, dont une extrémité est chauffée par une flamme, transmet la chaleur par conduction à l'autre extrémité.
En même temps, une partie de la chaleur transmise se perd par radiation. De plus, l'air se trouvant en contact avec le barreau se réchauffe et, devenant ainsi plus léger, il se met à monter comme dans une cheminée.
En montant, l'air chaud est aussitôt remplacé par de l'air frais qui, à son tour, est réchauffé. Il se produit donc une circulation d'air autour du barreau qui perd ainsi une autre partie de la chaleur par convection.
Le même phénomène se produit lorsque l'on place un corps chaud dans un liquide comme de l'huile. L'huile en contact avec le corps se réchauffe, créant ainsi des courants de convection qui suivent le chemin tracé à la Fig. 1-24.
Figure 1-24 Courants de convection dans un liquide
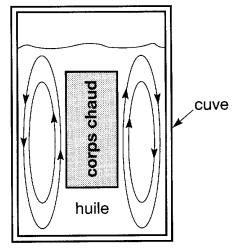
Lorsque l'huile arrive en contact avec la cuve métallique, elle se refroidit et, devenant plus lourde, elle glisse vers le bas pour ensuite remonter de nouveau le long du corps chaud. La chaleur dégagée par le corps chaud se trouve ainsi transportée par les courants de convection vers la cuve extérieure.
La chaleur se dégage particulièrement bien lorsqu'on utilise un ventilateur pour forcer une circulation plus rapide d'air frais.
Ce mode de transport de la chaleur par convection forcée est employé dans la plupart des moteurs électriques pour assurer un refroidissement efficace.
Calcul des pertes par convection
La perte de chaleur par convection d'un corps à l'air libre est donnée par la formule approximative :
P = 3A (t1 - t2 )1.25 (1-21)
où
P = chaleur dissipée
par convection, en watts [W]
A = surface du corps, en mètres carrés [m²]
t1 = température de la surface [°C]
t2 = température de l'air ambiant [°C]
Exemple 1-14
Calculer la perte de chaleur par convection pour la résistance de la Fig 1-20
Solution
On a:
t1 = 400 °C
t2 = 20 °C
A = 188 cm² = 0,0188 m²
d'où
P = 3A (t1 - t2)1.25 = 3 x 0,0188 (400 - 20)1.25
= 95 watts
En considérant les pertes par radiation calculées dans l'exemple 1-12, la résistance perd donc au total
P = (186 + 95) = 291 W
Remarquer que la chaleur dissipée par radiation est deux fois plus grande que celle dissipée par convection.
Dans le cas d'une convection forcée, telle que celle produite par un ventilateur, la quantité de chaleur transportée est donnée par:
P = 1280D (t2 - t1) (1-22)
où
P = chaleur transportée par convection forcée [W]
D = débit d'air refroidissant [m³/s]
t1 = température de l'air à l'entrée [°C]
t2 = température de l'air à la sortie [°C]
1280 = constante tenant compte des unités
Exemple 1-15
Un ventilateur utilisé pour refroidir un moteur de 750 kW fait circuler 240 m³/min d'air frais dans la machine.
Si la température de l'air â l'entrée est de 22 °C et de 31 °C à la sortie, calculer les pertes approximatives dans le moteur.
Solution
Les pertes de la machine sous forme de chaleur sont :
P = 1280D(t2 - t1) = 1280 x 240/60 (31 - 22) = 46 080 W = 46 kW
Conversion des unités
Au cours des années, les unités utilisées en électricité, en mécanique et en thermodynamique ont évolué graduellement pour devenir aujourd'hui les unités SI.
Toutefois, on doit à l'occasion convertir les anciennes unités en unités SI. C'est alors que les tables de conversion fournies en appendice au tableau Conversion des unités de mesure s'avèrent particulièrement utiles.
Elles sont composées de boîtes rectangulaires représentant diverses unités. Les boîtes sont réunies par des flèches portant chacune un chiffre. Pour passer d'une unité à une autre, on doit traverser une, deux ou plusieurs flèches.
On applique alors la règle suivante:
Lorsqu'on circule dans le sens de la flèche, on multiplie par le chiffre associé ; lorsqu'on circule dans le sens contraire, on divise. Les exemples suivants illustrent la méthode.
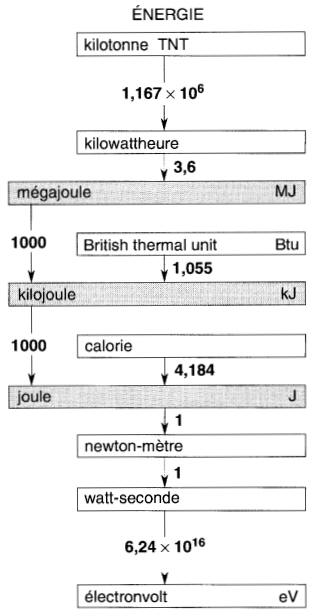
Figure 1-25 Table servant à la conversion des unités d'énergie.
Exemple 1-16
Convertir 7 kilowattheures en joules.
Solution
En se référant à la table de conversion intitulée ÉNERGIE (Fig. 1-25), on doit traverser trois flèches afin de passer de kilowattheure à joule; en appliquant la règle, on obtient:
7 kW.h = 7 x 3,6 x 1000 x 1000 J = 25,2 x 106J = 25,2 MJ
Exemple 1-17
Convertir 777 calories en kilowattheures.
Solution
En utilisant la même table, on doit traverser quatre flèches, dont trois dans le sens opposé à la flèche.
On obtient donc:
777 calories = 777 x 4,184 - 1000 - 1000 - 3,6 = 9,03 x 10-4 kW. h
Mesures en valeurs relatives, système P.U.
Les unités de mesure SI mentionnées à la section 1.34 servent à exprimer la valeur d'une grandeur.
Par exemple, la masse est exprimée en kilogrammes, la puissance en watts et la tension en volts. Toutefois, on peut souvent mieux apprécier l'amplitude d'une grandeur en la comparant à une autre grandeur semblable.
Supposons, par exemple, que le poids moyen d'un adulte soit 60 kg. On peut alors comparer le poids de n'importe quel individu à ce poids moyen.
Ainsi, une personne pesant 72 kg aurait un poids relatif de 72/60 = 1,2.
Une autre personne pesant 52 kg aurait un poids relatif de 52/60 = 0,87.
Afin de signaler qu'il s'agit bien d'une mesure relative, on ajoute le symbole p.u. après le chiffre.
Le symbole «p.u.» est une abréviation de «par unité» ; en anglais «per unit».
Ainsi, les poids des deux individus exprimés en valeurs relatives sont respectivement 1,2 p.u. et 0,87 p.u.
Le système de mesure p.u. a l'avantage de donner le poids d'une personne par rapport à un étalon convenable, appelé base du système. Dans notre cas, le poids de base est 60 kg.
Ainsi, si l'on indique qu'un boxeur poids lourd pèse 1,7 p.u., on remarque immédiatement que son poids est bien supérieur à la moyenne et que, de plus, sa masse est de 1,7 x 60 = 102 kg.
Noter que la valeur d'une grandeur exprimée en p.u. est un simple nombre sans dimension.
Ainsi, il est faux de dire que notre boxeur pèse 1,7 kg. Son poids est 1,7 unités, l'unité choisie étant 60 kg.
En général, un système de mesure p.u. utilise une ou plusieurs grandeurs comme bases de comparaison. Dans cette section, nous aurons à choisir des bases convenables principalement pour la puissance, la tension et la vitesse de rotation.
Système p.u. à base unique
Si l'on choisit une seule grandeur comme étalon, on dit que ce système p.u. possède une seule base.
La base peut être une puissance, une tension ou toute autre grandeur.
Supposons, par exemple, que trois moteurs possèdent des puissances de 25 kW, 40 kW et 150 kW. Adoptons comme base une puissance PB de 50 kW.
Les puissances relatives sont calculées comme suit:
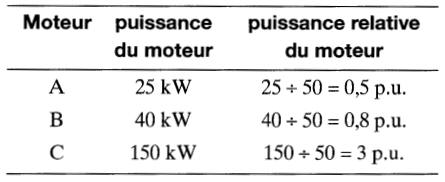
On pourrait aussi bien choisir une base de 15 kW.
Dans ce cas les puissances relatives seraient:
25 kW / 15 kW = 1,67 p.u.
40 kW / 15 kW = 2,67 p.u.
150 kW / 15 kW =10p.u.
Il est évident que pour trouver la valeur réelle d'une grandeur exprimée en p.u. on doit connaître la valeur de la base.
Cependant, même si on ne la connaît pas, la valeur en p.u. est une indication de sa valeur relative, ce qui est souvent fort utile.
Exemple 1-18
Dans un système p.u., on choisit une longueur de hase Lbase = 6 m.
Déterminer la valeur en p.u. des grandeurs suivantes:
a) une longueur de 9 m
b) une surface de 28 m²
C) un volume de 24 m³
Solution
a) la longueur en p.u. de 9 m est:
Lp.u. = Lréel / Lbase = 9m / 6 m = 1,5 p.u.
b) afin de calculer la valeur relative de la surface, on doit d'abord trouver la valeur de la surface de base:
Sbase = Lbase x Lbase = 6 m x 6 m = 36 m²
donc, la valeur en p.u. de 28 m² est:
Sp.u. = Sréel / Sbase = 28 m² / 36 m² = 0.78 p.u.
c) Sachant que Lasse = 6 m, on trouve que le volume de base est:
Vbase = 6m x 6m x 6m=216m³
La valeur relative de 24m³ est donc:
Vp.u. = Vréel / Vbase = 24m³ / 216m³ = 0.11 p.u.
Système de mesure p.u. à deux bases
Système de mesure p.u. à deux bases En électrotechnique, le système p.u. devient particulièrement utile lorsqu'on utilise deux bases.
Les bases sont habituellement une tension EB et une puissance PB.
Ainsi, la base de tension pourrait être de 4 kV et la base de puissance, 500 kW. On peut choisir les bases indépendamment l'une de l'autre.
Il est important de noter que dès que l'on a choisi les valeurs de base EB et PB, le courant de base IB et l'impédance de base ZB sont aussitôt imposés par les lois de l'électricité.
On aura ainsi:
IB = PB / EB (1-23) et ZB = EB / IB (1-24)
Exemple 1-19
Une source possède une tension nominale de 4 kV et une puissance nominale de 500 kW.
Connaissant ces deux grandeurs de base, calculer les valeurs du courant de base et de l'impédance de base.
Solution
Le courant de base est:
I = PB / EB = 500 000 W / 4000 V = 125 A
et l'impédance de base est:
Z = EB / IB = 4000 V / 125 A= 32Ω
Par conséquent, ce système p.u. à deux bases donne en réalité un système à quatre bases.
Système de mesure p.u. à trois bases
Lors de l'étude des machines électriques rotatives, on sélectionne trois grandeurs de base :
(1) la puissance, (2) la tension, et (3) la vitesse de rotation.
Dans ce cas, on choisit comme bases les valeurs nominales inscrites sur la plaque signalétique de la machine.
À partir de ces bases on peut facilement déterminer la valeur de base du courant, du couple et de la résistance.
L'exemple suivant montre la façon de procéder.
Exemple 1-20
La plaque signalétique d'un moteur à courant continu donne l'information suivante :
Puissance: 30 kW
Tension: 240 V
Vitesse: 1200 r/min
Résistance du champ shunt: 42Ω
a) Calculer la valeur de base de la résistance et du couple
b) Sachant que le moteur développe un couple de 0,3 p.u. lorsqu'il tourne à une vitesse de 0.65 p.u. exprimer ces valeurs en termes réels
c) Calculer la valeur relative de la résistance du champ shunt
Solution
a) La valeur de la résistance de base est:
Rbase= Ebase / Pbase = 240² / 30 000 = 1,92Ω
La valeur du couple de base est donnée par l'équation (1-5), soit:
Tbase = 9.55 Pbase / nbase = 9,55 x 30 000 / 1200 = 239 N.m
b) Un couple de 0,3 p.u. correspond à une valeur réelle de:
Tréel = Tp.u. / Tbase = 0,3 x 239 = 71,7 N.m
Une vitesse de 0,65 p.u. correspond à une valeur réelle de:
nréel= np.u. / nbase = 0,65 X 1200 = 780 r/min
c) La valeur relative de la résistance du champ shunt est:
Rp.u. shut = Rréel / Rbase = 42Ω / 1.92Ω = 21.9 p.u.
