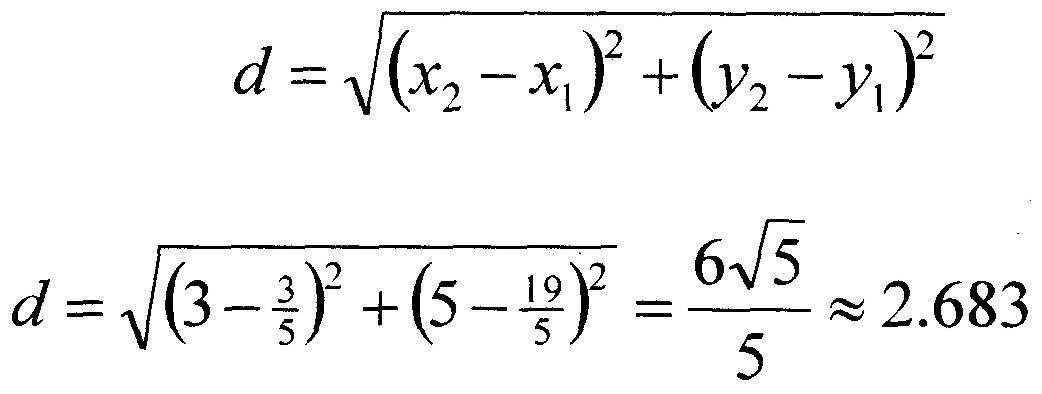
D'un point à une ligne

Les explorations mathématiques visuelles en GW-BASIC sont parfois délicates, car les coordonnées à l'écran ne correspondent pas exactement aux coordonnées cartésiennes.

Alors que le plan cartésien (ou plan de coordonnées) est divisé en quatre quadrants par l'intersection de deux axes (x et y), les graphiques à l'écran ne présentent que des paires de coordonnées supérieures ou égales à zéro. De plus, contrairement au plan de coordonnées, en GW-BASIC, pour se déplacer vers le haut à l'écran, il faut diminuer y, plutôt qu'augmenter la variable.

Supposons que nous souhaitions écrire un programme qui calcule la distance entre un point et une droite sur le plan de coordonnées ; nous voulons également que le programme trace le point et la droite à l'écran. Nous devrons non seulement coder les mathématiques de l'opération (à savoir la distance entre le point et la droite), mais aussi celles qui convertissent les coordonnées du plan cartésien en commandes graphiques GW-BASIC appropriées.

Examinons d'abord les mathématiques.

Nous souhaitons peut-être trouver la distance entre le point [3,5] et la droite 6x + 3y - 15 = 0. Transformons l'équation, qui est sous forme standard, en forme pente-ordonnée à l'origine en résolvant pour y:

y = -2x + 5

Maintenant, la distance minimale entre un point et une droite suit la trajectoire d'une droite perpendiculaire à la droite donnée.

Nous devons trouver l'équation de cette droite perpendiculaire, dont la pente est m = 1/2 (la pente inverse de la droite donnée) et qui passe par le point (3,5). Pour cela, nous utiliserons la forme point-pente, que vous connaissez peut-être en cours d'algèbre :

y - y₁ = m(x - x₁)

y - 5 = ½(x - 3)

y = ½x + 7/2

Il faut ensuite calculer le point d'intersection entre la droite donnée et la droite perpendiculaire que nous venons de trouver. En égalisant les équations des droites, en calculant x et en insérant la valeur de x dans l'une des équations pour obtenir y, nous obtenons que:

-2x + 5= ½x + 7/2

-4x + 10 = x + 7

x = 3/5

y = -2(3/5) + 5 = 19/5

Ainsi, le point d'intersection est (3/5, 19/5).

Enfin, en calculant la distance entre (3,5) et (3/5, 19/5), ce qui est facile à faire grâce à la formule de distance, nous obtenons notre réponse :

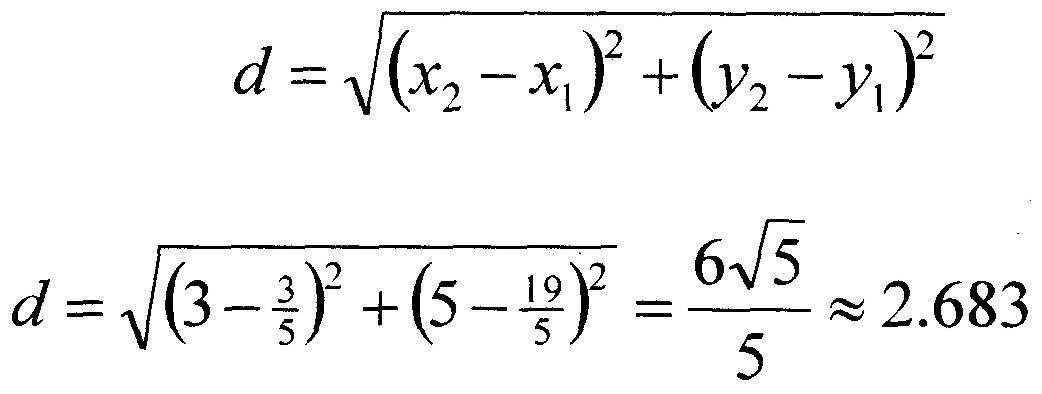
Sans surprise, il existe une formule qui parcourt toutes ces étapes en une seule. Cependant, son élaboration est un véritable casse-tête algébrique ; elle sera donc présentée ici sans démonstration.

La distance d d'un point (m, n) à une droite Ax + By + C = 0 est donnée par:

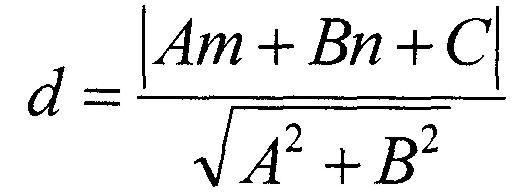
Le programme ci-dessous, COORD.BAS, calcule non seulement cette distance, mais affiche également le point et la ligne à l'écran.

Les lignes 10 à 120 interrogent l'utilisateur sur une paire de coordonnées, puis représentent ce point sur un axe de coordonnées à l'écran.

Examinez plus précisément les lignes 70 à 100 : c'est là qu'intervient la conversion entre les coordonnées cartésiennes et les coordonnées à l'écran.

Si vous trouvez ces conversions absurdes et – sachant que l'une des premières fonctions des programmes informatiques était de résoudre des problèmes mathématiques – inutiles, sachez que vous n'êtes pas seul. Les créateurs du BASIC, John Kemeny et Thomas Kurtz, partageaient ce sentiment.

Une fois le point affiché, le programme demande à l'utilisateur la pente et l'ordonnée à l'origine de la droite. Une boucle trace la droite (voir lignes 250 à 270), et une instruction INKEY$ (ligne 280) accepte la saisie au clavier, permettant ainsi d'ajuster la pente et l'ordonnée à l'origine de la droite, ainsi que la position du point, à la volée.

La distance entre le point et la droite, affichée en bas de l'écran, est mise à jour en conséquence.

Bien que le déplacement du point mette rapidement à jour le calcul de la distance, lorsque la pente ou l'ordonnée à l'origine de la droite est modifiée, vous devrez attendre qu'une nouvelle ligne apparaisse à l'écran. L'utilisation de l'instruction LINE, plutôt qu'une boucle, serait peut-être une solution plus conviviale.

COORD.BAS

10 KEY OFF:SCREEN 7:COLOR 15,0:CLS
15 PRINT"--- DISTANCE FROM A POINT TO A LINE ---"
20 INPUT"X Coordinate of point";XC
30 INPUT"Y Coordinate of point";YC
40 CLS
50 LINE(160,9)-(160,180),7
60 LINE(0,90)-(310,90),7
70 'Convert (X,Y) to (x,y)
80 '(160,90) on screen is the origin
90 XX=XC+160
100 YY=90-YC
103 LOCATE 1,1: PRINT" (";XC;",";YC;")"
104 FOR TIMES=1 TO 10
105 FOR C=1 TO 15
110 PSET(XX,YY),C
112 FOR PAUSE=1 TO 200:NEXT PAUSE
115 NEXT C
120 NEXT TIMES
200 CLS
210 INPUT"Slope";S
220 INPUT"Y-intercept";Y
221 PRINT"Use the numeric keypad to move the point"
225 PRINT"Press +/- to change slope"
226 PRINT"Press T/Y to change y-int"
227 PRINT"Press <ESC> to exit out"
228 PRINT:PRINT"Press <ENTER> to begin..."
229 INPUT T$
230 CLS
235 LINE(160,0)-(160,180),7
237 LINE(0,90)-(310,90),7
240 LOCATE 1,1:PRINT"Y=";S;"X+";Y;" (";XC;",";YC;")"
250 FOR X=-169 TO 200 STEP .1
260 PSET(X+160,90-(S*X+Y)),14
270 NEXT X
280 I$=INKEY$
281 'Calculate distance between point/line
282 DIST=ABS(-S*XC+YC-Y)/SQR((-S)^2+1)
283 LOCATE 22,1:PRINT"Distance from point to line:";DIST
284 LOCATE 1,1:PRINT"Y=";S;"X+";Y;" (";XC;",";YC;")"
285 PSET(XX,YY),15
286 FOR PAUSE=1 TO 400:NEXT PAUSE
287 PSET(XX,YY),4
290 IF I$="" THEN 280
295 PSET(XX,YY),0
300 IF I$="+" THEN S=S+.5:GOTO 230
310 IF I$="-" THEN S=S-.5:GOTO 230
320 IF I$="T" OR I$="t" THEN Y=Y-1:GOTO 230
330 IF I$="Y" OR I$="y" THEN Y=Y+1:GOTO 230
340 IF I$=CHR$(27) THEN CLS:END
341 IF I$="4" THEN XX=XX-1:XC=XC-1
342 IF I$="6" THEN XX=XX+1:XC=XC+1
343 IF I$="8" THEN YY=YY-1:YC=YC+1
344 IF I$="2" THEN YY=YY+1:YC=YC-1
350 GOTO 280