Le jeu des chiffres

GW-BASIC (PC-BASIC)

Initiation au langage Basic

Votre ordinateur comprend plusieurs fonctions mathématiques avancées. Cette section donne un aperçu des fonctions et montre comment les utiliser.

Avant de continuer, cependant, vous devez connaître quelques fonctions et définitions décrites ci-dessous.

Exponentiation

^

Rapide! Qu'est-ce que 1,5 au carré ? Que diriez-vous de 77 au cube ? Si vous ne savez pas. demander à l'ordinateur. Chaque fois que vous souhaitez élever un nombre à la puissance n, suivez ce format :

nombre (^) puissance

nombre est la base (le nombre que vous souhaitez élever à la puissance n, il peut s'agir de n'importe quelle expression numérique.

La puissance est l'exposant auquel la base est élevée. Il peut s'agir de n'importe quelle expression numérique.

Remarque : L'exponentiation a priorité sur les autres opérateurs. Par exemple, si l'ordinateur calcule - 2^2, le résultat est un nombre négatif. Pour élever - 2 à la puissance 2d "correctement" (ce qui donne un nombre positif), mettez - 2 entre parenthèses.

Commencez par 77 au cube (77^3). Après avoir regardé le bloc de syntaxe, pouvez-vous donner la commande ? Votre réponse devrait être 456533.

Si votre écran ressemble à ceci, vous êtes sur la bonne voie :

PRINT 77^3
456533
Ok 

Essayez d'élever 10 à la puissance 10. L'écran affiche :

 1E+10

Puisque 10 000 000 000 a plus de 9 chiffres significatifs, l'ordinateur est passé à la notation E.

Que diriez-vous de 100 à la puissance 100?

L'écran affiche-t-il un Overflow (débordement) ?

Overflow
1.701412E+38
Ok  

Cela signifie que la réponse est trop grande pour que l'ordinateur puisse la gérer. Tout ce qui se trouve en dehors de la plage provoque une erreur de dépassement, soit

entier 2 bytes -32768—32767

virgule flottante simple précision 4 bytes ±2.938726·10-³⁹—±1.701412·10³⁸

virgule flottante double précision 8 bytes ±2.938735877055719·10-³⁹—±1.701411834604692·10³⁸

Programme faites-le vous même

Écrivez un programme court qui affiche le carré de chaque nombre entier de 1 à 10.

5 CLS
10 FOR NUMBER = 1 TO 10
20 PRINT NUMBER^2
30 NEXT NUMBER

SQR

SQR vous permet de trouver la racine carrée d'un nombre. Voici sa syntaxe :

SQR (nombre)

nombre est zéro ou n'importe quel nombre positif.

Par exemple, si vous voulez la racine carrée de 100, tapez :

PRINT SQR(100)

et vous découvrirez (si vous ne le saviez pas déjà) que la réponse est 10.

Écrivez un autre programme court pour afficher la racine carrée de chaque dixième nombre de 100 à 0.

5 CLS
10 FOR NUMBER = 100 TO 1 STEP -10
20 PRINT SQR(NUMBER)
30 NEXT NUMBER

Fonctions trigonométriques

Regardez ce triangle. Vous l'utiliserez tout au long de la discussion sur les fonctions trigonométriques.

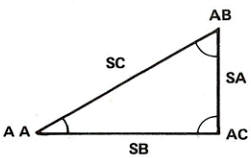
La trigonométrie a de nombreuses applications pratiques. Par exemple, imaginez que votre triangle est en fait le toit d'une maison que vous construisez. Les fonctions trigonométriques peuvent vous aider à déterminer soit la longueur des chevrons, soit la pente du toit (la « pente »). Donc, si les mathématiques vous rebutent mais que construire des choses vous excite, cette section pourrait être exactement ce que vous cherchez.

Notez que nous avons étiqueté les angles avec le préfixe A et les côtés avec le préfixe S. L'angle A, par exemple, est AA ; le côté opposé est SA.

En utilisant le triangle, nous pouvons définir les fonctions trigonométriques communes de la manière suivante :

Sinus de AA = SIN (AA) = SA/SC
Cosinus de AA = COS (AA) = SB/SC
Tangente de AA = TAN (AA) = SA/SB

Degrés vs Radians

Pour définir un angle, vous pouvez utiliser l'une des deux unités de mesure. L'unité la plus courante est le degré; l'unité "plus technique" est le radian.

Votre ordinateur suppose que tous les angles sont mesurés en radians. Étant donné que les radians peuvent vous être quelque peu étrangers, vous pouvez les convertir en degrés (et vice versa) de cette façon :

0 degré = 0 radians et 90 degré = π/2 (π/2 = 1,57)

Les exemples de programmes de ce chapitre incluent un "convertisseur" qui prend les degrés que vous avez saisis et les convertit automatiquement en radians (et vice versa dans certains cas).

SIN

Cela se prononce sinus.

Sa syntaxe est :

SIN (angle)

angle est la taille de l'angle en radians.

Étant donné la longueur d'un côté et les tailles de deux angles, vous pouvez utiliser SIN pour déterminer les longueurs des autres côtés.

Entrez et exécutez le programme suivant, en saisissant toutes les valeurs.

5 CLS
10 INPUT "QUEL EST L'ANGLE A (AA)"; AA: IF AA<=0 OR AA>=180 THEN 100
20 INPUT "QUEL EST L'ANGLE (AB)"; AB: IF AA <=0 OR AB >=180 THEN 100
30 INPUT "QUEL EST LE COTÉ (SC)"; SC: IF SC <=0 THEN 100
40 AC = 180-(AA+AB) 'VALEUR DE L'ANGLE AC
50 IF (AA+AB+AC) < > 180 THEN 100 'TRIANGLE=180 DÉGRÉES
60 AA=AA/57.29577951: AB=AB/57.29577951:AC=AC/57.29577951 'CONVERTIR DES DEGRÉS EN RADIANS
70 SA=((SIN(AA))/(SIN(AC))) * SC: IF SA<0 THEN 100
80 SB=((SIN(AB))/(SIN(AC))) * SC: IF SB<0 THEN 100
90 PRINT "COTÉ A (SA) EST " SA "DE LONG": PRINT "COTÉ (SB) EST " SB "DE LONG": GOTO 10
100 PRINT "DÉSOLÉ. CE N'EST PAS UN TRIANGLE. RÉESSAYER": GOTO 10

Lorsque l'ordinateur vous demande AB et AC. entrer les degrés des angles. Si vous entrez un nombre négatif ou un nombre supérieur ou égal à 180, l'ordinateur passe à la ligne 100. Il imprime ensuite le message et demande à nouveau les tailles.

Si vous entrez un nombre négatif pour Sc, il fait LA même chose.

Puisque vous ne connaissez pas la taille de AC, l'ordinateur la calcule automatiquement à la ligne 40. Si la somme des trois angles n'est pas égale à 180 degrés, l'ordinateur prend les mesures appropriées dans la ligne 50. La ligne 60 convertit les degrés en radians pour que l'ordinateur puisse effectuer les calculs de sinus.

Ondes sinusoïdales

Vous avez peut-être déjà vu des ondes sinusoïdales. Ils sont utilisés pour indiquer le courant alternatif et d'autres conditions électriques. Exécutez le programme suivant pour voir une onde sinusoïdale "à défilement horizontal"

1 '*** Onde sinusoïdale ***
10 CLS
15 SCREEN 7
20 LINE (0,86)-(255,86)
25 PI=3.141592
30 A1 =-4*PI
35 A2=4*PI
40 N=180
45 R=50
50 X= (A2-A1) /N
55 F=255/(A2-A1)
60 FOR I =A1 TO A2 STEP X
65 X=I*F
70 Y=R*SIN(I)
75 PSET ((X+140),(80+Y))
80 NEXT I
90 GOTO 90

COS

La fonction cosinus est liée à la fonction sinus et a la syntaxe est la suivante :

Cos (angle)
angle EST la taille de l'angle en radians.

Étant donné les longueurs de deux côtés sans la taille d'un angle, vous pouvez utiliser le cosinus pour déterminer la longueur du troisième côté d'un triangle, comme illustré ici :

5 CLS
10 INPUT "QUEL EST L'ANGLE C (AC)"; AC:IF AC<=0 OR AC>=180 THEN 100
20 AC=AC / 57.29577951'CONVERTIR DES DEGRÉS EN RADIANS
30 INPUT "QUEL EST LE COTÉ A (SA)"; SA:IF SA<=0 THEN 100
40 INPUT "QUEL EST LE COTÉ B (SB)"; SB:IF SB=<0 THEN 100
50 SC = ((SA^2)+(SB^2))-(2*(SA*SB*COS(AC))): IF SC<0 THEN 100
60 PRINT "COTÉ C (SC} EST " SQR(SC) "DE LONG":GOTO 10
100 PRINT "DÉSOLÉ, CE N'EST PAS UN TRIANGLE. RÉESSAYER": GOTO 10

5 CLS
10 FOR A = -180 TO 179 STEP 10
15 RD=A/57.29577951
30 CP=COS(RD)*14+16.5 'COS POSITION
40 SP=SIN(RD)*14+16.5 'SIN POSITION
50 IF SP<=CP THEN 70
60 PRINT TAB(CP); "C";TAB(SP);"S": GOTO 80
70 PRINT TAB(SP) ;"S" ;TAB(CP) ;"C"
80 NEXT A
90 GOTO 10

Programme faites-le vous même

Le cosinus peut faire des courbes par lui-même. Réécrivez le programme "Onde sinusoïdale" afin qu'il trace COS au lieu de SIN. Quelle est la différence entre les deux ?

TAN
La troisième fonction trigonométrique, TAN, permet de calculer la tangente d'un angle. Voici sa syntaxe :

TAN (angle)

angle est la taille de l'angle en radians.

Vous pouvez utiliser TAN pour déterminer, entre autres, un côté d'un triangle, étant donné un autre côté et un angle.

Entrez et exécutez ce programme :

5 CLS
10 INPUT "QUEL EST LE COTÉ B (SB)"; SB:IF SB<=0 THEN 100
20 INPUT "QUEL EST L'ANGLE A (AA)"; AA:IF AA<=0 OR AA>=180 THEN 100
30 AA=AA/57.28577851 'CONVERTIR DES DEGRÉS EN RADIANS
40 SA=SB*(TAN(AA)): IF SA<=0 THEN 100
50 PRINT "COTÉ A (SA) EST " SA "DE LONG":GOTO 10
100 PRINT "DÉSOLÉ, CE N'EST PAS UN TRIANGLE. RÉESSAYER": GOTO 10

La clé de ce programme, bien sûr, est la ligne 40, où la tangente de AA est multipliée par la longueur de SB pour déterminer la longueur de SA.

ATN

ATN (arc tangente) est l'inverse de TAN et a la syntaxe suivante :

ATN (angle)
angle est la taille de l'angle en radians.

Le programme suivant utilise ATN et TAN pour calculer deux angles inconnus d'un triangle lorsque deux côtés et un angle sont connus.

10 CLS
20 INPUT "QUEL EST LE COTÉ A (SA)"; SA:IF SA<=0 THEN 150
30 INPUT "QUEL EST LE COTÉ C (SC)"; SC:IF SC<=0 THEN 150
40 INPUT "QUEL EST L'ANGLE B (AB)"; AB:IF AB<=0 OR AB>=180 THEN 150
50 X=(180-AB) 'AA+AC=180-AB
60 X=X/57.28577851 'CONVERTIR DES DEGRÉS EN RADIANS
70 Y=((SA-SC)/(SA+SC))*TAN(X/2)
80 Z=ATN(Y)
90 AA=(X/2)+(Z)
100 AC=(X/2)-(Z)
110 AA=AA*57.29577951 'CONVERTIR DES DEGRÉS EN RADIANS
120 AC=AC*57.29577951 'CONVERTIR DES DEGRÉS EN RADIANS
130 PRINT "ANGLE A (AA) EST " AA "DÉGRÉES"
140 PRINT "ANGLE C (AC) EST " AC "DÉGRÉES":GOTO 20
150 PRINT "DÉSOLÉ, CE N'EST PAS UN TRIANGLE. RÉESSAYER": GOTO 20

TAN ((AA-AC)/2) est égal à ((SA-SC)/(SA + SO) * TAN ((AA + ACl/2). Notez également qu'il a fallu convertir les radians "de l'ordinateur" en "vos" degrés (Lignes 110 et 120).

LOG

LOG renvoie le logarithme naturel d'un nombre. C'est l'inverse de EXP, donc X = LOC(EXP(X)). Voici la syntaxe de LaC :

LOG (nombre)
nombre est supérieur à zéro.

Le logarithme d'un nombre est la puissance à laquelle une "base" donnée doit être élevée pour obtenir le résultat du nombre.

Les "LOG" sont utiles dans les problèmes scientifiques et mathématiques. Dans la fonction LOG, si vous omettez la base, l'ordinateur suppose que vous spécifiez Base e (2.718281828).

Pour trouver le logarithme d'un nombre 10 d'une autre base, B. utilisez cette formule :

LOG base B (x) = LOG e (x) / LOG e (B)

Par exemple. LOG (32768)/LOG(2) renvoie le logarithme 10 Base 2 de 32768. (Il renvoie la puissance à laquelle 2 est élevé pour obtenir 32768.)

Essayez ceux-ci :

PRINT LOG(1)
PRINT LOG (100)
PRINT LOG (2.718281828)

Calculez le LOG de chacun des nombres suivants :
a) 1003 b) 74,9865 c) 3,354285

a.) ?LOG (1003)
6.910751

b.) ?LOG(74.8865)
4.315974

c,) ? LOG(3.354285)
1.210239

Calculez le log à Base de chacun des nombres suivants :

a) 1 b)10 c) 100
d) 500 e) 0.1 f) 1001
log e x
Hint: log 10 x =
log e 10

5 CLS
10 INPUT "QUEL NOMBRE "; NUMBER
15 X=LOG(NUMBER)/LOG(10)
20 PRINT "LE LOG BASE 10 DE" NUMBER "EST" X
25 GOTO 10

a.) 0

Remarque : Le log de 1 dans n'importe quelle base est 0.

b.) 1
c.) 2
d.) 2.69897
e.) - 1
f.) 3.000435

EXP

La fonction EXP renvoie l'exponentielle naturelle d'un nombre (enombre).

EXP est l'inverse de LOG ; donc X = EXP(LOG(X)). Voici la syntaxe d'EXP :

EXP (nombre)
nombre est inférieur à 87,3365.

Exécutez ce programme pour voir EXP au travail.

10 CLS
20 INPUT "ENTREZ X"; X
30 PRINT "EXP(X)=" ; EXP(X)
40 GOTO 20

FIX

C'est impressionnant quand votre ordinateur porte un nombre jusqu'à 9 chiffres significatifs, surtout quand 8 de ces nombres sont à droite de la virgule décimale.

Cependant, parfois, vous ne voudrez peut-être pas tous ces chiffres ; vous ne voudrez peut-être que la partie entière (le nombre à gauche de la virgule décimale).

FIX vous permet de geler ce nombre entier en coupant simplement tous les chiffres à droite de la virgule décimale. Voici la syntaxe de FIX :

FIX (nombre)

Par exemple, tapez :

PRINT FIX (2.26413851)

Le résultat est
2
Ok 

Voici un programme qui décompose un nombre en ses parties entières et fractionnaires.

10 CLS
20 INPUT"UN NOMBRE COMME X.YZ" ; X
30 W=FIX(X)
40 F=ABS (X) -ABS (W)
50 PRINT"LA PARTIE ENTIERE EST ";W
60 PRINT"LA PARTIE FRACTIONNELLE EST "; F
70 GOTO 20

INT

Pour tronquer une expression à un nombre entier.

Syntaxe:
INT(x)

Les nombres négatifs renvoient le nombre le plus bas suivant.

Les fonctions FIX et CINT renvoient également des valeurs entières.

Exemples:

PRINT INT(98. 89)
98

PRINT INT(-12. 11)
-13

SGN

Pour retourner le signe de x.

Syntaxe:

SGN(x)

x est une expression numérique quelconque.

Si x est positif, SGN(x) renvoie 1.

Si x vaut 0, SGN(x) renvoie 0.

Si x est négatif, SGN(x) renvoie -1.

Cette instruction est similaire, mais pas la même que SIN(x), qui renvoie une fonction trigonométrique en radians, plutôt qu'en uns et zéros.

Exemples:

10 INPUT "Entrez une valeur", x
20 ON SGN(X)+2 GOTO 100, 200, 300

GW-BASIC passe à 100 si X est négatif, 200 si X est 0 et 300 si X est positif.

DEF FN

GW-BASIC a une fonction numérique, DEF FN, qui ne ressemble à aucune autre dont nous avons parlé jusqu'à présent. DEF FN vous permet de créer votre propre fonction mathématique.

Vous pouvez utiliser votre nouvelle fonction de la même manière que n'importe quelle fonction disponible (SIN, COS, TAN, etc.). Une fois que vous avez utilisé DEF FN pour définir une fonction, vous pouvez la mettre en œuvre dans votre programme en attachant le préfixe FN au nom que vous attribuez à la nouvelle fonction.

Voici la syntaxe pour DEF FN :

DEF FN nom (liste de variables) - le nom de la formule est le nom que vous attribuez à la fonction que vous créez.

La liste des variables contient une "variable factice" pour chaque variable à utiliser par la fonction.

La formule définit l'opération sur les termes des variables données dans la liste des variables.

Remarque : Les noms de variable qui apparaissent dans la formule servent uniquement à définir la formule ; elles n'affectent pas les variables de programme portant le même nom. Vous ne pouvez avoir qu'un seul argument dans un appel de formule, par conséquent, DEF FN ne doit contenir qu'une seule variable.

Vous ne pouvez utiliser DEF FN que dans un programme, pas dans le mode l'immédiat.

Par exemple, une opération mathématique que vous avez dû utiliser plusieurs fois dans cette ection est la conversion degré-radian. Ne serait-il pas agréable que l'ordinateur le fasse pour vous ?

Si vous modifiez l'exemple de programme que nous avons utilisé pour ATAN, vous verrez comment créer un DEF FN qui convertit les degrés en radians.

7 DEF FNR(X)=X/57.29577951
60 X=FNR(X):
110 AA=FNR(AA): AC=FNR(AC)

Effacez la ligne 120.

7 DEF FNR(X)=X/57.29577951
10 CLS
20 INPUT "QUEL EST LE COTÉ A (SA)"; SA:IF SA<=0 THEN 150
30 INPUT "QUEL EST LE COTÉ C (SC)"; SC:IF SC<=0 THEN 150
40 INPUT "QUEL EST L'ANGLE B (AB)"; AB:IF AB<=0 OR AB>=180 THEN 150
50 X=(180-AB) 'AA+AC=180-AB
60 X=FNR(X):
70 Y=((SA-SC)/(SA+SC))*TAN(X/2)
80 Z=ATN(Y)
90 AA=(X/2)+(Z)
100 AC=(X/2)-(Z)
110 AA=FNR(AA): AC=FNR(AC)
130 PRINT "ANGLE A (AA) EST " AA "DÉGRÉES"
140 PRINT "ANGLE C (AC) EST " AC "DÉGRÉES":GOTO 20
150 PRINT "DÉSOLÉ, CE N'EST PAS UN TRIANGLE. RÉESSAYER": GOTO 20

Vous pouvez voir tout de suite combien cela économise en tapant, puisque vous n'avez dû entrer 57.29577951 qu'une seule fois. Chaque fois que FNR est appelé en cours d'utilisation, l'ordinateur insère automatiquement les valeurs que vous avez utilisées et effectue l'opération prescrite.

Programme faites-le vous même

Utilisez DEF FN pour :

1. Convertissez les radians en degrés.
2. Créez une fonction mathématique qui décompose les nombres.

1. ) DEFFNR (X) = X*57. 28577851

2. )

5 CLS
10 DEF FNC(X) = X^3
20 INPUT "QUEL NOMBRE VOULEZ-VOUS METTRE AU CUBE ";X
30 X=FNC(X)
40 PRINT X
50 FOR A = 1 TO 75
55 NEXT A
610 GOTO 20

Voici un résumé des fonctions trigonométriques

Veuillez noter que les informations ci-dessus peuvent ne pas être exhaustives.

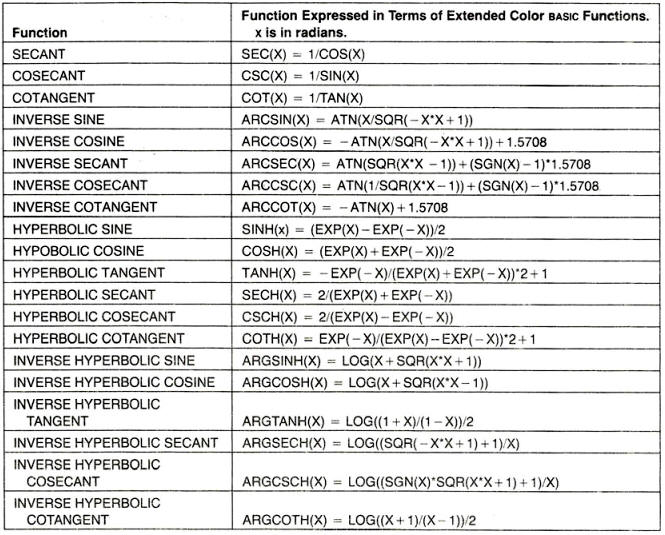
Certaines valeurs spéciales sont mathématiquement indéfinies, mais nos fonctions peuvent fournir des valeurs non valides :

TAN et SEC de 90 et 270 degrés
COT et SCS de 0 et 180 degrés

Les autres valeurs qui ne sont pas disponibles de ces fonctions sont :

ARCSIN(-1) = -PI/2
ARCSIN( 1) = PI/2
ARCCOS(-1) = PI
ARCCOS( 1) = 0
ARCSEC(-1) = -PI
ARCSEC( 1) = 0
ARCCSC(-1) = -PI/2
ARCCSC( 1) = PI/2