Python, Classes et interfaces graphiques

Python

La programmation orientée objet convient particulièrement bien au développement d’applications avec interface graphique. Des bibliothèques de classes comme tkinter ou wxPython fournissent une base de widgets très étoffée, que nous pouvons adapter à nos besoins par dérivation.

Dans cette section, nous allons utiliser à nouveau la bibliothèque tkinter, mais en appliquant les concepts décrits dans les pages précédentes, et en nous efforçant de mettre en évidence les avantages qu’apporte l’orientation objet dans nos programmes.

Code des couleurs : un petit projet bien encapsulé

Nous allons commencer par un petit projet qui nous a été inspiré par le cours d’initiation à l’électronique. L’application que nous décrivons ci-après permet de retrouver rapidement le code de trois couleurs qui correspond à une résistance électrique de valeur bien déterminée.

Pour rappel, la fonction des résistances électriques consiste à s’opposer (à résister) plus ou moins bien au passage du courant. Les résistances se présentent concrètement sous la forme de petites pièces tubulaires cerclées de bandes de couleur (en général 3). Ces bandes de couleur indiquent la valeur numérique de la résistance, en fonction du code suivant :

Chaque couleur correspond conventionnellement à l’un des chiffres de zéro à neuf :

Noir = 0 ; Brun = 1 ; Rouge = 2 ; Orange = 3 ; Jaune = 4 ;
Vert = 5 ; Bleu = 6 ; Violet = 7 ; Gris = 8 ; Blanc = 9.

On oriente la résistance de manière telle que les bandes colorées soient placées à gauche. La valeur de la résistance – exprimée en ohms (Ω) – s’obtient en lisant ces bandes colorées également à partir de la gauche :

les deux premières bandes indiquent les deux premiers chiffres de la valeur numérique; il faut ensuite accoler à ces deux chiffres un nombre de zéros égal à l’indication fournie par la troisième bande.

Exemple concret :

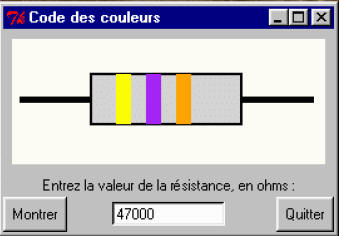
supposons qu’à partir de la gauche, les bandes colorées soient jaune, violette et verte. La valeur de cette résistance est 4700000 Ω, ou 4700 kΩ, ou encore 4,7 MΩ.

Ce système ne permet évidemment de préciser une valeur numérique qu’avec deux chiffres significatifs seulement. Il est toutefois considéré comme largement suffisant pour la plupart des applications électroniques « ordinaires » (radio, TV, etc.).

Cahier des charges de notre programme

Notre application doit faire apparaître une fenêtre comportant un dessin de la résistance, ainsi qu’un champ d’entrée dans lequel l’utilisateur peut encoder une valeur numérique. Un bouton <Montrer> déclenche la modification du dessin de la résistance, de telle façon que les trois bandes de couleur se mettent en accord avec la valeur numérique introduite.

Contrainte : Le programme doit accepter toute entrée numérique fournie sous forme entière ou réelle, dans les limites de 10 à 1011 Ω.

Par exemple, une valeur telle que 4.78e6 doit être acceptée et arrondie correctement, c’est-à-dire convertie en 4800000 Ω.

Mise en œuvre concrète

Nous construisons le corps de cette application simple sous la forme d’une classe. Nous voulons vous montrer ainsi comment une classe peut servir d’espace de noms commun, dans lequel vous pouvez encapsuler vos variables et nos fonctions. Le principal intérêt de procéder ainsi est que cela vous permet de vous passer de variables globales.

En effet :

• Mettre en route l’application se résumera à instancier un objet de cette classe.

• Les fonctions que l’on voudra y mettre en œuvre seront les méthodes de cet objet-application.

• À l’intérieur de ces méthodes, il suffira de rattacher un nom de variable au paramètre self pour que cette variable soit accessible de partout à l’intérieur de l’objet. Une telle variable d’instance est donc tout à fait l’équivalent d’une variable globale (mais seulement à l’intérieur de l’objet), puisque toutes les autres méthodes de cet objet peuvent y accéder par l’intermédiaire de self.

1# class Application(object):
2#     def __init__(self):
3#         """Constructeur de la fenêtre principale"""
4#         self.root =Tk()
5#         self.root.title('Code des couleurs')
6#         self.dessineResistance()
7#         Label(self.root, text ="Entrez la valeur de la résistance, en ohms :").\
8#         grid(row =2, column =1, columnspan =3)
9#         Button(self.root, text ='Montrer', command =self.changeCouleurs).\
10#        grid(row =3, column =1)
11#        Button(self.root, text ='Quitter', command =self.root.quit).\
12#        grid(row =3, column =3)
13#        self.entree = Entry(self.root, width =14)
14#        self.entree.grid(row =3, column =2)
15#        # Code des couleurs pour les valeurs de zéro à neuf :
16#        self.cc = ['black','brown','red','orange','yellow',
17#        'green','blue','purple','grey','white']
18#        self.root.mainloop()
19#
20#     def dessineResistance(self):
21#         """Canevas avec un modèle de résistance à trois lignes colorées"""
22#         self.can = Canvas(self.root, width=250, height =100, bg ='ivory')
23#         self.can.grid(row =1, column =1, columnspan =3, pady =5, padx =5)
24#         self.can.create_line(10, 50, 240, 50, width =5) # fils
25#         self.can.create_rectangle(65, 30, 185, 70, fill ='light grey', width =2)
26#         # Dessin des trois lignes colorées (noires au départ) :
27#         self.ligne =[] # on mémorisera les trois lignes dans 1 liste
28#         for x in range(85,150,24):
29#         self.ligne.append(self.can.create_rectangle(x,30,x+12,70,
30#         fill='black',width=0))
31#
32#     def changeCouleurs(self):
33#         """Affichage des couleurs correspondant à la valeur entrée"""
34#         self.v1ch = self.entree.get() # cette méthode renvoie une chaîne
35#         try:
36#             v = float(self.v1ch) # conversion en valeur numérique
37#         except:
38#             err =1 # erreur : entrée non numérique
39#         else:
40#             err =0
41#         if err ==1 or v < 10 or v > 1e11 :
42#             self.signaleErreur() # entrée incorrecte ou hors limites
43#         else:
44#             li =[0]*3 # liste des 3 codes à afficher
45#             logv = int(log10(v)) # partie entière du logarithme
46#             ordgr = 10**logv # ordre de grandeur
47#             # extraction du premier chiffre significatif :
48#             li[0] = int(v/ordgr) # partie entière
49#             decim = v/ordgr - li[0] # partie décimale
50#             # extraction du second chiffre significatif :
51#             li[1] = int(decim*10 +.5) # +.5 pour arrondir correctement
52#             # nombre de zéros à accoler aux 2 chiffres significatifs :
53#             li[2] = logv -1
54#             # Coloration des 3 lignes :
55#             for n in range(3):
56#                 self.can.itemconfigure(self.ligne[n], fill =self.cc[li[n]])
57#
58#     def signaleErreur(self):
59#         self.entree.configure(bg ='red') # colorer le fond du champ
60#         self.root.after(1000, self.videEntree) # après 1 seconde, effacer
61#
62#     def videEntree(self):
63#         self.entree.configure(bg ='white') # rétablir le fond blanc
64#         self.entree.delete(0, len(self.v1ch)) # enlever les car. présents
65#
66# # Programme principal :
67# if __name__ == '__main__':
68#     from tkinter import *
69#     from math import log10 # logarithmes en base 10
70#     f = Application() # instanciation de l'objet application

Commentaires

• Ligne 1 : La classe est définie comme une nouvelle classe indépendante (elle ne dérive d’aucune classe parente préexistante, mais seulement de object, « ancêtre » de toutes les classes).

• Lignes 2 à 14 : Le constructeur de la classe instancie les widgets nécessaires : espace graphique, libellés et boutons. Afin d’améliorer la lisibilité du programme, cependant, nous avons placé l’instanciation du canevas (avec le dessin de la résistance) dans une méthode distincte : dessineResistance(). Veuillez remarquer aussi que pour obtenir un code plus compact, nous ne mémorisons pas les boutons et le libellé dans des variables, parce que nous ne souhaitons pas y faire référence ailleurs dans le programme. Le positionnement des widgets dans la fenêtre utilise la méthode grid().

• Lignes 15-17 : Le code des couleurs est mémorisé dans une simple liste.

• Ligne 18 : La dernière instruction du constructeur démarre l’application. Si vous préférez démarrer l’application indépendamment de sa création, vous devez supprimer cette ligne, et reporter l’appel à mainloop() au niveau principal du programme, en ajoutant une instruction : f.root.mainloop() à la ligne 71.

• Lignes 20 à 30 : Le dessin de la résistance se compose d’une ligne et d’un premier rectangle gris clair, pour le corps de la résistance et ses deux fils. Trois autres rectangles figureront les bandes colorées que le programme devra modifier en fonction des entrées de l’utilisateur. Ces bandes sont noires au départ ; elles sont référencées dans la liste self.ligne.

• Lignes 32 à 53 : Ces lignes contiennent l’essentiel de la fonctionnalité du programme. L’entrée brute fournie par l’utilisateur est acceptée sous la forme d’une chaîne de caractères. À la ligne 36, on essaie de convertir cette chaîne en une valeur numérique de type float. Si la conversion échoue, on mémorise l’erreur. Si l’on dispose bien d’une valeur numérique, on vérifie ensuite qu’elle se situe effectivement dans l’intervalle autorisé (de 10 Ω à 1011 Ω). Si une erreur est détectée, on signale à l’utilisateur que son entrée est incorrecte en colorant de rouge le fond du champ d’entrée, qui est ensuite vidé de son contenu (lignes 55 à 61).

• Lignes 45-46 : Les mathématiques viennent à notre secours pour extraire de la valeur numérique son ordre de grandeur (c’est-à-dire l’exposant de 10 le plus proche). Veuillez consulter un ouvrage de mathématiques pour de plus amples explications concernant les logarithmes.

• Lignes 47-48 : Une fois connu l’ordre de grandeur, il devient relativement facile d’extraire du nombre traité ses deux premiers chiffres significatifs. Exemple : supposons que la valeur entrée soit 31687. Le logarithme de ce nombre est 4,50088... dont la partie entière (4) nous donne l’ordre de grandeur de la valeur entrée (soit 104). Pour extraire de celle-ci son premier chiffre significatif, il suffit de la diviser par 104, soit 10000, et de conserver seulement la partie entière du résultat (3).

• Lignes 49 à 51 : Le résultat de la division effectuée dans le paragraphe précédent est 3,1687. Nous récupérons la partie décimale de ce nombre à la ligne 49, soit 0,1687 dans notre exemple. Si nous le multiplions par dix, ce nouveau résultat comporte une partie entière qui n’est rien d’autre que notre second chiffre significatif (1 dans notre exemple). Nous pourrions facilement extraire ce dernier chiffre, mais puisque c’est le dernier, nous souhaitons encore qu’il soit correctement arrondi. Pour ce faire, il suffit d’ajouter une demi unité au produit de la multiplication par dix, avant d’en extraire la valeur entière. Dans notre exemple, en effet, ce calcul donnera donc 1,687 + 0,5 = 2,187 , dont la partie entière (2) est bien la valeur arrondie recherchée.

• Ligne 53 : Le nombre de zéros à accoler aux deux chiffres significatifs correspond au calcul de l’ordre de grandeur. Il suffit de retirer une unité au logarithme.

• Ligne 56 : Pour attribuer une nouvelle couleur à un objet déjà dessiné dans un canevas, on utilise la méthode itemconfigure(). Nous utilisons donc cette méthode pour modifier l’option fill de chacune des bandes colorées, en utilisant les noms de couleur extraits de la liste self.cc grâce à aux trois indices li[1], li[2] et li[3] qui contiennent les 3 chiffres correspondants.

La solution des exercices se trouve à la fin

Exercices

13.1 Modifiez le script ci-dessus de telle manière que le fond d’image devienne bleu clair (light blue), que le corps de la résistance devienne beige (beige), que le fil de cette résistance soit plus fin, et que les bandes colorées indiquant la valeur soient plus larges.

13.2 Modifiez le script ci-dessus de telle manière que l’image dessinée soit deux fois plus grande.

13.3 Modifiez le script ci-dessus de telle manière qu’il devienne possible d’entrer aussi des valeurs de résistances comprises entre 1 et 10 Ω. Pour ces valeurs, le premier anneau coloré devra rester noir, les deux autres indiqueront la valeur en Ω et dixièmes d’Ω.

13.4 Modifiez le script ci-dessus de telle façon que le bouton <Montrer> ne soit plus nécessaire. Dans votre script modifié, il suffira de frapper <Enter> après avoir entré la valeur de la résistance, pour que l’affichage s’active.

13.5 Modifiez le script ci-dessus de telle manière que les trois bandes colorées redeviennent noires dans les cas où l’utilisateur fournit une entrée inacceptable.

Petit train : héritage, échange d’informations entre objets

Dans l’exercice précédent, nous n’avons exploité qu’une seule caractéristique des classes : l’encapsulation.

Celle-ci nous a permis d’écrire un programme dans lequel les différentes fonctions (qui sont donc devenues des méthodes) peuvent chacune accéder à un même pool de variables : toutes celles qui sont définies comme étant attachées à self.

Toutes ces variables peuvent être considérées en quelque sorte comme des variables globales à l’intérieur de l’objet. Comprenez bien toutefois qu’il ne s’agit pas de véritables variables globales. Elles restent en effet strictement confinées à l’intérieur de l’objet, et il est déconseillé de vouloir y accéder de l’extérieur.

D’autre part, tous les objets que vous instancierez à partir d’une même classe possèderont chacun leur propre jeu de ces variables, qui sont donc bel et bien encapsulées dans ces objets.

On les appelle pour cette raison des attributs d’instance. Nous allons à présent passer à la vitesse supérieure, et réaliser une petite application sur la base de plusieurs classes, afin d’examiner comment différents objets peuvent s’échanger des informations par l’intermédiaire de leurs méthodes.

Nous allons également profiter de cet exercice pour vous montrer comment vous pouvez définir la classe principale de votre application graphique par dérivation d’une classe tkinter préexistante, mettant ainsi à profit le mécanisme d’héritage.

Le projet développé ici est très simple, mais il pourrait constituer une première étape dans la réalisation d’un logiciel de jeu : nous en fournissons d’ailleurs des exemples plus loin. Il s’agit d’une fenêtre contenant un canevas et deux boutons. Lorsque l’on actionne le premier de ces deux boutons, un petit train apparaît dans le canevas. Lorsque l’on actionne le second bouton, quelques petits personnages apparaissent à certaines fenêtres des wagons.

Cahier des charges

L’application comportera deux classes :

• La classe Application() sera obtenue par dérivation d’une des classes de base de tkinter : elle mettra en place la fenêtre principale, son canevas et ses deux boutons.

• Une classe Wagon(), indépendante, permettra d’instancier dans le canevas 4 objets-wagons similaires, dotés chacun d’une méthode perso(). Celle-ci sera destinée à provoquer l’apparition d’un petit personnage à l’une quelconque des trois fenêtres du wagon. L’application principale invoquera cette méthode différemment pour différents objets-wagons, afin de faire apparaître un choix de quelques personnages.

Implémentation

1# from tkinter import *
2#
3# def cercle(can, x, y, r):
4#     "dessin d'un cercle de rayon <r> en <x,y> dans le canevas <can>"
5#     can.create_oval(x-r, y-r, x+r, y+r)
6#
7# class Application(Tk):
8#     def __init__(self):
9#          Tk.__init__(self) # constructeur de la classe parente
10#         self.can =Canvas(self, width =475, height =130, bg ="white")
11#         self.can.pack(side =TOP, padx =5, pady =5)
12#         Button(self, text ="Train", command =self.dessine).pack(side =LEFT)
13#         Button(self, text ="Hello", command =self.coucou).pack(side =LEFT)
14#
15#     def dessine(self):
16#         "instanciation de 4 wagons dans le canevas"
17#         self.w1 = Wagon(self.can, 10, 30)
18#         self.w2 = Wagon(self.can, 130, 30)
19#         self.w3 = Wagon(self.can, 250, 30)
20#         self.w4 = Wagon(self.can, 370, 30)
21#
22#     def coucou(self):
23#         "apparition de personnages dans certaines fenêtres"
24#         self.w1.perso(3) # 1er wagon, 3e fenêtre
25#         self.w3.perso(1) # 3e wagon, 1e fenêtre
26#         self.w3.perso(2) # 3e wagon, 2e fenêtre
27#         self.w4.perso(1) # 4e wagon, 1e fenêtre
28#
29# class Wagon(object):
30#     def __init__(self, canev, x, y):
31#         "dessin d'un petit wagon en <x,y> dans le canevas <canev>"
32#         # mémorisation des paramètres dans des variables d'instance :
33#         self.canev, self.x, self.y = canev, x, y
34#         # rectangle de base : 95x60 pixels :
35#         canev.create_rectangle(x, y, x+95, y+60)
36#         # 3 fenêtres de 25x40 pixels, écartées de 5 pixels :
37#         for xf in range(x+5, x+90, 30):
38#             canev.create_rectangle(xf, y+5, xf+25, y+40)
39#             # 2 roues de rayon égal à 12 pixels :
40#             cercle(canev, x+18, y+73, 12)
41#             cercle(canev, x+77, y+73, 12)
42#
43# def perso(self, fen):
44#     "apparition d'un petit personnage à la fenêtre <fen>"
45#     # calcul des coordonnées du centre de chaque fenêtre :
46#     xf = self.x + fen*30 -12
47#     yf = self.y + 25
48#     cercle(self.canev, xf, yf, 10) # visage
49#     cercle(self.canev, xf-5, yf-3, 2) # oeil gauche
50#     cercle(self.canev, xf+5, yf-3, 2) # oeil droit
51#     cercle(self.canev, xf, yf+5, 3) # bouche
52#
53# app = Application()
54# app.mainloop()

Commentaires

• Lignes 3 à 5 : Nous projetons de dessiner une série de petits cercles. Cette petite fonction nous facilitera le travail en nous permettant de définir ces cercles à partir de leur centre et leur rayon.

• Lignes 7 à 13 : La classe principale de notre application est construite par dérivation de la classe de fenêtres Tk() importée du module tkinter. Comme nous l’avons expliqué au chapitre précédent, le constructeur d’une classe dérivée doit activer lui-même le constructeur de la classe parente, en lui transmettant la référence de l’instance comme premier argument. Les lignes 10 à 13 servent à mettre en place le canevas et les boutons.

• Lignes 15 à 20 : Ces lignes instancient les 4 objets-wagons, produits à partir de la classe correspondante. Ceci pourrait être programmé plus élégamment à l’aide d’une boucle et d’une liste, mais nous le laissons ainsi pour ne pas alourdir inutilement les explications qui suivent. Nous voulons placer nos objets-wagons dans le canevas, à des emplacements bien précis : il nous faut donc transmettre quelques informations au constructeur de ces objets : au moins la référence du canevas, ainsi que les coordonnées souhaitées. Ces considérations nous font également entrevoir que lorsque nous définirons la classe Wagon(), un peu plus loin, nous devrons associer à sa méthode constructeur un nombre égal de paramètres afin de réceptionner ces arguments.

Les objets sont des entités programmées qui s’échangent des messages et interagissent par l’intermédiaire de leurs méthodes.

• Lignes 22 à 27 : Cette méthode est invoquée lorsque l’on actionne le second bouton. Elle invoque elle-même la méthode perso() de certains objets-wagons, avec des arguments différents, afin de faire apparaître les personnages aux fenêtres indiquées. Ces quelques lignes de code vous montrent donc comment un objet peut communiquer avec un autre, en faisant appel à ses méthodes. Il s’agit-là du mécanisme central de la programmation par objets : Idéalement, la méthode coucou() devrait comporter quelques instructions complémentaires, lesquelles vérifieraient d’abord si les objets-wagons concernés existent bel et bien, avant d’autoriser l’activation d’une de leurs méthodes. Nous n’avons pas inclus ce genre de garde-fou afin que l’exemple reste aussi simple que possible, mais cela entraîne la conséquence que vous ne pouvez pas actionner le second bouton avant le premier.

• Lignes 29-30 : La classe Wagon() ne dérive d’aucune autre classe préexistante. Étant donné qu’il s’agit d’une classe d’objets graphiques, nous devons cependant munir sa méthode constructeur de paramètres, afin de recevoir la référence du canevas auquel les dessins sont destinés, ainsi que les coordonnées de départ de ces dessins. Dans vos expérimentations éventuelles autour de cet exercice, vous pourriez bien évidemment ajouter encore d’autres paramètres : taille du dessin, orientation, couleur, vitesse, etc.

• Lignes 31 à 51 : Ces instructions ne nécessitent guère de commentaires. La méthode perso() est dotée d’un paramètre qui indique celle des 3 fenêtres où il faut faire apparaître un petit personnage. Ici aussi nous n’avons pas prévu de garde-fou : vous pouvez invoquer cette méthode avec un argument égal à 4 ou 5, par exemple, ce qui produira des effets incorrects.

• Lignes 53-54 : Pour cette application, contrairement à la précédente, nous avons préféré séparer la création de l’objet app, et son démarrage par invocation de mainloop(), dans deux instructions distinctes (en guise d’exemple). Vous pourriez également condenser ces deux instructions en une seule, laquelle serait alors : Application().mainloop(), et faire ainsi l’économie d’une variable.

Exercice

13.6 Perfectionnez le script décrit ci-dessus, en ajoutant un paramètre couleur au constructeur de la classe Wagon(), lequel déterminera la couleur de la cabine du wagon. Arrangez-vous également pour que les fenêtres soient noires au départ, et les roues grises (pour réaliser ce dernier objectif, ajoutez aussi un paramètre couleur à la fonction cercle()).

À cette même classe Wagon(), ajoutez encore une méthode allumer(), qui servira à changer la couleur des 3 fenêtres (initialement noires) en jaune, afin de simuler l’allumage d’un éclairage intérieur. Ajoutez un bouton à la fenêtre principale, qui puisse déclencher cet allumage. Profitez de l’amélioration de la fonction cercle() pour teinter le visage des petits personnages en rose (pink), leurs yeux et leurs bouches en noir, et instanciez les objets-wagons avec des couleurs différentes.

13.7 Ajoutez des correctifs au programme précédent, afin que l’on puisse utiliser n’importe quel bouton dans le désordre, sans que cela ne déclenche une erreur ou un effet bizarre.

OscilloGraphe : un widget personnalisé

Le projet qui suit va nous entraîner encore un petit peu plus loin. Nous allons y construire une nouvelle classe de widget, qu’il sera possible d’intégrer dans nos projets futurs comme n’importe quel widget standard. Comme la classe principale de l’exercice précédent, cette nouvelle classe sera construite par dérivation d’une classe tkinter préexistante.

Le sujet concret de cette application nous est inspiré par le cours de physique.

Pour rappel, un mouvement vibratoire harmonique se définit comme étant la projection d’un mouvement circulaire uniforme sur une droite. Les positions successives d’un mobile qui effectue ce type de mouvement sont traditionnellement repérées par rapport à une position centrale : on les appelle alors des élongations.

L’équation qui décrit l’évolution de l’élongation d’un tel mobile au cours du temps est toujours de la forme

dans laquelle e représente l’élongation du mobile à tout instant t. Les constantes A, f et φ désignent respectivement l’amplitude, la fréquence et la phase du mouvement vibratoire. Le but du présent projet est de fournir un instrument de visualisation simple de ces différents concepts, à savoir un système d’affichage automatique de graphiques élongation/temps.

L’utilisateur pourra choisir librement les valeurs des paramètres A, f et φ, et observer les courbes qui en résultent. Le widget que nous allons construire d’abord s’occupera de l’affichage proprement dit. Nous construirons ensuite d’autres widgets pour faciliter l’entrée des paramètres A, f et φ.

Veuillez donc encoder le script ci-dessous et le sauvegarder dans un fichier, auquel vous donnerez le nom oscillo.py. Vous réaliserez ainsi un véritable module contenant une classe (vous pourrez par la suite ajouter d’autres classes dans ce même module, si le cœur vous en dit).

1# from tkinter import *
2# from math import sin, pi
3#
4# class OscilloGraphe(Canvas):
5#     "Canevas spécialisé, pour dessiner des courbes élongation/temps"
6#     def __init__(self, boss =None, larg=200, haut=150):
7#         "Constructeur du graphique : axes et échelle horiz."
8#         # construction du widget parent :
9#         Canvas.__init__(self) # appel au constructeur
10#         self.configure(width=larg, height=haut) # de la classe parente
11#         self.larg, self.haut = larg, haut # mémorisation
12#         # tracé des axes de référence :
13#         self.create_line(10, haut/2, larg, haut/2, arrow=LAST) # axe X
14#         self.create_line(10, haut-5, 10, 5, arrow=LAST) # axe Y
15#         # tracé d'une échelle avec 8 graduations :
16#         pas = (larg-25)/8. # intervalles de l'échelle horizontale
17#         for t in range(1, 9):
18#             stx = 10 + t*pas # +10 pour partir de l'origine
19#             self.create_line(stx, haut/2-4, stx, haut/2+4)
20#
21# def traceCourbe(self, freq=1, phase=0, ampl=10, coul='red'):
22#     "tracé d'un graphique élongation/temps sur 1 seconde"
23#     curve =[] # liste des coordonnées
24#     pas = (self.larg-25)/1000. # l'échelle X correspond à 1 seconde
25#     for t in range(0,1001,5): # que l'on divise en 1000 ms.
26#         e = ampl*sin(2*pi*freq*t/1000 - phase)
27#         x = 10 + t*pas
28#         y = self.haut/2 - e*self.haut/25
29#         curve.append((x,y))
30#         n = self.create_line(curve, fill=coul, smooth=1)
31#         return n # n = numéro d'ordre du tracé
32#
33# #### Code pour tester la classe : ####
34#
35# if __name__ == '__main__':
36#     root = Tk()
37#     gra = OscilloGraphe(root, 250, 180)
38#     gra.pack()
39#     gra.configure(bg ='ivory', bd =2, relief=SUNKEN)
40#     gra.traceCourbe(2, 1.2, 10, 'purple')
41#     root.mainloop()

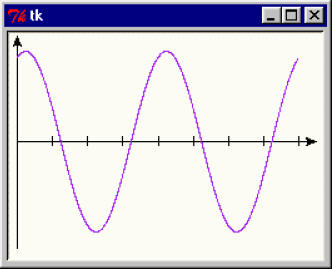
Le niveau principal du script est constitué par les lignes 35 à 41. Comme nous l’avons déjà expliqué à la page 188, les lignes de code situées après l’instruction if __name__ == '__main__': ne sont pas exécutées si le script est importé en tant que module dans une autre application. Si on lance le script comme application principale, par contre, ces instructions s’exécutent.

Nous disposons ainsi d’un mécanisme intéressant, qui nous permet d’intégrer des instructions de test à l’intérieur des modules, même si ceux-ci sont destinés à être importés dans d’autres scripts. Lancez donc l’exécution du script de la manière habituelle.

Vous devriez obtenir un affichage similaire à celui qui est reproduit à la page précédente. Expérimentation Nous commenterons les lignes importantes du script un peu plus loin dans ce texte. Mais commençons d’abord par expérimenter quelque peu la classe que nous venons de construire.

Ouvrez donc votre terminal, et entrez les instructions ci-dessous directement à la ligne de commande :

>>> from oscillo import *
>>> g1 = OscilloGraphe()
>>> g1.pack()

Après importation des classes du module oscillo, nous instancions un premier objet g1, de la classe OscilloGraphe().

Puisque nous ne fournissons aucun argument, l’objet possède les dimensions par défaut, définies dans le constructeur de la classe. Remarquons au passage que nous n’avons même pas pris la peine de définir d’abord une fenêtre maître pour y placer ensuite notre widget. tkinter nous pardonne cet oubli et nous en fournit une automatiquement !

>>> g2 = OscilloGraphe(haut=200, larg=250)
>>> g2.pack()
>>> g2.traceCourbe()

Par ces instructions, nous créons un second widget de la même classe, en précisant cette fois ses dimensions (hauteur et largeur, dans n’importe quel ordre).

Ensuite, nous activons la méthode traceCourbe() associée à ce widget. Étant donné que nous ne lui fournissons aucun argument, la sinusoïde qui apparaît correspond aux valeurs prévues par défaut pour les paramètres A, f et φ.

>>> g3 = OscilloGraphe(larg=220)
>>> g3.configure(bg='white', bd=3, relief=SUNKEN)
>>> g3.pack(padx=5,pady=5)
>>> g3.traceCourbe(phase=1.57, coul='purple')
>>> g3.traceCourbe(phase=3.14, coul='dark green')

Pour comprendre la configuration de ce troisième widget, il faut nous rappeler que la classe OscilloGraphe() a été construite par dérivation de la classe Canvas().

Elle hérite donc toutes les propriétés de celle-ci, ce qui nous permet de choisir la couleur de fond, la bordure, etc., en utilisant les mêmes arguments que ceux qui sont à notre disposition lorsque nous configurons un canevas. Nous faisons ensuite apparaître deux tracés successifs, en faisant appel deux fois à la méthode traceCourbe(), à laquelle nous fournissons des arguments pour la phase et la couleur.

Exercice

13.8 Créez un quatrième widget, de taille : 400 × 300, couleur de fond : jaune, et faites-y apparaître plusieurs courbes correspondant à des fréquences et des amplitudes différentes.

Il est temps à présent que nous analysions la structure de la classe qui nous a permis d’instancier tous ces widgets. Nous avons donc enregistré cette classe dans le module oscillo.py

Cahier des charges

Nous souhaitons définir une nouvelle classe de widget, capable d’afficher automatiquement les graphiques élongation/temps correspondant à divers mouvements vibratoires harmoniques. Ce widget doit pouvoir être dimensionné à volonté au moment de son instanciation. Il doit faire apparaître deux axes cartésiens X et Y munis de flèches.

L’axe X représentera l’écoulement du temps pendant une seconde au total, et il sera muni d’une échelle comportant 8 intervalles. Une méthode traceCourbe() sera associée à ce widget. Elle provoquera le tracé du graphique élongation/temps pour un mouvement vibratoire, dont on aura fourni la fréquence (entre 0.25 et 10 Hz), la phase (entre 0 et 2π radians) et l’amplitude (entre 1 et 10 ; échelle arbitraire).

Implémentation

• Ligne 4 : La classe OscilloGraphe() est créée par dérivation de la classe Canvas(). Elle hérite donc toutes les propriétés de celle-ci : on pourra configurer les objets de cette nouvelle classe en utilisant les nombreuses options déjà disponibles pour la classe Canvas().

• Ligne 6 : La méthode constructeur utilise 3 paramètres, qui sont tous optionnels puisque chacun d’entre eux possède une valeur par défaut. Le paramètre boss ne sert qu’à réceptionner la référence d’une fenêtre maîtresse éventuelle (voir exemples suivants). Les paramètres larg et haut (largeur et hauteur) servent à assigner des valeurs aux options width et height du canevas parent, au moment de l’instanciation.

• Lignes 9-10 : Comme nous l’avons déjà dit à plusieurs reprises, le constructeur d’une classe dérivée doit presque toujours commencer par activer le constructeur de sa classe parente. Nous ne pouvons en effet hériter toute la fonctionnalité de la classe parente, que si cette fonctionnalité a été effectivement mise en place et initialisée. Nous activons donc le constructeur de la classe Canvas() à la ligne 9, et nous ajustons deux de ses options à la ligne 10. Notez au passage que nous pourrions condenser ces deux lignes en une seule, qui deviendrait en l’occurrence : Canvas.__init__(self, width=larg, height=haut). Et comme cela a également déjà été expliqué, nous devons transmettre à ce constructeur la référence de l’instance présente (self) comme premier argument.

• Ligne 11 : Il est nécessaire de mémoriser les paramètres larg et haut dans des variables d’instance, parce que nous devrons pouvoir y accéder aussi dans la méthode traceCourbe().

• Lignes 13-14 : Pour tracer les axes X et Y, nous utilisons les paramètres larg et haut, ainsi ces axes sont automatiquement mis à dimension. L’option arrow=LAST permet de faire apparaître une petite flèche à l’extrémité de chaque ligne.

• Lignes 16 à 19 : Pour tracer l’échelle horizontale, on commence par réduire de 25 pixels la largeur disponible, de manière à ménager des espaces aux deux extrémités. On divise ensuite en 8 intervalles, que l’on visualise sous la forme de 8 petits traits verticaux.

• Ligne 21 : La méthode traceCourbe() pourra être invoquée avec quatre arguments. Chacun d’entre eux pourra éventuellement être omis, puisque chacun des paramètres correspondants possède une valeur par défaut. Il sera également possible de fournir les arguments dans n’importe quel ordre, comme nous l’avons déjà expliqué.

• Lignes 23 à 31 : Pour le tracé de la courbe, la variable t prend successivement toutes les valeurs de 0 à 1000, et on calcule à chaque fois l’élongation e correspondante, à l’aide de la formule théorique (ligne 26). Les couples de valeurs t et e ainsi trouvées sont mises à l’échelle et transformées en coordonnées x, y aux lignes 27 et 28, puis accumulées dans la liste curve.

• Lignes 30-31 : La méthode create_line() trace alors la courbe correspondante en une seule opération, et elle renvoie le numéro d’ordre du nouvel objet ainsi instancié dans le canevas (ce numéro d’ordre nous permettra d’y accéder encore par après : pour l’effacer, par exemple). L’option smooth =1 améliore l’aspect final, par lissage.

Exercices

13.9 Modifiez le script de manière à ce que l’axe de référence vertical comporte lui aussi une échelle, avec 5 tirets de part et d’autre de l’origine.

13.10 Comme les widgets de la classe Canvas() dont il dérive, votre widget peut intégrer des indications textuelles. Il suffit pour cela d’utiliser la méthode create_text(). Cette méthode attend au moins trois arguments : les coordonnées x et y de l’emplacement où vous voulez faire apparaître votre texte et puis le texte lui-même, bien entendu. D’autres arguments peuvent être transmis sous forme d’options, pour préciser par exemple la police de caractères et sa taille.

Afin de voir comment cela fonctionne, ajoutez provisoirement la ligne suivante dans le constructeur de la classe OscilloGraphe(), puis relancez le script :

self.create_text(130, 30, text = "Essai", anchor =CENTER)

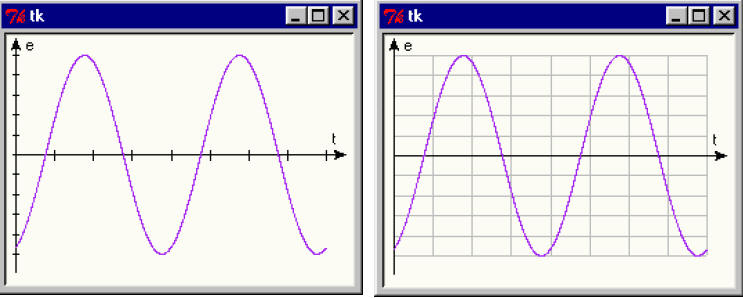
Utilisez cette méthode pour ajouter au widget les indications suivantes aux extrémités des axes de référence : e (pour « élongation ») le long de l’axe vertical, et t (pour « temps ») le long de l’axe horizontal. Le résultat pourrait ressembler à la figure de gauche.

13.11 Vous pouvez compléter encore votre widget en y faisant apparaître une grille de référence plutôt que de simples tirets le long des axes. Pour éviter que cette grille ne soit trop visible, vous pouvez colorer ses traits en gris (option fill = ’grey’), comme dans la figure de droite.

13.12 Complétez encore votre widget en y faisant apparaître des repères numériques.

Curseurs : un widget composite

Dans l’exercice précédent, vous avez construit un nouveau type de widget que vous avez sauvegardé dans le module oscillo.py. Conservez soigneusement ce module, car vous l’intégrerez bientôt dans un projet plus complexe. Pour l’instant, vous allez construire un autre widget, plus interactif cette fois. Il s’agira d’une sorte de panneau de contrôle comportant trois curseurs de réglage et une case à cocher. Comme le précédent, ce widget est destiné à être réutilisé dans une application de synthèse.

Présentation du widget Scale

Commençons d’abord par découvrir un widget de base, que nous n’avions pas encore utilisé jusqu’ici : le widget Scale se présente comme un curseur qui coulisse devant une échelle. Il permet à l’utilisateur de choisir rapidement la valeur d’un paramètre quelconque, d’une manière très attrayante.

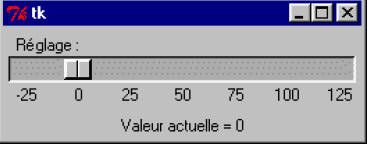
Le petit script ci-dessous vous montre comment le paramétrer et l’utiliser dans une fenêtre :

from tkinter import *
def updateLabel(x):
    lab.configure(text='Valeur actuelle = ' + str(x))

root = Tk()
Scale(root, length=250, orient=HORIZONTAL, label ='Réglage :',
    troughcolor ='dark grey', sliderlength =20,
    showvalue =0, from_=-25, to=125, tickinterval =25,
    command=updateLabel).pack()

lab = Label(root)
lab.pack()

root.mainloop()

Ces lignes ne nécessitent guère de commentaires. Vous pouvez créer des widgets Scale de n’importe quelle taille (option length), en orientation horizontale (comme dans notre exemple) ou verticale (option orient = VERTICAL). Les options from_ (attention : n’oubliez pas le caractère « souligné », lequel est nécessaire afin d’évi- ter la confusion avec le mot réservé from !) et to définissent la plage de réglage. L’intervalle entre les repères numériques est défini dans l’option tickinterval, etc.

La fonction désignée dans l’option command est appelée automatiquement chaque fois que le curseur est déplacé, et la position actuelle du curseur par rapport à l’échelle lui est transmise en argument. Il est donc très facile d’utiliser cette valeur pour effectuer un traitement quelconque. Considérez par exemple le paramètre x de la fonction updateLabel(), dans notre exemple.

Le widget Scale constitue une interface très intuitive et attrayante pour proposer différents réglages aux utilisateurs de vos programmes. Nous allons à présent l’incorporer en plusieurs exemplaires dans une nouvelle classe de widget : un panneau de contrôle destiné à choisir la fréquence, la phase et l’am- plitude pour un mouvement vibratoire, dont nous afficherons ensuite le graphique élongation/temps à l’aide du widget oscilloGraphe construit dans les pages précédentes.

Construction d’un panneau de contrôle à trois curseurs Comme le précédent, le script que nous décrivons ci-dessous est destiné à être sauvegardé dans un module, que vous nommerez cette fois curseurs.py. Les classes que vous sauvegardez ainsi seront réutilisées (par importation) dans une application de synthèse que nous décrirons un peu plus loin .

Nous attirons votre attention sur le fait que le code ci-dessous peut être raccourci de différentes manières (nous y reviendrons). Nous ne l’avons pas optimisé d’emblée, parce que cela nécessiterait d’y incorporer un concept supplémentaire (les expressions lambda), ce que nous préférons éviter pour l’ins- tant. Vous savez déjà que les lignes de code placées à la fin du script permettent de tester son fonctionnement. Vous devriez obtenir une fenêtre semblable à celle-ci :

1# from tkinter import *
2# from math import pi
3#
4# class ChoixVibra(Frame):
5#     """Curseurs pour choisir fréquence, phase & amplitude d'une vibration"""
6#     def __init__(self, boss =None, coul ='red'):
7#          Frame.__init__(self) # constructeur de la classe parente
8#          # Initialisation de quelques attributs d'instance :
9#          self.freq, self.phase, self.ampl, self.coul = 0, 0, 0, coul
10#         # Variable d'état de la case à cocher :
11#         self.chk = IntVar() # 'objet-variable' tkinter
12#         Checkbutton(self, text='Afficher', variable=self.chk,
13#         fg = self.coul, command = self.setCurve).pack(side=LEFT)
14#         # Définition des 3 widgets curseurs :
15#         Scale(self, length=150, orient=HORIZONTAL, sliderlength =25,
16#             label ='Fréquence (Hz) :', from_=1., to=9., tickinterval =2,
17#             resolution =0.25,
18#             showvalue =0, command = self.setFrequency).pack(side=LEFT)
19#         Scale(self, length=150, orient=HORIZONTAL, sliderlength =15,
20#             label ='Phase (degrés) :', from_=-180, to=180, tickinterval =90,
21#             showvalue =0, command = self.setPhase).pack(side=LEFT)
22#         Scale(self, length=150, orient=HORIZONTAL, sliderlength =25,
23#             label ='Amplitude :', from_=1, to=9, tickinterval =2,
24#             showvalue =0, command = self.setAmplitude).pack(side=LEFT)
25#
26# def setCurve(self):
27#     self.event_generate('<Control-Z>')
28#
29# def setFrequency(self, f):
30#     self.freq = float(f)
31#     self.event_generate('<Control-Z>')
32#
33# def setPhase(self, p):
34#     pp =float(p)
35#     self.phase = pp*2*pi/360 # conversion degrés -> radians
36#     self.event_generate('<Control-Z>')
37#
38# def setAmplitude(self, a):
39#     self.ampl = float(a)
40#     self.event_generate('<Control-Z>')
41#
42# #### Code pour tester la classe : ###
43#
44# if __name__ == '__main__':
45#     def afficherTout(event=None):
46#         lab.configure(text = '{0} - {1} - {2} - {3}'.\
47#             format(fra.chk.get(), fra.freq, fra.phase, fra.ampl))
48#     root = Tk()
49#     fra = ChoixVibra(root,'navy')
50#     fra.pack(side =TOP)
51#     lab = Label(root, text ='test')
52#     lab.pack()
53#     root.bind('<Control-Z>', afficherTout)
54#     root.mainloop()

Ce panneau de contrôle permettra à vos utilisateurs de régler aisément la valeur des paramètres indiqués (fréquence, phase et amplitude), lesquels pourront alors servir à commander l’affichage de graphiques élongation/temps dans un widget de la classe OscilloGraphe() construite précédemment, comme nous le montrerons dans l’application de synthèse.

Commentaires

• Ligne 6 : La méthode « constructeur » utilise un paramètre optionnel coul. Ce paramètre permettra de choisir une couleur pour le graphique soumis au contrôle du widget. Le paramètre boss sert à réceptionner la référence d’une fenêtre maîtresse éventuelle (voir plus loin).

• Ligne 7 : Activation du constructeur de la classe parente (pour hériter sa fonctionnalité).

• Ligne 9 : Déclaration de quelques variables d’instance. Leurs vraies valeurs seront déterminées par les méthodes des lignes 29 à 40 (gestionnaires d’événements).

• Ligne 11 : Cette instruction instancie un objet de la classe IntVar(), laquelle fait partie du module tkinter au même titre que les classes similaires DoubleVar(), StringVar() et BooleanVar(). Toutes ces classes permettent de définir des variables tkinter, lesquels sont en fait des objets, mais qui se comportent comme des variables à l’intérieur des widgets tkinter (voir ci-après). Ainsi l’objet référencé dans self.chk contient l’équivalent d’une variable de type entier, dans un format utilisable par tkinter. Pour accéder à sa valeur depuis Python, il faut utiliser des méthodes spécifiques de cette classe d’objets : la méthode set() permet de lui assigner une valeur, et la méthode get() permet de la récupérer (ce que l’on mettra en pratique à la ligne 47).

• Ligne 12 : L’option variable de l’objet checkbutton est associée à la variable tkinter définie à la ligne précédente. Nous ne pouvons pas référencer directement une variable ordinaire dans la définition d’un widget tkinter, parce que tkinter lui-même est écrit dans un langage qui n’utilise pas les mêmes conventions que Python pour formater ses variables. Les objets construits à partir des classes de variables tkinter sont donc nécessaires pour assurer l’interface.

• Ligne 13 : L’option command désigne la méthode que le système doit invoquer lorsque l’utilisa- teur effectue un clic de souris dans la case à cocher.

• Lignes 14 à 24 : Ces lignes définissent les trois widgets curseurs, en trois instructions similaires. Il serait plus élégant de programmer tout ceci en une seule instruction, répétée trois fois à l’aide d’une boucle. Cela nécessiterait cependant de faire appel à un concept que nous n’avons pas encore expliqué (les fonctions ou expressions lamdba), et la définition du gestionnaire d’évènements associé à ces widgets deviendrait elle aussi plus complexe. Conservons donc pour cette fois des instructions séparées : nous nous efforcerons d’améliorer tout cela plus tard.

• Lignes 26 à 40 : Les 4 widgets définis dans les lignes précédentes possèdent chacun une option command. Pour chacun d’eux, la méthode invoquée dans cette option command est différente : la case à cocher active la méthode setCurve(), le premier curseur active la méthode setFrequen- cy(), le second curseur active la méthode setPhase(), et le troisième curseur active la méthode setAmplitude().

Remarquez bien au passage que l’option command des widgets Scale transmet un argument à la méthode associée (la position actuelle du curseur), alors que la même option command ne transmet rien dans le cas du widget Checkbutton.

Ces 4 méthodes (qui sont donc les gestionnaires des évènements produits par la case à cocher et les trois curseurs) provoquent elles-mêmes chacune l’émission d’un nouvel évènement, en faisant appel à la méthode event_generate().

Lorsque cette méthode est invoquée, Python envoie au système d’exploitation exactement le même message évènement que celui qui se produirait si l’utilisateur enfonçait simultanément les touches <Ctrl>, <Maj> et <Z> de son clavier. Nous produisons ainsi un message-évènement bien particulier, qui peut être détecté et traité par un gestionnaire d’évènement associé à un autre widget (voir page suivante).

De cette manière, nous mettons en place un véritable système de communication entre widgets : chaque fois que l’utilisateur exerce une action sur notre panneau de contrôle, celui-ci génère un évènement spécifique, qui signale cette action à l’attention des autres widgets présents. Nous aurions pu choisir une autre combinaison de touches (ou même carrément un autre type d’évènement). Notre choix s’est porté sur celle-ci parce qu’il y a vraiment très peu de chances que l’utilisateur s’en serve alors qu’il examine notre programme.

Nous pourrons cependant produire nous-mêmes un tel évènement au clavier à titre de test, lorsque le moment sera venu de vérifier le gestionnaire de cet évènement, que nous mettrons en place par ailleurs.

• Lignes 42 à 54 : Comme nous l’avions déjà fait pour oscillo.py, nous complétons ce nouveau module par quelques lignes de code au niveau principal. Ces lignes permettent de tester le bon fonctionnement de la classe : elles ne s’exécutent que si on lance le module directement, comme une application à part entière.

Veillez à utiliser vous-même cette technique dans vos propres modules, car elle constitue une bonne pratique de programmation : l’utilisateur de modules construits ainsi peut en effet (re)découvrir très aisément leur fonctionnalité (en les exécutant) et la manière de s’en servir (en analysant ces quelques lignes de code). a Dans ces lignes de test, nous construisons une fenêtre principale root qui contient deux widgets : un widget de la nouvelle classe ChoixVibra() et un widget de la classe Label().

À la ligne 53, nous associons à la fenêtre principale un gestionnaire d’évènement : tout évènement du type spécifié déclenche désormais un appel de la fonction afficherTout(). Cette fonction est donc notre gestionnaire d’événement spécialisé, qui est sollicité chaque fois qu’un évènement de type <Maj-Ctrl-Z> est détecté par le système d’exploitation.

Comme nous l’avons déjà expliqué plus haut, nous avons fait en sorte que de tels événements soient produits par les objets de la classe ChoixVibra(), chaque fois que l’utilisateur modifie l’état de l’un ou l’autre des trois curseurs, ou celui de la case à cocher.

• Conçue seulement pour effectuer un test, la fonction afficherTout() ne fait rien d’autre que provoquer l’affichage des valeurs des variables associées à chacun de nos quatre widgets, en (re)configurant l’option text d’un widget de classe Label().

 Ligne 47, expression fra.chk.get() : nous avons vu plus haut que la variable mémorisant l’état de la case à cocher est un objet-variable tkinter. Python ne peut pas lire directement le contenu d’une telle variable, qui est en réalité un objet-interface. Pour en extraire la valeur, il faut donc faire usage d’une méthode spécifique de cette classe d’objets : la méthode get().

Propagation des évènements Le mécanisme de communication décrit ci-dessus respecte la hiérarchie de classes des widgets. Vous aurez noté que la méthode qui déclenche l’évènement est associée au widget dont nous sommes en train de définir la classe, par l’intermédiaire de self.

En général, un message-évènement est en effet associé à un widget particulier (par exemple, un clic de souris sur un bouton est associé à ce bouton), ce qui signifie que le système d’exploitation va d’abord examiner s’il existe un gestionnaire pour ce type d’évènement, qui soit lui aussi associé à ce widget.

S’il en existe un, c’est celui-là qui est activé, et la propagation du message s’arrête. Sinon, le message-évènement est « présenté » successivement aux widgets maîtres, dans l’ordre hiérarchique, jusqu’à ce qu’un gestionnaire d’évènement soit trouvé, ou bien jusqu’à ce que la fenêtre principale soit atteinte.

Les évènements correspondant à des frappes sur le clavier (telle la combinaison de touches <Maj-Ctrl- Z> utilisée dans notre exercice) sont cependant toujours expédiés directement à la fenêtre principale de l’application. Dans notre exemple, le gestionnaire de cet évènement doit donc être associé à la fenêtre root.

Exercices

13.13 Votre nouveau widget hérite des propriétés de la classe Frame(). Vous pouvez donc modifier son aspect en modifiant les options par défaut de cette classe, à l’aide de la méthode confi- gure(). Essayez par exemple de faire en sorte que le panneau de contrôle soit entouré d’une bordure de 4 pixels ayant l’aspect d’un sillon (bd = 4, relief = GROOVE). Si vous ne comprenez pas bien ce qu’il faut faire, inspirez-vous du script oscillo.py (ligne 10).

13.14 Si l’on assigne la valeur 1 à l’option showvalue des widgets Scale(), la position précise du curseur par rapport à l’échelle est affichée en permanence. Activez donc cette fonctionnalité pour le curseur qui contrôle le paramètre « phase ».

13.15 L’option troughcolor des widgets Scale() permet de définir la couleur de leur glissière. Utilisez cette option pour faire en sorte que la couleur des glissières des 3 curseurs soit celle qui est utilisée comme paramètre lors de l’instanciation de votre nouveau widget.

13.16 Modifiez le script de telle manière que les widgets curseurs soient écartés davantage les uns des autres (options padx et pady de la méthode pack()).

Intégration de widgets composites dans une application synthèse

Dans les exercices précédents, nous avons construit deux nouvelles classes de widgets : le widget Oscillo- Graphe(), canevas spécialisé pour le dessin de sinusoïdes, et le widget ChoixVibra(), panneau de contrôle à trois curseurs permettant de choisir les paramètres d’une vibration.

Ces widgets sont désormais disponibles dans les modules oscillo.py et curseurs.py. Nous allons à présent les utiliser dans une application synthèse : un widget OscilloGraphe() y affiche un, deux, ou trois graphiques superposés, de couleurs différentes, chacun d’entre eux étant soumis au contrôle d’un widget ChoixVibra().

Le script correspondant est reproduit ci-après. Nous attirons votre attention sur la technique mise en œuvre pour provoquer un rafraîchissement de l’affichage dans le canevas par l’intermédiaire d’un évènement, chaque fois que l’utilisateur effectue une action quelconque au niveau de l’un des panneaux de contrôle. Rappelez-vous que les applications destinées à fonctionner dans une interface graphique doivent être conçues comme des « programmes pilotés par les évènements ».

En préparant cet exemple, nous avons arbitrairement décidé que l’affichage des graphiques serait déclenché par un évènement particulier, tout à fait similaire à ceux que génère le système d’exploitation lorsque l’utilisateur accomplit une action quelconque. Dans la gamme (très étendue) d’évènements possibles, nous en avons choisi un qui ne risque guère d’être utilisé pour d’autres raisons, pendant que notre application fonctionne : la combinaison de touches <Maj-Ctrl-Z>.

Lorsque nous avons construit la classe de widgets ChoixVibra(), nous y avons donc incorporé les instructions nécessaires pour que de tels évènements soient générés chaque fois que l’utilisateur actionne l’un des curseurs ou modifie l’état de la case à cocher.

Nous allons à présent définir le gestionnaire de cet évènement et l’inclure dans notre nouvelle classe : nous l’appellerons montre- Courbes() et il se chargera de rafraîchir l’affichage. Étant donné que l’évènement concerné est du type <enfoncement d’une touche>, nous devrons cependant le détecter au niveau de la fenêtre principale de l’application.

1# from oscillo import *
2# from curseurs import *
3#
4# class ShowVibra(Frame):
5#     """Démonstration de mouvements vibratoires harmoniques"""
6#     def __init__(self, boss =None):
7#          Frame.__init__(self) # constructeur de la classe parente
8#          self.couleur = ['dark green', 'red', 'purple']
9#          self.trace = [0]*3 # liste des tracés (courbes à dessiner)
10#         self.controle = [0]*3 # liste des panneaux de contrôle
11#
12#         # Instanciation du canevas avec axes X et Y :
13#         self.gra = OscilloGraphe(self, larg =400, haut=200)
14#         self.gra.configure(bg ='white', bd=2, relief=SOLID)
15#         self.gra.pack(side =TOP, pady=5)
16#
17#         # Instanciation de 3 panneaux de contrôle (curseurs) :
18#         for i in range(3):
19#             self.controle[i] = ChoixVibra(self, self.couleur[i])
20#             self.controle[i].pack()
21#
22#         # Désignation de l'événement qui déclenche l'affichage des tracés :
23#         self.master.bind('<Control-Z>', self.montreCourbes)
24#         self.master.title('Mouvements vibratoires harmoniques')
25#         self.pack()
26#
27# def montreCourbes(self, event):
28#     """(Ré)Affichage des trois graphiques élongation/temps"""
29#     for i in range(3):
30#
31#         # D'abord, effacer le tracé précédent (éventuel) :
32#         self.gra.delete(self.trace[i])
33#
34#         # Ensuite, dessiner le nouveau tracé :
35#         if self.controle[i].chk.get():
36#             self.trace[i] = self.gra.traceCourbe(
37#                 coul = self.couleur[i],
38#                 freq = self.controle[i].freq,
39#                 phase = self.controle[i].phase,
40#                 ampl = self.controle[i].ampl)
41#
42# #### Code pour tester la classe : ###
43#
44# if __name__ == '__main__':
45#     ShowVibra().mainloop()

Commentaires

• Lignes 1-2 : Nous pouvons nous passer d’importer le module tkinter : chacun de ces deux modules s’en charge déjà.

• Ligne 4 : Puisque nous commençons à connaître les bonnes techniques, nous décidons de construire l’application elle-même sous la forme d’une nouvelle classe de widget, dérivée de la classe Frame() : ainsi nous pourrons plus tard l’intégrer toute entière dans d’autres projets, si le cœur nous en dit.

• Lignes 8-10 : Définition de quelques variables d’instance (3 listes) : les trois courbes tracées seront des objets graphiques, dont les couleurs sont prédéfinies dans la liste self.couleur ; nous devons préparer également une liste self.trace pour mémoriser les références de ces objets graphiques, et enfin une liste self.controle pour mémoriser les références des trois panneaux de contrôle.

• Lignes 13 à 15 : Instanciation du widget d’affichage. Étant donné que la classe OscilloGraphe() a été obtenue par dérivation de la classe Canvas(), il est toujours possible de configurer ce widget en redéfinissant les options spécifiques de cette classe (ligne 13).

• Lignes 18 à 20 : Pour instancier les trois widgets « panneau de contrôle », on utilise une boucle. Leurs références sont mémorisées dans la liste self.controle préparée à la ligne 10. Ces panneaux de contrôle sont instanciés comme esclaves du présent widget, par l’intermédiaire du paramètre self. Un second paramètre leur transmet la couleur du tracé à contrôler.

• Lignes 23-24 : Au moment de son instanciation, chaque widget tkinter reçoit automatiquement un attribut master qui contient la référence de la fenêtre principale de l’application. Cet attribut se révèle particulièrement utile si la fenêtre principale a été instanciée implicitement par tkinter, comme c’est le cas ici.

Rappelons en effet que lorsque nous démarrons une application en instanciant directement un widget tel que Frame(), par exemple (c’est ce que nous avons fait à la ligne 4), tkinter instancie automatiquement une fenêtre maîtresse pour ce widget (un objet de la classe Tk()).

Comme cet objet a été créé automatiquement, nous ne disposons d’aucune référence dans notre code pour y accéder, si ce n’est par l’intermédiaire de cet attribut master que tkinter associe automatiquement à chaque widget. Nous nous servons de cette référence pour redéfinir le bandeau-titre de la fenêtre principale (à la ligne 24), et pour y attacher un gestionnaire d’événement (à la ligne 23).

• Lignes 27 à 40 : La méthode décrite ici est le gestionnaire des événements <Maj-Ctrl-Z> spécifiquement déclenchés par nos widgets ChoixVibra() (ou « panneaux de contrôle »), chaque fois que l’utilisateur exerce une action sur un curseur ou une case à cocher.

Dans tous les cas, les graphiques éventuellement présents sont d’abord effacés (ligne 28) à l’aide de la méthode delete() : le widget OscilloGraphe() a hérité cette méthode de sa classe parente Canvas(). Ensuite, de nouvelles courbes sont retracées, pour chacun des panneaux de contrôle dont on a coché la case « Afficher ».

Chacun des objets ainsi dessinés dans le canevas possède un numéro de référence, renvoyé par la méthode traceCourbe() de notre widget OscilloGraphe(). Les numéros de référence de nos dessins sont mémorisés dans la liste self.trace. Ils permettent d’effacer individuellement chacun d’entre eux (cf. instruction de la ligne 28).

• Lignes 38-40 : Les valeurs de fréquence, phase et amplitude que l’on transmet à la méthode trace- Courbe() sont les attributs d’instance correspondants de chacun des trois panneaux de contrôle, eux-mêmes mémorisés dans la liste self.controle. Nous pouvons récupérer ces attributs en utilisant la qualification des noms par points.

Exercices

13.17 Modifiez le script, de manière à obtenir l’aspect ci-dessous (écran d’affichage avec grille de référence, panneaux de contrôle entourés d’un sillon) :

13.18 Modifiez le script, de manière à faire apparaître et contrôler 4 graphiques au lieu de trois. Pour la couleur du quatrième graphique, choisissez par exemple : blue, navy, maroon...

13.19 Aux lignes 33-35, nous récupérons les valeurs des fréquence, phase et amplitude choisies par l’utilisateur sur chacun des trois panneaux de contrôle, en accédant directement aux attributs d’instance correspondants. Python autorise ce raccourci – et c’est bien pratique – mais cette technique est dangereuse.

Elle enfreint l’une des recommandations de la théorie générale de la « programmation orientée objet », qui préconise que l’accès aux propriétés des objets soit toujours pris en charge par des méthodes spécifiques. Pour respecter cette recommandation, ajoutez à la classe ChoixVibra() une méthode supplémentaire que vous appellerez valeurs(), et qui renverra un tuple contenant les valeurs de la fréquence, la phase et l’amplitude choisies. Les lignes 33 à 35 du présent script pourront alors être remplacées par quelque chose comme : freq, phase, ampl = self.control[i].valeurs()

13.20 Écrivez une petite application qui fait apparaître une fenêtre avec un canevas et un widget curseur (Scale). Dans le canevas, dessinez un cercle, dont l’utilisateur pourra faire varier la taille à l’aide du curseur.

13.21 Écrivez un script qui créera deux classes : une classe Application, dérivée de Frame(), dont le constructeur instanciera un canevas de 400 × 400 pixels, ainsi que deux boutons. Dans le canevas, vous instancierez un objet de la classe Visage décrite ci-après.

La classe Visage servira à définir des objets graphiques censés représenter des visages humains simplifiés. Ces visages seront constitués d’un cercle principal dans lequel trois ovales plus petits représenteront deux yeux et une bouche (ouverte).

Une méthode « fermer » permettra de remplacer l’ovale de la bouche par une ligne horizontale. Une méthode « ou- vrir » permettra de restituer la bouche de forme ovale. Les deux boutons définis dans la classe Application serviront respectivement à fermer et à ouvrir la bouche de l’objet Visage installé dans le canevas. Vous pouvez vous inspirer de l’exemple de la page 88 pour composer une partie du code.

13.22 Exercice de synthèse : élaboration d’un dictionnaire de couleurs.

But : réaliser un petit programme utilitaire, qui puisse vous aider à construire facilement et rapidement un nouveau dictionnaire de couleurs, lequel permettrait l’accès technique à une couleur quelconque par l’intermédiaire de son nom usuel en français.

Contexte : en manipulant divers objets colorés avec tkinter, vous avez constaté que cette bibliothèque graphique accepte qu’on lui désigne les couleurs les plus fondamentales sous la forme de chaînes de caractères contenant leur nom en anglais : red, blue, yellow, etc. Vous savez cependant qu’un ordinateur ne peut traiter que des informations numérisées. Cela implique que la désignation d’une couleur quelconque doit nécessairement tôt ou tard être encodée sous la forme d’un nombre. Il faut bien entendu adopter pour cela une une convention, et celle-ci peut varier d’un système à un autre.

L’une de ces conventions, parmi les plus courantes, consiste à représenter une couleur à l’aide de trois octets, qui indiqueront respectivement les intensités des trois composantes rouge, verte et bleue de cette couleur. Cette convention peut être utilisée avec tkinter pour accéder à n’importe quelle nuance colorée. Vous pouvez en effet lui indiquer la couleur d’un élément graphique quelconque, à l’aide d’une chaîne de 7 caractères telle que ’#00FA4E’.

Dans cette chaîne, le premier caractère (#) signifie que ce qui suit est une valeur hexadécimale. Les six caractères suivants représentent les 3 valeurs hexadécimales des 3 composantes rouge, vert et bleu. Pour visualiser concrètement la correspondance entre une couleur quelconque et son code, vous pouvez explorer les ressources de divers programmes de traitement d’images, tels les excellents programmes libres Gimp et Inkscape, par exemple.

Étant donné qu’il n’est pas facile pour les humains que nous sommes de mémoriser de tels codes hexadécimaux, tkinter est également doté d’un dictionnaire de conversion, qui autorise l’utilisation de noms communs pour un certain nombre de couleurs parmi les plus courantes, mais cela ne marche que pour des noms de couleurs exprimés en anglais.

Le but du présent exercice est de réaliser un logiciel qui facilitera la construction d’un dictionnaire équivalent en français, lequel pourrait ensuite être incorporé à l’un ou l’autre de vos propres programmes. Une fois construit, ce dictionnaire serait donc de la forme :

{'vert':'#00FF00', 'bleu':'#0000FF', ... etc ...}.

Cahier des charges :

L’application à réaliser sera une application graphique, construite autour d’une classe. Elle comportera une fenêtre avec un certain nombre de champs d’entrée et de boutons, afin que l’utilisateur puisse aisément encoder de nouvelles couleurs en indiquant à chaque fois son nom français dans un champ, et son code hexadécimal dans un autre.

Lorsque le dictionnaire contiendra déjà un certain nombre de données, il devra être possible de le tester, c’est-à-dire d’entrer un nom de couleur en français et de retrouver le code hexadécimal correspondant à l’aide d’un bouton (avec affichage éventuel d’une zone colorée). Un bouton provoquera l’enregistrement du dictionnaire dans un fichier texte. Un autre permettra de reconstruire le dictionnaire à partir du fichier.

13.23 Le script ci-dessous correspond à une ébauche de projet dessinant des ensembles de dés à jouer disposés à l’écran de plusieurs manières différentes (cette ébauche pourrait être une première étape dans la réalisation d’un logiciel de jeu). L’exercice consistera à analyser ce script et à le compléter. Vous vous placerez ainsi dans la situation d’un programmeur chargé de continuer le travail commencé par quelqu’un d’autre, ou encore dans celle de l’informaticien prié de participer à un travail d’équipe.

A) Commencez par analyser ce script et ajoutez-y des commentaires, en particulier aux lignes marquées : #***, pour montrer que vous comprenez ce que doit faire le programme à ces emplacements :

from tkinter import *

class FaceDom(object):
    def __init__(self, can, val, pos, taille =70):
        self.can =can
        # ***
        x, y, c = pos[0], pos[1], taille/2
        can.create_rectangle(x -c, y-c, x+c, y+c, fill ='ivory', width =2)
        d = taille/3
        # ***
        self.pList =[]
        # ***
        pDispo = [((0,0),), ((-d,d),(d,-d)), ((-d,-d), (0,0), (d,d))]
        disp = pDispo[val -1]
        # ***
        for p in disp:
            self.cercle(x +p[0], y +p[1], 5, 'red')

def cercle(self, x, y, r, coul):
    # ***
    self.pList.append(self.can.create_oval(x-r, y-r, x+r, y+r, fill=coul))

def effacer(self):
    # ***
    for p in self.pList:
        self.can.delete(p)

class Projet(Frame):
    def __init__(self, larg, haut):
        Frame.__init__(self)
        self.larg, self.haut = larg, haut
        self.can = Canvas(self, bg='dark green', width =larg, height =haut)
        self.can.pack(padx =5, pady =5)
        # ***
        bList = [("A", self.boutA), ("B", self.boutB),
        ("C", self.boutC), ("D", self.boutD),
        ("Quitter", self.boutQuit)]
        for b in bList:
            Button(self, text =b[0], command =b[1]).pack(side =LEFT)
    self.pack()

def boutA(self):
    self.d3 = FaceDom(self.can, 3, (100,100), 50)

def boutB(self):
    self.d2 = FaceDom(self.can, 2, (200,100), 80)

def boutC(self):
    self.d1 = FaceDom(self.can, 1, (350,100), 110)

def boutD(self):
        # ***
        self.d3.effacer()
def boutQuit(self):
    self.master.destroy()

Projet(500, 300).mainloop()

B) Modifiez ensuite ce script, afin qu’il corresponde au cahier des charges suivant : Le canevas devra être plus grand : 600 × 600 pixels. Les boutons de commande devront être déplacés à droite et espacés davantage. La taille des points sur une face de dé devra varier proportionnellement à la taille de cette face.

Variante 1 : Ne conservez que les 2 boutons <A> et <B>.

Chaque utilisation du bouton <A> fera apparaître 3 nouveaux dés (de même taille, plutôt petits) disposés sur une colonne (verticale), les valeurs de ces dés étant tirées au hasard entre 1 et 6. Chaque nouvelle colonne sera disposée à la droite de la précédente. Si l’un des tirages de 3 dés correspond à 4, 2, 1 (dans n’importe quel ordre), un message « gagné » sera affiché dans la fenêtre (ou dans le canevas). Le bouton <B> provoquera l’effacement complet (pas seulement les points !) de tous les dés affichés.

Variante 2 : Ne conservez que les 2 boutons <A> et <B>.

Le bouton <A> fera apparaître 5 dés disposés en quinconce (c’est-à-dire comme les points d’une face de valeur 5). Les valeurs de ces dés seront tirées au hasard entre 1 et 6, mais il ne pourra pas y avoir de doublons. Le bouton <B> provoquera l’effacement complet (pas seulement les points !) de tous les dés affichés.

Variante 3 : Ne conservez que les 3 boutons <A>, <B> et <C>.

Le bouton <A> fera apparaître 13 dés de même taille disposés en cercle.

Chaque utilisation du bouton <B> provoquera un changement de valeur du premier dé, puis du deuxième, du troisième, etc. La nouvelle valeur d’un dé sera à chaque fois égale a sa valeur précédente augmentée d’une unité, sauf dans le cas ou la valeur précédente était 6 : dans ce cas la nouvelle valeur est 1, et ainsi de suite. Le bouton <C> provoquera l’effacement complet (pas seulement les points !) de tous les dés affichés.

Variante 4 : Ne conservez que les 3 boutons <A>, <B> et <C>.

Le bouton <A> fera apparaître 12 dés de même taille disposés sur deux lignes de 6. Les valeurs des dés de la première ligne seront dans l’ordre 1, 2, 3, 4, 5, 6. Les valeurs des dés de la seconde ligne seront tirées au hasard entre 1 et 6.

Chaque utilisation du bouton <B> provoquera un changement de valeur aléatoire du premier dé de la seconde ligne, tant que cette valeur restera différente de celle du dé correspondant dans la première ligne. Lorsque le 1er dé de la 2e ligne aura acquis la valeur de son correspondant, c’est la valeur du 2e dé de la seconde ligne qui sera changée au hasard, et ainsi de suite, jusqu’à ce que les 6 faces du bas soient identiques à celles du haut. Le bouton <C> provoquera l’effacement complet (pas seulement les points !) de tous les dés affichés.

Solutions des exercices

Exercice 13.6 :

from tkinter import *
def cercle(can, x, y, r, coul ='white'):
    "dessin d'un cercle de rayon <r> en <x,y> dans le canevas <can>"
    can.create_oval(x-r, y-r, x+r, y+r, fill =coul)

class Application(Tk):
    def __init__(self):
        Tk.__init__(self) # constructeur de la classe parente
        self.can =Canvas(self, width =475, height =130, bg ="white")
        self.can.pack(side =TOP, padx =5, pady =5)
        Button(self, text ="Train", command =self.dessine).pack(side =LEFT)
        Button(self, text ="Hello", command =self.coucou).pack(side =LEFT)
        Button(self, text ="Ecl34", command =self.eclai34).pack(side =LEFT)

    def dessine(self):
        "instanciation de 4 wagons dans le canevas"
        self.w1 = Wagon(self.can, 10, 30)
        self.w2 = Wagon(self.can, 130, 30, 'dark green')
        self.w3 = Wagon(self.can, 250, 30, 'maroon')
        self.w4 = Wagon(self.can, 370, 30, 'purple')

    def coucou(self):
        "apparition de personnages dans certaines fenêtres"
        self.w1.perso(3) # 1er wagon, 3e fenêtre
        self.w3.perso(1) # 3e wagon, 1e fenêtre
        self.w3.perso(2) # 3e wagon, 2e fenêtre
        self.w4.perso(1) # 4e wagon, 1e fenêtre

    def eclai34(self):
        "allumage de l'éclairage dans les wagons 3 & 4"
        self.w3.allumer()
        self.w4.allumer()

class Wagon(object):
    def __init__(self, canev, x, y, coul ='navy'):
        "dessin d'un petit wagon en <x,y> dans le canevas <canev>"
        # mémorisation des paramètres dans des variables d'instance :
        self.canev, self.x, self.y = canev, x, y
        # rectangle de base : 95x60 pixels :
        canev.create_rectangle(x, y, x+95, y+60, fill =coul)
        # 3 fenêtres de 25x40 pixels, écartées de 5 pixels :
        self.fen =[] # pour mémoriser les réf. des fenêtres
        for xf in range(x +5, x +90, 30):
            self.fen.append(canev.create_rectangle(xf, y+5,
                xf+25, y+40, fill ='black'))
        # 2 roues, de rayon égal à 12 pixels :
        cercle(canev, x+18, y+73, 12, 'gray')
        cercle(canev, x+77, y+73, 12, 'gray')

    def perso(self, fen):
        "apparition d'un petit personnage à la fenêtre <fen>"
        # calcul des coordonnées du centre de chaque fenêtre :
        xf = self.x + fen*30 -12
        yf = self.y + 25
        cercle(self.canev, xf, yf, 10, "pink") # visage
        cercle(self.canev, xf-5, yf-3, 2) # œil gauche
        cercle(self.canev, xf+5, yf-3, 2) # œil droit
        cercle(self.canev, xf, yf+5, 3) # bouche

    def allumer(self):
        "déclencher l'éclairage interne du wagon"
        for f in self.fen:
            self.canev.itemconfigure(f, fill ='yellow')

app = Application()
app.mainloop()

Exercice 13.10 :

# Widget dérivé de <Canvas>, spécialisé pour
# dessiner des graphiques élongation/temps

from tkinter import *
from math import sin, pi

class OscilloGraphe(Canvas):
    "Canevas spécialisé, pour dessiner des courbes élongation/temps"
    def __init__(self, master=None, larg=200, haut=150):
        "Constructeur de la base du graphique : quadrillage et axes"
        Canvas.__init__(self) # appel au constructeur
        self.configure(width=larg, height=haut) # de la classe parente
        self.larg, self.haut = larg, haut # mémorisation
        # tracé d'une échelle horizontale avec 8 graduations :
        pas = (larg-25)/8. # intervalles de l'échelle horizontale
        for t in range(0, 9):
            stx = 10 + t*pas # +10 pour partir de l'origine
            self.create_line(stx, haut/10, stx, haut*9/10, fill='grey')
        # tracé d'une échelle verticale avec 5 graduations :
        pas = haut*2/25. # intervalles de l'échelle verticale
        for t in range(-5, 6):
            sty = haut/2 -t*pas # haut/2 pour partir de l'origine
            self.create_line(10, sty, larg-15, sty, fill='grey')
        self.traceAxes() # tracé des axes de référence X et Y

def traceAxes(self):
    "Méthode traçant les axes de référence (pourra être surchargée)."
    # axes horizontal (X) et vertical (Y) :
    self.create_line(10, self.haut/2, self.larg, self.haut/2, arrow=LAST)
    self.create_line(10, self.haut-5, 10, 5, arrow=LAST)
    # indication des grandeurs physiques aux extrémités des axes :
    self.create_text(20, 10, anchor =CENTER, text = "e")
    self.create_text(self.larg-10, self.haut/2-12, anchor=CENTER, text="t")

def traceCourbe(self, freq=1, phase=0, ampl=10, coul='red'):
    "tracé d'un graphique élongation/temps sur 1 seconde"
    curve =[] # liste des coordonnées
    pas = (self.larg-25)/1000. # l'échelle X correspond à 1 seconde
    for t in range(0,1001,5): # que l'on divise en 1000 ms.
        e = ampl*sin(2*pi*freq*t/1000 - phase)
    x = 10 + t*pas
    y = self.haut/2 - e*self.haut/25
    curve.append((x,y))
n = self.create_line(curve, fill=coul, smooth=1)
return n # n = numéro d'ordre du tracé

# Tracé de graphiques élongation/temps pour 3
# mouvements vibratoires harmoniques

from tkinter import *
from math import sin, pi
from exercice_13_10 import OscilloGraphe

class OscilloGrapheBis(OscilloGraphe):
    """Classe dérivée du widget Oscillographe (cf. exercice 13.10)"""
    def __init__(self, master =None, larg =200, haut =150):
        # Appel du constructeur de la classe parente :
        OscilloGraphe.__init__(self, master, larg, haut)

    def traceAxes(self):
        "Surchage de la méthode de même nom dans la classe parente"
        # tracé de l'axe de référence Y :
        pas = (self.larg-25)/8. # intervalles de l'échelle horizontale
        self.create_line(10+4*pas, self.haut-5, 10+4*pas, 5, fill ='grey90',
        arrow=LAST)
        # tracé de l'axe de référence X :
        self.create_line(10, self.haut/2, self.larg, self.haut/2,
        fill= 'grey90', arrow=LAST)
        # indication des grandeurs physiques aux extrémités des axes :
        self.create_text(20+4*pas, 15, anchor=CENTER, text="e", fill='red')
        self.create_text(self.larg-5, self.haut/2-12, anchor=CENTER, text ="t",
            fill='red')

class ChoixVibra(Frame):
    """Curseurs pour choisir fréquence, phase & amplitude d'une vibration"""
    def __init__(self, master=None, coul='red'):
        Frame.__init__(self) # constructeur de la classe parente
        # Définition de quelques attributs d'instance :
        self.freq, self.phase, self.ampl, self.coul = 0, 0, 0, coul
        # Variable d'état de la case à cocher :
        self.chk = IntVar() # 'objet-variable' Tkinter
        Checkbutton(self, text='Afficher', variable=self.chk,
            fg = self.coul, command=self.setCurve).pack(side=LEFT)
    # Définition des 3 widgets curseurs :
    Scale(self, length=150, orient=HORIZONTAL, sliderlength =25,
        label ='Fréquence (Hz) :', from_=1., to=9., tickinterval =2,
        resolution =0.25, showvalue =0,
        command = self.setFrequency).pack(side=LEFT, pady =5)
    Scale(self, length=150, orient=HORIZONTAL, sliderlength =15,
        label ='Phase (degrés) :', from_=-180, to=180, tickinterval =90,
        showvalue =0, command = self.setPhase).pack(side=LEFT, pady =5)
    Scale(self, length=150, orient=HORIZONTAL, sliderlength =25,
        label ='Amplitude :', from_=2, to=10, tickinterval =2,
        showvalue =0,
        command = self.setAmplitude).pack(side=LEFT, pady =5)
    def setCurve(self):
        self.master.event_generate('<Control-Z>')
    def setFrequency(self, f):
        self.freq = float(f)
        self.master.event_generate('<Control-Z>')
    def setPhase(self, p):
        pp =float(p)
        self.phase = pp*2*pi/360 # conversion degrés -> radians
        self.master.event_generate('<Control-Z>')
    def setAmplitude(self, a):
        self.ampl = float(a)
        self.master.event_generate('<Control-Z>')

## Classe principale ##

class ShowVibra(Frame):
    """Démonstration de mouvements vibratoires harmoniques"""
    def __init__(self, master=None):
        Frame.__init__(self) # constructeur de la classe parente
        self.couleur = ['green', 'yellow', 'orange']
        self.trace = [0]*3 # liste des tracés (courbes à dessiner)
        self.controle = [0]*3 # liste des panneaux de contrôle
        # Instanciation du canevas avec axes X et Y :
        self.gra = OscilloGrapheBis(self, larg =400, haut=300)
        self.gra.configure(bg ='grey40', bd=3, relief=SUNKEN)
        self.gra.pack(side =TOP, pady=3)
        # Instanciation de 3 panneaux de contrôle (curseurs) :
        for i in range(3):
            self.controle[i] = ChoixVibra(self, self.couleur[i])
            self.controle[i].configure(bd =3, relief = GROOVE)
            self.controle[i].pack(padx =10, pady =3)
        # Désignation de l'événement qui déclenche l'affichage des tracés :
        self.master.bind('<Control-Z>', self.montreCourbes)
        self.master.title('Mouvements vibratoires harmoniques')
        self.pack()

        def montreCourbes(self, event):
            """(Ré)Affichage des trois graphiques élongation/temps"""
            for i in range(3):
                # D'abord, effacer le tracé précédent (éventuel) :
                self.gra.delete(self.trace[i])
                # Ensuite, dessiner le nouveau tracé :
                if self.controle[i].chk.get():
                    self.trace[i] = self.gra.traceCourbe(
                    coul=self.couleur[i],
                    freq=self.controle[i].freq,
                    phase=self.controle[i].phase,
                    ampl=self.controle[i].ampl)
#### Code de test : ###
if __name__ == '__main__':
    ShowVibra().mainloop()

Exercice 13.22 : Dictionnaire de couleurs

from tkinter import *
# Module donnant accès aux boîtes de dialogue standard pour
# la recherche de fichiers sur disque :
from tkinter.filedialog import asksaveasfile, askopenfile

class Application(Frame):
    '''Fenêtre d'application'''
    def __init__(self):
        Frame.__init__(self)
        self.master.title("Création d'un dictionnaire de couleurs")
        self.dico ={} # création du dictionnaire
        # Les widgets sont regroupés dans deux cadres (Frames) :
        frSup =Frame(self) # cadre supérieur contenant 6 widgets
        Label(frSup, text ="Nom de la couleur :",
        width =20).grid(row =1, column =1)
        self.enNom =Entry(frSup, width =25) # champ d'entrée pour
        self.enNom.grid(row =1, column =2) # le nom de la couleur
        Button(frSup, text ="Existe déjà ?", width =12,
        command =self.chercheCoul).grid(row =1, column =3)
        Label(frSup, text ="Code hexa. corresp. :",
            width =20).grid(row =2, column =1)
        self.enCode =Entry(frSup, width =25) # champ d'entrée pour
        self.enCode.grid(row =2, column =2) # le code hexa.
        Button(frSup, text ="Test", width =12,
        command =self.testeCoul).grid(row =2, column =3)
        frSup.pack(padx =5, pady =5)

        frInf =Frame(self) # cadre inférieur contenant le reste
        self.test = Label(frInf, bg ="white", width =45, # zone de test
            height =7, relief = SUNKEN)
        self.test.pack(pady =5)
        Button(frInf, text ="Ajouter la couleur au dictionnaire",
            command =self.ajouteCoul).pack()
        Button(frInf, text ="Enregistrer le dictionnaire", width =25,
            command =self.enregistre).pack(side = LEFT, pady =5)
        Button(frInf, text ="Restaurer le dictionnaire", width =25,
            command =self.restaure).pack(side =RIGHT, pady =5)
        frInf.pack(padx =5, pady =5)
        self.pack()

    def ajouteCoul(self):
        "ajouter la couleur présente au dictionnaire"
        if self.testeCoul() ==0: # une couleur a-t-elle été définie ?
            return
        nom = self.enNom.get()
        if len(nom) >1: # refuser les noms trop petits
            self.dico[nom] =self.cHexa
        else:
            self.test.config(text ="%s : nom incorrect" % nom, bg='white')

    def chercheCoul(self):
        "rechercher une couleur déjà inscrite au dictionnaire"
        nom = self.enNom.get()
        if nom in self.dico:
            self.test.config(bg =self.dico[nom], text ="")
        else:
            self.test.config(text ="%s : couleur inconnue" % nom, bg='white')

    def testeCoul(self):
        "vérifier la validité d'un code hexa. - afficher la couleur corresp."
        try:
            self.cHexa =self.enCode.get()
            self.test.config(bg =self.cHexa, text ="")
            return 1
        except:
            self.test.config(text ="Codage de couleur incorrect", bg ='white')
            return 0
    def enregistre(self):
        "enregistrer le dictionnaire dans un fichier texte"
        # Cette méthode utilise une boîte de dialogue standard pour la
        # sélection d'un fichier sur disque. Tkinter fournit toute une série
        # de fonctions associées à ces boîtes, dans le module filedialog.
        # La fonction ci-dessous renvoie un objet-fichier ouvert en écriture :
        ofi =asksaveasfile(filetypes=[("Texte",".txt"),("Tous","*")])
        for clef, valeur in list(self.dico.items()):
            ofi.write("{0} {1}\n".format(clef, valeur))
            ofi.close()
    def restaure(self):
        "restaurer le dictionnaire à partir d'un fichier de mémorisation"
        # La fonction ci-dessous renvoie un objet-fichier ouvert en lecture :
        ofi =askopenfile(filetypes=[("Texte",".txt"),("Tous","*")])
        lignes = ofi.readlines()
        for li in lignes:
            cv = li.split() # extraction de la clé et la valeur corresp.
            self.dico[cv[0]] = cv[1]
            ofi.close()
        if __name__ == '__main__':
            Application().mainloop()

Exercice 13.23 (variante 3) :

from tkinter import *
from random import randrange

from math import sin, cos, pi
class FaceDom(object):
    def __init__(self, can, val, pos, taille =70):
        self.can =can
        x, y, c = pos[0], pos[1], taille/2
        self. carre = can.create_rectangle(x -c, y-c, x+c, y+c,
        fill ='ivory', width =2)
        d = taille/3
        # disposition des points sur la face, pour chacun des 6 cas :
        self.pDispo = [((0,0),),
                ((-d,d),(d,-d)),
                ((-d,-d), (0,0), (d,d)),
                ((-d,-d),(-d,d),(d,-d),(d,d)),
                ((-d,-d),(-d,d),(d,-d),(d,d),(0,0)),
                ((-d,-d),(-d,d),(d,-d),(d,d),(d,0),(-d,0))]

        self.x, self.y, self.dim = x, y, taille/15
        self.pList =[] # liste contenant les points de cette face
        self.tracer_points(val)

    def tracer_points(self, val):
         # créer les dessins de points correspondant à la valeur val :
        disp = self.pDispo[val -1]
        for p in disp:
            self.cercle(self.x +p[0], self.y +p[1], self.dim, 'red')
            self.val = val

    def cercle(self, x, y, r, coul):
        self.pList.append(self.can.create_oval(x-r, y-r, x+r, y+r, fill=coul))

    def effacer(self, flag =0):
        for p in self.pList:
            self.can.delete(p)
            if flag:
                self.can.delete(self.carre)

class Projet(Frame):
    def __init__(self, larg, haut):
        Frame.__init__(self)
        self.larg, self.haut = larg, haut
        self.can = Canvas(self, bg='dark green', width =larg, height =haut)
        self.can.pack(padx =5, pady =5)
        # liste des boutons à installer, avec leur gestionnaire :
        bList = [("A", self.boutA), ("B", self.boutB),
        ("C", self.boutC), ("Quitter", self.boutQuit)]
        bList.reverse() # inverser l'ordre de la liste
        for b in bList:
            Button(self, text =b[0], command =b[1]).pack(side =RIGHT, padx=3)
            self.pack()
            self.des =[] # liste qui contiendra les faces de dés
            self.actu =0 # réf. du dé actuellement sélectionné

    def boutA(self):
        if len(self.des):
            return # car les dessins existent déjà !
        a, da = 0, 2*pi/13
        for i in range(13):
            cx, cy = self.larg/2, self.haut/2
            x = cx + cx*0.75*sin(a) # pour disposer en cercle,
            y = cy + cy*0.75*cos(a) # on utilise la trigono !
            self.des.append(FaceDom(self.can, randrange(1,7) , (x,y), 65))
            a += da
    def boutB(self):
        # incrémenter la valeur du dé sélectionné. Passer au suivant :
        v = self.des[self.actu].val
        v = v % 6
        v += 1
        self.des[self.actu].effacer()
        self.des[self.actu].tracer_points(v)
        self.actu += 1
        self.actu = self.actu % 13
        def boutC(self):
        for i in range(len(self.des)):
            self.des[i].effacer(1)
            self.des =[]
            self.actu =0

    def boutQuit(self):
        self.master.destroy()

Projet(600, 600).mainloop()