Python, Instructions répétitives

Python

Pour les Exercices (La solution des Exercices sont à la fin de la page)

L’une des tâches que les machines font le mieux est la répétition sans erreur de tâches identiques. Il existe bien des méthodes pour programmer ces tâches répétitives. Nous allons commencer par l’une des plus fondamentales : la boucle de répétition construite autour de l’instruction while.

Réaffectation

Nous ne l’avions pas encore signalé explicitement : il est permis de réaffecter une nouvelle valeur à une même variable, autant de fois qu’on le souhaite.

L’effet d’une réaffectation est de remplacer l’ancienne valeur d’une variable par une nouvelle.

>>> altitude = 320
>>> print(altitude)
320
>>> altitude = 375
>>> print(altitude)
375

Ceci nous amène à attirer une nouvelle fois votre attention sur le fait que le symbole égale utilisé sous Python pour réaliser une affectation ne doit en aucun cas être confondu avec un symbole d’égalité tel qu’il est compris en mathématique. Il est tentant d’interpréter l’instruction altitude = 320 comme une affirmation d’égalité, mais ce n’en est pas une !

• Premièrement, l’égalité est commutative, alors que l’affectation ne l’est pas. Ainsi, en mathématique, les écritures a = 7 et 7 = a sont équivalentes, alors qu’une instruction de programmation telle que 375 = altitude serait illégale.

• Deuxièmement, l’égalité est permanente, alors que l’affectation peut être remplacée comme nous venons de le voir. Lorsqu’en mathématique, nous affirmons une égalité telle que a = b au début d’un raisonnement, alors a continue à être égal à b durant tout le développement qui suit.

En programmation, une première instruction d’affectation peut rendre égales les valeurs de deux variables, et une instruction ultérieure en changer ensuite l’une ou l’autre.

Exemple :

>>> a = 5
>>> b = a # a et b contiennent des valeurs égales
>>> b = 2 # a et b sont maintenant différentes

Rappelons ici que Python permet d’affecter leurs valeurs à plusieurs variables simultanément :

>>> a, b, c, d = 3, 4, 5, 7

Cette fonctionnalité de Python est bien plus intéressante encore qu’elle n’en a l’air à première vue. Supposons par exemple que nous voulions maintenant échanger les valeurs des variables a et c (actuellement, a contient la valeur 3, et c la valeur 5 ; nous voudrions que ce soit l’inverse).

Comment faire ?

Exercice

4.1 Écrivez les lignes d’instructions nécessaires pour obtenir ce résultat.

À la suite de l’exercice proposé ci-dessus, vous aurez certainement trouvé une méthode, et un professeur vous demanderait certainement de la commenter en classe.

Comme il s’agit d’une opération courante, les langages de programmation proposent souvent des raccourcis pour l’effectuer (par exemple des instructions spécialisées, telle l’instruction SWAP du langage Basic).

Sous Python, l’affectation parallèle permet de programmer l’échange d’une manière particulièrement élégante :

>>> a, b = b, a

(On pourrait bien entendu échanger d’autres variables en même temps, dans la même instruction.)

Répétitions en boucle – L’instruction while

En programmation, on appelle boucle un système d’instructions qui permet de répéter un certain nombre de fois (voire indéfiniment) toute une série d’opérations.

Python propose deux instructions particulières pour construire des boucles :

l’instruction for … in … , très puissante, que nous étudierons plus loins, et l’instruction while que nous allons découvrir tout de suite.

Veuillez donc entrer les commandes ci-dessous :

>>> a = 0
>>> while (a < 7): # (n’oubliez pas le double point !)
... a = a + 1 # (n’oubliez pas l’indentation !)
... print(a)

Frappez encore une fois <Enter>.

Que se passe-t-il ?

Avant de lire les commentaires de la page suivante, prenez le temps d’ouvrir votre cahier et d’y noter cette série de commandes. Décrivez aussi le résultat obtenu, et essayez de l’expliquer de la manière la plus détaillée possible.
Commentaires

Le mot while signifie « tant que » en anglais. Cette instruction utilisée à la seconde ligne indique à Python qu’il lui faut répéter continuellement le bloc d’instructions qui suit, tant que le contenu de la variable a reste inférieur à 7.

Comme l’instruction if abordée au chapitre précédent, l’instruction while amorce une instruction composée. Le double point à la fin de la ligne introduit le bloc d’instructions à répéter, lequel doit obligatoirement se trouver en retrait.

Comme vous l’avez appris au chapitre précédent, toutes les instructions d’un même bloc doivent être indentées exactement au même niveau (c’est-à-dire décalées à droite d’un même nombre d’espaces).

Nous avons ainsi construit notre première boucle de programmation, laquelle répète un certain nombre de fois le bloc d’instructions indentées. Voici comment cela fonctionne :

• Avec l’instruction while, Python commence par évaluer la validité de la condition fournie entre parenthèses (celles-ci sont optionnelles, nous ne les avons utilisées que pour clarifier notre explication).

• Si la condition se révèle fausse, alors tout le bloc qui suit est ignoré et l’exécution du programme se termine14.

• Si la codition est vraie, alors Python exécute tout le bloc d’instructions constituant le corps de la boucle, c’est-à-dire :
– l’instruction a = a + 1 qui incrémente d’une unité le contenu de la variable a (ce qui signifie que l’on affecte à la variable a une nouvelle valeur, qui est égale à la valeur précédente augmentée d’une unité).

– l’appel de la fonction print() pour afficher la valeur courante de la variable a.

• lorsque ces deux instructions ont été exécutées, nous avons assisté à une première itération, et le programme boucle, c’est-à-dire que l’exécution reprend à la ligne contenant l’instruction while.

La condition qui s’y trouve est à nouveau évaluée, et ainsi de suite.

Dans notre exemple, si la condition a < 7 est encore vraie, le corps de la boucle est exécuté une nouvelle fois et le bouclage se poursuit.

Remarques

• La variable évaluée dans la condition doit exister au préalable (il faut qu’on lui ait déjà affecté au moins une valeur).

• Si la condition est fausse au départ, le corps de la boucle n’est jamais exécuté.

• Si la condition reste toujours vraie, alors le corps de la boucle est répété indéfiniment (tout au moins tant que Python lui-même continue à fonctionner).

Il faut donc veiller à ce que le corps de la boucle contienne au moins une instruction qui change la valeur d’une variable intervenant dans la condition évaluée par while, de manière à ce que cette condition puisse devenir fausse et la boucle se terminer.

Exemple de boucle sans fin (à éviter !) :

>>> n = 3
>>> while n < 5:
... print("hello !")

Élaboration de tables

Recommencez à présent le premier exercice, mais avec la petite modification ci-dessous :

>>> a = 0
>>> while a < 12:
... a = a +1
... print(a , a**2 , a**3)

Vous devriez obtenir la liste des carrés et des cubes des nombres de 1 à 12.

Notez au passage que la fonction print() permet d’afficher plusieurs expressions l’une à la suite de l’autre sur la même ligne : il suffit de les séparer par des virgules. Python insère automatiquement un espace entre les éléments affichés.

Construction d’une suite mathématique

Le petit programme ci-dessous permet d’afficher les dix premiers termes d’une suite appelée « Suite de Fibonacci ». Il s’agit d’une suite de nombres dont chaque terme est égal à la somme des deux termes qui le précèdent. Analysez ce programme (qui utilise judicieusement l’affectation parallèle) et décrivez le mieux possible le rôle de chacune des instructions.

>>> a, b, c = 1, 1, 1
>>> while c < 11 :
... print(b, end =" ")
... a, b, c = b, a+b, c+1


Lorsque vous lancez l’exécution de ce programme, vous obtenez :

1 2 3 5 8 13 21 34 55 89

Les termes de la suite de Fibonacci sont affichés sur la même ligne. Vous obtenez ce résultat grâce au second argument end =" " fourni à la fonction print().

Par défaut, la fonction print() ajoute en effet un caractère de saut à la ligne à toute valeur qu’on lui demande d’afficher.

L’argument end =" " signifie que vous souhaitez remplacer le saut à la ligne par un simple espace. Si vous supprimez cet argument, les nombres seront affichés les uns en-dessous des autres.

Dans vos programmes futurs, vous serez très souvent amenés à mettre au point des boucles de répétition comme celle que nous analysons ici. Il s’agit d’une question essentielle, que vous devez apprendre à maîtriser parfaitement.

Soyez sûr que vous y arriverez progressivement, à force d’exercices. Lorsque vous examinez un problème de cette nature, vous devez considérer les lignes d’instruction, bien entendu, mais surtout décortiquer les états successifs des différentes variables impliquées dans la boucle.

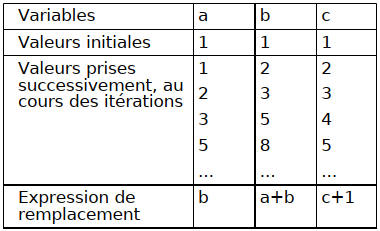
Cela n’est pas toujours facile, loin de là. Pour vous aider à y voir plus clair, prenez la peine de dessiner sur papier une table d’états similaire à celle que nous reproduisons ci-dessous pour notre programme « suite de Fibonacci » :

Dans une telle table, on effectue en quelque sorte « à la main » le travail de l’ordinateur, en indiquant ligne par ligne les valeurs que prendront chacune des variables au fur et à mesure des itérations successives.

On commence par inscrire en haut du tableau les noms des variables concernées. Sur la ligne suivante, les valeurs initiales de ces variables (valeurs qu’elles possèdent avant le démarrage de la boucle). Enfin, tout en bas du tableau, les expressions utilisées dans la boucle pour modifier l’état de chaque variable à chaque itération.

On remplit alors quelques lignes correspondant aux premières itérations. Pour établir les valeurs d’une ligne, il suffit d’appliquer à celles de la ligne précédente, l’expression de remplacement qui se trouve en bas de chaque colonne.

On vérifie ainsi que l’on obtient bien la suite recherchée. Si ce n’est pas le cas, il faut essayer d’autres expressions de remplacement.

Exercices

4.2 Écrivez un programme qui affiche les 20 premiers termes de la table de multiplication par 7.

4.3 Écrivez un programme qui affiche une table de conversion de sommes d’argent exprimées en euros, en dollars canadiens. La progression des sommes de la table sera « géométrique », comme dans l’exemple ci-dessous :

1 euro(s) = 1.65 dollar(s)
2 euro(s) = 3.30 dollar(s)
4 euro(s) = 6.60 dollar(s)
8 euro(s) = 13.20 dollar(s)
etc. (S’arrêter à 16384 euros.)

4.4 Écrivez un programme qui affiche une suite de 12 nombres dont chaque terme soit égal au triple du terme précédent.

Premiers scripts, ou comment conserver nos programmes

Exercices

4.5 Écrivez un programme qui calcule le volume d’un parallélépipède rectangle dont sont fournis au départ la largeur, la hauteur et la profondeur.

4.6 Écrivez un programme qui convertit un nombre entier de secondes fourni au départ en un nombre d’années, de mois, de jours, de minutes et de secondes (utilisez l’opérateur modulo : % ).

4.7 Écrivez un programme qui affiche les 20 premiers termes de la table de multiplication par 7, en signalant au passage (à l’aide d’une astérisque) ceux qui sont des multiples de 3. Exemple : 7 14 21 * 28 35 42 * 49 ...

4.8 Écrivez un programme qui calcule les 50 premiers termes de la table de multiplication par 13, mais n’affiche que ceux qui sont des multiples de 7.

4.9 Écrivez un programme qui affiche la suite de symboles suivante :

*
**
***
****
*****
******
*******

Solutions des exercices

Exercice 4.2 :
>>> c = 0
>>> while c < 20:
... c = c +1
... print(c, "x 7 =", c*7)

ou encore :
>>> c = 1
>>> while c <= 20:
... print(c, "x 7 =", c*7)
... c = c +1

Exercice 4.3 :
>>> s = 1
>>> while s <= 16384:
... print(s, "euro(s) =", s *1.65, "dollar(s)")
... s = s *2

Exercice 4.4 :
>>> a, c = 1, 1
>>> while c < 13:
... print(a, end =’ ‘)
... a, c = a *3, c+1

Exercice 4.6 :
# Le nombre de secondes est fourni au départ :
# (un grand nombre s'impose !) nsd = 12345678912

# Nombre de secondes dans une journée : nspj = 3600 * 24

# Nombre de secondes dans un an (soit 365 jours -
# on ne tiendra pas compte des années bissextiles) :
nspa = nspj * 365

# Nombre de secondes dans un mois (en admettant
# pour chaque mois une durée identique de 30 jours) :
nspm = nspj * 30

# Nombre d'années contenues dans la durée fournie :
na = nsd // nspa # division <entière>
nsr = nsd % nspa # n. de sec. restantes

# Nombre de mois restants :
nmo = nsr // nspm # division <entière>
nsr = nsr % nspm # n. de sec. restantes

# Nombre de jours restants :
nj = nsr // nspj # division <entière>
nsr = nsr % nspj # n. de sec. restantes

# Nombre d'heures restantes :
nh = nsr // 3600 # division <entière>
nsr = nsr % 3600 # n. de sec. restantes

# Nombre de minutes restantes :
nmi = nsr // 60 # division <entière>
nsr = nsr % 60 # n. de sec. restantes
print("Nombre de secondes à convertir :", nsd)
print("Cette durée correspond à", na, "années de 365 jours, plus")
print(nmo, "mois de 30 jours,", end=' ')
print(nj, "jours,", end=' ')
print(nh, "heures,", end=' ')
print(nmi, "minutes et", end=' ')
print(nsr, "secondes.")

Exercice 4.7 :
# affichage des 20 premiers termes de la table par 7,
# avec signalement des multiples de 3 :
i = 1 # compteur : prendra successivement les valeurs de 1 à 20
while i < 21:
# calcul du terme à afficher :
t = i * 7

# affichage sans saut à la ligne (utilisation de la virgule) :
print(t, end =’ ‘)

# ce terme est-il un multiple de 3 ? (utilisation de l'opérateur modulo) :
if t % 3 == 0:
print("*", end =’ ‘) # affichage d'une astérisque dans ce cas
i = i + 1 # incrémentation du compteur dans tous les cas