Utilisation de fenêtres et de graphismes

Python

Jusqu’à présent, nous avons utilisé Python exclusivement « en mode texte ». Nous avons procédé ainsi parce qu’il nous fallait absolument d’abord dégager un certain nombre de concepts élémentaires ainsi que la structure de base du langage, avant d’envisager des expériences impliquant des objets informatiques plus élaborés (fenêtres, images, sons, etc.).

Nous pouvons maintenant nous permettre une petite incursion dans le vaste domaine des interfaces graphiques, mais ce ne sera qu’un premier amuse-gueule : il nous reste en effet encore bien des choses fondamentales à apprendre, et pour nombre d’entre elles l’approche textuelle reste la plus abordable.

Interfaces graphiques (GUI) Si vous ne le saviez pas encore, apprenez dès à présent que le domaine des interfaces graphiques (ou GUI, Graphical User Interfaces) est extrêmement complexe.

Chaque système d’exploitation peut en effet proposer plusieurs « bibliothèques » de fonctions graphiques de base, auxquelles viennent fréquemment s’ajouter de nombreux compléments, plus ou moins spécifiques de langages de programmation particuliers. Tous ces composants sont généralement présentés comme des classes d’objets, dont il vous faudra étudier les attributs et les méthodes.

Avec Python, la bibliothèque graphique la plus utilisée jusqu’à présent est la bibliothèque tkinter, qui est une adaptation de la bibliothèque Tk développée à l’origine pour le langage Tcl. Plusieurs autres bibliothèques graphiques fort intéressantes ont été proposées pour Python : wxPython, pyQT, pyGTK, etc.

Il existe également des possibilités d’utiliser les bibliothèques de widgets Java et les MFC de Win- dows. Dans le cadre de ces notes, nous nous limiterons cependant à tkinter, dont il existe fort heureusement des versions similaires (et gratuites) pour les plates-formes Linux, Windows et Mac OS.

Premiers pas avec tkinter

Pour la suite des explications, nous supposerons bien évidemment que le module tkinter a déjà été installé sur votre système. Pour pouvoir en utiliser les fonctionnalités dans un script Python, il faut que l’une des premières lignes de ce script contienne l’instruction d’importation :

from tkinter import *

Comme toujours sous Python, il n’est même pas nécessaire d’écrire un script. Vous pouvez faire un grand nombre d’expériences directement à la ligne de commande, en ayant simplement lancé Python en mode interactif.

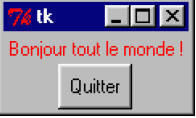
Dans l’exemple qui suit, nous allons créer une fenêtre très simple, et y ajouter deux widgets typiques : un bout de texte (ou label) et un bouton (ou button).

>>> from tkinter import *
>>> fen1 = Tk()
>>> tex1 = Label(fen1, text='Bonjour tout le monde !', fg='red')
>>> tex1.pack()
>>> bou1 = Button(fen1, text='Quitter', command = fen1.destroy)
>>> bou1.pack()
>>> fen1.mainloop()

Suivant la version de Python utilisée, vous verrez déjà apparaître la fenêtre d’application immédiatement après avoir entré la deuxième commande de cet exemple, ou bien seulement après la septième.

Examinons à présent plus en détail chacune des lignes de commandes exécutées

1. Comme cela a déjà été expliqué précédemment, il est aisé de construire différents modules Python, qui contiendront des scripts, des définitions de fonctions, des classes d’objets, etc.

On peut alors importer tout ou partie de ces modules dans n’importe quel programme, ou même dans l’interpréteur fonctionnant en mode interactif (c’est-à-dire directement à la ligne de commande). C’est ce que nous faisons à la première ligne de notre exemple : from tkinter import * consiste à importer toutes les classes contenues dans le module tkinter.

Nous devrons de plus en plus souvent parler de ces classes. En programmation, on appelle ainsi des générateurs d’objets, lesquels sont eux-mêmes des morceaux de programmes réutilisables. Nous n’allons pas essayer de vous fournir dès à présent une définition définitive et précise de ce que sont les objets et les classes, mais plutôt vous proposer d’en utiliser directement quelques-un(e)s. Nous affinerons notre compréhension petit à petit par la suite.

2. À la deuxième ligne de notre exemple : fen1 = Tk(), nous utilisons l’une des classes du module tkinter, la classe Tk(), et nous en créons une instance (autre terme désignant un objet spécifique), à savoir la fenêtre fen1.

Ce processus d’instanciation d’un objet à partir d’une classe est une opération fondamentale dans les techniques actuelles de programmation. Celles-ci font en effet de plus en plus souvent appel à une méthodologie que l’on appelle programmation orientée objet (ou OOP : Object Oriented Programming).

La classe est en quelque sorte un modèle général (ou un moule) à partir duquel on demande à la machine de construire un objet informatique particulier. La classe contient toute une série de définitions et d’options diverses, dont nous n’utilisons qu’une partie dans l’objet que nous créons à partir d’elle.

Ainsi la classe Tk(), qui est l’une des classes les plus fondamentales de la bibliothèque tkinter, contient tout ce qu’il faut pour engendrer différents types de fenêtres d’application, de tailles ou de couleurs diverses, avec ou sans barre de menus, etc.

Nous nous en servons ici pour créer notre objet graphique de base, à savoir la fenêtre qui contiendra tout le reste. Dans les parenthèses de Tk(), nous pourrions préciser différentes options, mais nous laisserons cela pour un peu plus tard.

L’instruction d’instanciation ressemble à une simple affectation de variable. Comprenons bien cependant qu’il se passe ici deux choses à la fois :

○ la création d’un nouvel objet, (lequel peut être fort complexe dans certains cas, et par conséquent occuper un espace mémoire considérable) ;

○ l’affectation d’une variable, qui va désormais servir de référence pour manipuler l’objet.

3. À la troisième ligne :

tex1 = Label(fen1, text='Bonjour tout le monde !', fg='red'),

nous créons un autre objet (un widget), cette fois à partir de la classe Label(). Comme son nom l’indique, cette classe définit toutes sortes d’étiquettes (ou de libellés).

En fait, il s’agit tout simplement de fragments de texte quelconques, utilisables pour afficher des informations et des messages divers à l’intérieur d’une fenêtre. Nous efforçant d’apprendre au passage la manière correcte d’exprimer les choses, nous dirons que nous créons ici l’objet tex1 par instanciation de la classe Label().

Remarquons que nous faisons appel à une classe, de la même manière que nous faisons appel à une fonction : c’est-à-dire en fournissant un certain nombre d’arguments dans des parenthèses. Nous verrons plus loin qu’une classe est en fait une sorte de « conteneur » dans lequel sont regroupées des fonctions et des données. Quels arguments avons-nous donc fournis pour cette instanciation ?

○ Le premier argument transmis (fen1), indique que le nouveau widget que nous sommes en train de créer sera contenu dans un autre widget préexistant, que nous désignons donc ici comme son « maître » : l’objet fen1 est le widget maître de l’objet tex1. On pourra dire aussi que l’objet tex1 est un widget esclave de l’objet fen1.

○ Les deux arguments suivants servent à préciser la forme exacte que doit prendre notre widget. Ce sont en effet deux options de création, chacune fournie sous la forme d’une chaîne de caractères : d’abord le texte de l’étiquette, ensuite sa couleur d’avant-plan (ou foreground, en abrégé fg).

Ainsi le texte que nous voulons afficher est bien défini, et il doit apparaître coloré en rouge. Nous pourrions encore préciser bien d’autres caractéristiques : la police à utiliser, ou la couleur d’arrière-plan, par exemple.

Toutes ces caractéristiques ont cependant une valeur par défaut dans les définitions internes de la classe Label(). Nous ne devons indiquer des options que pour les caractéristiques que nous souhaitons différentes du modèle standard.

4. À la quatrième ligne de notre exemple : tex1.pack(), nous activons une méthode associée à l’objet tex1 : la méthode pack().

Nous avons déjà rencontré ce terme de méthode (à propos des listes, notamment). Une méthode est une fonction intégrée à un objet (on dira aussi qu’elle est encapsulée dans l’objet). Nous apprendrons bientôt qu’un objet informatique est en fait un élément de programme contenant toujours :

○ un certain nombre de données (numériques ou autres), contenues dans des variables de types divers : on les appelle les attributs (ou les propriétés) de l’objet ;

○ un certain nombre de procédures ou de fonctions (qui sont donc des algorithmes) : on les appelle les méthodes de l’objet.

La méthode pack() fait partie d’un ensemble de méthodes qui sont applicables non seulement aux widgets de la classe Label(), mais aussi à la plupart des autres widgets tkinter, et qui agissent sur leur disposition géométrique dans la fenêtre. Comme vous pouvez le constater par vous-même si vous entrez les commandes de notre exemple une par une, la méthode pack() réduit automatiquement la taille de la fenêtre « maître » afin qu’elle soit juste assez grande pour contenir les widgets « esclaves » définis au préalable.

5. À la cinquième ligne : bou1 = Button(fen1, text=’Quitter’, command = fen1.destroy), nous créons notre second widget « esclave » : un bouton.

Comme nous l’avons fait pour le widget précédent, nous appelons la classe Button() en fournissant entre parenthèses un certain nombre d’arguments. Étant donné qu’il s’agit cette fois d’un objet interactif, nous devons préciser avec l’option command ce qui devra se passer lorsque l’utilisateur effectuera un clic sur le bouton.

Dans ce cas précis, nous actionnerons la méthode destroy associée à l’objet fen1, ce qui devrait provoquer l’effacement de la fenêtre.

6. La sixième ligne utilise la méthode pack() pour adapter la géométrie de la fenêtre au nouvel objet que nous venons d’y intégrer.

7. La septième ligne : fen1.mainloop() est très importante, parce que c’est elle qui provoque le démarrage du réceptionnaire d’événements associé à la fenêtre.

Cette instruction est nécessaire pour que notre application soit « à l’affût » des clics de souris, des pressions exercées sur les touches du clavier, etc.

C’est donc cette instruction qui « la met en marche », en quelque sorte. Comme son nom l’indique (mainloop), il s’agit d’une méthode de l’objet fen1, qui active une boucle de programme, laquelle « tournera » en permanence en tâche de fond, dans l’attente de messages émis par le système d’exploitation de l’ordinateur.

Celui-ci interroge en effet sans cesse son environnement, notamment au niveau des périphériques d’entrée (souris, clavier, etc.). Lorsqu’un évènement quelconque est détecté, divers messages décrivant cet évènement sont expédiés aux programmes qui souhaitent en être avertis. Voyons cela un peu plus en détail.

Programmes pilotés par des évènements

Vous venez d’expérimenter votre premier programme utilisant une interface graphique. Ce type de programme est structuré d’une manière différente des scripts « textuels » étudiés auparavant.

Tous les programmes d’ordinateur comportent grosso-modo trois phases principales :

une phase d’initialisation, laquelle contient les instructions qui préparent le travail à effectuer (appel des modules externes nécessaires, ouverture de fichiers, connexion à un serveur de bases de données ou à l’Inter- net, etc.),

une phase centrale où l’on trouve la véritable fonctionnalité du programme (c’est-à-dire tout ce qu’il est censé faire : afficher des données à l’écran, effectuer des calculs, modifier le contenu d’un fichier, imprimer, etc.),

et enfin une phase de terminaison qui sert à clôturer « proprement » les opérations (c’est-à-dire fermer les fichiers restés ouverts, couper les connexions externes, etc.).

Dans un programme « en mode texte », ces trois phases sont simplement organisées suivant un schéma linéaire comme dans l’illustration ci-contre.

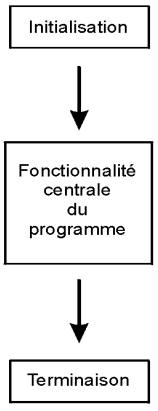
En conséquence, ces programmes se caractérisent par une interactivité très limitée avec l’utilisateur. Celui-ci ne dispose pratiquement d’aucune liberté : il lui est demandé de temps à autre d’entrer des données au clavier, mais toujours dans un ordre prédéterminé correspondant à la séquence d’instructions du programme. Dans le cas d’un programme qui utilise une interface graphique, par contre, l’organisation interne est différente. On dit d’un tel programme qu’il est piloté par les évènements.

Après sa phase d’initialisation, un programme de ce type se met en quelque sorte « en attente », et passe la main à un autre logiciel, lequel est plus ou moins intimement intégré au système d’exploitation de l’ordinateur et « tourne » en permanence.

Ce réceptionnaire d’évènements scrute sans cesse tous les périphériques (clavier, souris, horloge, modem, etc.) et réagit immédiatement lorsqu’un évènement y est détecté. Un tel évènement peut être une action quelconque de l’utilisateur : déplacement de la souris, appui sur une touche, etc., mais aussi un évènement externe ou un automatisme (top d’horloge, par exemple).

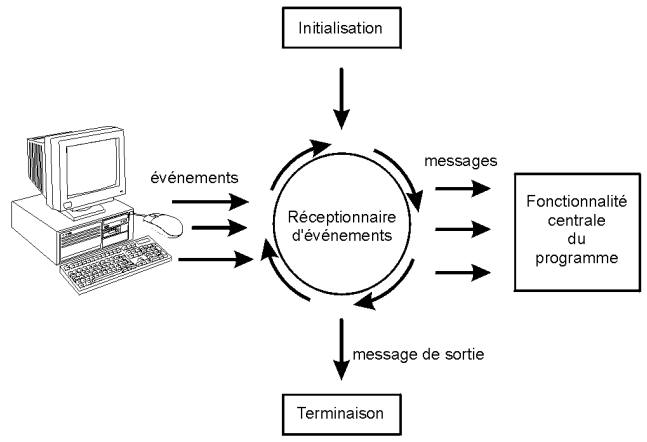
Lorsqu’il détecte un évènement, le réceptionnaire envoie un message spécifique au programme, lequel doit être conçu pour réagir en conséquence. La phase d’initialisation d’un programme utilisant une interface graphique comporte un ensemble d’instructions qui mettent en place les divers composants interactifs de cette interface (fenêtres, boutons, cases à cocher, etc.).

D’autres instructions définissent les messages d’évènements qui devront être pris en charge : on peut en effet décider que le programme ne réagira qu’à certains évènements en ignorant tous les autres.

Alors que dans un programme « textuel », la phase centrale est constituée d’une suite d’instructions qui décrivent à l’avance l’ordre dans lequel la machine devra exécuter ses différentes tâches (même s’il est prévu des cheminements différents en réponse à certaines conditions rencontrées en cours de route), on ne trouve dans la phase centrale d’un programme avec interface graphique qu’un ensemble de fonctions indépendantes.

Chacune de ces fonctions est appelée spécifiquement lorsqu’un évènement particulier est détecté par le système d’exploitation : elle effectue alors le travail que l’on attend du programme en réponse à cet évènement, et rien d’autre. Il est important de bien comprendre ici que pendant tout ce temps, le réceptionnaire continue à « tourner » et à guetter l’apparition d’autres évènements éventuels.

S’il arrive d’autres évènements, il peut donc se faire qu’une deuxième fonction (ou une 3e, une 4e...) soit activée et commence à effectuer son travail « en parallèle » avec la première qui n’a pas encore terminé le sien.

Les systèmes d’exploitation et les langages modernes permettent en effet ce parallélisme que l’on appelle aussi multitâche. Au chapitre précédent, nous avons déjà remarqué que la structure du texte d’un programme n’indique pas directement l’ordre dans lequel les instructions seront finalement exécutées.

Cette remarque s’applique encore bien davantage dans le cas d’un programme avec interface graphique, puisque l’ordre dans lequel les fonctions sont appelées n’est plus inscrit nulle part dans le programme. Ce sont les évènements qui pilotent ! Tout ceci doit vous paraître un peu compliqué. Nous allons l’illustrer dans quelques exemples.

Exemple graphique : tracé de lignes dans un canevas

Le script décrit ci-dessous crée une fenêtre comportant trois boutons et un canevas.

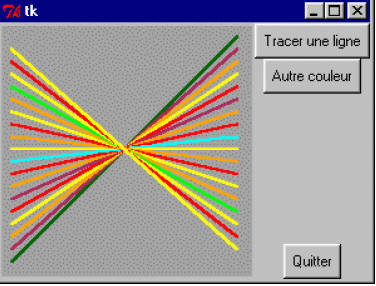
Suivant la terminologie de tkinter, un canevas est une surface rectangulaire délimitée, dans laquelle on peut installer ensuite divers dessins et images à l’aide de méthodes spécifiques. Lorsque l’on clique sur le bouton <Tracer une ligne>, une nouvelle ligne colorée apparaît sur le canevas, avec à chaque fois une inclinaison différente de la précédente.

Si l’on actionne le bouton <Autre couleur>, une nouvelle couleur est tirée au hasard dans une série limitée. Cette couleur est celle qui s’appliquera aux tracés suivants. Le bouton <Quitter> sert bien évidemment à terminer l’application en refermant la fenêtre.

# Petit exercice utilisant la bibliothèque graphique tkinter
from tkinter import *
from random import randrange

# --- définition des fonctions gestionnaires d'événements : ---
def drawline():
    "Tracé d'une ligne dans le canevas can1"
    global x1, y1, x2, y2, coul
    can1.create_line(x1,y1,x2,y2,width=2,fill=coul)

# modification des coordonnées pour la ligne suivante :
    y2, y1 = y2+10, y1-10
def changecolor():
    "Changement aléatoire de la couleur du tracé"
    global coul
    pal=['purple','cyan','maroon','green','red','blue','orange','yellow']
    c = randrange(8) # => génère un nombre aléatoire de 0 à 7
    coul = pal[c]

#------ Programme principal -------

# les variables suivantes seront utilisées de manière globale :

x1, y1, x2, y2 = 10, 190, 190, 10 # coordonnées de la ligne
coul = 'dark green' # couleur de la ligne

# Création du widget principal ("maître") :
fen1 = Tk()

# création des widgets "esclaves" :
can1 = Canvas(fen1,bg='dark grey',height=200,width=200)
can1.pack(side=LEFT)
bou1 = Button(fen1,text='Quitter',command=fen1.quit)
bou1.pack(side=BOTTOM)
bou2 = Button(fen1,text='Tracer une ligne',command=drawline)
bou2.pack()
bou3 = Button(fen1,text='Autre couleur',command=changecolor)
bou3.pack()

fen1.mainloop() # démarrage du réceptionnaire d’évènements
fen1.destroy() # destruction (fermeture) de la fenêtre

Conformément à ce que nous avons expliqué dans le texte des pages précédentes, la fonctionnalité de ce programme est essentiellement assurée par les deux fonctions drawline() et changecolor(), qui seront activées par des évènements, ceux-ci étant eux-mêmes définis dans la phase d’initialisation.

Dans cette phase d’initialisation, on commence par importer l’intégralité du module tkinter ainsi qu’une fonction du module random qui permet de tirer des nombres au hasard. On crée ensuite les différents widgets par instanciation à partir des classes Tk(), Canvas() et Button().

Remarquons au passage que la même classe Button() sert à instancier plusieurs boutons, qui sont des objets similaires pour l’essentiel, mais néanmoins individualisés grâce aux options de création et qui pourront fonctionner indépendamment l’un de l’autre. L’initialisation se termine avec l’instruction fen1.mainloop() qui démarre le réceptionnaire d’évènements.

Les instructions qui suivent ne seront exécutées qu’à la sortie de cette boucle, sortie elle-même déclenchée par la méthode fen1.quit() (voir ci-après).

L’option command utilisée dans l’instruction d’instanciation des boutons permet de désigner la fonction qui devra être appelée lorsqu’un évènement « clic gauche de la souris sur le widget » se produira. Il s’agit en fait d’un raccourci pour cet évènement particulier, qui vous est proposé par tkinter pour votre facilité parce que cet évènement est celui que l’on associe naturellement à un widget de type bouton.

Nous verrons plus loin qu’il existe d’autres techniques plus générales pour associer n’importe quel type d’évènement à n’importe quel widget. Les fonctions de ce script peuvent modifier les valeurs de certaines variables qui ont été définies au niveau principal du programme. Cela est rendu possible grâce à l’instruction global utilisée dans la définition de ces fonctions.

Nous nous permettrons de procéder ainsi pendant quelque temps encore (ne serait-ce que pour vous habituer à distinguer les comportements des variables locales et globales), mais comme vous le comprendrez plus loin, cette pratique n’est pas vraiment recommandable, surtout lors qu’il s’agit d’écrire de grands programmes.

Nous apprendrons une meilleure technique lorsque nous aborderons l’étude des classes (à partir de la page 163). Dans notre fonction changecolor(), une couleur est choisie au hasard dans une liste. Nous utilisons pour ce faire la fonction randrange() importée du module random.

Appelée avec un argument N, cette fonction renvoie un nombre entier, tiré au hasard entre 0 et N-1. La commande liée au bouton <Quitter> appelle la méthode quit() de la fenêtre fen1. Cette méthode sert à fermer (quitter) le réceptionnaire d’évènements (mainloop) associé à cette fenêtre.

Lorsque cette méthode est activée, l’exécution du programme se poursuit avec les instructions qui suivent l’appel de mainloop. Dans notre exemple, cela consiste donc à effacer (destroy) la fenêtre.

Exercices

Les solutions des exercices se trouve à la fin de la page.

8.1 Comment faut-il modifier le programme pour ne plus avoir que des lignes de couleur cyan, maroon et green ?

8.2 Comment modifier le programme pour que toutes les lignes tracées soient horizontales et parallèles ?

8.3 Agrandissez le canevas de manière à lui donner une largeur de 500 unités et une hauteur de 650. Modifiez également la taille des lignes, afin que leurs extrémités se confondent avec les bords du canevas.

8.4 Ajoutez une fonction drawli ne2 qui tracera deux lignes rouges en croix au centre du canevas : l’une horizontale et l’autre verticale. Ajoutez également un bouton portant l’indica- tion « viseur ». Un clic sur ce bouton devra provoquer l’affichage de la croix.

8.5 Reprenez le programme initial. Remplacez la méthode create_line par create_rectangle. Que se passe-t-il ? De la même façon, essayez aussi create_arc, create_oval, et create_polygon. Pour chacune de ces méthodes, notez ce qu’indiquent les coordonnées fournies en paramètres. (Remarque : pour le polygone, il est nécessaire de modifier légèrement le programme !)

8.6 - Supprimez la ligne global x1, y1, x2, y2 dans la fonction drawline du programme original. Que se passe-t-il ? Pourquoi ? - Si vous placez plutôt « x1, y1, x2, y2 » entre les parenthèses, dans la ligne de définition de la fonction drawline, de manière à transmettre ces variables à la fonction en tant que paramètres, le programme fonctionne-t-il encore ? N’oubliez pas de modifier aussi la ligne du programme qui fait appel à cette fonction ! - Si vous définissez x1, y1, x2, y2 = 10, 390, 390, 10 à la place de global x1, y1..., que se passe-t-il ? Pourquoi ? Quelle conclusion pouvez-vous tirer de tout cela ?

8.7 a) Créez un court programme qui dessinera les 5 anneaux olympiques dans un rectangle de fond blanc (white). Un bouton <Quitter> doit permettre de fermer la fenêtre. b) Modifiez le programme ci-dessus en y ajoutant 5 boutons. Chacun de ces boutons provoquera le tracé de chacun des 5 anneaux

8.8 Dans votre cahier de notes, établissez un tableau à deux colonnes. Vous y noterez à gauche les définitions des classes d’objets déjà rencontrées (avec leur liste de paramètres), et à droite les méthodes associées à ces classes (également avec leurs paramètres). Laissez de la place pour compléter ultérieurement.

Exemple graphique : deux dessins alternés

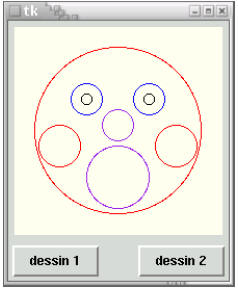
Cet autre exemple vous montrera comment vous pouvez exploiter les connaissances que vous avez acquises précédemment, concernant les boucles, les listes et les fonctions, afin de réaliser de nombreux dessins avec seulement quelques lignes de code. Il s’agit d’une petite application qui affiche l’un ou l’autre des deux dessins reproduits ci-dessous, en fonction du bouton choisi :

from tkinter import *

def cercle(x, y, r, coul ='black'):
    "tracé d'un cercle de centre (x,y) et de rayon r"
    can.create_oval(x-r, y-r, x+r, y+r, outline=coul)

def figure_1():
    "dessiner une cible"
    # Effacer d'abord tout dessin préexistant :
    can.delete(ALL)
    # tracer les deux lignes (vert. Et horiz.) :
    can.create_line(100, 0, 100, 200, fill ='blue')
    can.create_line(0, 100, 200, 100, fill ='blue')
    # tracer plusieurs cercles concentriques :
    rayon = 15
    while rayon < 100:
    cercle(100, 100, rayon)
    rayon += 15

def figure_2():
    "dessiner un visage simplifié"
    # Effacer d'abord tout dessin préexistant :
    can.delete(ALL)
    # Les caractéristiques de chaque cercle sont
    # placées dans une liste de listes :
    cc =[[100, 100, 80, 'red'], # visage
        [70, 70, 15, 'blue'], # yeux
        [130, 70, 15, 'blue'],
        [70, 70, 5, 'black'],
        [130, 70, 5, 'black'],
        [44, 115, 20, 'red'], # joues
    [156, 115, 20, 'red'],
    [100, 95, 15, 'purple'], # nez
    [100, 145, 30, 'purple']] # bouche

# on trace tous les cercles à l'aide d'une boucle :
i =0
while i < len(cc): # parcours de la liste
    el = cc[i] # chaque élément est lui-même une liste
    cercle(el[0], el[1], el[2], el[3])
    i += 1

##### Programme principal : ############

fen = Tk()
can = Canvas(fen, width =200, height =200, bg ='ivory')
can.pack(side =TOP, padx =5, pady =5)
b1 = Button(fen, text ='dessin 1', command =figure_1)
b1.pack(side =LEFT, padx =3, pady =3)
b2 = Button(fen, text ='dessin 2', command =figure_2)
b2.pack(side =RIGHT, padx =3, pady =3)
fen.mainloop()

Commençons par analyser le programme principal, à la fin du script : Nous y créons une fenêtre, par instanciation d’un objet de la classe Tk() dans la variable fen.

Ensuite, nous installons 3 widgets dans cette fenêtre : un canevas et deux boutons. Le canevas est instancié dans la variable can, et les deux boutons dans les variables b1 et b2.

Comme dans le script précédent, les widgets sont mis en place dans la fenêtre à l’aide de leur méthode pack(), mais cette fois nous utilisons celle-ci avec des options :

• l’option side peut accepter les valeurs TOP, BOTTOM, LEFT ou RIGHT, pour « pousser » le widget du côté correspondant dans la fenêtre. Ces noms écrits en majuscules sont en fait ceux d’une série de variables importées avec le module tkinter, et que vous pouvez considérer comme des « pseu- do-constantes ».

• les options padx et pady permettent de réserver un petit espace autour du widget. Cet espace est exprimé en nombre de pixels : padx réserve un espace à gauche et à droite du widget, pady réserve un espace au-dessus et au-dessous du widget.

Les boutons commandent l’affichage des deux dessins, en invoquant les fonctions figure_1() et fi- gure_2(). Considérant que nous aurions à tracer un certain nombre de cercles dans ces dessins, nous avons estimé qu’il serait bien utile de définir d’abord une fonction cercle() spécialisée.

En effet, vous savez probablement déjà que le canevas tkinter est doté d’une méthode create_oval() qui permet de dessiner des ellipses quelconques (et donc aussi des cercles), mais cette méthode doit être invoquée avec quatre arguments qui seront les coordonnées des coins supérieur gauche et inférieur droit d’un rectangle fictif, dans lequel l’ellipse viendra alors s’inscrire.

Cela n’est pas très pratique dans le cas particulier du cercle : il nous semblera plus naturel de commander ce tracé en fournissant les coordonnées de son centre ainsi que son rayon. C’est ce que nous obtiendrons avec notre fonction cercle(), laquelle invoque la méthode create_oval() en effectuant la conversion des coordonnées.

Remarquez aussi que cette fonction attend un argument facultatif en ce qui concerne la couleur du cercle à tracer (noir par défaut). L’efficacité de cette approche apparaît clairement dans la fonction figure_1(), ou nous trouvons une simple boucle de répétition pour dessiner toute la série de cercles (de même centre et de rayon croissant).

Notez au passage l’utilisation de l’opérateur += qui permet d’incrémenter une variable (dans notre exemple, la variable r voit sa valeur augmenter de 15 unités à chaque itération). Le second dessin est un peu plus complexe, parce qu’il est composé de cercles de tailles variées centrés sur des points différents.

Nous pouvons tout de même tracer tous ces cercles à l’aide d’une seule boucle de répétition, si nous mettons à profit nos connaissances concernant les listes. En effet, ce qui différencie les cercles que nous voulons tracer tient en quatre caractéristiques : coordonnées x et y du centre, rayon et couleur.

Pour chaque cercle, nous pouvons placer ces quatre caractéristiques dans une petite liste, et rassembler toutes les petites listes ainsi obtenues dans une autre liste plus grande. Nous disposerons ainsi d’une liste de listes, qu’il suffira ensuite de parcourir à l’aide d’une boucle pour effectuer les tracés correspondants.

Exercices

8.9 Inspirez-vous du script précédent pour écrire une petite application qui fait apparaître un damier (dessin de cases noires sur fond blanc) lorsque l’on clique sur un bouton :

8.10 À l’application de l’exercice précédent, ajoutez un bouton qui fera apparaître des pions au hasard sur le damier (chaque pression sur le bouton fera apparaître un nouveau pion).

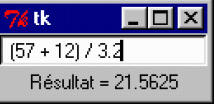
Exemple graphique : calculatrice minimaliste

Bien que très court, le petit script ci-dessous implémente une calculatrice complète, avec laquelle vous pourrez même effectuer des calculs comportant des parenthèses et des fonctions scientifiques. N’y voyez rien d’extraordinaire. Toute cette fonctionnalité n’est qu’une conséquence du fait que vous utilisez un interpréteur plutôt qu’un compilateur pour exécuter vos programmes.

Comme vous le savez, le compilateur n’intervient qu’une seule fois, pour traduire l’ensemble de votre code source en un programme exécutable. Son rôle est donc terminé avant même l’exécution du programme.

L’interpréteur, quant à lui, est toujours actif pendant l’exécution du programme, et donc tout à fait disponible pour traduire un nouveau code source quelconque, comme une expression mathématique entrée au clavier par l’utilisateur. Les langages interprétés disposent donc toujours de fonctions permettant d’évaluer une chaîne de caractères comme une suite d’instructions du langage lui-même.

Il devient alors possible de construire en peu de lignes des structures de programmes très dynamiques. Dans l’exemple ci-dessous, nous utilisons la fonction intégrée eval() pour analyser l’expression mathématique entrée par l’utilisateur dans le champ prévu à cet effet, et nous n’avons plus ensuite qu’à afficher le résultat.

# Exercice utilisant la bibliothèque graphique tkinter et le module math
from tkinter import *
from math import *

# définition de l'action à effectuer si l'utilisateur actionne
# la touche "enter" alors qu'il édite le champ d'entrée :

def evaluer(event):
    chaine.configure(text = "Résultat = " + str(eval(entree.get())))

# ----- Programme principal : -----
fenetre = Tk()
entree = Entry(fenetre)
entree.bind("<Return>", evaluer)
chaine = Label(fenetre)
entree.pack()
chaine.pack()
fenetre.mainloop()

Au début du script, nous commençons par importer les modules tkinter et math, ce dernier étant nécessaire afin que la dite calculatrice puisse disposer de toutes les fonctions mathématiques et scientifiques usuelles : sinus, cosinus, racine carrée, etc.

Ensuite nous définissons une fonction evaluer(), qui sera en fait la commande exécutée par le programme lorsque l’utilisateur actionnera la touche Return (ou Enter) après avoir entré une expression mathématique quelconque dans le champ d’entrée décrit plus loin. Cette fonction utilise la méthode configure() du widget chaine, pour modifier son attribut text.

L’attribut en question reçoit donc ici une nouvelle valeur, déterminée par ce que nous avons écrit à la droite du signe égale : il s’agit en l’occurrence d’une chaîne de caractères construite dynamiquement, à l’aide de deux fonctions intégrées dans Python :

eval() et str(),

et d’une méthode associée à un widget tkinter : la méthode get(). eval() fait appel à l’interpréteur pour évaluer une expression Python qui lui est transmise dans une chaîne de caractères.

Le résultat de l’évaluation est fourni en retour.

Exemple :

chaine = "(25 + 8)/3" # chaîne contenant une expression mathématique
res = eval(chaine) # évaluation de l'expression contenue dans la chaîne
print(res +5) # => le contenu de la variable res est numérique

str() transforme une expression numérique en chaîne de caractères. Nous devons faire appel à cette fonction parce que la précédente renvoie une valeur numérique, que nous convertissons à nouveau en chaîne de caractères pour pouvoir l’incorporer au message Résultat =.

get() est une méthode associée aux widgets de la classe Entry. Dans notre petit programme exemple, nous utilisons un widget de ce type pour permettre à l’utilisateur d’entrer une expression numérique quelconque à l’aide de son clavier. La méthode get() permet en quelque sorte « d’extraire » du widget entree la chaîne de caractères qui lui a été fournie par l’utilisateur.

Le corps du programme principal contient la phase d’initialisation, qui se termine par la mise en route de l’observateur d’évènements (mainloop). On y trouve l’instanciation d’une fenêtre Tk(), contenant un widget chaine instancié à partir de la classe Label(), et un widget entree instancié à partir de la classe Entry().

Attention : afin que ce dernier widget puisse vraiment faire son travail, c’est-à-dire transmettre au programme l’expression que l’utilisateur y aura encodée, nous lui associons un évènement à l’aide de la méthode bind():

entree.bind("<Return>",evaluer)

Cette instruction signifie : « Lier l’évènement <pression sur la touche Return> à l’objet <entree>, le gestionnaire de cet évènement étant la fonction <evaluer> ».

L’évènement à prendre en charge est décrit dans une chaîne de caractères spécifique (dans notre exemple, il s’agit de la chaîne "<Return>". Il existe un grand nombre de ces évènements (mouvements et clics de la souris, enfoncement des touches du clavier, positionnement et redimensionnement des fenêtres, passage au premier plan, etc.).

Vous trouverez la liste des chaînes spécifiques de tous ces évènements dans les ouvrages de référence traitant de tkinter.

Remarquez bien qu’il n’y a pas de parenthèses après le nom de la fonction evaluer. En effet : dans cette instruction, nous ne souhaitons pas déjà invoquer la fonction elle-même (ce serait prématuré) ; ce que nous voulons, c’est établir un lien entre un type d’évènement particulier et cette fonction, de manière à ce qu’elle soit invoquée plus tard, chaque fois que l’évènement se produira.

Si nous mettions des parenthèses, l’argument qui serait transmis à la méthode bind() serait la valeur de retour de cette fonction et non sa référence. Profitons aussi de l’occasion pour observer encore une fois la syntaxe des instructions destinées à mettre en œuvre une méthode associée à un objet :

objet.méthode(arguments)

On écrit d’abord le nom de l’objet sur lequel on désire intervenir, puis le point (qui fait office d’opéra- teur), puis le nom de la méthode à mettre en œuvre ; entre les parenthèses associées à cette méthode, on indique enfin les arguments qu’on souhaite lui transmettre.

Exemple graphique : détection et positionnement d’un clic de souris

Dans la définition de la fonction « evaluer » de l’exemple précédent, vous aurez remarqué que nous avons fourni un argument event (entre les parenthèses). Cet argument est obligatoire.

Lorsque vous définissez une fonction gestionnaire d’évènement qui est associée à un widget quelconque à l’aide de sa méthode bind(), vous devez toujours l’utiliser comme premier argument.

Cet argument désigne en effet un objet créé automatiquement par tkinter, qui permet de transmettre au gestionnaire d’évènement un certain nombre d’attributs de l’évènement :

• le type d’évènement : déplacement de la souris, enfoncement ou relâchement de l’un de ses boutons, appui sur une touche du clavier, entrée du curseur dans une zone prédéfinie, ouverture ou fermeture d’une fenêtre, etc.

• une série de propriétés de l’évènement : l’instant où il s’est produit, ses coordonnées, les caractéristiques du ou des widget(s) concerné(s), etc. Nous n’allons pas entrer dans trop de détails. Si vous voulez bien encoder et expérimenter le petit script ci-dessous, vous aurez vite compris le principe.

# Détection et positionnement d'un clic de souris dans une fenêtre :
from tkinter import *

def pointeur(event):
    chaine.configure(text = "Clic détecté en X =" + str(event.x) +\
    ", Y =" + str(event.y))
fen = Tk()
cadre = Frame(fen, width =200, height =150, bg="light yellow")
cadre.bind("<Button-1>", pointeur)
cadre.pack()
chaine = Label(fen)
chaine.pack()
fen.mainloop()

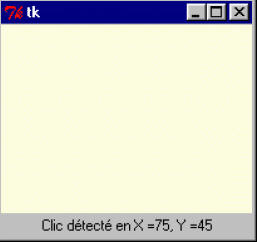
Le script fait apparaître une fenêtre contenant un cadre (Frame) rectangulaire de couleur jaune pâle, dans lequel l’utilisateur est invité à effectuer des clics de souris.

La méthode bind() du widget cadre associe l’évènement <clic à l’aide du premier bouton de la souris> au gestionnaire d’évènement « pointeur ».

Ce gestionnaire d’évènement peut utiliser les attributs x et y de l’objet event généré automatiquement par tkinter, pour construire la chaîne de caractères qui affichera la position de la souris au moment du clic.

Exercice

8.11 Modifiez le script ci-dessus de manière à faire apparaître un petit cercle rouge à l’endroit où l’utilisateur a effectué son clic (vous devrez d’abord remplacer le widget Frame par un widget Canvas).

Les classes de widgets tkinter

Note Tout au long de cet ouvrage, nous vous présenterons petit à petit le mode d’utilisation d’un certain nombre de widgets. Comprenez bien cependant qu’il n’entre pas dans nos intentions de fournir ici un manuel de référence complet sur tkinter. Nous limiterons nos explications aux widgets qui nous semblent les plus intéressants d’un point de vue didactique, c’est-à-dire ceux qui pourront nous aider à mettre en évidence des concepts de programmation importants, tels ceux de classe et d’objet. Veuillez donc consulter la littérature si vous souhaitez davantage de précisions.

Il existe 15 classes de base pour les widgets tkinter :

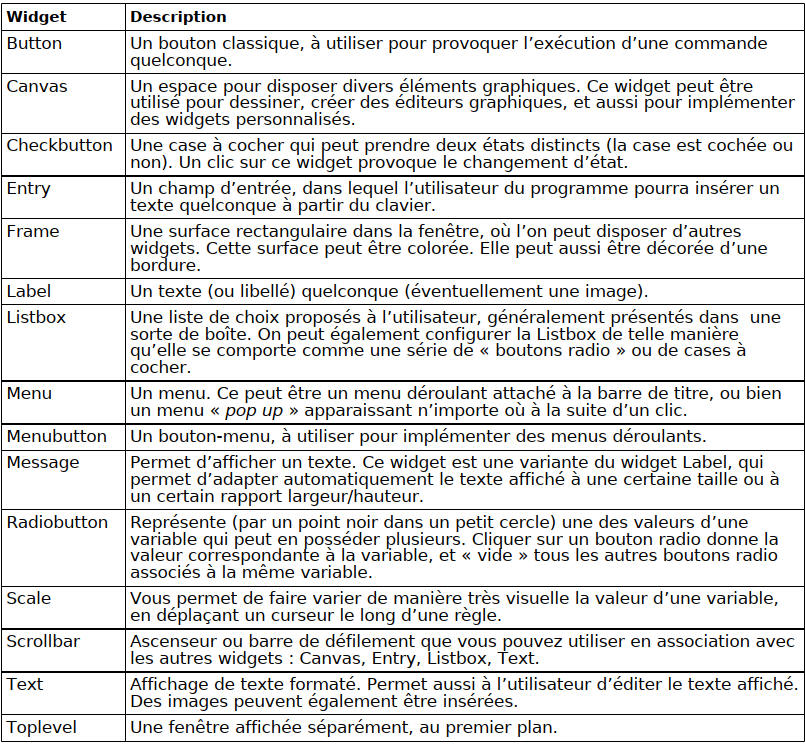
Ces classes de widgets intègrent chacune un grand nombre de méthodes. On peut aussi leur associer (lier) des évènements, comme nous venons de le voir dans les pages précédentes.

Vous allez apprendre en outre que tous ces widgets peuvent être positionnés dans les fenêtres à l’aide de trois méthodes différentes : la méthode grid(), la méthode pack() et la méthode place().

L’utilité de ces méthodes apparaît clairement lorsque l’on s’efforce de réaliser des programmes portables (c’est-à-dire susceptibles de fonctionner de manière identique sur des systèmes d’exploitation aussi différents que Unix, Mac OS ou Windows), et dont les fenêtres soient redimensionnables.

Utilisation de la méthode grid pour contrôler la disposition des widgets

Jusqu’à présent, nous avons toujours disposé les widgets dans leur fenêtre à l’aide de la méthode pack(). Cette méthode présentait l’avantage d’être extraordinairement simple, mais elle ne nous donnait pas beaucoup de liberté pour disposer les widgets à notre guise.

Comment faire, par exemple, pour obtenir la fenêtre ci-contre ? Nous pourrions effectuer un certain nombre de tentatives en fournissant à la méthode pack() des arguments de type « side = », comme nous l’avons déjà fait précédemment, mais cela ne nous mène pas très loin.

Essayons par exemple :

from tkinter import *

fen1 = Tk()
txt1 = Label(fen1, text = 'Premier champ :')
txt2 = Label(fen1, text = 'Second :')
entr1 = Entry(fen1)
entr2 = Entry(fen1)
txt1.pack(side =LEFT)
txt2.pack(side =LEFT)
entr1.pack(side =RIGHT)
entr2.pack(side =RIGHT)
fen1.mainloop()

... mais le résultat n’est pas vraiment celui que nous recherchions !

Pour mieux comprendre comment fonctionne la méthode pack(), vous pouvez encore essayer différentes combinaisons d’options, telles que side =TOP, side =BOTTOM, pour chacun de ces quatre widgets. Mais vous n’arriverez certainement pas à obtenir ce qui vous a été demandé.

Vous pourriez peut-être y parvenir en définissant deux widgets Frame() supplémentaires, et en y incorporant ensuite séparément les widgets Label() et Entry(). Cela devient fort compliqué.

Il est temps que nous apprenions à utiliser une autre approche du problème. Veuillez donc analyser le script ci-dessous : il contient en effet (presque) la solution :

from tkinter import *

fen1 = Tk()
txt1 = Label(fen1, text = 'Premier champ :')
txt2 = Label(fen1, text = 'Second :')
entr1 = Entry(fen1)
entr2 = Entry(fen1)
txt1.grid(row =0)
txt2.grid(row =1)
entr1.grid(row =0, column =1)
entr2.grid(row =1, column =1)
fen1.mainloop()

Dans ce script, nous avons donc remplacé la méthode pack() par la méthode grid(). Comme vous pouvez le constater, l’utilisation de la méthode grid() est très simple. Cette méthode considère la fenêtre comme un tableau (ou une grille). Il suffit alors de lui indiquer dans quelle ligne (row) et dans quelle colonne (column) de ce tableau on souhaite placer les widgets.

On peut numéroter les lignes et les colonnes comme on veut, en partant de zéro, ou de un, ou encore d’un nombre quelconque : tkinter ignorera les lignes et colonnes vides. Notez cependant que si vous ne fournissez aucun numéro pour une ligne ou une colonne, la valeur par défaut sera zéro. Tkinter détermine automatiquement le nombre de lignes et de colonnes nécessaire.

Mais ce n’est pas tout : si vous examinez en détail la petite fenêtre produite par le script ci-dessus, vous constaterez que nous n’avons pas encore tout à fait atteint le but poursuivi. Les deux chaînes apparaissant dans la partie gauche de la fenêtre sont centrées, alors que nous souhaitions les aligner l’une et l’autre par la droite. Pour obtenir ce résultat, il nous suffit d’ajouter un argument dans l’appel de la méthode grid() utilisée pour ces widgets.

L’option sticky peut prendre l’une des quatre valeurs N, S, W, E (les quatre points cardinaux en anglais). En fonction de cette valeur, on obtiendra un alignement des widgets par le haut, par le bas, par la gauche ou par la droite. Remplacez donc les deux premières instructions grid() du script par :

txt1.grid(row =0, sticky =E)
txt2.grid(row =1, sticky =E)

... et vous atteindrez enfin exactement le but recherché. Analysons à présent la fenêtre suivante :

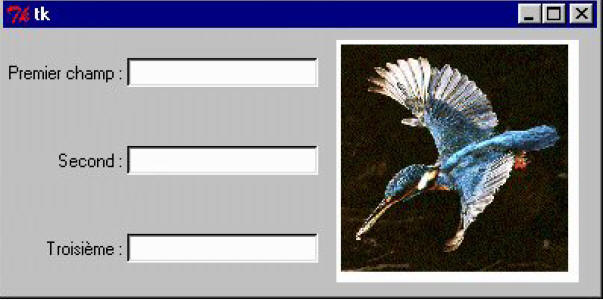
Cette fenêtre comporte 3 colonnes : une première avec les 3 chaînes de caractères, une seconde avec les 3 champs d’entrée, et une troisième avec l’image. Les deux premières colonnes comportent chacune 3 lignes, mais l’image située dans la dernière colonne s’étale en quelque sorte sur les trois.

Le code correspondant est le suivant :

from tkinter import *

fen1 = Tk()

# création de widgets 'Label' et 'Entry' :
txt1 = Label(fen1, text ='Premier champ :')
txt2 = Label(fen1, text ='Second :')
txt3 = Label(fen1, text ='Troisième :')
entr1 = Entry(fen1)
entr2 = Entry(fen1)
entr3 = Entry(fen1)

# création d'un widget 'Canvas' contenant une image bitmap :
can1 = Canvas(fen1, width =160, height =160, bg ='white')
photo = PhotoImage(file ='martin_p.gif')
item = can1.create_image(80, 80, image =photo)

# Mise en page à l'aide de la méthode 'grid' :
txt1.grid(row =1, sticky =E)
txt2.grid(row =2, sticky =E)
txt3.grid(row =3, sticky =E)
entr1.grid(row =1, column =2)
entr2.grid(row =2, column =2)
entr3.grid(row =3, column =2)
can1.grid(row =1, column =3, rowspan =3, padx =10, pady =5)

# démarrage :
fen1.mainloop()

Pour pouvoir faire fonctionner ce script, il vous faudra probablement remplacer le nom du fichier image (martin_p.gif) par le nom d’une image de votre choix.

Attention : la bibliothèque tkinter standard n’accepte qu’un petit nombre de formats pour cette image. Choisissez de préférence le format GIF. Nous pouvons remarquer un certain nombre de choses dans ce script :

1. La technique utilisée pour incorporer une image : tkinter ne permet pas d’insérer directement une image dans une fenêtre. Il faut d’abord installer un canevas, et ensuite positionner l’image dans celui-ci. Nous avons opté pour un canevas de couleur blanche, afin de pouvoir le distinguer de la fenêtre. Vous pouvez remplacer le paramètre bg ='white' par bg ='gray' si vous souhaitez que le canevas devienne invisible. Étant donné qu’il existe de nombreux types d’images, nous devons en outre déclarer l’objet image comme étant un bitmap GIF, à partir de la classe PhotoImage().

2. La ligne où nous installons l’image dans le canevas est la ligne : item = can1.create_image(80, 80, image =photo) Pour employer un vocabulaire correct, nous dirons que nous utilisons ici la méthode create_image() associée à l’objet can1 (lequel objet est lui-même une instance de la classe Canvas). Les deux premiers arguments transmis (80, 80) indiquent les coordonnées x et y du canevas où il faut placer le centre de l’image. Les dimensions du canevas étant de 160x160, notre choix aboutira donc à un centrage de l’image au milieu du canevas.

3. La numérotation des lignes et colonnes dans la méthode grid() : On peut constater que la numérotation des lignes et des colonnes dans la méthode grid() utilisée ici commence cette fois à partir de 1 (et non à partir de zéro comme dans le script précédent). Comme nous l’avons déjà signalé plus haut, ce choix de numérotation est tout à fait libre. On pourrait tout aussi bien numéroter : 5, 10, 15, 20... puisque tkinter ignore les lignes et les colonnes vides. Numéroter à partir de l augmente probablement la lisibilité de notre code.

4. Les arguments utilisés avec grid() pour positionner le canevas : can1.grid(row =1, column =3, rowspan =3, padx =10, pady =5) Les deux premiers arguments indiquent que le canevas sera placé dans la première ligne de la troisième colonne. Le troisième (rowspan =3) indique qu’il pourra « s’étaler » sur trois lignes. Les deux derniers (padx =10, pady =5) indiquent la dimension de l’espace qu’il faut réserver autour de ce widget (en largeur et en hauteur).

5. Et tant que nous y sommes, profitons de cet exemple de script, que nous avons déjà bien décortiqué, pour apprendre à simplifier quelque peu notre code…

Composition d’instructions pour écrire un code plus compact

Python étant un langage de programmation de haut niveau, il est souvent possible (et souhaitable) de retravailler un script afin de le rendre plus compact.

Vous pouvez par exemple assez fréquemment utiliser la composition d’instructions pour appliquer la méthode de mise en page des widgets (grid(), pack() ou place()) au moment même où vous créez ces widgets. Le code correspondant devient alors un peu plus simple, et parfois plus lisible. Vous pouvez par exemple remplacer les deux lignes :

txt1 = Label(fen1, text ='Premier champ :')
txt1.grid(row =1, sticky =E)

du script précédent par une seule, telle que :

Label(fen1, text ='Premier champ :').grid(row =1, sticky =E)

Dans cette nouvelle écriture, vous pouvez constater que nous faisons l’économie de la variable intermédiaire txt1. Nous avions utilisé cette variable pour bien dégager les étapes successives de notre démarche, mais elle n’est pas toujours indispensable.

Le simple fait d’invoquer la classe Label() provoque en effet l’instanciation d’un objet de cette classe, même si l’on ne mémorise pas la référence de cet objet dans une variable (tkinter la conserve de toute façon dans sa représentation interne de la fenêtre).

Si l’on procède ainsi, la référence est perdue pour le restant du script, mais elle peut tout de même être transmise à une méthode de mise en page telle que grid() au moment même de l’instancia- tion, en une seule instruction composée. Voyons cela un peu plus en détail.

Jusqu’à présent, nous avons créé des objets divers (par instanciation à partir d’une classe quelconque), en les affectant à chaque fois à des variables.

Par exemple, lorsque nous avons écrit :

txt1 = Label(fen1, text ='Premier champ :')

nous avons créé une instance de la classe Label(), que nous avons assignée à la variable txt1.

La variable txt1 peut alors être utilisée pour faire référence à cette instance, partout ailleurs dans le script, mais dans les faits nous ne l’utilisons qu’une seule fois pour lui appliquer la méthode grid(), le widget dont il est question n’étant rien d’autre qu’une simple étiquette descriptive.

Or, créer ainsi une nouvelle variable pour n’y faire référence ensuite qu’une seule fois (et directement après sa création) n’est pas une pratique très recommandable, puisqu’elle consiste à réserver inutilement un certain espace mémoire. Lorsque ce genre de situation se présente, il est plus judicieux d’utiliser la composition d’instructions.

Par exemple, on préfèrera le plus souvent remplacer les deux instructions :

somme = 45 + 72
print (somme)

par une seule instruction composée, telle que :

print (45 + 72)
on fait ainsi l’économie d’une variable.

De la même manière, lorsque l’on met en place des widgets auxquels on ne souhaite plus revenir par la suite, comme c’est souvent le cas pour les widgets de la classe Label(), on peut en général appliquer la méthode de mise en page (grid() , pack() ou place()) directement au moment de la création du widget, en une seule instruction composée.

Cela s’applique seulement aux widgets qui ne sont plus référencés après qu’on les ait créés. Tous les autres doivent impérativement être assignés à des variables, afin que l’on puisse encore interagir avec eux ailleurs dans le script. Et dans ce cas, il faut obligatoirement utiliser deux instructions distinctes, l’une pour instancier le widget, et l’autre pour lui appliquer ensuite la méthode de mise en page.

Vous ne pouvez pas, par exemple, construire une instruction composée telle que :

 entree = Entry(fen1).pack() # faute de programmation !!!

En apparence, cette instruction devrait instancier un nouveau widget et l’assigner à la variable en- tree, la mise en page s’effectuant dans la même opération à l’aide de la méthode pack().

Dans la réalité, cette instruction produit bel et bien un nouveau widget de la classe Entry(), et la méthode pack() effectue bel et bien sa mise en page dans la fenêtre, mais la valeur qui est mémorisée dans la variable entree n’est pas la référence du widget !

C’est la valeur de retour de la méthode pack() : vous devez vous rappeler en effet que les méthodes, comme les fonctions, renvoient toujours une valeur au programme qui les appelle. Et vous ne pouvez rien faire de cette valeur de retour : il s’agit en l’occurrence d’un objet vide (None).

Pour obtenir une vraie référence du widget, vous devez obligatoirement utiliser deux instructions :

entree = Entry(fen1) # instanciation du widget
entree.pack() # application de la mise en page

Lorsque vous utilisez la méthode grid(), vous pouvez simplifier encore un peu votre code, en omettant l’indication de nombreux numéros de lignes et de colonnes.

À partir du moment où c’est la la méthode grid() qui est utilisée pour positionner les widgets, tkinter considère en effet qu’il existe forcément des lignes et des colonnes.

Si un numéro de ligne ou de colonne n’est pas indiqué, le widget correspondant est placé dans la première case vide disponible.

Le script ci-dessous intègre les simplifications que nous venons d’expliquer :
from tkinter import *

fen1 = Tk()

# création de widgets Label(), Entry(), et Checkbutton() :
Label(fen1, text = 'Premier champ :').grid(sticky =E)
Label(fen1, text = 'Deuxième :').grid(sticky =E)
Label(fen1, text = 'Troisième :').grid(sticky =E)
entr1 = Entry(fen1)
entr2 = Entry(fen1) # ces widgets devront certainement
entr3 = Entry(fen1) # être référencés plus loin :
entr1.grid(row =0, column =1) # il faut donc les assigner chacun
entr2.grid(row =1, column =1) # à une variable distincte
entr3.grid(row =2, column =1)
chek1 = Checkbutton(fen1, text ='Case à cocher, pour voir')
chek1.grid(columnspan =2)

# création d'un widget 'Canvas' contenant une image bitmap :
can1 = Canvas(fen1, width =160, height =160, bg ='white')
photo = PhotoImage(file ='Martin_P.gif')
can1.create_image(80,80, image =photo)
can1.grid(row =0, column =2, rowspan =4, padx =10, pady =5)

# démarrage :
fen1.mainloop()

Modification des propriétés d’un objet – Animation

À ce stade de votre apprentissage, vous souhaitez probablement pouvoir faire apparaître un petit dessin quelconque dans un canevas, et puis le déplacer à volonté, par exemple à l’aide de boutons.

Veuillez donc écrire, tester, puis analyser le script ci-dessous :

from tkinter import *

# procédure générale de déplacement :
def avance(gd, hb):
    global x1, y1
    x1, y1 = x1 +gd, y1 +hb
    can1.coords(oval1, x1,y1, x1+30,y1+30)

# gestionnaires d'événements :
def depl_gauche():
    avance(-10, 0)

def depl_droite():
    avance(10, 0)

def depl_haut():
    avance(0, -10)

def depl_bas():
avance(0, 10)

#------ Programme principal -------
# les variables suivantes seront utilisées de manière globale :
x1, y1 = 10, 10 # coordonnées initiales

# Création du widget principal ("maître") :
fen1 = Tk()
fen1.title("Exercice d'animation avec tkinter")

# création des widgets "esclaves" :
can1 = Canvas(fen1,bg='dark grey',height=300,width=300)
oval1 = can1.create_oval(x1,y1,x1+30,y1+30,width=2,fill='red')
can1.pack(side=LEFT)
Button(fen1,text='Quitter',command=fen1.quit).pack(side=BOTTOM)
Button(fen1,text='Gauche',command=depl_gauche).pack()
Button(fen1,text='Droite',command=depl_droite).pack()
Button(fen1,text='Haut',command=depl_haut).pack()
Button(fen1,text='Bas',command=depl_bas).pack()

# démarrage du réceptionnaire d’évènements (boucle principale) :
fen1.mainloop()

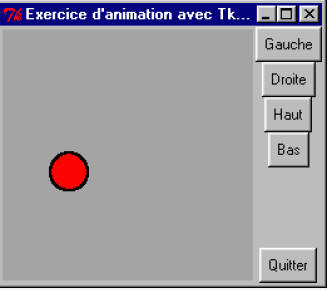
Le corps de ce programme reprend de nombreux éléments connus : nous y créons une fenêtre fen1, dans laquelle nous installons un canevas contenant lui-même un cercle coloré, plus cinq boutons de contrôle.

Veuillez remarquer au passage que nous n’instancions pas les widgets boutons dans des variables (c’est inutile, puisque nous n’y faisons plus référence par la suite) : nous devons donc appliquer la méthode pack() directement au moment de la création de ces objets. La vraie nouveauté de ce programme réside dans la fonction avance() définie au début du script.

Chaque fois qu’elle sera appelée, cette fonction redéfinira les coordonnées de l’objet « cercle coloré » que nous avons installé dans le canevas, ce qui provoquera l’animation de cet objet. Cette manière de procéder est tout à fait caractéristique de la programmation « orientée objet » : on commence par créer des objets, puis on agit sur ces objets en modifiant leurs propriétés, par l’intermédiaire de méthodes.

En programmation impérative « à l’ancienne » (c’est-à-dire sans utilisation d’objets), on anime des figures en les effaçant à un endroit pour les redessiner ensuite un petit peu plus loin. En programmation « orientée objet », par contre, ces tâches sont prises en charge automatiquement par les classes dont les objets dérivent, et il ne faut donc pas perdre son temps à les reprogrammer.

Exercices

8.12 Écrivez un programme qui fait apparaître une fenêtre avec un canevas. Dans ce canevas on verra deux cercles (de tailles et de couleurs différentes), qui sont censés représenter deux astres. Des boutons doivent permettre de les déplacer à volonté tous les deux dans toutes les directions. Sous le canevas, le programme doit afficher en permanence :

a) la distance séparant les deux astres;

b) la force gravitationnelle qu’ils exercent l’un sur l’autre (penser à afficher en haut de fenêtre les masses choisies pour chacun d’eux, ainsi que l’échelle des distances). Dans cet exercice, vous utiliserez évidemment la loi de la gravitation universelle de Newton.

8.13 En vous inspirant du programme qui détecte les clics de souris dans un canevas, modifiez le programme ci-dessus pour y réduire le nombre de boutons : pour déplacer un astre, il suffira de le choisir avec un bouton, et ensuite de cliquer sur le canevas pour que cet astre se positionne à l’endroit où l’on a cliqué.

8.14 Extension du programme ci-dessus. Faire apparaître un troisième astre, et afficher en permanence la force résultante agissant sur chacun des trois (en effet : chacun subit en permanence l’attraction gravitationnelle exercée par les deux autres !).

8.15 Même exercice avec des charges électriques (loi de Coulomb). Donner cette fois une possibilité de choisir le signe des charges.

8.16 Écrivez un petit programme qui fait apparaître une fenêtre avec deux champs : l’un indique une température en degrés Celsius, et l’autre la même température exprimée en degrés Fahrenheit. Chaque fois que l’on change une quelconque des deux températures, l’autre est corrigée en conséquence. Pour convertir les degrés Fahrenheit en Celsius et vice-versa, on utilise la formule T F =T C ×1,8032 . Revoyez aussi le petit programme concernant la calculatrice simplifiée (page 90).

8.17 Écrivez un programme qui fait apparaître une fenêtre avec un canevas. Dans ce canevas, placez un petit cercle censé représenter une balle. Sous le canevas, placez un bouton. Chaque fois que l’on clique sur le bouton, la balle doit avancer d’une petite distance vers la droite, jusqu’à ce qu’elle atteigne l’extrémité du canevas. Si l’on continue à cliquer, la balle doit alors revenir en arrière jusqu’à l’autre extrémité, et ainsi de suite.

8.18 Améliorez le programme ci-dessus pour que la balle décrive cette fois une trajectoire circulaire ou elliptique dans le canevas (lorsque l’on clique continuellement). Note : pour arriver au résultat escompté, vous devrez nécessairement définir une variable qui représentera l’angle décrit, et utiliser les fonctions sinus et cosinus pour positionner la balle en fonction de cet angle.

8.19 Modifiez le programme ci-dessus de telle manière que la balle, en se déplaçant, laisse derrière elle une trace de la trajectoire décrite.

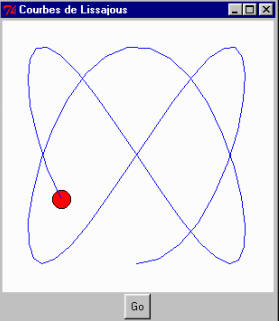
8.20 Modifiez le programme ci-dessus de manière à tracer d’autres figures. Consultez votre professeur pour des suggestions (courbes de Lissajous).

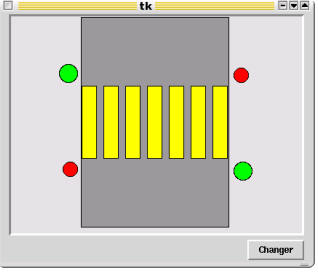
8.21 Écrivez un programme qui fait apparaître une fenêtre avec un canevas et un bouton. Dans le canevas, tracez un rectangle gris foncé, lequel représentera une route, et par-dessus, une série de rectangles jaunes censés représenter un passage pour piétons. Ajoutez quatre cercles colorés pour figurer les feux de circulation concernant les piétons et les véhicules. Chaque utilisation du bouton devra provoquer le changement de couleur des feux :

8.22 Écrivez un programme qui montre un canevas dans lequel est dessiné un circuit électrique simple (générateur + interrupteur + résistance). La fenêtre doit être pourvue de champs d’entrée qui permettront de paramétrer chaque élément (c’est-à-dire choisir les valeurs des résistances et tensions). L’interrupteur doit être fonctionnel (prévoyez un bouton <Marche/arrêt> pour cela). Des « étiquettes » doivent afficher en permanence les tensions et intensités résultant des choix effectués par l’utilisateur.

Animation automatique – Récursivité

Pour conclure cette première prise de contact avec l’interface graphique tkinter, voici un dernier exemple d’animation, qui fonctionne cette fois de manière autonome dès qu’on l’a mise en marche.

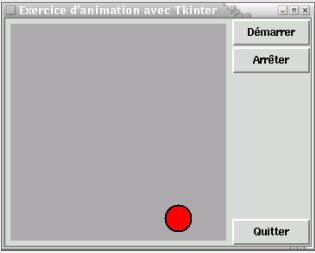
from tkinter import *

# définition des gestionnaires
# d'événements :

def move():
    "déplacement de la balle"
    global x1, y1, dx, dy, flag
    x1, y1 = x1 +dx, y1 + dy
    if x1 >210:
        x1, dx, dy = 210, 0, 15
    if y1 >210:
        y1, dx, dy = 210, -15, 0
    if x1 <10:
        x1, dx, dy = 10, 0, -15
    if y1 <10:
        y1, dx, dy = 10, 15, 0
    can1.coords(oval1,x1,y1,x1+30,y1+30)
    if flag >0:
        fen1.after(50,move) # => boucler, après 50 millisecondes

def stop_it():
    "arrêt de l'animation"
    global flag
    flag =0

def start_it():
"démarrage de l'animation"
global flag
if flag ==0: # pour ne lancer qu’une seule boucle
    flag =1
    move()

#========== Programme principal =============

# les variables suivantes seront utilisées de manière globale :
x1, y1 = 10, 10 # coordonnées initiales
dx, dy = 15, 0 # 'pas' du déplacement
flag =0 # commutateur

# Création du widget principal ("parent") :
fen1 = Tk()
fen1.title("Exercice d'animation avec tkinter")

# création des widgets "enfants" :
can1 = Canvas(fen1,bg='dark grey',height=250, width=250)
can1.pack(side=LEFT, padx =5, pady =5)
oval1 = can1.create_oval(x1, y1, x1+30, y1+30, width=2, fill='red')
bou1 = Button(fen1,text='Quitter', width =8, command=fen1.quit)
bou1.pack(side=BOTTOM)
bou2 = Button(fen1, text='Démarrer', width =8, command=start_it)
bou2.pack()
bou3 = Button(fen1, text='Arrêter', width =8, command=stop_it)
bou3.pack()

# démarrage du réceptionnaire d'événements (boucle principale) :
fen1.mainloop()

La seule nouveauté mise en œuvre dans ce script se trouve tout à la fin de la définition de la fonction move() : vous y noterez l’utilisation de la méthode after().

Cette méthode peut s’appliquer à un widget quelconque. Elle déclenche l’appel d’une fonction après qu’un certain laps de temps se soit écoulé.

Ainsi par exemple, window.after(200,qqc) déclenche pour le widget window un appel de la fonction qqc() après une pause de 200 millisecondes. Dans notre script, la fonction qui est appelée par la méthode after() est la fonction move() elle-même. Nous utilisons donc ici pour la première fois une technique de programmation très puissante, que l’on appelle récursivité.

Pour faire simple, nous dirons que la récursivité est ce qui se passe lorsqu’une fonction s’appelle elle-même. On obtient bien évidemment ainsi un bouclage, qui peut se perpétuer indéfiniment si l’on ne prévoit pas aussi un moyen pour l’interrompre.

Voyons comment cela fonctionne dans notre exemple. La fonction move() est invoquée une première fois lorsque l’on clique sur le bouton <Démarrer>.

Elle effectue son travail (c’est-à-dire positionner la balle). Ensuite, par l’intermédiaire de la méthode after(), elle s’invoque elle-même après une petite pause. Elle repart donc pour un second tour, puis s’invoque elle-même à nouveau, et ainsi de suite indéfiniment...

C’est du moins ce qui se passerait si nous n’avions pas pris la précaution de placer quelque part dans la boucle une instruction de sortie. En l’occurrence, il s’agit d’un simple test conditionnel : à chaque itération de la boucle, nous examinons le contenu de la variable flag à l’aide d’une instruction if.

Si le contenu de la variable flag est zéro, alors le bouclage ne s’effectue plus et l’animation s’arrête. Remarquez que nous avons pris la précaution de définir flag comme une variable globale.

Ainsi nous pouvons aisément changer sa valeur à l’aide d’autres fonctions, en l’occurrence celles que nous avons associées aux boutons <Démarrer> et <Arrêter>.

Nous obtenons ainsi un mécanisme simple pour lancer ou arrêter notre animation : un premier clic sur le bouton <Démarrer> assigne une valeur non-nulle à la variable flag, puis provoque immédiatement un premier appel de la fonction move().

Celle-ci s’exécute, puis continue ensuite à s’appeler elle-même toutes les 50 millisecondes, tant que flag ne revient pas à zéro. Si l’on continue à cliquer sur le bouton <Démarrer>, la fonction move() ne peut plus être appelée, parce que la valeur de flag vaut désormais 1.

On évite ainsi le démarrage de plusieurs boucles concurrentes. Le bouton <Arrêter> remet flag à zéro, et la boucle s’interrompt.

Exercices

8.23 Dans la fonction start_it(), supprimez l’instruction if flag == 0: (et l’indentation des deux lignes suivantes). Que se passe-t-il ? (Cliquez plusieurs fois sur le bouton <Démarrer>.) Tâchez d’exprimer le plus clairement possible votre explication des faits observés.

8.24 Modifiez le programme de telle façon que la balle change de couleur à chaque « virage ».

8.25 Modifiez le programme de telle façon que la balle effectue des mouvements obliques comme une bille de billard qui rebondit sur les bandes (« en zig-zag »).

8.26 Modifiez le programme de manière à obtenir d’autres mouvements. Tâchez par exemple d’obtenir un mouvement circulaire (comme dans les exercices de la page 102).

8.27 Modifiez ce programme, ou bien écrivez-en un autre similaire, de manière à simuler le mouvement d’une balle qui tombe (sous l’effet de la pesanteur), et rebondit sur le sol. Attention : il s’agit cette fois de mouvements accélérés !

8.28 À partir des scripts précédents, vous pouvez à présent écrire un programme de jeu fonctionnant de la manière suivante : une balle se déplace au hasard sur un canevas, à vitesse faible. Le joueur doit essayer de cliquer sur cette balle à l’aide de la souris. S’il y arrive, il gagne un point, mais la balle se déplace désormais un peu plus vite, et ainsi de suite. Arrêter le jeu après un certain nombre de clics et afficher le score atteint.

8.29 Variante du jeu précédent : chaque fois que le joueur parvient à « l’attraper », la balle devient plus petite (elle peut également changer de couleur).

8.30 Écrivez un programme dans lequel évoluent plusieurs balles de couleurs différentes, qui rebondissent les unes sur les autres ainsi que sur les parois.

8.31 Perfectionnez le jeu des précédents exercices en y intégrant l’algorithme ci-dessus. Il s’agit à présent pour le joueur de cliquer seulement sur la balle rouge. Un clic erroné (sur une balle d’une autre couleur) lui fait perdre des points.

8.32 Écrivez un programme qui simule le mouvement de deux planètes tournant autour du soleil sur des orbites circulaires différentes (ou deux électrons tournant autour d’un noyau d’atome...).

8.33 Écrivez un programme pour le jeu du serpent : un « serpent » (constitué en fait d’une courte ligne de carrés) se déplace sur le canevas dans l’une des 4 directions : droite, gauche, haut, bas. Le joueur peut à tout moment changer la direction suivie par le serpent à l’aide des touches fléchées du clavier. Sur le canevas se trouvent également des « proies » (des petits cercles fixes disposés au hasard). Il faut diriger le serpent de manière à ce qu’il « mange » les proies sans arriver en contact avec les bords du canevas. À chaque fois qu’une proie est mangée, le serpent s’allonge d’un carré, le joueur gagne un point, et une nouvelle proie apparaît ailleurs. La partie s’arrête lorsque le serpent touche l’une des parois, ou lorsqu’il a atteint une certaine taille.

8.34 Perfectionnement du jeu précédent : la partie s’arrête également si le serpent « se recoupe ».

Solutions des exercices

Exercice 8.7 :

from tkinter import *

# Coordonnées X,Y des 5 anneaux :
coord = [[20,30], [120,30], [220, 30], [70,80], [170,80]]

# Couleurs des 5 anneaux :
coul = ["red", "yellow", "blue", "green", "black"]
base = Tk()
can = Canvas(base, width =335, height =200, bg ="white")
can.pack()
bou = Button(base, text ="Quitter", command =base.quit)
bou.pack(side = RIGHT)

# Dessin des 5 anneaux :
i = 0
while i < 5:
    x1, y1 = coord[i][0], coord[i][1]
    can.create_oval(x1, y1, x1+100, y1 +100, width =2, outline =coul[i])
    i = i +1
base.mainloop()

Variante :

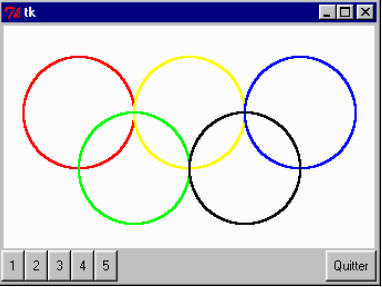
from tkinter import *

# Dessin des 5 anneaux :
def dessineCercle(i):
x1, y1 = coord[i][0], coord[i][1]
can.create_oval(x1, y1, x1+100, y1 +100, width =2, outline =coul[i])

def a1():
    dessineCercle(0)
def a2():
    dessineCercle(1)
def a3():
    dessineCercle(2)
def a4():
    dessineCercle(3)
def a5():
    dessineCercle(4)

# Coordonnées X,Y des 5 anneaux :
coord = [[20,30], [120,30], [220, 30], [70,80], [170,80]]

# Couleurs des 5 anneaux :
coul = ["red", "yellow", "blue", "green", "black"]

base = Tk()
can = Canvas(base, width =335, height =200, bg ="white")
can.pack()
bou = Button(base, text ="Quitter", command =base.quit)
bou.pack(side = RIGHT)

# Installation des 5 boutons :
Button(base, text='1', command = a1).pack(side =LEFT)
Button(base, text='2', command = a2).pack(side =LEFT)
Button(base, text='3', command = a3).pack(side =LEFT)
Button(base, text='4', command = a4).pack(side =LEFT)
Button(base, text='5', command = a5).pack(side =LEFT)
base.mainloop()

Exercices 8.9 et 8.10 :

# Dessin d'un damier, avec placement de pions au hasard

from tkinter import *
from random import randrange # générateur de nombres aléatoires

def damier():
    "dessiner dix lignes de carrés avec décalage alterné"
    y = 0
    while y < 10:
        if y % 2 == 0: # une fois sur deux, on
            x = 0 # commencera la ligne de
        else: # carrés avec un décalage
            x = 1 # de la taille d'un carré
        ligne_de_carres(x*c, y*c)
        y += 1

def ligne_de_carres(x, y):
    "dessiner une ligne de carrés, en partant de x, y"
    i = 0
    while i < 5:
        can.create_rectangle(x, y, x+c, y+c, fill='navy')
        i += 1
        x += c*2 # espacer les carrés

def cercle(x, y, r, coul):
    "dessiner un cercle de centre x,y et de rayon r"
    can.create_oval(x-r, y-r, x+r, y+r, fill=coul)

def ajouter_pion():
    "dessiner un pion au hasard sur le damier"
    # tirer au hasard les coordonnées du pion :
    x = c/2 + randrange(10) * c
    y = c/2 + randrange(10) * c
    cercle(x, y, c/3, 'red')

##### Programme principal : ############

# Tâchez de bien "paramétrer" vos programmes, comme nous l'avons
# fait dans ce script. Celui-ci peut en effet tracer des damiers
# de n'importe quelle taille en changeant seulement la valeur
# d'une seule variable, à savoir la dimension des carrés :

c = 30 # taille des carrés

fen = Tk()
can = Canvas(fen, width =c*10, height =c*10, bg ='ivory')
can.pack(side =TOP, padx =5, pady =5)
b1 = Button(fen, text ='damier', command =damier)
b1.pack(side =LEFT, padx =3, pady =3)
b2 = Button(fen, text ='pions', command =ajouter_pion)
b2.pack(side =RIGHT, padx =3, pady =3)
fen.mainloop()#


Exercice 8.12 :

# Simulation du phénomène de gravitation universelle

from tkinter import *
from math import sqrt

def distance(x1, y1, x2, y2):
    "distance séparant les points x1,y1 et x2,y2"
    d = sqrt((x2-x1)**2 + (y2-y1)**2) # théorème de Pythagore
    return d

def forceG(m1, m2, di):
    "force de gravitation s'exerçant entre m1 et m2 pour une distance di"
    return m1*m2*6.67e-11/di**2 # loi de Newton

def avance(n, gd, hb):
    "déplacement de l'astre n, de gauche à droite ou de haut en bas"
    global x, y, step
    # nouvelles coordonnées :
    x[n], y[n] = x[n] +gd, y[n] +hb
    # déplacement du dessin dans le canevas :
    can.coords(astre[n], x[n]-10, y[n]-10, x[n]+10, y[n]+10)
    # calcul de la nouvelle interdistance :
    di = distance(x[0], y[0], x[1], y[1])
    # conversion de la distance "écran" en distance "astronomique" :
    diA = di*1e9 # (1 pixel => 1 million de km)
    # calcul de la force de gravitation correspondante :
    f = forceG(m1, m2, diA)
    # affichage des nouvelles valeurs de distance et force :
    valDis.configure(text="Distance = " +str(diA) +" m")
    valFor.configure(text="Force = " +str(f) +" N")
    # adaptation du "pas" de déplacement en fonction de la distance :
    step = di/10

def gauche1():
    avance(0, -step, 0)

def droite1():
    avance(0, step, 0)

def haut1():
    avance(0, 0, -step)

def bas1():
    avance(0, 0, step)

def gauche2():
    avance(1, -step, 0)

def droite2():
    avance (1, step, 0)

def haut2():
    avance(1, 0, -step)

def bas2():
    avance(1, 0, step)
    # Masses des deux astres :
    m1 = 6e24 # (valeur de la masse de la terre, en kg)
    m2 = 6e24 #
    astre = [0]*2 # liste servant à mémoriser les références des dessins
    x =[50., 350.] # liste des coord. X de chaque astre (à l'écran)
    y =[100., 100.] # liste des coord. Y de chaque astre
    step =10 # "pas" de déplacement initial

# Construction de la fenêtre :
fen = Tk()

fen.title(' Gravitation universelle suivant Newton')
# Libellés :
valM1 = Label(fen, text="M1 = " +str(m1) +" kg")
valM1.grid(row =1, column =0)
valM2 = Label(fen, text="M2 = " +str(m2) +" kg")
valM2.grid(row =1, column =1)
valDis = Label(fen, text="Distance")
valDis.grid(row =3, column =0)
valFor = Label(fen, text="Force")
valFor.grid(row =3, column =1)
# Canevas avec le dessin des 2 astres:
can = Canvas(fen, bg ="light yellow", width =400, height =200)
can.grid(row =2, column =0, columnspan =2)
astre[0] = can.create_oval(x[0]-10, y[0]-10, x[0]+10, y[0]+10,
                                fill ="red", width =1)
astre[1] = can.create_oval(x[1]-10, y[1]-10, x[1]+10, y[1]+10,
                                fill ="blue", width =1)
# 2 groupes de 4 boutons, chacun installé dans un cadre (frame) :
fra1 = Frame(fen)
fra1.grid(row =4, column =0, sticky =W, padx =10)
Button(fra1, text="<-", fg ='red',command =gauche1).pack(side =LEFT)
Button(fra1, text="->", fg ='red', command =droite1).pack(side =LEFT)
Button(fra1, text="^", fg ='red', command =haut1).pack(side =LEFT)
Button(fra1, text="v", fg ='red', command =bas1).pack(side =LEFT)
fra2 = Frame(fen)
fra2.grid(row =4, column =1, sticky =E, padx =10)
Button(fra2, text="<-", fg ='blue', command =gauche2).pack(side =LEFT)
Button(fra2, text="->", fg ='blue', command =droite2).pack(side =LEFT)
Button(fra2, text="^", fg ='blue', command =haut2).pack(side =LEFT)
Button(fra2, text="v", fg ='blue', command =bas2).pack(side =LEFT)

fen.mainloop()

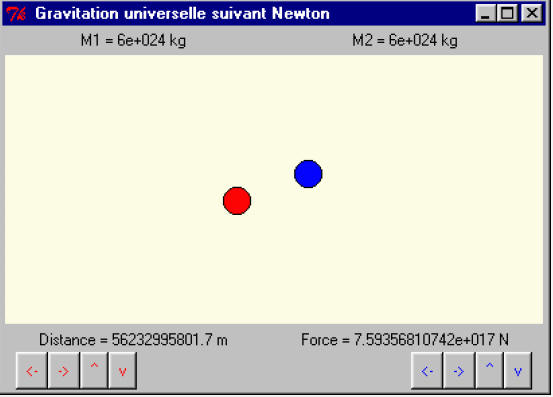
Exercice 8.16 :

# Conversions de températures Fahrenheit <=> Celsius

from tkinter import *

def convFar(event):
    "valeur de cette température, exprimée en degrés Fahrenheit"
    tF = eval(champTC.get())
    varTF.set(str(tF*1.8 +32))

def convCel(event):
    "valeur de cette température, exprimée en degrés Celsius"
    tC = eval(champTF.get())
    varTC.set(str((tC-32)/1.8))

fen = Tk()
fen.title('Fahrenheit/Celsius')

Label(fen, text='Temp. Celsius :').grid(row =0, column =0)
# "variable tkinter" associée au champ d'entrée. Cet "objet-variable"
# assure l'interface entre TCL et Python (voir notes, page 165) :
varTC =StringVar()
champTC = Entry(fen, textvariable =varTC)
champTC.bind("<Return>", convFar)
champTC.grid(row =0, column =1)
# Initialisation du contenu de la variable tkinter :
varTC.set("100.0")

Label(fen, text='Temp. Fahrenheit :').grid(row =1, column =0)
varTF =StringVar()
champTF = Entry(fen, textvariable =varTF)
champTF.bind("<Return>", convCel)
champTF.grid(row =1, column =1)
varTF.set("212.0")

fen.mainloop()

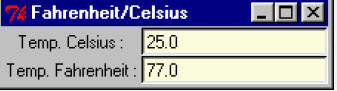
Exercice 8.18 à 8.20 :

# Cercles et courbes de Lissajous

from tkinter import *
from math import sin, cos

def move():
    global ang, x, y
    # on mémorise les coordonnées précédentes avant de calculer les nouvelles :
    xp, yp = x, y
    # rotation d'un angle de 0.1 radian :
    ang = ang +.1
    # sinus et cosinus de cet angle => coord. d'un point du cercle trigono.
    x, y = sin(ang), cos(ang)
    # Variante déterminant une courbe de Lissajous avec f1/f2 = 2/3 :
    # x, y = sin(2*ang), cos(3*ang)
    # mise à l'échelle (120 = rayon du cercle, (150,150) = centre du canevas)
    x, y = x*120 + 150, y*120 + 150
    can.coords(balle, x-10, y-10, x+10, y+10)
    can.create_line(xp, yp, x, y, fill ="blue") # trace la trajectoire

ang, x, y = 0., 150., 270.
fen = Tk()
fen.title('Courbes de Lissajous')
can = Canvas(fen, width =300, height=300, bg="white")
can.pack()
balle = can.create_oval(x-10, y-10, x+10, y+10, fill='red')
Button(fen, text='Go', command =move).pack()

fen.mainloop()

Exercice 8.27 :

# Chutes et rebonds
from tkinter import *

def move():
    global x, y, v, dx, dv, flag
    xp, yp = x, y # mémorisation des coord. précédentes
    # déplacement horizontal :
    if x > 385 or x < 15 : # rebond sur les parois latérales :
        dx = -dx # on inverse le déplacement
x = x + dx
# variation de la vitesse verticale (toujours vers le bas):
v = v + dv
# déplacement vertical (proportionnel à la vitesse)
y = y + v
if y > 240: # niveau du sol à 240 pixels :
    y = 240 # défense d'aller + loin !
    v = -v # rebond : la vitesse s'inverse
# on repositionne la balle :
can.coords(balle, x-10, y-10, x+10, y+10)
# on trace un bout de trajectoire :
can.create_line(xp, yp, x, y, fill ='light grey')
# ... et on remet ça jusqu'à plus soif :
if flag > 0:
    fen.after(50,move)

def start():
    global flag
    flag = flag +1
    if flag == 1:
    move()

def stop():
    global flag
    flag =0

# initialisation des coordonnées, des vitesses et du témoin d'animation :
x, y, v, dx, dv, flag = 15, 15, 0, 6, 5, 0

fen = Tk()
fen.title(' Chutes et rebonds')
can = Canvas(fen, width =400, height=250, bg="white")
can.pack()
balle = can.create_oval(x-10, y-10, x+10, y+10, fill='red')
Button(fen, text='Start', command =start).pack(side =LEFT, padx =10)
Button(fen, text='Stop', command =stop).pack(side =LEFT)
Button(fen, text='Quitter', command =fen.quit).pack(side =RIGHT, padx =10)

fen.mainloop()

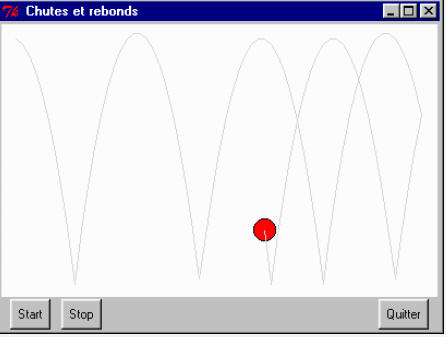
Exercice 8.33 (Jeu du serpent)

Nous ne fournissons ici qu’une première ébauche du script : le principe d’animation du « serpent ». Si le cœur vous en dit, vous pouvez continuer le développement pour en faire un véritable jeu, mais c’est  du travail !

from tkinter import *

# === Définition de quelques gestionnaires d'événements :
def start_it():
    "Démarrage de l'animation"
    global flag
    if flag ==0:
    flag =1
    move()

def stop_it():
    "Arrêt de l'animation"
    global flag
    flag =0

def go_left(event =None):
    "déplacement vers la gauche"
    global dx, dy
    dx, dy = -1, 0

def go_right(event =None):
    global dx, dy
    dx, dy = 1, 0

def go_up(event =None):
    "déplacement vers le haut"
    global dx, dy
    dx, dy = 0, -1

def go_down(event =None):
    global dx, dy
    dx, dy = 0, 1

def move():
    "Animation du serpent par récursivité"
    global flag
    # Principe du mouvement opéré : on déplace le carré de queue, dont les
    # caractéristiques sont mémorisées dans le premier élément de la liste
    # <serp>, de manière à l'amener en avant du carré de tête, dont les
    # caractéristiques sont mémorisées dans le dernier élément de la liste.
    # On définit ainsi un nouveau carré de tête pour le serpent, dont on
    # mémorise les caractéristiques en les ajoutant à la liste.
    # Il ne reste plus qu'à effacer alors le premier élément de la liste,
    # et ainsi de suite ... :
    c = serp[0] # extraction des infos concernant le carré de queue
    cq = c[0] # réf. de ce carré (coordonnées inutiles ici)
    l =len(serp) # longueur actuelle du serpent (= n. de carrés)
    c = serp[l-1] # extraction des infos concernant le carré de tête
    xt, yt = c[1], c[2] # coordonnées de ce carré
    # Préparation du déplacement proprement dit.
    # (cc est la taille du carré. dx & dy indiquent le sens du déplacement) :
    xq, yq = xt+dx*cc, yt+dy*cc # coord. du nouveau carré de tête
    # Vérification : a-t-on atteint les limites du canevas ? :
    if xq<0 or xq>canX-cc or yq<0 or yq>canY-cc:
        flag =0 # => arrêt de l'animation
        can.create_text(canX/2, 20, anchor =CENTER, text ="Perdu !!!",
                        fill ="red", font="Arial 14 bold")
    can.coords(cq, xq, yq, xq+cc, yq+cc) # déplacement effectif
    serp.append([cq, xq, yq]) # mémorisation du nouveau carré de tête
    del(serp[0]) # effacement (retrait de la liste)
    # Appel récursif de la fonction par elle-même (=> boucle d'animation) :
    if flag >0:
        fen.after(50, move)

# === Programme principal : ========

# Variables globales modifiables par certaines fonctions :

flag =0 # commutateur pour l'animation
dx, dy = 1, 0 # indicateurs pour le sens du déplacement

# Autres variables globales :
canX, canY = 500, 500 # dimensions du canevas
x, y, cc = 100, 100, 15 # coordonnées et coté du premier carré

# Création de l'espace de jeu (fenêtre, canevas, boutons ...) :
fen =Tk()
can =Canvas(fen, bg ='dark gray', height =canX, width =canY)
can.pack(padx =10, pady =10)
bou1 =Button(fen, text="Start", width =10, command =start_it)
bou1.pack(side =LEFT)
bou2 =Button(fen, text="Stop", width =10, command =stop_it)
bou2.pack(side =LEFT)

# Association de gestionnaires d'événements aux touches fléchées du clavier :
fen.bind("<Left>", go_left) # Attention : les événements clavier
fen.bind("<Right>", go_right) # doivent toujours être associés à la
fen.bind("<Up>", go_up) # fenêtre principale, et non au canevas
fen.bind("<Down>", go_down) # ou à un autre widget.

# Création du serpent initial (= ligne de 5 carrés).
# On mémorisera les infos concernant les carrés créés dans une liste de listes :
serp =[] # liste vide
# Création et mémorisation des 5 carrés : le dernier (à droite) est la tête.
i =0
while i <5:
    carre =can.create_rectangle(x, y, x+cc, y+cc, fill="green")
    # Pour chaque carré, on mémorise une petite sous-liste contenant
    # 3 éléments : la référence du carré et ses coordonnées de base :
    serp.append([carre, x, y])
    x =x+cc # le carré suivant sera un peu plus à droite
    i =i+1

fen.mainloop()