Graphiques et diagrammes usuels

Les graphes et les diagrammes sont une représentation imagée de données (numériques...) ou de schémas d'organisation. Il existe un grand nombre de représentations possibles, beaucoup sont accessibles à des non-techniciens ou des non-spécialistes. De nombreux logiciels offrent une assistance pour le tracé des graphes usuels.

Les techniciens et les ingénieurs les utilisent pour l'analyse (calculs techniques, détermination de paramètres expérimentaux, prévisions, coûts, organisation, etc.) et pour la communication (information, publicité, séminaires, etc.). Ils présentent avec précision et clarté un large éventail de données tout en mettant en valeur les informations principales.

Contrairement aux tableaux de données, ils permettent d'apprécier et observer plus facilement certaines caractéristiques essentielles : tendances, irrégularités, fluctuations, périodicités, rapports entre paramètres...

I - Graphes avec axes de coordonnées

D'origine mathématique, ils sont parfaitement adaptés à la description des phénomènes de type physique ou technique, notamment lorsqu'on souhaite connaître la variation d'une grandeur ou un paramètre important (température, force, coût...) en fonction d'un autre (temps, course... ) encore appelée variable.

1. Graphe à deux variables

Par convention le paramètre important est porté en ordonnée, « axe des y », et la variable, qui doit être indépendante du paramètre important, en abscisse, « axe des x ».

1. Axes, unités, courbe, variables, échelles : origine des systèmes d'axes à deux coordonnées.	2. Les quatre quadrants

Remarque : plusieurs courbes peuvent être tracées sur un même graphe ; c'est le cas de grandeurs de même famille utilisant la même échelle. De même, s'il n'y a pas risque de confusion ou de surcharge, une deuxième ordonnée peut être ajoutée à droite du graphe (flg. 4).

Cas des graphes à plus de deux variables : l'utilisation de familles de courbes permet d'ajouter une ou plusieurs variables supplémentaires et ainsi multiplier les possibilités de ce type de graphe.

3. Graphe à deux axes permettant de travailler avec plus de deux variables.	4. Graphe utilisant deux ordonnées pour représenter deux  familles de courbes.

2. Choix des échelles

Ce choix est de première importance : l'allure du graphe, son centrage, sa lecture et son exploitation en dépendent.

Un mauvais choix peut rendre difficile ou imprécise la lecture des données et ne pas mettre, en valeur (ou exagérer) les variations essentielles.

On peut, au besoin, modifier ou recentrer un graphe en changeant l'une des deux échelles.

5. Modification ou recentrage d'un graphe en changeant les échelles.

6. Principe du recentrage d'un graphe par modification des échelles.

7. Modification de l'allure du graphe en modifiant l'origine
et l'échelle sur l'un des axes.

3. Remarques et suggestions pour construire un graphe

 - Indiquer clairement le titre ou la référence du graphe.

- Sur chaque axe écrire lisiblement le nom de la grandeur utilisée ou son symbole normalisé.

- Pour chaque échelle indiquer l'unité de mesure normalisée choisie.

- Choisir les échelles de façon à ce que les courbes ne soient pas comprimées ; la courbe représentative doit être centrée dans le plan du graphique et dessinée avec précision.

- Choisir de préférence des échelles pleines (origine à zéro). Une modification de l'origine peut amplifier des variations lorsque celles-ci sont faibles ; cette représentation peut parfois être imprécise et influencer le jugement.

- Habituellement, les échelles sont croissantes en allant de la gauche vers la droite (axe des x) et de bas en haut (axe des y).

- Écrire généralement les chiffres des échelles en dehors des zones graphiques.

- Limiter le nombre des décimales, à cette fin utiliser les puissances de 10 (par exemple remplacer 10 000 000 par 10⁷).

- Faire éventuellement un cadre pour délimiter la zone graphique.

8. Exemples d'écriture sur l'axe des ordonnées.

9. Exemple d'écriture sur l'axe des abscisses.

4. Courbe observée, courbe expérimentale et courbe mathématique

Courbe observée :

surtout utilisée comme outil de communication, elle est tracée à partir de données connues, point par point, sans interpolation. Elle permet de faire un bilan récapitulatif et de dégager des tendances générales.

Courbe expérimentale :

servant essentiellement comme outil d'analyse, elle est obtenue par interpolation (courbe moyenne) à partir d'une série de mesures en laboratoire ou sur le terrain. Les points tracés peuvent utiliser des symboles ou des couleurs différents pour différencier les séries de mesures.

Courbe mathématique :

elle est obtenue par calcul à partir d'une équation connue. C'est une courbe théorique et les points calculés ne sont pas, en principe, dessinés sur le graphe.

10. Courbe observée.	11. Courbe expérimentale.	12. Courbe mathématique.

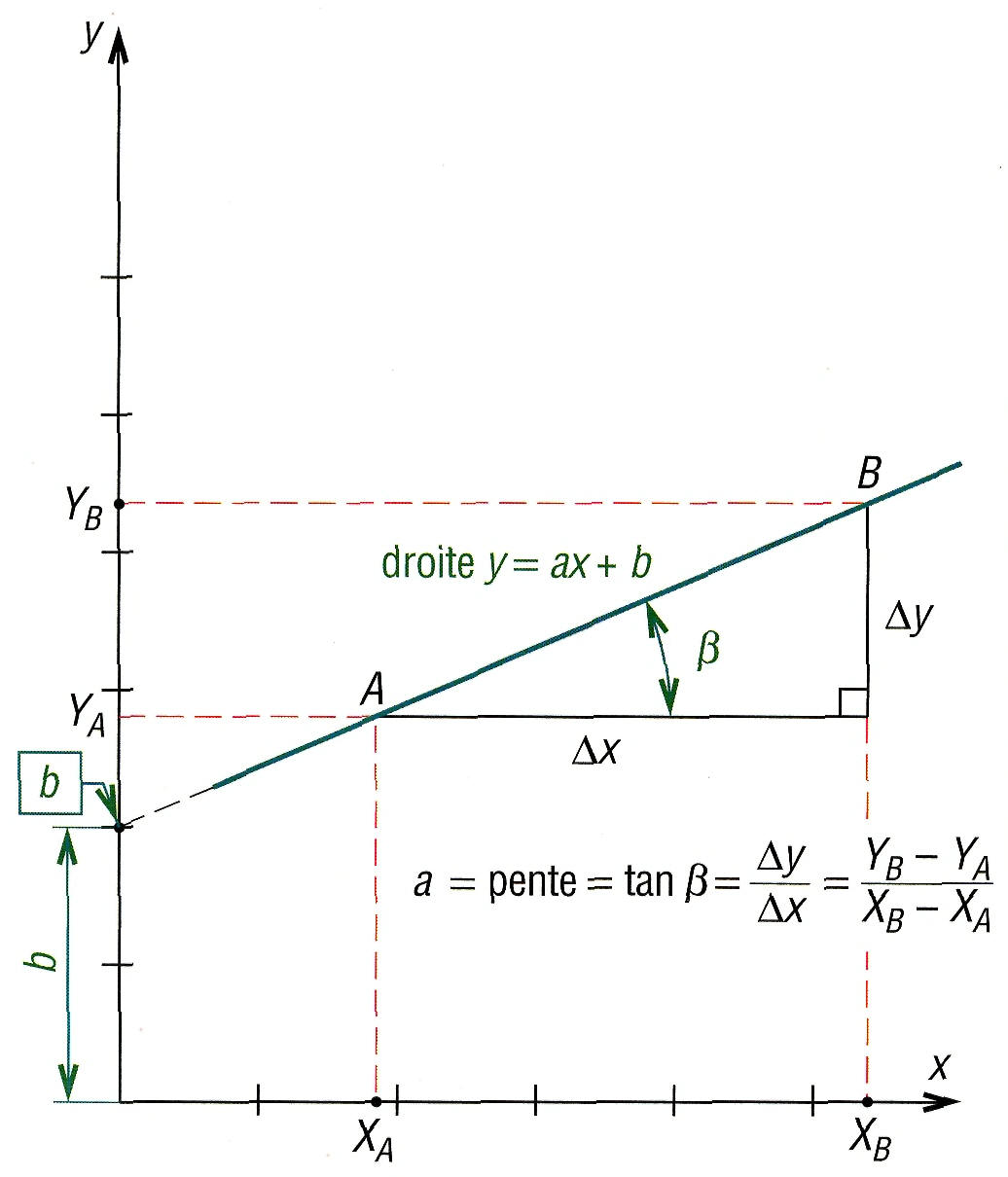
5. Courbes ou droites de la forme y = ax+b

Quelle que soit la valeur des constantes a et b, il y a toujours proportionnalité entre les deux variables x et y. Autrement dit, quels que soient les points A et B choisis, l'accroissement de V (« Y_B - Y_A ») est toujours proportionnel à l'accroissement de X ( « X_B - X_A »).

Remarque : a, pente de la droite, caractérise la proportionnalité ; b est l'ordonnée du point d'intersection entre la droite et l'axe des y (pour x =0, y = b).

13. Principaux paramètres liés aux droites y = ax + b.	14. Exemple de droites de forme y = ax + b.

6. Courbes en puissance de X du type Y = A.(X)ⁿ

a) Allures générales

A et n sont des constantes (paramètres constants), n est la puissance de X.

- Si n = 0 et n = 1 les courbes obtenues sont des droites.

- Si n = 2 la courbe est une parabole.

- Si n = -1 la courbe est une hyperbole.

15. Exemples de courbes d'équation y = xⁿ.

Remarques : si n >1 les graphes obtenus sont symétriques par rapport à l'axe y. Si 0 < n <1 les graphes sont symétriques par rapport à l'axe x.

b) Transformation des graphes Y=A.(X)ⁿ en droite (linéarisation)

Les graphes n'étant pas toujours facilement exploitables expérimentalement avec les axes usuels, échelles arithmétiques, il est possible de les transformer en expression linéaire (droite) à partir des logarithmes.

Principe (lg étant le logarithme décimal) :

V = A(X)ⁿ donne

lg Y=lg [A(X)ⁿ] = lgA + n.lgX

Posons lg Y = y ; lg A = a et n.lg X = n.x

on obtient y = a + n.x

y = a + n.x est l'équation d'une droite dans le système d'axes (x, y) ou [lg X, lg Y] avec échelles logarithmiques (papier « log-log » pour les tracés).

16. Papier log-log.	17. Courbes y = xn tracées sur papier log-log.

Intérêt expérimental des graphes avec échelles log-log :

si au cours d'une expérimentation, avec série de mesures et report des valeurs sur un graphe log-log, la courbe obtenue est une droite, on peut affirmer que le phénomène étudiée est du type Y = A (X)ⁿ. La valeur de n est obtenue en mesurant (sur le graphe) la pente de la droite et celle de A en mesurant l'ordonnée du point d'intersection entre la droite et l'axe y.

7. Courbes exponentielles du type Y= A(e)^nX ou Y= A(B)^x

a) Allures générales

Leur croissance est beaucoup plus rapide que celles du type Y = A(X)ⁿ.

18. Exemples de courbes d'équation y = e^nx

b) Linéarisation

En utilisant les logarithmes, les courbes exponentielles peuvent être transformées en droite (linéarisation) pour une exploitation expérimentale plus facile. Deux cas peuvent se présenter, ln étant le logarithme népérien :

Cas B = 10 :

lg étant le logarithme décimal,

Y = A(B)^x donne

lg Y = lg A + X.lg 10 = lg A+X

forme y = a + X

y = a + X est une droite dans le système d'axes [y, X] ou [lg Y, X] (échelle logarithmique en ordonnée et échelle arithmétique en abscisse). Il suffit d'utiliser un papier semi-logarithmique (log. décimal) pour faire les tracés. Pour les exemples proposés Y = 10^nX devient y = 1 + nX avec a = lg 10 = 1.

Cas B différent de 10 :

posons B = eⁿ

(e = 2,71828 = nombre d'Euler et n paramètre de croissance)

Y = A(e)^nX donne

In Y = In A + nX. In e (avec In e = 1)

forme y = a + nX

C'est l'équation d'une droite dans une grille semi-logarithmique (avec log. népérien).

Intérêt expérimental :

dans les deux cas, si au cours d'une expérimentation et après report des points, la courbe obtenue est une droite en grille semi-log, on peut affirmer que le phénomène étudié est du type exponentiel.

La valeur de n est obtenue en mesurant, sur le graphe, la pente de la droite et celle de A en mesurant l'ordonnée du point d'intersection entre la droite et l'axe y.

19. Papier semi-logarithmique.	20. Courbes de la forme y = enx tracées en papier semi-log.

8. Graphes en coordonnées polaires

D'applications diverses, ils sont obtenus par des systèmes d'enregistrement à disque.

Deux variables : la distance r (>0 ou <0) mesurée suivant une droite OP et l'angle orienté θ (téta) mesuré entre l'axe des x et OP.

Principe et courbes usuelles

21. Coordonnées polaires et exemples de graphes.

Exemples expérimentaux :

22. Graphe donnant la valeur du bruit autour d'une automobile.	23. Graphe de circularité d'un roulement à billes.

9. Graphes triangulaires à trois variables

Ils sont plutôt utilisés en métallurgie et en chimie.

Cas d'emploi :

- Comparaison de trois variables apparentées ou non indépendantes (par exemple dont la somme «100 % » est toujours constante).

- Analyse de compositions ou de structures à l'aide d'un réseau de courbes...

24. Principe 1	25. Principe 2	26. Exemple

II - Graphiques ou diagrammes à barres

Ils sont facilement accessibles au plus grand nombre, techniciens et non-techniciens. Les livres, revues, magazines et journaux de grande diffusion les utilisent couramment.

Principe :

dans ces diagrammes, les valeurs numériques (quantités produites, pourcentages, coûts, prix...) sont représentées graphiquement par des barres dont la longueur est proportionnelle à la quantité. Les barres, verticales ou horizontales, sont placées à intervalles réguliers. Les combinaisons possibles sont multiples.

Utilisations usuelles :

- Présentation de données à des non-techniciens (faciles à lire et à comprendre).

- Comparaison simple de deux données.

- Comparaison de données sur une période de temps.

- Donner une image de plusieurs données en rapport les unes avec les autres.

Remarque : ils sont moins intéressants lorsqu'il faut comparer un grand nombre de valeurs ou dans le cas de séries de données.

1. Principaux diagrammes à barres verticales

Diagramme à barres simples :

il est utilisé pour suivre l'évolution d'une donnée ou grandeur (ventes, productions, coûts...) en fonction d'une variable (temps, lieu...).

27. Diagramme à barres simples.

Diagramme à barres groupées :

il permet de comparer les évolutions de plusieurs grandeurs (données) différentes, toutes fonction d'une même variable (temps...). Chaque grandeur doit être identifiée par une couleur ou un motif particulier (défini en annexe par une clé ou une légende).

28. Diagramme à barres groupées.

Diagramme à barres subdivisées :

il est employé pour comparer plusieurs grandeurs (données) différentes toutes fonctions d'une même variable, tout en suivant l'évolution de leur somme ou total. Chaque grandeur doit être identifiée par une couleur ou un motif différent, défini en annexe par une clé ou une légende.

29. Diagramme à barres subdivisées.	30. Variante à barres subdivisées.	31. Variante à barres subdivisées.

Histogrammes :

ce sont des diagrammes à barres verticales particuliers utilisés pour représenter la répartition statistique d'une série de mesures concernant une même grandeur et pour analyser les caractéristiques d'une population (rapide vue d'ensemble, valeur moyenne, dispersion ou étalement, tendances, comportement...)

Le principal problème est le choix du nombre des intervalles compte tenu du nombre des mesures ou observations (voir les recommandations d'Ishikawa)

	32. Histogramme de répartition de temps d'usinage.

2. Diagrammes à barres horizontales

C'est une variante des précédents souvent utilisée lorsque l'une des grandeurs représentées est beaucoup plus grande que les autres.

Propriété :

cette présentation, à visualisation identique, permet d'utiliser des barres moins larges et des espacements (intervalles) plus étroits : graphes plus compacts à qualité de lecture identique.

Principaux cas :

barres simples, barres groupées, barres subdivisées, barres dos-à-dos (variantes des barres subdivisées), pyramide des âges (sorte d'histogramme).

33. Diagramme à barres simples horizontales.	34. Variante avec effet de perspective.	35. Diagramme à barres groupées horizontales.
36. Barres groupées dos-à-dos.	37. À barres dos-à-dos de même longueur.	38. Pyramide des âges des lave-linges.

III - Diagrammes type camembert

Ils sont souvent utilisés pour visualiser et comparer facilement les proportions (pourcentages) de plusieurs grandeurs ; un demi-camembert peut suffire à un nombre réduit de paramètres. Les variantes en perspective permettent d'ajouter des subdivisions supplémentaires.

Pour un camembert :

1 % occupe 3,6° ; 10 % occupe 36° ; X % occupe X fois 3,6°.

Pour un demi camembert : 1 % occupe 1,8° ; 10 % occupe 18° ; X % occupe X fois 1,8°.

39. Diagramme camembert.	40. Demi-camembert.	41. Camembert avec effet de perspective.

IV - Graphes rectangulaires avec surfaces

Ils combinent à la fois les propriétés des diagrammes à barres et celles des graphes à coordonnées rectangulaires du paragraphe 1.

Ils ont le même rôle que les diagrammes à barres subdivisées en offrant des comparaisons plus détaillées.

L'utilisation de couleurs ou de motifs différents simplifie la lecture.

42. Diagrammes à surfaces en coordonnées rectangulaires.

V-Abaques

Principal objectif :

les abaques éliminent les calculs fastidieux nécessaires à l'exploitation de certaines formules de type mathématique, complexes, connues et contenant trois variables ou plus. Les abaques exigent du temps pour être construits mais sont très pratiques et très sûrs à l'usage ; il y a peu d'erreurs d'exploitation.

Principe :

ils consistent en un jeu de trois échelles, ou plus, graduées (arithmétique, logarithme. ..), verticales ou inclinées, droites ou courbes représentant graphiquement les variables de la formule.

La valeur inconnue (cherchée) est déterminée par alignement. Dans le cas de trois variables, une droite (isopleth), tracée à partir des deux variables connues, coupe l'échelle de la troisième à la valeur cherchée.

Principales formes d'abaques

43. Différents types d abaques.

VI - Organigrammes

II existe une grande diversité de représentations possibles. Les organigrammes permettent de décrire des organisations, des processus, des ressources humaines, des produits, des flux de données...

Ce sont des outils particulièrement puissants et appréciés dans la mesure où ils présentent une très grande souplesse : pas de règles rigides ni de formalisme lourd ou complexe. De plus, ils sont faciles à comprendre par le plus grand nombre, techniciens ou non, spécialistes ou non.

Une personnalisation éventuelle du graphisme et de l'écriture est souvent possible (logiciels...).

1. Organigrammes - Arborescences

Ce sont des sortes de tableaux représentant la structure hiérarchique d'une entreprise, d'un organisme, d'un système, d'un produit...

Organigramme de ressources humaines :

il représente et détaille la structure hiérarchique d'une société. Les niveaux de responsabilité ou d'importance se retrouvent en allant du haut vers le bas. Le nom des personnes, leur fonction et les renseignements jugés importants (téléphone, fonction occupée...) sont indiqués dans un même rectangle ou boîte.

Les relations ou rapports directs existant entre ces personnes sont représentés par les lignes, verticales et horizontales, fléchées ou non, tracées entre les boîtes.

44. Organigramme de forme générale pour organisation, ressources humaines...

Organigramme technique de produit (ou arborescence technique) :

c'est une variante du précédent, adaptée à la description d'un produit. Il représente la structure hiérarchique du produit en partant de l'ensemble (système global) et en s'arrêtant aux plus petits éléments ou composants (le produit est décortiqué niveau par niveau).

45. Organigramme technique de produit (OTP) ; forme générale.

Arborescence fonctionnelle :

utilisée en analyse fonctionnelle pour décrire les différentes fonctions liées à un produit, elle permet de représenter, à partir d'une fonction de base ou principale, les fonctions qui, de niveau en niveau, participent à celle-ci ou la réalisent.

46. Arborescence fonctionnelle d'un système de transport.

Arbre ou graphe de fonctions :

également utilisé en analyse fonctionnelle, ils permettent d'analyser la nature et le poids des liaisons des fonctions techniques entre elles et avec les fonctions de service ou principales.

- Fp1: fonction principale ;

- Ft1, Ft2: sous-fonction principale de niveau 1 ;

- Ft11, Ft21 : sous-fonction principale de niveau 2 ;

-Ft111, Ft112, Ft113... : fonctions techniques successives de même niveau...

47. Exemple d'arbre de fonctions.

2. Algorigrammes, ordinogrammes...

Organigrammes particuliers avec règles d'écriture et d'évolution (boîtes particulières, lignes fléchées pour le sens du flux...), ils sont utilisés pour représenter la logique d'enchaînement d'un algorithme ou des opérations de traitement d'un problème, d'un flux de données.

48. Principaux symboles.

Principaux cas d'évolutions entre boîtes

49. Séquence simple.	50. Embranchement entre deux séquences.	51. Reprise d'étapes.
52. Boucle de reprise avec test initial.	53. Exemple avec boucles emboîtées.	54. Saut d'étapes.

Algorithme : c'est l'ensemble des règles opératoires propres à un calcul ou à l'enchaînement des actions nécessaires à l'accomplissement d'une tâche.

VIII - Exercices

Exercice 1

Tracer un graphe, en coordonnées rectangulaires avec deux axes à échelles arithmétiques, représentant les données suivantes (production en ordonnée) :

a) Déterminer l'équation de la droite décrivant au plus près ces données.

b) Quelle production peut-on envisager pour 1995 ?

Exercice 2

La flèche (f) d'un ressort de traction à spires en fonction de la charge (F) est mesurée expérimentalement. Les résultats sont :

a) Tracer le graphe F fonction de f. Déterminer l'équation correspondante ; en déduire la raideur du ressort.

b) Quelle force produira une flèche de 70 mm ?

Exercice 3

Afin de réaliser l'étalonnage d'un thermocouple fer-constantan on détermine expérimentalement les données suivantes :

a) Tracer le graphe T fonction de la f.é.m. (force électromotrice). Déterminer l'équation de la droite approchant au plus près ces données.

b) Quelle est la valeur de la f.é.m. pour 1 000 °C ?

Exercice 4

On observe la chute d'un objet lâché du haut d'un gratte-ciel. La hauteur de chute et le temps correspondant sont rassemblés ci-dessous :

a) L'équation représentant la chute est de la forme [h = a.tn]. Déterminer les paramètres constants a et n après linéarisation et tracé sur papier log-log.

b) Quelle est la durée de la chute si la hauteur du gratte-ciel est de 250 m ?

Exercice 5

La capacité (C) d'une vis d'Archimède, utilisée pour le convoyage des graines de maïs, dépend de sa vitesse de rotation (N). Les mesures réalisées expérimentalement donnent :

Tracer les données sur un papier log-log, en déduire 1 équation exprimant la capacité de la vis en fonction de sa vitesse. Quelle est la capacité à 250 tr/min ?

Exercice 6

La consommation d'essence (Q) d'une automobile en fonction de sa vitesse (V) est mesurée expérimentalement. Les résultats sont :

L'équation entre Q et v a la forme exponentielle [Q = a.e^nx. Déterminer, après linéarisation et tracé des données sur papier semi-log la valeur des paramètres constants a et n. Quelle est la consommation prévisible à 300 km/h ?

Exercice 7

Le chiffre d'affaires d'un composant nouvellement lancé sur le marché est relevé mois après mois. Les données sont :

a) L'équation liant les deux variables a la forme exponentielle [Y = a.e^nX]. Déterminer les paramètres constants a et n.

b) Quel est le chiffre d'affaires prévisible pour juillet ?

Le tableau suivant est utilisé pour les exercice 8 à 13. Il rassemble les données statistiques essentielles de 1980 à 2005 d'une entreprise fabricant des composants pneumatiques.

Exercice 8

Tracer un histogramme donnant une représentation du nombre d'employés.

Exercice 9

Tracer un diagramme à barres représentant le nombre d'unités produites.

Exercice 10

Tracer un diagramme à barres groupées représentant le nombre d'unités produites avec le nombre d'employés.

Exercice 11

Tracer un diagramme à surfaces en coordonnées rectangulaires représentant les évolutions comparées du chiffre d'affaires et des coûts annuels. Mettre en évidence les bénéfices.

Exercice 12

Refaire l'exercice 11 précédent avec un diagramme à barres subdivisées.

Exercice 13

Tracer un diagramme camembert pour les données suivantes :

Exercice 14

Un essai de microphone directionnel fournit les données suivantes : 

La sortie en volts est mesurée à partir d'un source sonore constante déplacée de façon circulaire autour du micro. Il y a symétrie par rapport à la ligne (0°, 180°). Tracer les résultats sur un graphe avec coordonnées polaires.