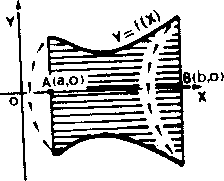
Volume d'un solide de rotation
Étant donnée la fonction continue y = f(x) définie en [a, b] avec f(x) ≥ 0, le volume du solide obtenu en faisant tourner d'un tour complet autour de l'axe x la courbe y = f(x) et compris entre les deux plans orthogonaux au plan cartésien qui passent par a et par b, est eprimé par :
| V = π· | ∫ | b | f(x)2 dx |
| a |