1. Méthode de substitution :

En résolvant (1) par rapport à y, on obtient :

En remplaçant (3) en (2), on obtient une équation avec x seulement :

donc on obtient :

et en remplaçant (5) en (3) on trouve :

Les formules (5) et (6) donnent les solutions x et y du système.

2. Méthode de comparaison :

En résolvant (1) et (2) en même temps par rapport à y on obtient :

or (3) = (7) donc

on obtient une équation en x seulement qui donne :

puis en remplaçant (5) en (3) ou en (7) on obtient la valeur de y :

3. Méthode de réduction (addition ou soustraction) :

En multipliant les deux termes de (1) par B₁ et ceux de (2) par -B, on obtient :

(8) | AB₁x + BB₁y = B₁C
(9) | -A₁Bx - BB₁y = -BC₁

En ajoutant membre à membre (8) + (9) on obtient :
AB₁x - A₁Bx = B₁C - BC₁

qui donne :

En remplaçant (5) en (1) ou en (2) on obtient la valeur de y :

4. Formule de Cramer :

En indiquant avec :

=	|	A	B	|	= AB1 - A1B
	|	A1	B1	|

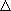
( déterminant du système)

x =	|	C	B	|	= B1C - BC1
	|	C1	B1	|

y =	|	A	C	|	= AC1 - A1C
	|	A1	C1	|

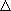
1. Si 0 AB₁ - A₁B 0 le système est déterminé, c'est à dire qu'il a une seule solution (couple ordonné de valeurs x, y)

2.	Si = 0 (AB1 - A1B = 0) et
	x 0 (B1C - BC1 0)
	y 0 (AC1 - A1C 0)
	le système n'admet pas de solution et il est dit impossible

3. Si = _x = _y = 0, le système admet une infinité de solutions et il est dit indéterminé.

 

 

 

 

 

Recherche personnalisée