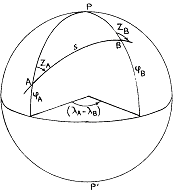
Distance à la surface d'une sphère

Distance à la surface d'une sphère

Comment obtenir la distance de deux points connus en longitude et en latitude sur une sphère ?

Si on considère deux points A et B sur la sphère, de latitudes respectives et φA et φB, et de longitudes respectives λA et λB, alors la distance angulaire s(AB) entre A et B est donnée par la formule :

s(AB) = arccos (sin(φA)sin(φB) + cos(φA)cos(φB)cos(λB - λA))

(s(AB) en radians)

Pour info :
A_{Z_A} = arcsin ((cos(φB)sin(λB - λA)) / sin(s))

A_{Z_B} = arcsin ((cos(φA)sin(λB - λA)) / sin(s))

(A_{Z_A} et A_{Z_B} en radians)

Pour connaître la distance S en mètres, il suffit de multiplier s(AB) par le rayon de la sphère.
(Si la sphère est la Terre, son rayon moyen vaut 6374892.5m)

Recherche personnalisée