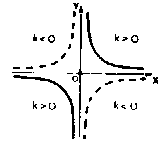
Hyperbole équilatérale par rapport aux asymptotes

Dans l'hyperbole équilatérale a = b et les asymptotes sont les bissectrices des quadrants.
En réalisant un changement d'axes et en prenant comme axes nouveaux les asymptotes de l'hyperbole, en faisant une rotation de -π/4 (-45°), l'équation de l'hyperbole équilatérale prend la forme de :

Si k > 0 : les branches de l'hyperbole sont dans le 1^er et 3^ème quadrant.
Si k < 0 : les branches de l'hyperbole sont dans le 2^ème et 4^ème quadrant.