Ellipse

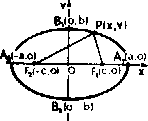
L'ellipse est le lieu géométrique des points du plan dont les distances de deux points fixes (F₁ et F₂), appelés foyers, ont une somme constante (= 2a).

Étant donné : F₁(c, 0)
                     F₂(-c, 0)
                     F₂F₁ = 2c
axe x sur la droite F₂F₁ et l'origine des axes sur le point au centre du segment F₁F₂ (centre de l'ellipse), l'équation de l'ellipse est :

ou bien :

b2x2 + a2y2 = a2b2

où

2a est le grand axe 2b est le petit axe b2 = a2 - c2

Excentricité de l'ellipse :
e = c / a
plus l'excentricité est grande et plus l'ellipse et aplatie.
Un cercle est une ellipse d'excentricité nulle.

Si le grand axe a est parallèle à l'axe y et le petit axe b est parallèle à l'axe x, l'équation de l'ellipse est :