 x
 = ||||·
||||· sin
θ·  |
0 ≤  ≤ π |
Produit vectoriel
On appelle produit vectoriel de deux vecteurs le vecteur :
| x
= ||||·
||||· sin
θ· |
0 ≤ ≤ π |
où est l'angle formé
par les directions des vecteurs
et
. et
est un verseur
perpendiculaire au plan de
et
de façon que
,
,
forment un système
orienté.
En utilisant les composantes cartésiennes des vecteurs, le produit vectoriel prend la forme :
| | | ax | | | bx | |||
|
x
= |
| | ay | x | | | by | = (aybz - azby)
- (axbz - azbx)
+ (axby - aybx) |
| | | az | | | bz |
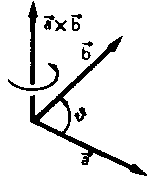
Pour le produit vectoriel, les propriétés suivantes sont valables :
x = -
x
x ( +
) =
x
+
x
(propriété
distributive)
NB : si deux vecteurs sont parallèles entre eux, le produit vectoriel est nul.
