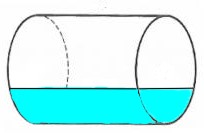
Calculer le volume d'eau en litre contenu dans un cylindre Horizontale.

MATHÉMATIQUES


 		V = π * r2 * L
V = volume en cm3
r = rayon en cm
L = la longueur du cylindre en cm
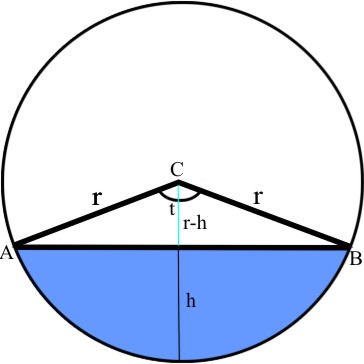
Trouver l'air du segment de cercle (En bleu) = A
V=  A * L

A = (π r2 t°/ 360) - ((r2/2) sin t°)

V = Volume en cm3      Volume en litre = V / 1000

A = Air du du segment

L = la longueur du cylindre en cm

r = rayon en cm

h = Hauteur du liquide en cm

t  = angle Téta en degré

A= (π * r2 * Téta / 360) - (r2 / 2 * sin Téta)

Pour trouver Téta

Le triangle  formé par les deux côtés r et le segment AB est composé de deux triangles rectangles. On a un triangle rectangle donc on connaît l'hypoténuse r et un côté r-h.

L'angle formé par r et r-h est égale à Téta / 2

cos (Téta / 2) = (r-h) / r = angle en degré     Téta = 2 * Acos ((r-h) / r) = angle en degré

A = (π r2 t°/ 360) - ((r2/2) sin t°)     V=  A * L = volume en cm3     Nombre de litre dans le cylindre = V / 1000

Le volume d'un réservoir d'essence en forme de cylindre ayant un rayon de 125 cm et une longueur de 297,1 cm est égale à:

V = π * r2 * L =  π * 1252 * 297,1 = 14583862 cm3     V en litre = 14583862 / 1000 = 14583,862

Pour savoir combien il y a de litres d'essence dans le réservoir on mesure la hauteur de l'essence avec une règle qui est perpendiculaire au centre du fond du réservoir (là où c'est le plus creux).

   

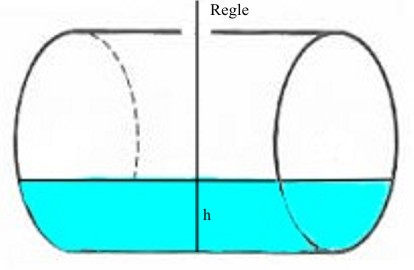
Pour h = 5 cm

r = 125 et  L  = 297,1        r-h = 125 - 5 = 120   

Téta (t°)= 2 * Acos((r-h) / r  = 2 * Acos(120 / 125) = 32,52 degré

A = (π r2 t°/ 360) - ((r2/2) sin t°)  = (π * 1252 * 32,52 / 360) - ((1252 / 2) * sin (32,52)  = 4434,23- 4199,95 = 234,28

V=  A * L  = 234,28 * 297,1 = 69604,59 cm3     Nombre de litre dans le cylindre = V / 1000 = 69,61 litres

Excel

Les fonctions trigonométriques d'Excel utilisent que des angles en Radian.

La fonction Acos retourne l'angle en Radian, on doit le convertir en degré.

L'angle de la fonction Sin doit être en radian.

Donc on doit calculer l'angle Téta en degré TD et en radian TR.

TR = 2 * Acos((r-h) / r)

TD = TR * 180 / π

Formule Excel

$D$6 = Rayon

$D$7 = Longueur

A11 = Hauteur

Copier cette formule:

=(($D$6*$D$6*PI()*(2*DEGRES(ACOS(($D$6-A11)/$D$6)))/360)-($D$6*$D$6/2*SIN(2*ACOS(($D$6-A11)/$D$6))))*$D$7/1000

où

TD = 2*DEGRES(ACOS(($D$6-A11)

TR = 2*ACOS(($D$6-A11)/$D$6)

A =  (($D$6*$D$6*PI()*(2*DEGRES(ACOS(($D$6-A11)/$D$6)))/360)-($D$6*$D$6/2*SIN(2*ACOS(($D$6-A11)/$D$6))))

V = (($D$6*$D$6*PI()*(2*DEGRES(ACOS(($D$6-A11)/$D$6)))/360)-($D$6*$D$6/2*SIN(2*ACOS(($D$6-A11)/$D$6))))*$D$7/1000

Fonction VBA

Function volcylcou(rayon, longueur, hauteur)

    TD = (Application.Acos((rayon - hauteur) / rayon) * 180 / Application.Pi()) * 2
    TR = (Application.Acos((rayon - hauteur) / rayon)) * 2
    Aire = (Application.Pi() * rayon * rayon * TD / 360) - ( rayon * rayon / 2 * Sin(TR))
    volcylcou = Aire * longueur / 1000

End Function

Cellules Nommées

=((Ra*Ra*PI()*(2*DEGRES(ACOS((Ra-A11)/Ra)))/360)-(Ra*Ra/2*SIN(2*ACOS((Ra-A11)/Ra))))*Long/1000

Ra = $D$6

Long = $D$7

 

Fichier Excel : CVOLUME1.XLS