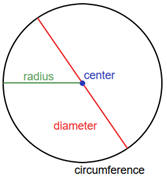
Circle, Square and Rectangle formula

Circle, Square and Rectangle formula

Circle

d = 2r r = d/2

C = 2πr C = πd C = 2√πA

A = πr² A = πd² / 4 A = C² / 4π

Square

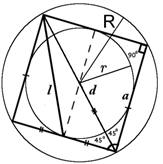
Diagonal of the square formula from

				diameter		diameter	length
side	area	perimeter	circumradius	of the circumcircle	the inradius	of the incircle	of the segment l
d = a·√2	d = √2A	d = P / 2√2	d = 2R	d = Dc	d = 2r√2	d = Di√2	d = l (2√10/5)

Perimeter of a square formulas from

				diameter		diameter	length
side	area	diagonal	circumradius	of the circumcircle	the inradius	of the incircle	of the segment l
P = 4a	P = 4√A	P = 2d√2	P = 4R√2	P = 2Dc√2	P = 8r	P = 4Di	P = l (8√5)

Area of a square formulas from

				diameter		diameter	length
side	perimeter	diagonal	circumradius	of the circumcircle	the inradius	of the incircle	of the segment l
A = a²	A = P²/16	A = d² / 2	A = 2R²	A = Dc² / 2	A = 4r²	A = Di²	A = l ²(16√5)

Circumradius of a square formulas from

				diameter		diameter	length
side	perimeter	diagonal	area	of the circumcircle	the inradius	of the incircle	of the segment l
R = a √2 / 2	R = P / 4√2	R = d / 2	R = √2A / 2	R =Dc / 2	R = r √2	R = Di √2 / 2	R = l √10/5

inscribed circle of a square formulas from

				diameter		diameter	length
side	perimeter	diagonal	area	of the circumcircle	circumradius	of the incircle	of the segment l
r = a / 2	r = P / 8	r = d / 2√2	r = √A / 2	r = Dc / 2√2	r = R / √2	r = Di / 2	r = l / √5

Rectangle

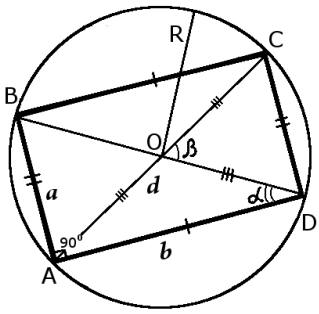
Rectangle sides from

diagonal	area	perimeter
and rectangle side	and rectangle side	and rectangle side	diagonal	diagonal
a = √(d² - b²)	a = A / b	a = (P - 2b) / 2	a = d sinα	a = d sin β / 2
b = √(d² - a²)	b = A / a	b = (P - 2a) / 2	b = d cosα	b = d cos β / 2

Diagonal of a rectangle from

			radius of the	diameter of the
	area	perimeter	escribed circle	escribed circle
rectangle sides	and rectangle side	and rectangle side	(excircle)	(excircle)
d = √(a² + b²)	d = √(A² + a⁴⁾ / a	d = √(P² - 4Pa + 8a²) / 2	d = 2R	d = Dc
	d = √(A² + b⁴⁾ / b	d = √(P² - 4Pb + 8b²) / 2

sine of the angle that adjacent		cosine of the angle that adjacent
to the diagonal		to the diagonal		sine of the acute angle between
and the opposite side of the angle		and the opposite side of the angle		the diagonals and the area
d = a / sin α		d = c / cos α		d = √2A / sin β

Perimeter of a rectangle from

			radius of the	diameter of the
	area	diagonal	escribed circle	escribed circle
rectangle sides	and rectangle side	and rectangle side	(excircle)	(excircle)
P = 2a + 2b	P = (2A + 2a²) / a	P = 2(a + √(d² - a²))	P = 2(a + √(4R² - a²))	P = 2(a + √(Dc² - a²))
	P = (2A + 2b²) / b	P = 2(b + √(d² - b²))	P = 2(b + √(4R² - b²))	P = 2(b + √(Dc² - b²))

Area of a rectangle

			radius of the	diameter of the
	perimeter	diagonal	escribed circle	escribed circle
rectangle sides	and rectangle side	and rectangle side	(excircle)	(excircle)
A = a · b	A = (Pa - 2a²) / 2	A = a√(d² - a²)	A = a√(4R² - a²)	A = a√(Dc² - a²)
	A = (Pb - 2b²) / 2	A = b√(d² - b²)	A = b√(4R² -b²)	A = b√(Dc² - b²)

	sine of the acute angle between
	the diagonals and the area
	A = d² · sin β / 2

An angle between the diagonal and rectangle side

		sin α = a / d	cos α = b / d	α = β / 2


An angle between the rectangle diagonals

		β = 2α	sin β = 2A / d²

		Inradius
		Ri = a / 2


Circumradius of a rectangle from

				diameter of the
	perimeter	area		escribed circle
rectangle sides	and rectangle side	and rectangle side	diagonal	(excircle)
R = √(a² + b² ) / 2	R = √(P² - 4Pa + 8a²) / 4	R = √(AS² + a⁴) / 2a	R = d / 2	R = Dc / 2
	R = √(P² - 4Pb + 8b²) / 4	R = √(AS² + b⁴) / ba

sine of the angle that adjacent		cosine of the angle that adjacent
to the diagonal		to the diagonal		sine of the acute angle between
and the opposite side of the angle		and the opposite side of the angle		the diagonals and the area
R = a / 2sin α		R = b / 2cos α		R = √(2A / sin β) / 2

Recherche personnalisée