Le système de trois équations avec trois inconnues a la forme générale :

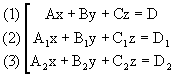
1. Méthode de substitution : on peut résoudre (1) par rapport à z et remplacer la valeur trouvée de z en (2) et (3) qui auront ainsi les seules inconnues x et y. Elles se résolvent comme si c'était un système de deux équations avec les deux équations x et y.
Les valeurs trouvées de x et y remplacées en (1) permettront de trouver la valeur de la troisième inconnue z.

2. Méthode de comparaison : on peut résoudre (1), (2) et (3) toutes par rapport à z. En égalisant les valeurs de z dérivant de (2) et (3) à celle dérivant de (1), on obtient deux équations avec les inconnues x et y.
On continue comme pour la deuxième partie du point 1.

3. Méthode de réduction : on multiplie (1) par C₁ et (2) par -C. En ajoutant membre à membre (1) et (2) on obtient une équation avec les inconnues x et y.
On multiplie (1) par C₂ et (3) par -C. En ajoutant membre à membre (1) et (3) on obtient une seconde équation avec x et y.
On continue comme pour la deuxième partie du point 1.

4. Formule de Cramer :
En mettant :

| A B C | = | A1 B1 C1 |   | A2 B2 C2 |	| D B C | x = | D1 B1 C1 |   | D2 B2 C2 |
| A D C | y = | A1 D1 C1 |   | A2 D2 C2 |	| A B D | z = | A1 B1 D1 |   | A2 B2 D2 |

Dans les systèmes de plus de trois équations et autant d'inconnues on utilise la formule de Cramer, ou bien les méthodes de substitution, comparaison et réduction plusieurs fois jusqu'à arriver à deux équations avec deux inconnue.
Une fois déterminée la valeur des deux inconnues, on continue par substitution.