
Extraction manuelle de racine
Les carrés parfaits de 1 à 100 sont les carrés des 9 premiers nombres.
Nombres: 1 2 3 4 5 6 7 8 9
Carrés: 1 4 9 16 25 36 49 64 81
Règle
Pour extraire la racine carrée d'un nombre, on partage ce nombre en tranches de deux chiffres à partir de la droite.
On extrait d'abord la racine carrée de la dernière tranche à gauche, ce qui donne le chiffre des plus hautes unités de la racine et un premier reste ;
on abaisse à la droite de ce reste la tranche suivante du nombre, et on divise les dizaines du nombre ainsi formé par le double de la racine déjà trouvée ; ce qui donne, après essai, le deuxième chiffre de la racine et un deuxième reste;
on abaisse à la droite de ce reste la tranche suivante du nombre, et on opère sur le nombre ainsi formé comme sur le nombre précédent; ce qui donne le chiffre suivant de la racine; et, ainsi de suite, on continue jusqu'à ce qu'on ait abaissé la dernière tranche du nombre. Le dernier reste est le reste de la racine.
Racine carrée d'un nombre entier
Pour extraire à 0.1, à 0.01, à 0.001 près, la racine d'un nombre entier on extrait la racine du nombre entier, on place une virgule à la racine et on continue l'opération en abaissant deux zéros sur la droite des restes successifs de la racine jusqu'à ce qu'on ait à la racine le nombre des chiffres décimaux demandés.
Racine carrée d'un nombre décimal
Pour extraire la racine carrée d'un nombre décimal, on extrait d'abord la racine carrée de la partie entière du nombre, on place une virgule à la racine, puis on continue l'opération en abaissant à la droite des restes successifs, par tranche de deux, les chiffres décimaux du nombre, jusqu'à ce qu'on ait à la racine le nombre des chiffres décimaux demandés.
Racine carrée d'une fraction
Pour extraire la racine carrée d'une fraction, on extrait la racine carrée de chacun des termes de cette fraction. Si possible convertir la fraction en décimales, et procéder ensuite comme ci-dessus.
Extraction abrégée de la racine carrée
On calcule d'abord par la méthode ordinaire la moitié plus un du nombre des chiffres de la racine entière ; puis on divise le reste par le double de la racine trouvée suivie d'autant de zéros qu'il reste de chiffres à obtenir. Le quotient entier est le complément de la racine entière.
Exemple : Extraire la racine carrée de 189 225

Pour extraire manuellement la racine carrée d'un nombre "n" :
Partager votre feuille de travail en deux colonnes.
Délimiter la ligne supérieure de la colonne de droite : c'est ici qu'apparaîtra la valeur de la racine : "v".
Dans la colonne de gauche, écrivez le nombre "n" dont vous souhaitez extraire la racine.
Si le nombre de chiffres avant la virgule est impair, s'occuper du premier chiffre. Sinon s'occuper des deux
premiers. La valeur obtenue s'appelle "x". Écrire "x" en dessous de "n".
Trouver un nombre "a" qui, multiplié par lui même s'approche de "x", sans le dépasser.
Soustraire "a x a" à "x" et écrire cette valeur "r" sous "x".
Reporter la valeur de "a" dans la zone supérieure de la colonne de droite : "v".
Ensuite, répéter les opérations suivantes jusqu'à ce que vous estimiez avoir assez de chiffres significatifs.
Multiplier "v" par deux (en ôtant la virgule) et l'écrire dans la colonne de droite.
Abaisser deux chiffres de "n" au bout de "r". S'il n'y en a plus, abaisser deux 0 et ajouter une
virgule à "v".
Trouver un nombre "a" tel que "(v x 10 + a) x a" s'approche de "r", sans le dépasser.
Soustraire "(v x 10 + a) x a" à "r" pour obtenir la nouvelle valeur de "r".
Reporter la nouvelle valeur de "a" dans la zone supérieure de la colonne de droite : "v".
Exemple détaillé : Calculer la racine de 2
 |
 |
 |
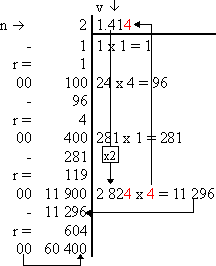 |
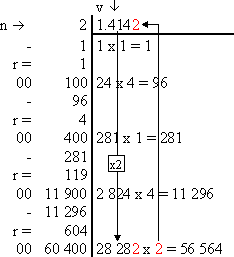 |
Exemple non détaillé : Calcul de la racine de 54.321



La racine cubique de 1 881 365 963 625 = 12345
