x = 60° y= 120°
x = 90° y= 90°
x = 108° y= 72°
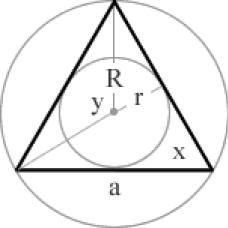
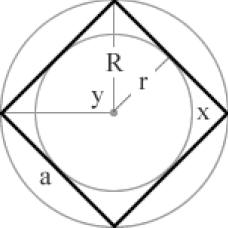
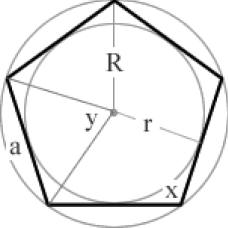
x = 120° y= 60°
x = 128,57° y= 51,43°
x = 135° y= 45°
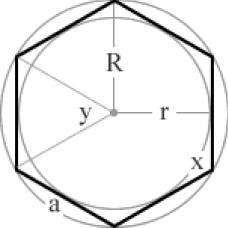
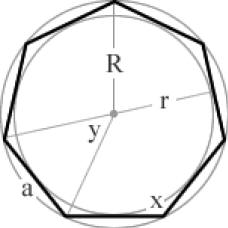
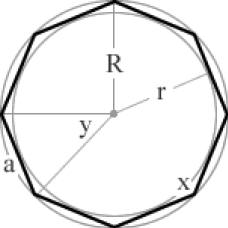
x = 140° y= 40°
x = 144° y= 36°
x = 144,27° y= 32,73°
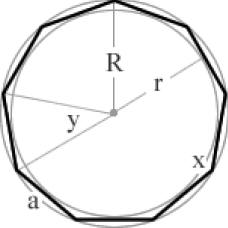
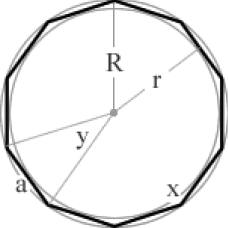
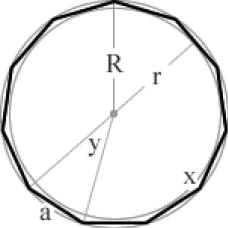
x = 150° y= 30°
x = 152,31° y= 27,69°
x = 154,29° y= 25,71°
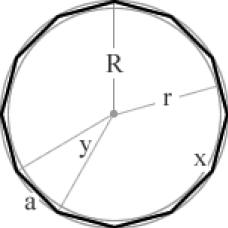
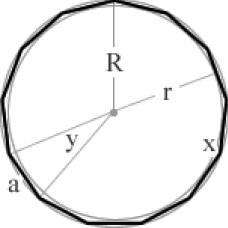
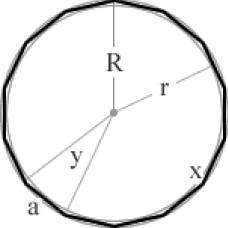
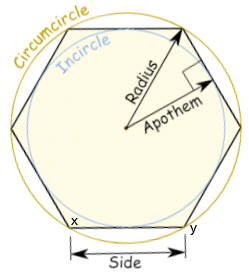
a = 2r tan(π/n)
a = 2R sin(π/n)
P = na
A = (1/4)naČ cot(π/n)
A = nr tan(π/n)
Angles
x + y = 180°
x = (n-2)π / n radians
x = (n-2)/n) x 180° degrees
x = 180 - y
y = (2π / n) radians
y = (360° / n) degrees
y = 180 - x
r = (1/2)a cot(π/n)
r = R cos(π/n)
R = (1/2) a csc(π/n)
R = r sec(π/n)
