Additionneur décimal
Additionneur BCD (décimal codé binaire)
BCD est Binary Coded Decimal, où chaque chiffre décimal (0 à 9) est représenté à l’aide de 4 bits.
Ceci est illustré dans l’exemple ci-dessous:
Exemple : Supposons que nous
ayons le nombre décimal 24, c'est-à-dire (24)10, alors il est
représenté en BCD comme suit :
| 2 | 4 |
| 0010 | 0100 |
De même, (91)10= (1001 0001)2 Et (0011 1001)2 = (39)10
Puisque nous utilisons 4 bits, le nombre représenté peut être compris entre 0000 et 1111, mais en BCD, les nombres 1010, 1011, 1101, 1110 et 1111 sont invalides (non utilisés).
En effet, BCD représente des nombres décimaux et le nombre décimal comporte des chiffres de 0 à 9.
Un additionneur BCD est un circuit combinatoire qui additionne deux nombres BCD et génère une somme également sous forme BCD.
Il existe quelques règles pour l'ajout de BCD (l'ajout de BCD a été discuté en détail dans la section Système de numérotation). Les règles sont :
i. Convertissez les nombres décimaux donnés (à ajouter) sous forme BCD (comme indiqué dans l'exemple). Ajoutez maintenant les bits correspondants de deux nombres dans un groupe de 4 bits (BCD), en commençant par LSB.
ii. Si chacune des sommes de 4 bits est inférieure ou égale à 9, la somme est correcte et est sous forme BCD.
iii. Si l'une des sommes de 4 bits est supérieure à 9 ou si elle génère un report à partir d'une somme de 4 bits, alors la somme n'est pas valide.
Ajoutez (6)10 = (0110)2 à ce groupe invalide et le report résultant est ajouté au groupe BCD d'ordre supérieur suivant:
(6)10= (0110)2 est ajouté pour ignorer 6 numéros BCD illégaux de (1010)2 à ( 1111)2.
Prenons quelques exemples pour comprendre les règles ci-dessus.
Exemple : Additionnez (21)10 à (33)10.
Solution:
| Code BCD | ||
| (21)10 | 0010 | 0001 |
| + | + | + |
| (33)10 | 0011 | 0011 |
| = | = | = |
| (54)10 | 0101 | 0100 |
Puisqu'aucune retenue n'est générée et que les deux sommes de 4 bits sont inférieures à 9, il s'agit donc d'une somme valide.
Exemple: Additionnez (8)10 à (4)10.
Solution:
| Code BCD | |
| (8)10 | 1000 |
| + | + |
| (4)10 | 0100 |
| = | = |
| (12)10 | 1100 |
Aucune retenue n'est générée mais les deux sommes de 4 bits sont supérieures à 9, c'est donc une somme invalide.
Ajoutez 0110 à la somme pour ignorer 6 états invalides et rendre la somme valide.
| Code BCD | ||
| (12)10 | 1100 | |
| + | + | |
| (6)10 | 0110 | |
| = | = | |
| (12)10 | 0001 | 0010 |
Exemple: Additionnez (79)10 à (18)10.
| Code BCD | |||
| 0001 | <-1 | ||
| (79)10 | 0111 | ^ | 1001 |
| + | + | ^ | + |
| (18)10 | 0001 | ^ | 1000 |
| = | = | ^ | = |
| ^ | |||
| (97)10 | 1001 | ^1 | 0001 |
Les deux sommes de 4 bits (1001 et 0001) sont inférieures à 9, mais un report est généré et transmis au groupe BCD suivant, la somme n'est donc pas valide.
Ajoutez 0110 à la somme de 4 bits qui a généré le report afin de rendre la somme valide.
| Code BCD | ||
| 1001 | 0001 | |
| + | ||
| (6)10 | 0110 | |
| = | = | |
| (97)10 | 1001 | 0111 |
Exemple : Additionnez (9)10 à (7)10.
Solution:
| Code BCD | ||
| (9)10 | 1001 | |
| + | + | |
| (7)10 | 0111 | |
| = | = | |
| (16)10 | 1 | 0000 |
| Carry | ||
Ajoutez 0110 à une somme de 4 bits car un report est généré.
| 0000 | |
| + | |
| 0110 | |
| Carry | = |
| 0001 | 0110 |
De la discussion et des exemples ci-dessus, il est conclu que le circuit additionneur BCD pour ajouter deux nombres BCD nécessite :
i. Un additionneur 4 bits.
ii. Un circuit logique pour déterminer si la somme > 9.
iii. Un additionneur 4 bits pour ajouter 0110 à une somme de 4 bits si la somme de 4 bits est supérieure à 9 ou si la retenue est générée par une somme de 4 bits.
Soit les deux nombres BCD A et B où, A = A3 A2 A1 A0 (Augend en BCD)
B = B3 B2 B1 B0 (Addend en BCD)
SOMME = S3S2S1S0 (Somme en BCD)
Maintenant, si la somme est supérieure à 9 S3S2S1S0 est l'un des éléments suivants, ce sont des codes BCD invalides :
| S3 | S2 | S1 | S0 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
La table de vérité complète pour les bits de somme S3S2S1S0 est présentée dans le tableau ci-dessous.
La sortie Y est « 0 » pour une somme de 4 bits valide (0000 à 1001) et Y= « 1 » pour une somme de 4 bits invalide (1010 à 1111).
Table de vérité pour les bits de somme S3S2S1S0
| Entrées | Sorties | |||
| S3 | S2 | S1 | S0 | Y |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
La tableau ci-dessous montre la K-Map pour la sortie Y.
| S1S0 | |||||
| 00 | 01 | 11 | 10 | ||
| S3S2 | 00 | ||||
| 01 | |||||
| 11 | 1 | 1 | 1 | 1 | |
| 10 | 1 | 1 | 1 | ||
D'après le tableau Y = S3S2+ S3 S1
Chaque fois que Y = 1, cela signifie que la somme est supérieure à 9.
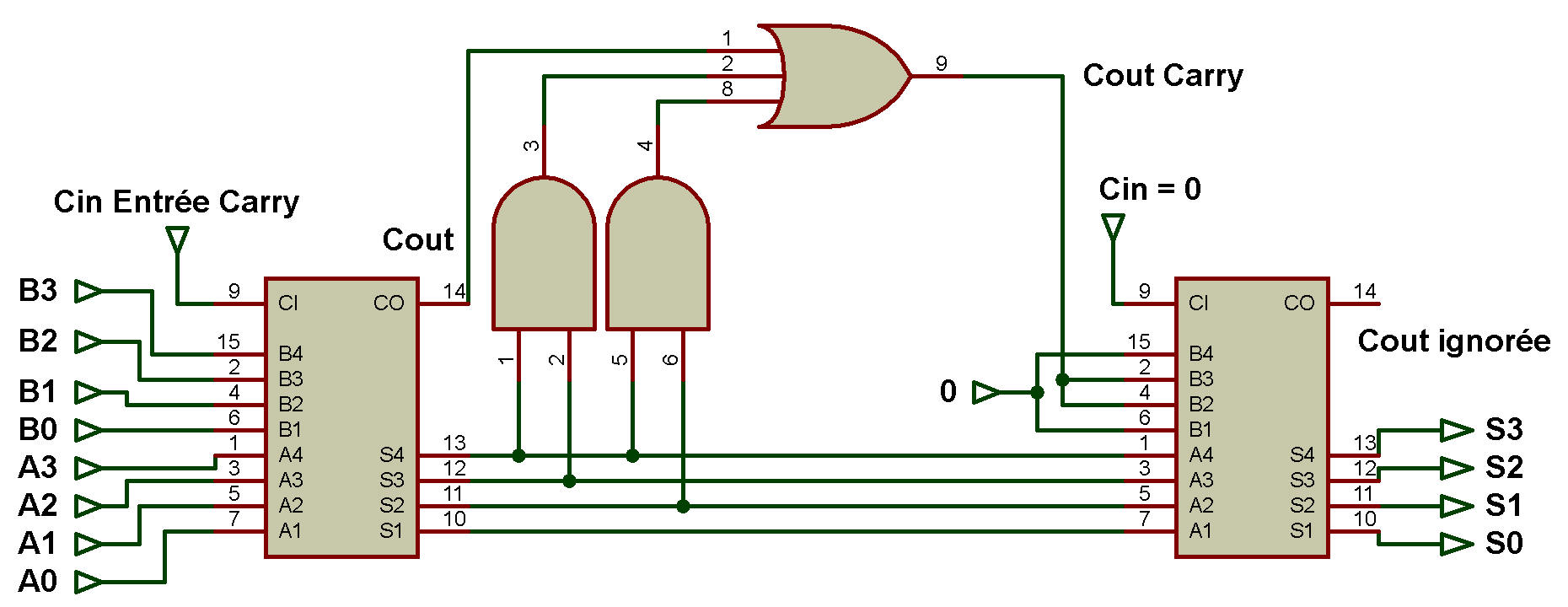
Le schéma fonctionnel de BCD Adder est présenté dans la figure ci-dessous:

Comme le montre la figure, les bits Augend et Addend sont ajoutés à l'aide de l'additionneur binaire complet 1 de 4 bits.
Si la somme de 4 bits (c'est-à-dire S3S2S1S0) est inférieure ou égale à 9 et transporte la sortie Cout à partir de l'additionneur complet binaire 4 bits 1 est égal à « 0 », alors rien (zéro) n'est ajouté à la somme car la somme est valide et est sous forme BCD.
Si la somme de 4 bits (c'est-à-dire S3S2S1S0) est supérieure à 9 ou si la sortie Cout de l'additionneur binaire complet 1 de 4 bits est égale à « 1 », alors 0110 est ajouté à la somme en utilisant l'additionneur 2 binaire de 4 bits.
Si une retenue est générée par cet additionneur binaire complet de 4 bits, alors cette retenue est ignorée.
La somme est désormais valide et se présente sous forme BCD.
