Conception logique numérique

Un compteur est un appareil dont l'architecture est similaire à celle d'un registre.

Le registre de type compteur se compose également d'un groupe de bascules en cascade. Les registres servent uniquement à stocker des données binaires, le compteur sert à compter le nombre d'impulsions appliquées à son entrée d'horloge.

Les compteurs peuvent également compter l'intervalle de temps entre deux impulsions d'horloge ou peuvent également compter la fréquence d'un signal donné.

Le compteur peut être largement classé en compteurs synchrones, compteurs asynchrones ou ondulés et compteurs MOD.

Compteurs asynchrones ou ondulatoires : dans un compteur asynchrone/ondulatoire, les bascules ne sont pas cadencées simultanément, mais la sortie de chaque bascule en cascade est connectée à l'entrée d'horloge de la bascule d'ordre supérieur suivante.

Ainsi, la sortie de chaque bascule pilote la bascule d'ordre supérieur suivante en série. Ce compteur est aussi appelé compteur série.

Compteurs synchrones : dans le compteur synchrone, toutes les bascules sont cadencées simultanément. Les bascules synchrones sont également appelées compteurs parallèles.

Compteur MOD-n : le compteur MOD-n est également appelé compteur diviseur par n.

Ces compteurs sont définis sur la base du nombre d'états qu'un compteur est capable de compter.

Par exemple, le compteur MOD-10 peut compter 10 états.

De même, le compteur MOD-4 est un compteur diviseur par 4 capable de compter 4 états.

Discutons des différents types de compteurs asynchrones/ondulations, des types de compteurs synchrones et des types de compteurs MOD et autres compteurs un par un.

Voici différents circuits intégrés de conteurs

4026BE	7 segment dysplay decade counter
4510BE	Presettable BCD up/down Counter
4017BE	Decade counter
4520	Double compteur binaire
74HC191	Presettable Binary Up/Down Counter
4029BCN	Presettable Binary/Decade Up/Down Counter
14029BCP	Presettable Binary/Decade Up/Down Counter
74HC193	4-Bit Synchronous Up/Down Counters (Dual Clock With Clear).
74LS469NS	8-Bit Binary Up-Down Counter
74LS 592N	8 Bit binary counters with intput registers
74LS90	Divide-by-12 counter decade counter and 4-Bit binary counter
74LS 92N	Divide-by-12 counter decade counter
74HC393	Double compteur binaire
4020	14-Stage Ripple Carry Binary Counters
4040	12-Stage Ripple Carry Binary Counters
74HC4060	14-stages binary ripple counter with oscillator
4060	14-stages binary ripple counter with oscillator
4521	24-stages frequency divider

Compteur asynchrone (ondulation)

Compteurs synchrones

Compteur MOD-N

Compteur de registre à décalage

Logique séquentielle asynchrone

Dans tout circuit logique séquentiel, la sortie dépend non seulement de l'entrée actuelle mais également des informations concernant les entrées et sorties passées.

Les informations concernant les entrées et les sorties passées sont appelées commentaires et sont stockées dans un élément de mémoire. En d’autres termes, un circuit logique séquentiel est un circuit combinatoire avec rétroaction.

Les circuits logiques séquentiels synchrones sont un circuit cadencé car ils ont une horloge qui régule le mécanisme de rétroaction avec un cycle d'horloge approprié.

Dans le circuit logique synchrone, les bascules sont utilisées comme élément de mémoire pour fournir une rétroaction et ces bascules sont pilotées par une horloge.

Ainsi, le circuit logique séquentiel synchrone fonctionne avec un cycle d'horloge. Cela signifie que le circuit génère une sortie uniquement sur le front positif ou négatif de l'impulsion d'horloge.

Les circuits séquentiels asynchrones sont les circuits dont le fonctionnement n'est pas contrôlé par une horloge. Cela signifie que le fonctionnement d'un circuit séquentiel asynchrone dépend du changement du signal d'entrée et que ce changement de signal peut se produire à tout instant. Au fur et à mesure que l'entrée sur la ligne d'entrée change, le circuit séquentiel asynchrone change d'état et génère la sortie requise. L'élément de mémoire dans un circuit logique asynchrone est soit des bascules non cadencées, soit des éléments à retardement. Les circuits séquentiels asynchrones sont utilisés pour concevoir des systèmes numériques qui doivent fonctionner rapidement sans dépendre d'une impulsion d'horloge pour leur fonctionnement.

La figure ci-dessous montre le schéma fonctionnel d'un circuit logique séquentiel asynchrone.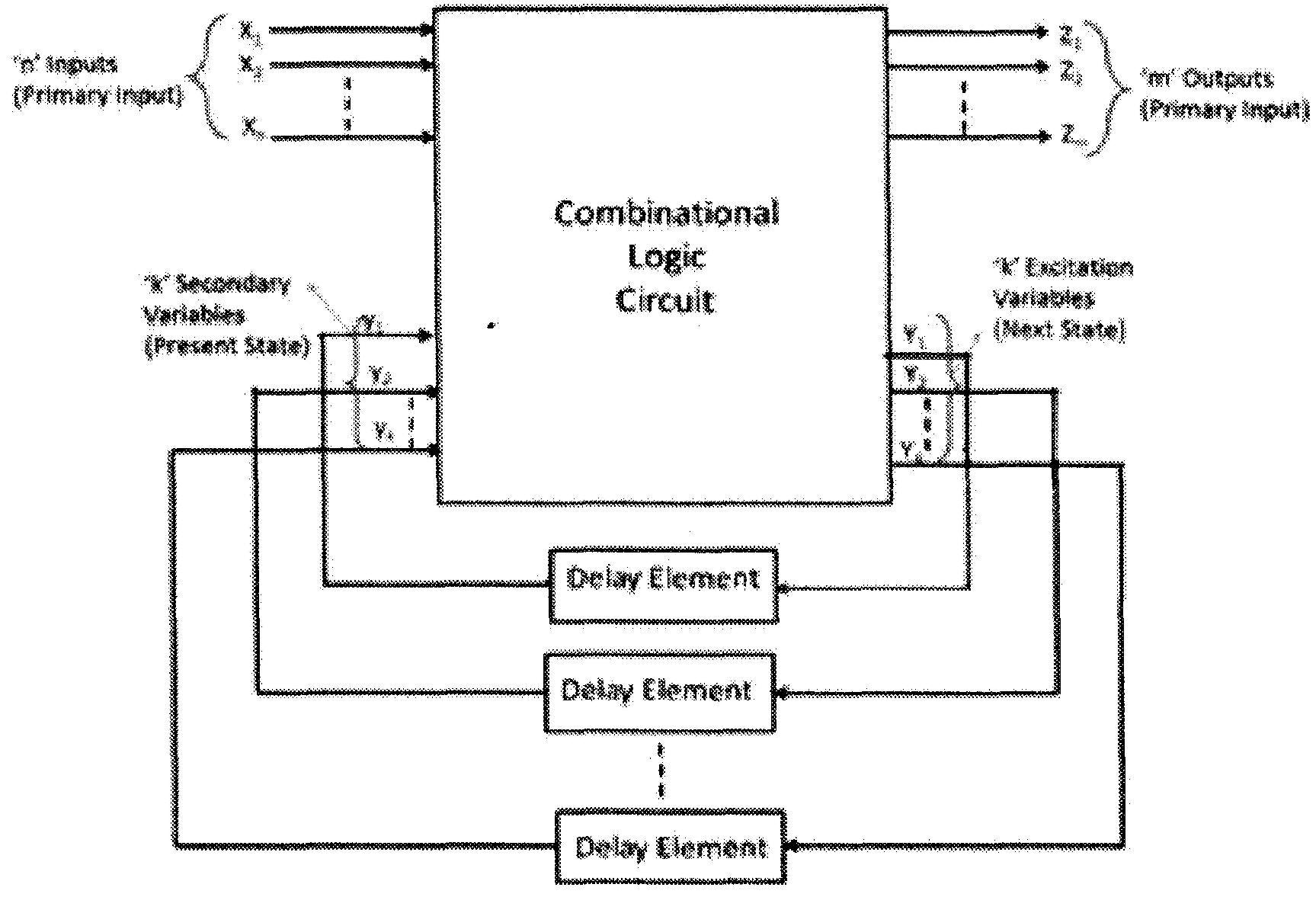

Comme le montre le schéma fonctionnel, les variables secondaires sont les variables de l'état présent et les variables d'excitation sont les variables de l'état suivant dans les circuits séquentiels asynchrones. Lorsque l’une des entrées primaires n est appliquée à la ligne d’entrée, elle passe par le circuit combinatoire.

Cela fait apparaître la nouvelle valeur sur la variable d'excitation « Y ». Ces valeurs passant par l'élément de retard atteignent l'entrée « y » pour devenir la nouvelle entrée de l'état présent. Après cela, sur la base des valeurs d'entrée primaires et secondaires, la sortie « Z » est générée.

Procédure d'analyse

Condition de concurrence

Circuit avec Latch

Procédure de conception

Réduction des tables d'état et de flux

Affectation d'État sans concurrence

Les Dangers

Logique séquentielle asynchrone

Conception logique numérique

Recherche personnalisée