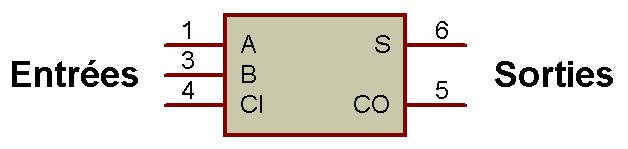
Additionneurs - Soustracteur
Additionneurs
Les additionneurs sont les circuits combinatoires qui effectuent l’addition de nombres binaires. Les additionneurs peuvent être - un demi-additionneur et un additionneur complet. Discutons à la fois du demi-additionneur et de l'additionneur complet un par un.
Demi-additionneur
Le demi-additionneur est un circuit combinatoire qui effectue l’addition de deux bits. Le premier bit est un bit Augend et l’autre bit est un bit Addend. La sortie est une somme et un report (si la sortie d'addition est générée).
Ainsi le demi-additionneur a 2 entrées et 2 sorties. La table de vérité pour le demi-additionneur est présentée dans le tableau ci-dessous:
| Table de vérité du demi-additionneur | |||
| A | B | S (Somme) | C (carry) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Les 2 entrées reçoivent les lettres A et B et les sorties reçoivent les lettres S (Somme) et C (Carry).
Avec deux entrées, il existe 22 = 4 combinaisons de sorties possibles, comme indiqué dans le tableau.
D'après le tableau, il ressort clairement que la sortie « S » est « 1 » lorsque l'entrée « A » est « 1 » ou que l'entrée « B » est « 1 ». La sortie 'C' est '1' uniquement lorsque les deux entrées 'A' et 'B' sont '1'.
La fonction booléenne pour « S » et « C » peut être obtenue à partir du tableau comme indiqué ci-dessous.
S = A'B + AB'= A XOR B
C = AB
Ou bien, nous pouvons également trouver ci-dessus la fonction booléenne pour « S » et « C à l’aide de K-Map comme indiqué ci-dessous.
S = A'B + AB'=A XOR B, C=AB
| K-Map pour 'S' | K-Map pour 'C' | ||||
| B | |||||
| B' | B | B' | B | ||
| A | A' | 1 | |||
| A | 1 | 1 | |||
Le schéma fonctionnel du
demi-additionneur est illustré à la figure ci-dessous:

Le schéma logique du demi-additionneur peut être conçu de l'une des manières suivantes, comme le montrent les figures ci-dessou:
C'est au choix du concepteur de choisir l'un des schémas logiques pour concevoir un demi-additionneur.
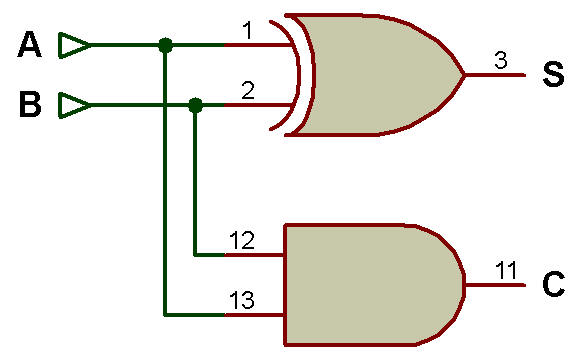
Le schéma logique du demi-additionneur conçu en utilisant la porte XOR et AND
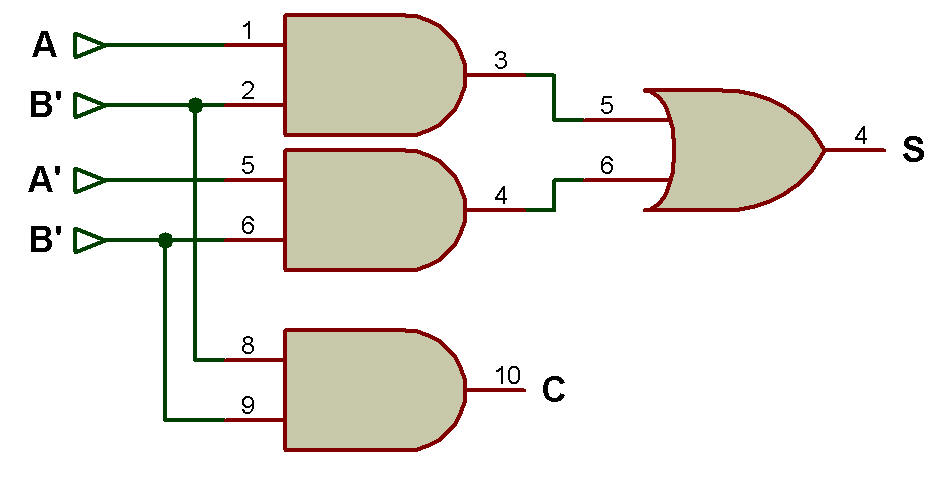
Le schéma logique du demi-additionneur conçu à l'aide des portes AND et OR.
Additionneur complet
L'additionneur complet est un circuit combinatoire qui effectue l'addition de 3 bits : ces 3 bits sont : Augend, Addend et Input carry bit. La sortie générée est la sortie Sum and Carry.
Supposons que nous voulions ajouter deux nombres binaires, où les deux nombres binaires ont 2 ou plus de 2 bits chacun, alors les LSB (bits les moins significatifs) peuvent être ajoutés à l'aide du demi-additionneur (Half Adder) (car il n'y a pas d'entrée de retenue et il n'y a que 2 bits qui il faut l'ajouter).
Maintenant, si le report est généré à partir de cet ajout de LSB, alors ce report est reporté à la colonne immédiatement supérieure.
Cette colonne est maintenant ajoutée à l'aide de l'additionneur complet (augend, addend et report de la colonne précédente).
De même, d'autres bits de colonne supérieurs augend, addend et carry de la colonne précédente sont ajoutés de la même manière à l'aide d'un additionneur complet.
Supposons que si un ajout de colonne ne génère aucun report, alors « 0 » en tant que report est transféré à la colonne immédiatement supérieure et peut être ajouté à l'aide d'un additionneur complet ou même d'un demi-additionneur (car le report est « 0 »).
Notez que chaque bit de colonne (addend, augend et carry) est ajouté à l'aide d'additionneurs complets distincts.
L'exemple ci-dessous montre l'addition à l'aide d'un additionneur complet.
Exemple Additionnez (0111)2 et (1111)2.
Solution:
| Col3 | Col2 | Col1 | Col0 (LSB) | |||
| Entrées Carry | 1 | 1 | 1 | |||
| augend | 0 | 1 | 1 | 1 | ||
| addend | 1 | 1 | 1 | 1 | ||
| 1 | 0 | 1 | 1 | 0 | ||
| Sortie Carry | Somme | |||||
La table de vérité pour l'additionneur complet est présentée dans le tableau ci-dessous:
Table de vérité de l'additionneur complet
| Entrées | Sorties | |||
| X | Y | Z(carry) | S(Somme) | C (Sortie Carry) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Dans le tableau, « X » et « Y » sont des entrées binaires et « Z » est la retenue d'entrée.
'S' est la somme et 'C est le report de sortie.
Avec trois entrées, il existe 23 = 8 combinaisons de sorties possibles, comme indiqué dans le tableau.
D'après le tableau il est clair que la sortie « S » est « 1 », lorsque l'une des variables d'entrée X, Y ou Z est « 1 » ou que les trois variables X, Y et Z sont « 1 ».
La sortie « C » est « 1 » lorsque deux variables d'entrée ou plus sont « 1 ».
La fonction booléenne pour 'S' peut être obtenue à partir de K-Map comme le montre la figure ci-dessous:
| K-Map pour 'S' | |||||
| YZ | |||||
| Y'Z' | Y'Z | YZ | YZ' | ||
| X | X' | 1 | 1 | ||
| X | 1 | 1 | |||
La fonction booléenne pour 'C' peut être obtenue à partir de K-Map comme le montre la figure ci-dessous:
| K-Map pour 'C' | |||||
| YZ | |||||
| Y'Z' | Y'Z | YZ | YZ' | ||
| X | X' | 1 | |||
| X | 1 | 1 | 1 | ||
La fonction booléenne pour S est : S = X'YZ + XYZ' + XY'Z' + XYZ
En simplifiant cette fonction booléenne, S = X'Y'Z + X'YZ' + XY'Z' + XYZ
En organisant les termes que nous obtenons, = X'Y'Z + XYZ + X'YZ' + XY'Z'
= Z (X'Y' + XY ) + Z' (X'Y + XY')
= Z ( X + Y)' + Z' (X + Y) [car a'b + ab' = a + b et (a'b + ab')' = (a + b)' ]
Soit X + Y = A, et (X + Y)' = A', donc
= ZA' + Z'A= Z + A En remplaçant les valeurs de A, nous obtenons,
= Z + (X + Y)
Par conséquent, S = Z + (X + Y) = X + Y + Z
La fonction booléenne pour C est :
C = XZ + YZ + XY
En simplifiant cette fonction booléenne, C = XZ + YZ + XY
= XY + XZ (Y + Y) + YZ (X + X')
= XY + XYZ + XYZ + XYZ + X'YZ
= XY + XYZ + XYZ + X'YZ [Parce que a+a =a]
= XY ( 1 + Z) + Z(XY' + X'Y)
Par conséquent, C = XY + Z (X + Y) [Parce que 1 + Z = Z et XY' + X'Y = X + Y]
Le schéma fonctionnel de l'additionneur complet est présenté dans la ci-dessous:

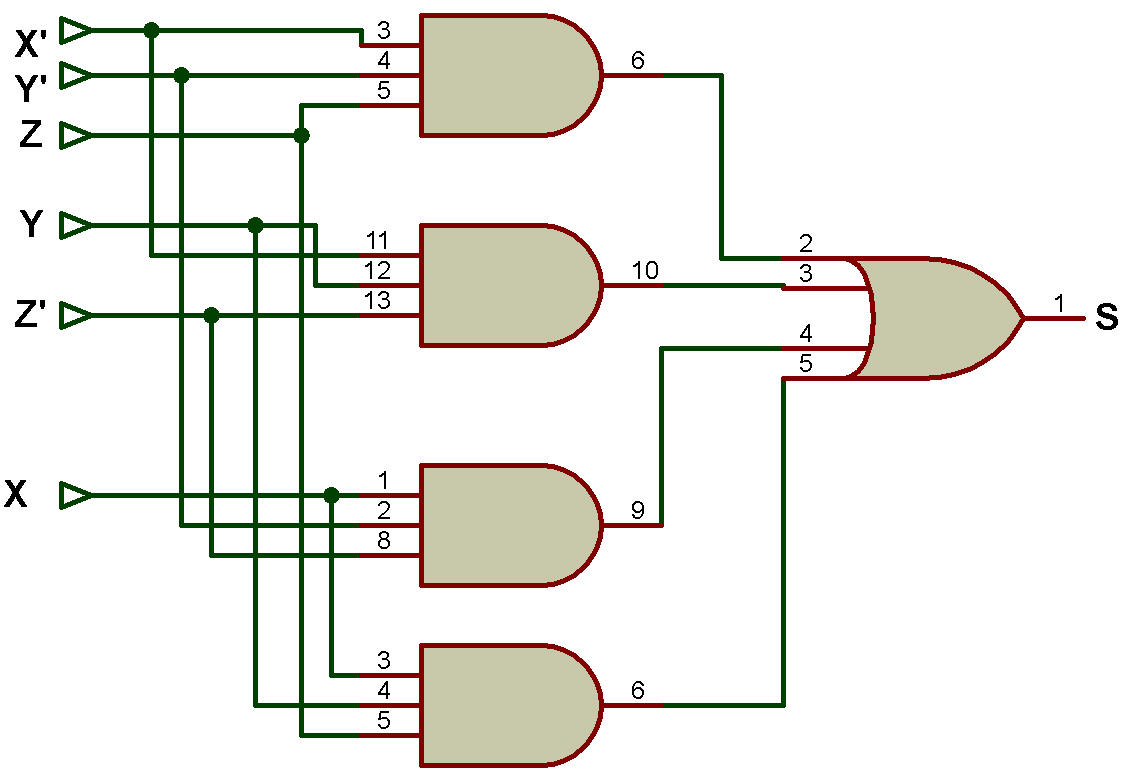
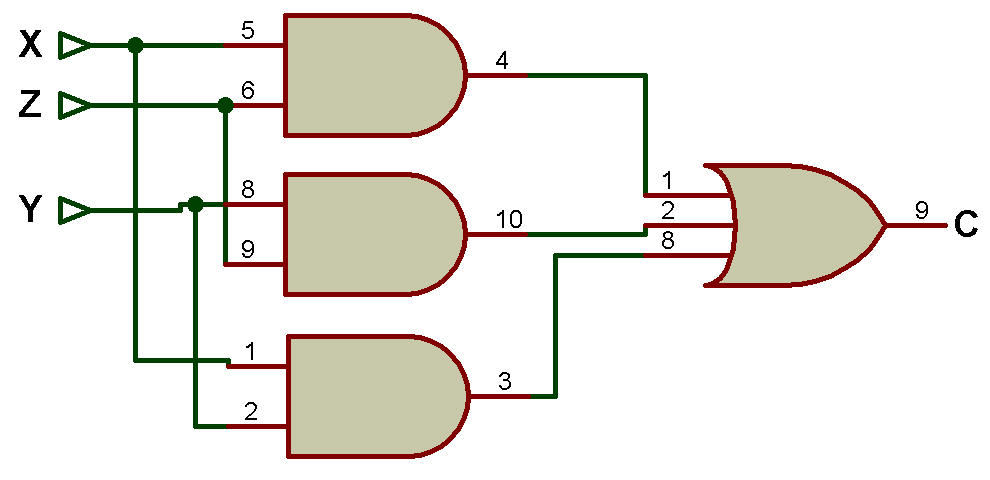
Le schéma logique de l'additionneur complet utilisant la porte AND et OR pour la somme (S) et le report (C) est illustré à la figure ci-dessous:
Schéma logique de l'additionneur complet utilisant la porte ET et OU pour la somme (S) et le report (C)
Le schéma fonctionnel de l'additionneur complet utilisant deux demi-additionneurs et une porte OR est illustré à la figure 2ci-dessous:

Soustracteur
Le soustracteur est le circuit combinatoire qui effectue la soustraction de deux nombres binaires. La soustraction de nombres binaires peut être effectuée de deux manières :
La première méthode est la méthode du complément, dans laquelle le complément du sous-trahend est pris et ajouté au menuend.
Notez que, dans la soustraction 50 -20 = 30, 50 est la minuend, 20 est la subtrahend et 30 est le résultat.
La soustraction par la méthode du complément d'entrée est en fait réalisée à l'aide de l'addition et l'addition peut être mise en œuvre à l'aide d'un additionneur complet.
Cela aboutit à l’utilisation d’un additionneur complet pour l’addition et la soustraction. Ainsi, il est possible de réutiliser les circuits logiques tout en économisant du temps et des coûts.
La deuxième méthode est la même méthode de soustraction traditionnelle que la nôtre, soustraire subtrahend de minuend bit à bit.
Si, dans tous les cas, le bit de minuend est plus petit que son bit du bit subtrahend correspondant, alors l'emprunt de « 1 » est prélevé sur le bit significatif suivant.
Lors de la conception de circuits pour un demi-soustracteur, ces informations sur l'emprunt effectué sont transmises au bit significatif suivant au moyen de la sortie de l'étage actuel passant à l'entrée de cet étage immédiatement supérieur.
Le soustracteur est de deux types :
Demi-soustracteur
Le demi-soustracteur est un circuit combinatoire qui effectue une soustraction de 2 bits.
Le premier bit est le minuend et l'autre est le subtrahend.
La sortie générée est la différence, où Différence = Minuend - Subtrahend.
Il existe également une ou plusieurs sorties « Emprunter » pour spécifier si l'emprunt de « 1 » est effectué ou non.
Ainsi le demi-soustracteur possède 2 entrées et 2 sorties. La table de vérité pour le demi-soustracteur est présentée dans le tableau ci-dessous:
Table de vérité pour le demi-soustracteur
| Entrées | Sorties | ||
| M | S | D (Diff) | B (Emprunt) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Dans le tableau, les 2 entrées reçoivent les lettres M (Minuend) et S (Soustracteur) et les deux sorties reçoivent les lettres D (Différence) et B (Emprunter).
Avec deux entrées, il existe 22= 4 combinaisons de sorties possibles, comme indiqué dans le tableau 2.4.
D'après le tableau, il est clair que l'emprunt 'B' est '1' uniquement lorsque la variable d'entrée M < S (voir la ligne 2 du tableau, c'est-à-dire M=0 et S = 1. Dans ce cas, un emprunt de '1' est à prendre).
Pour tous les autres cas où M>S, B='0'.
La variable de sortie 'D' est '1' uniquement lorsque 'M' n'est pas égal à 'S'
La fonction booléenne pour « D » peut être obtenue à partir de K-Map comme le montre la figure ci-dessous:
D'après K-Map, D = M'S + MS' = MS
| K-Map pour 'D' | |||
| S | |||
| S' | S | ||
| M | M' | 1 | |
| M | 1 | ||
La fonction booléenne pour « B » peut être obtenue à partir de K-Map comme le montre la figure ci-dessous:
| K-Map pour 'B' | |||
| S | |||
| S' | S | ||
| M | M' | 1 | |
| M | |||
De K-Map, B = M'S
Le schéma fonctionnel du demi-soustracteur est présenté à la figure ci-dessous:
Schéma fonctionnel du demi-soustracteur

Diagramme logique du demi-soustracteur conçu à l'aide de la porte XOR, AND et NOT
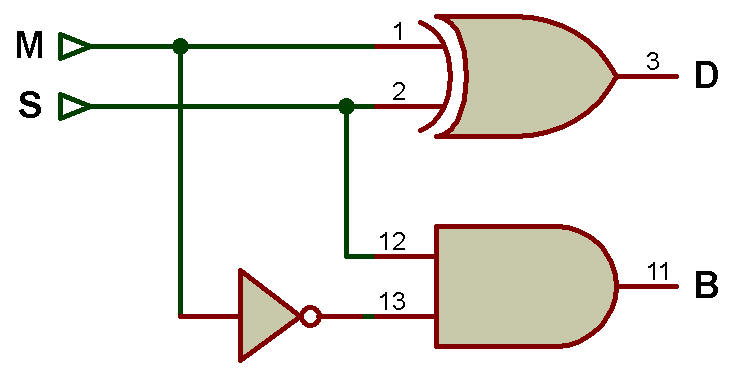
Le schéma logique du demi-soustracteur peut être conçu en utilisant les portes XOR, AND et NOT comme le montre la figure.
Soustracteur complet
Le soustracteur complet est un circuit combinatoire qui effectue une soustraction de 2 bits et veille également à ce que l'emprunt de « 1 » soit effectué par la colonne de sa colonne immédiatement supérieure lors de la soustraction.
Si l'emprunt est effectué, alors les bits de la colonne immédiatement supérieure sont soustraits (minuend-subtrahend) en gardant à l'esprit qu'ils ont emprunté à sa colonne précédente.
Prenons un exemple pour comprendre le soustracteur complet.
Exemple : Effectuez la soustraction (110)2 - (011)2, c'est-à-dire (6)10- (3 )10- = ( 3)10-.
Solution:
| Col2 | Col1 | Col0 (LSB) | |||
| Emprunt | 1 | 1 | |||
| minuend | 1 | 1 | 0 | ||
| subtrahend | 0 | 1 | 1 | ||
| Diff | |||||
Ainsi le soustracteur complet dispose de 3 entrées et 2 sorties.
La table de vérité pour le soustracteur complet est présentée dans le tableau ci-dessous:
| Table de vérité du soustracteur complet | ||||
| Entrées | Sorties | |||
| M | S | Bin | D | Bout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Dans le tableau, les entrées reçoivent les lettres « M » (Minuend), « S » (soustracteur) et « B » (emprunt d'entrée).
Les sorties reçoivent les lettres « D » (différence), « B » (emprunt de sortie).
Avec trois entrées, il existe 23 = 8 combinaisons de sorties possibles, comme indiqué dans le tableau.
La sortie D = M - S - Bin et Bout (emprunt de sortie) pour 8 combinaisons possibles est présentée dans le tableau ci-dessous:
| D = M - S - Bin | Bout |
| 0-0-0 | 0 |
| 0-0-1 | 1 |
| 0-1-0 | 1 |
| 0-1-1 | 1 |
| 1-0-0 | 0 |
| 1-0-1 | 0 |
| 1-1-0 | 0 |
| 1-1-1 | 1 |
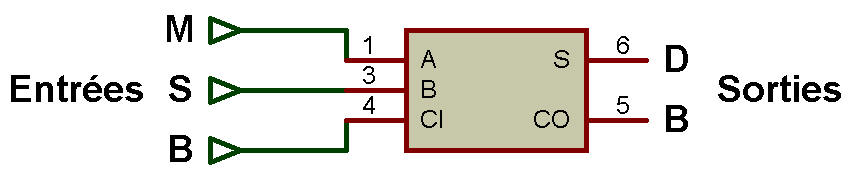
Le schéma fonctionnel du soustracteur complet est présenté en entrée dans la figure ci-dessous:
Schéma fonctionnel du soustracteur complet
La fonction booléenne pour 'D' peut être obtenue à partir de K-Map comme le montre la figure ci-dessous:
| K-Map pour 'Bin' | |||||
| SBin | |||||
| S'Bin' | S'Bin | SBin | SBin' | ||
| M | M' | 1 | 1 | ||
| M | 1 | 1 | |||
De K-Map,
D = M'S'Bin+ M'SBin' +MS'Bin + MSB
La fonction booléenne pour 'Bout' peut être obtenue à partir de K-Map comme le montre la figure ci-dessous:
| K-Map pour 'Bout' | |||||
| SBin | |||||
| S'Bin' | S'Bin | SBin | SBin' | ||
| M | M' | 1 | 1 | 1 | |
| M | 1 | ||||
De K-Map,
Bout = M'Bin + M'S + SBin
La fonction booléenne pour D est : D= M'S'Bin + M'SBin ' +MS'Bin ' + MSB
En simplifiant cette fonction booléenne,
D = M'S'Bin + M'SBin' + MS'Bin' + MSB
= M'(S'Bin + SBin') + M (S'Bin + SB)
= M' (S + Bin) + M ( S + Bin)'
Soit S + B = Yi
Donc, D = M'Y + MY' = M + Y
Maintenant, valeur de remplacement de Y,
D = M + S + Bin
La fonction booléenne de BoutM est :
BoutM = M'Bin + M'S + SBin
En simplifiant cette fonction booléenne,
Bout = M'Bin + M'S+SBin
= M'Bin (S + S') + M'S (Bin+ Bin') + SBin(M +M') -> (On sait que X + X' = 1)
= M'SBin + M'S'Bin + M'SBin + M'S Bin' + MSBin + M'SBin
= M'SBin + M'S'Bin + M'S Bin' + MSBin
—>(M'SBin est apparu 3 fois, donc 2 termes supprimés comme x + x = x )
= M'SBin + M'S Bin'+ M'S'Bin + MSBin
= M'S (Bin +Bin') + Bin(M'S' + MS)
Bout= M'S + Bin(M + S )' -> Parce que x + x' = 1 et x'y' + xy = x + y)
