
Additionneurs - Soustracteur binaire en Parallèle
Un additionneur complet ajoute deux nombres binaires (chaque nombre binaire n'ayant qu'un seul bit) et le bit de report d'entrée.
Ainsi, l'additionneur complet a des entrées - Augend (1 bit), Addend (1 bit) et carry input (1 bit).
Lorsque nous avons des nombres binaires avec plus de 1 bit, supposons 'n' bits , alors nous avons besoin de n' additionneurs complets connectés en parallèle.
Ainsi, un additionneur parallèle binaire est un circuit combinatoire qui a des additionneurs complets connectés en parallèle pour effectuer l'addition de nombres binaires à deux bits.
Un additionneur parallèle binaire accepte les bits d'entrée Augend (An-1, An-2, ...A1, A0) et Addend (Bn-1, Bn-2,...B1, B0) en parallèle et produit des bits de sortie de somme en parallèle.
Le report généré par chaque additionneur complet est connecté à l'entrée de report de l'additionneur d'ordre supérieur suivant.
Les indices n-1, n-2, ...1,0 désignent la position des bits augend et addend (comme n-1 désigne le n-1ème bit, 5 désigne le 5ème bit, 2 désigne le 2ème bit et ainsi de suite d'un nombre binaire).
Un additionneur binaire parallèle à 'n' bits est illustré à la figure ci-dessous:
Schéma fonctionnel de l'additionneur parallèle 'n' Bit

Il convient de noter que les bits de position LSB (bit le moins significatif) peuvent être ajoutés à l'aide d'un demi-additionneur ou d'un additionneur complet avec l'entrée de report de l'additionneur complet définie sur 0, car il n'y a pas de report à la position du bit LSB.
Concevons un additionneur parallèle 4 bits.
La figure ci-dessous montre un additionneur parallèle 4 bits.
Schéma fonctionnel d'un additionneur parallèle 4 bits

Dans un additionneur parallèle de 4 bits, n = 4, signifie que l'augend et l'addend ont chacun 4 bits. L'entrée de report est désignée par Cin.
Comme le montre la figure, l'entrée de report 0 de l'additionneur complet Cin = C-1 où C = 0 car initialement il n'y a pas d'entrée de report.
Dans un additionneur parallèle, le temps nécessaire pour effectuer l'addition est décidé par le retard introduit par le report. Le report se propage (ondulations) à travers des additionneurs complets.
Dans le pire des cas, la retenue du premier étage doit se propager du premier additionneur au dernier additionneur, c'est-à-dire du LSB (bit le moins significatif) au MSB (bit le plus significatif).
En fonction de la génération de report et de la propagation d'un additionneur complet à l'additionneur complet suivant (où les additionneurs complets sont connectés en parallèle), les additionneurs parallèles sont classés en deux types :
i. Carry Propagate Adder (ou Ripple Carry Adder)
ii. Carry-Look Ahead Adder
L'ajout utilisant un additionneur parallèle dont nous venons de parler ci-dessus (dans la section est Ripple Carry Adder).
Comme le montrent les figures, la sortie Sum and Carry to next stage n'est valide qu'après un délai suffisant.
En effet, une somme et un report valides ne peuvent se produire que quelque temps après l'apparition de l'entrée de report de cette étape.
Ainsi, plus le nombre de bits à ajouter est grand, plus le temps nécessaire à son ajout est important. Un tel additionneur parallèle est appelé Ripple Carry Adder.
Supposons que nous souhaitions effectuer l'addition montrée dans l'exemple 4 en utilisant Ripple Carry Adder.
Exemple: (0101)2 + (0011)2, tels que les bits augend sont A3 A2 A1 A0 = 0101
et les bits addend sont B3 B2 B1 B0 = 0011
Solution : ceci est illustré à la figure ci-dessous:
| Col3 | Col2 | Col1 | Col0 (LSB) | |
| Entrées Carry | 1 | 1 | 1 | |
| augend | 0 | 1 | 0 | 1 |
| addend | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | |
| Sortie Carry | Somme | |||
Pour l’ajout, nous avons besoin d’un additionneur parallèle 4 bits.
Supposons maintenant que chaque additionneur complet nécessite 20 ns (nanosecondes) pour produire la somme et la retenue, alors le délai de propagation est de 20 ns par additionneur complet.
Ainsi, le report final au Full Adder 3, comme le montre la figure ci-dessous, sera produit après un délai de 20 (délai de propagation du Full Adder 0) + 20 (délai de propagation du Full Adder 1) + 20 (délai de propagation du Full Adder 2) = 60 ns.
La Somme S3 finale apparaîtra après 60 ns + 20 ns (délai de propagation du Full Adder 3) = 80 ns.
Ripple Carry Adder

Pour résoudre ce problème de retard de propagation, nous disposons d'un autre type d'additionneur parallèle, à savoir l'additionneur Carry-Look Ahead.
ii Carry-Look Ahead.
Carry-Look Ahead Adders (CLAA) est un additionneur parallèle qui accélère le processus d'addition en réduisant le temps de propagation du report.
Supposons que nous souhaitions ajouter 2 nombres binaires de 4 bits chacun en utilisant un additionneur complet.
On note ces deux nombres par les lettres A et B, on a donc :
| Entrées Carry | C3 | C2 | C1 | C0 |
| augend A= | A3 | A2 | A1 | A0 |
| addend B = | B3 | B2 | B1 | B0 |
| C3 | S3 | S2 | S1 | S0 |
| Sortie Carry | Somme | |||
L'addition ci-dessus est effectuée en sortie à l'aide d'additionneurs complets, ici l'entrée Cin est égale à 0.
Voyons la table de vérité pour l'additionneur complet comme indiqué dans le tableau ci-dessous:
Notez que ce tableau est le même que celui discuté dans le tableau dans la section Additionneurs - Soustracteur sauf que la variable A est utilisée à la place de la variable X, la variable B est utilisée à la place de Y, la variable C est utilisée à la place de Z et la variable C est utilisée à la place de C.
| Entrées | Sorties | ||||
| No. Ligne | A | B | Cin | S(Somme) | Cout |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 | 1 |
| 5 | 1 | 0 | 0 | 1 | 0 |
| 6 | 1 | 0 | 1 | 0 | 1 |
| 7 | 1 | 1 | 0 | 0 | 1 |
| 8 | 1 | 1 | 1 | 1 | 1 |
D'après la table de vérité nous pouvons voir qu'il existe des conditions pour que la sortie de retenue soit « 1 ».
Les lignes 4 et 6 montrent que la sortie de report Cout est « 1 » lorsque A = 1 ou B = 1 et Cin = 1.
Les lignes 7 et 8 montrent que Cout = 1 lorsque A = 1 et B = 1, que ce soit Cin = 1 ou 0.
Ainsi le carry Cout peut se résumer ainsi :
Cout =AB + (AB)Cin
De la fonction booléenne ci-dessus pour Cout , nous pouvons conclure que,
a. Une retenue est générée lorsque les entrées A et B sont toutes deux à « 1 », que Cin = 1 ou 0.
Cin est la retenue générée par l'ajout de colonne précédent et pour l'ajout de LSB, Cin est 0.
C'est ce qu'on appelle la génération de report.
Soit « G » désignant le report et la génération.
Donc G = AB
b. Une retenue est propagée lorsque A = 1 ou B = 1, c'est-à-dire A B = 1 à condition que Cin soit également 1.
C'est ce qu'on appelle la propagation de retenue.
Soit « P » pour la propagation du transport.
Donc,
P = AB
Maintenant Cout = G + PCin
Où Cout est le report généré par l'additionneur complet à une étape donnée.
L'additionneur Carry-Look Ahead utilise ces deux fonctions - carry generate et carry propate pour accélérer le processus d'addition.
Considérons maintenant un additionneur parallèle de 4 bits comme le montre la figure ci-dessous. Nous désignons le report d'entrée vers le premier Full Adder 0 par C-1 et C-1 = 0 car initialement il n'y a pas de report.

Comme le montre la figure, C0 est le report généré par Full Adder 0 après avoir ajouté A0 B0 et C-1, C0 est introduit comme retenue d'entrée dans l'additionneur complet 1.
C1 est la retenue générée par l'additionneur complet 1 après avoir ajouté A1B1 et C0. C1 est introduit comme retenue d'entrée dans l'additionneur complet 2.
C2 est la retenue générée par l'additionneur complet 2 après en ajoutant A2B2 et C1. C2 est envoyé comme report d'entrée à l'additionneur complet 3.
C3 est la sortie de report finale générée par Full Adder 3 après avoir ajouté A3 B3 et C2
Donc,
C0 = G0 + P0 Cin
C0 = G0 + P0C-1
C0= G1 + P1C0
C1 = G1+ P1C0 = G1+P1(G0 +P0C-1)
-> valeur de remplacement de C0 à partir de la fonction ci-dessus
C1 = G1 + P1G0 + P1P0C-1
C2 = G2+ P2C1 = G2+ P2(G1+P1G0 +P1P0C-1)
—> valeur de remplacement de C1 à partir de la fonction ci-dessus
C2 = G2 + P2G1 + P2P1G0 + P2P1P0C-1
C3 = G3+P3C2 = G3+P3(G2+ P2G1+P2P1G0 + P2P1P0C-1)
—> valeur de remplacement de C2 ci-dessus
C3 = G3+P3G2 + P3P2G1+ P3P2P1G0 + P3P2P1P0C-1
Ainsi
Cn = Gn+PnGn-1 + PnPn-1Gn-2 + PnPn-1Pn-2Gn-3 ... + PnPn-1 .. P0C-1
Où 'n' est le nième étage de l'additionneur complet connecté en parallèle.
Ainsi, nous pouvons dire que la sortie de report à n'importe quelle étape dépend uniquement de l'entrée initiale report C-1 de ses fonctions de génération et de propagation de report et de la fonction de génération et de propagation de report des étapes précédentes uniquement.
Comme, C3= G3 + P3 G2 + P3 P2 G1+ P3P2 P1 G0+ P3 P2 P1 P0 C-1
Où, C , est le report d'entrée initial.
G3 et P3 ont leurs fonctions (C3) de génération et de propagation de transport.
G2G1G0P2P1 et P0 (fonctions de génération et de propagation de report de l'étape précédente).
La retenue de sortie pour n'importe quel étage C1C2C3 ... Cn est une fonction booléenne sous forme SOP et peut donc être implémentée à l'aide d'une porte à deux niveaux - soit AND-OR, soit des portes NAND-NAND équivalentes.
La transmission de sortie pour n'importe quel étage nécessitera autant de temps que nécessaire pour que le signal passe à travers 2 portes.
Ainsi, le retard de l'additionneur Carry-Look forward est de deux niveaux de porte.
Deux niveaux de porte -> AND-OR ou NAND-NAND.
Le schéma logique d'un additionneur Carry-Look Ahead est présenté dans la figure ci-dessous:
Schéma logique de l'additionneur Carry-Look Ahead 4 bits
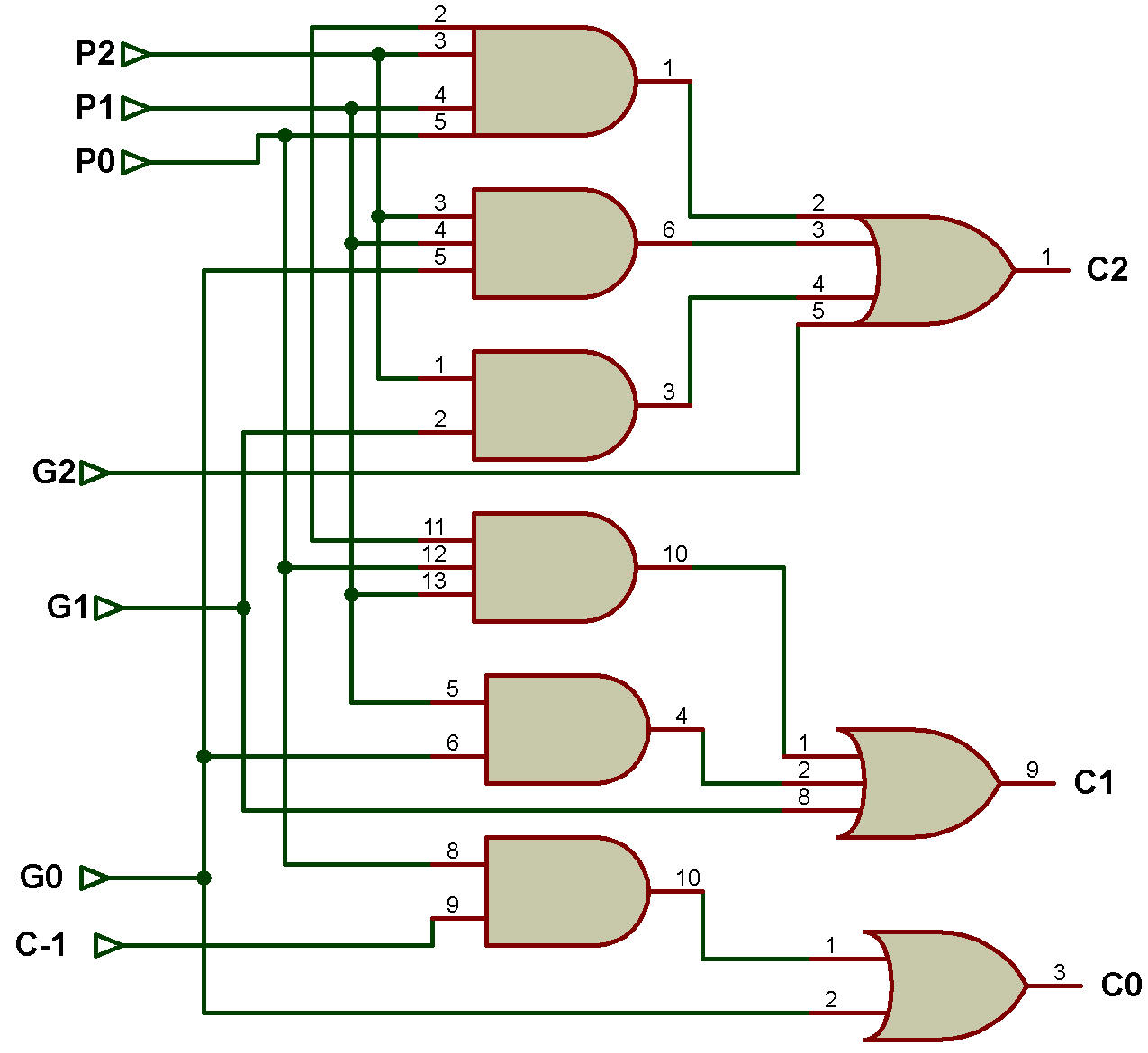
Comme le montre la figure, C est le report d'entrée initial vers Full Adder 0.
C0 = G0 + P0 C-1 et nécessite :
i. Porte AND (2 entrées)
ii. Porte OR (2 entrées)
C1 = G1 + P1G0+ P1P0 C-1 et nécessite :
i. Porte AND (2 entrées)
ii. Porte AND (3 entrées)
iii. Porte OR (3 entrées)
C2 = G2 + P2G1 + P2 P1G0+ P2P1P0C-1 et nécessite :
i. Porte AND (2 entrées)
ii. Porte AND (3 entrées)
iii. Porte AND (4 entrées)
iv. Porte OR (4 entrées)
Le schéma fonctionnel d'un additionneur Carry-Look Ahead est illustré dans la figure ci-dessous:
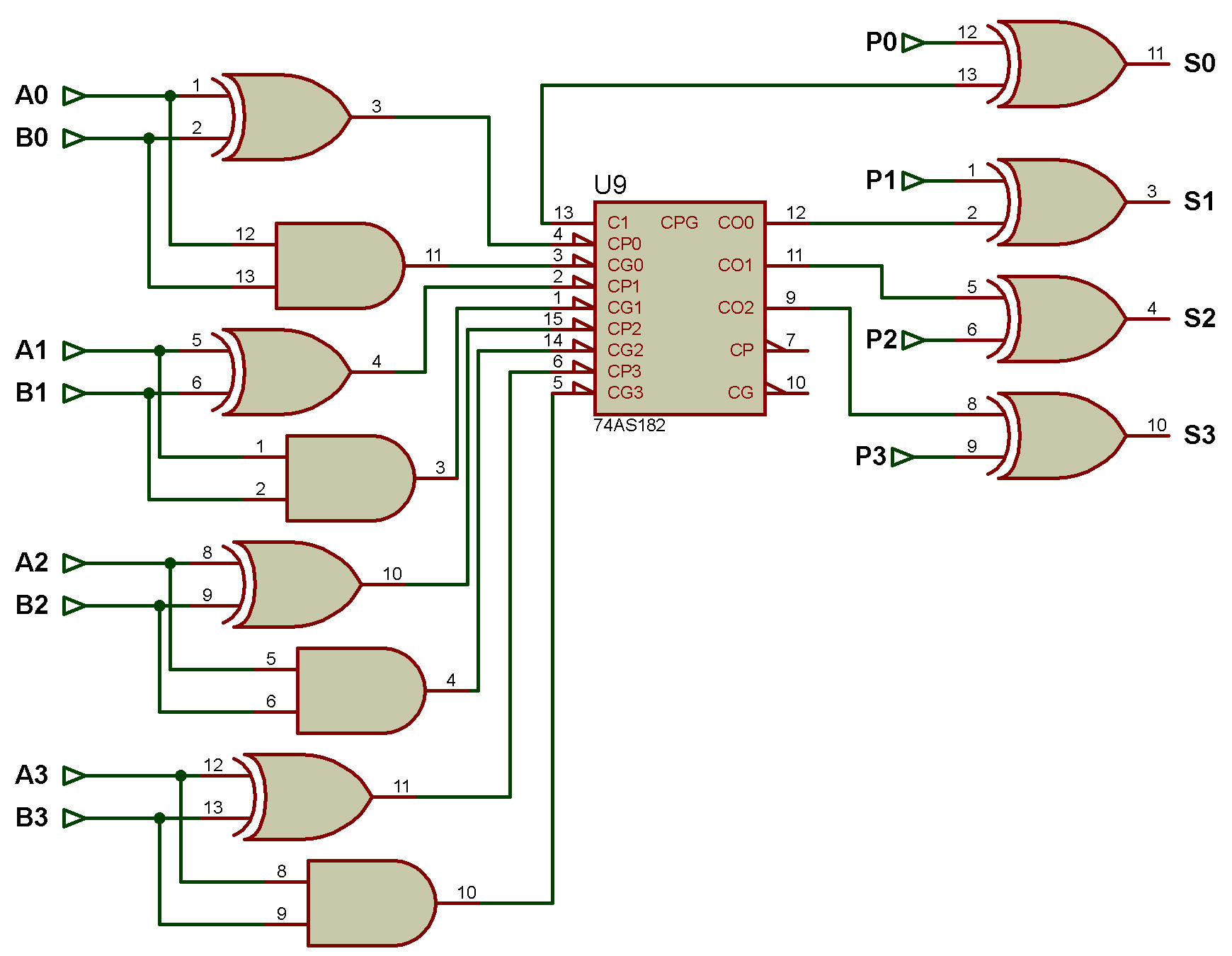
Un additionneur Carry-Look Ahead peut être mis en cascade pour augmenter la taille des mots par multiples de 4 bits.
Par exemple, on peut mettre en cascade 2 additionneurs Carry-Look Ahead pour ajouter deux nombres binaires de 8 bits chacun.
De la même manière, mettez en cascade 4 additionneurs Carry-Look Ahead pour ajouter deux nombres binaires de 16 bits chacun et ainsi de suite.
Soustracteur binaire parallèle
Dans un système numérique, nous savons que la soustraction de deux nombres binaires peut être effectuée plus facilement à l'aide du système complémentaire (les compléments ont déjà été abordés dans la section Système de numérotation).
Dans une méthode de complément, A - B est effectué en prenant le complément à 2 de B et en l'ajoutant à A.
Ainsi, les complexités de la procédure de soustraction normale (soustraction que nous effectuons en mathématiques en soustrayant un nombre de l'autre et en empruntant si nécessaire) sont évitées et les circuits utilisés pour l'addition de deux nombres binaires peuvent également être utilisés avec de légères modifications.
Prenons un exemple.
Exemple : Effectuez A - B en utilisant le complément à 2, où A = 1001 et B = 0110.
Solution : A= 100 et B = 0110
Prendre le complément à 2 de B, B = 0110
Complément à 1 de B = 1001
Complément à 2 de B = 1001 + 1 = 1010
Ajoutez maintenant le complément à 2 de B à A
1001 + 1010 = 1 0011
Ainsi, nous avons vu dans l'exemple que le complément à 2 de B est obtenu en prenant d'abord le complément à 1 et ensuite en ajoutant « 1 » au LSB de B.
Le complément à 1 peut être implémenté à l'aide d'un inverseur, puis « 1 » peut être ajouté au LSB de B en fournissant une retenue d'entrée Cin= 1.
Ceci est illustré dans la figure ci-dessous:
Soustracteur parallèle 4 bits

La figure est un soustracteur parallèle de 4 bits qui utilise quatre additionneurs complets pour effectuer l'addition de A avec le complément à 2 de B.
Ici,
C-1 est l'entrée de report initiale et est égale à 1.
C3 est la sortie de report final.
Les bits de somme sont générés comme :
S0 = A0 + (B0)' + 1
Additionneur-soustracteur parallèle binaire
L'additionneur-soustracteur parallèle binaire, comme son nom l'indique, est un circuit combinatoire qui effectue à la fois l'addition et la soustraction dans un seul circuit.
L'additionneur-soustracteur parallèle binaire à 4 bits est illustré à la figure ci-dessous:
Additionneur-soustracteur parallèle binaire 4 bits
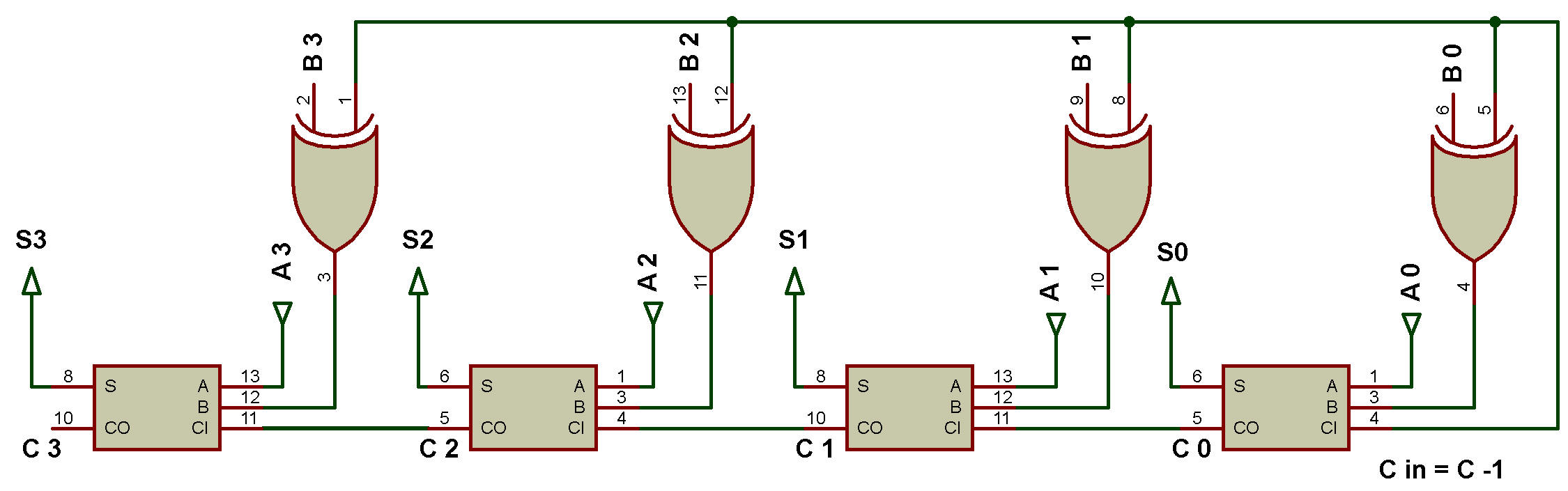
Comme le montre la figure, nous avons quatre additionneurs complets notés - FA0, FA1, FA2, FA3.
Nous avons les entrées A(A0 à A^) et B(B0 à B3).
Les bits d'entrée A (A0 à A3) sont connectés directement aux additionneurs complets FA0 à FA3, respectivement et les bits d'entrée B(B0 à B3) sont connectés via une porte XOR aux additionneurs complets FA0 à FA3, respectivement.
Toutes les 4 portes XOR ont une entrée supplémentaire « M ».
« M » est l'entrée de mode et contrôle le fonctionnement du circuit.
Lorsque M = 0, le circuit se comporte comme un additionneur parallèle 4 bits car la porte XOR reçoit l'entrée B et « 0 ».
Donc, B + 0 = B
L'additionneur complet FA0 reçoit dans ce cas les entrées A0, B0 et Cin = C , = 0.
FA0 effectue donc l'addition :
A0 + B0 + C-1 = A0 + B0 +0 = A0 + B0.
Donc S0 = A0 + B0.
S1 = A1 + B1+ C0
S2 = A2 + B2 + C1
S3 = A3 + B3 + C2
C3 est le report de sortie final.
Lorsque M = 1, le circuit se comporte comme un soustracteur parallèle 4 bits car la porte XOR reçoit l'entrée B et « 1 ».
Donc,
B + 1 = B' [B + 1] = B'1 + 1' B = B' + 0 = B'
L'additionneur complet FA0 reçoit dans ce cas les entrées A0, B0 et Cin = C-1 = M = 1.
FA0 effectue donc une soustraction en utilisant la méthode du complément à 2 :
A0 + (B0)'+C-1= A0 + (B0)' + 1
Donc S0 = A0 + (B0)'+1
S1 = A1 + (B1)' + C0
S2 = A2 + (B2)' + C1
S3= A3 + (B3)' + C2
C3 est le report de sortie final.
