Affectation d'État sans concurrence
Logique séquentielle asynchrone
Dans cette section, nous verrons comment éviter les conditions de concurrence critique dans la table de transition en attribuant correctement des valeurs binaires à l'état.
Cela signifie que pour avoir une table de transition sans concurrence critiques, il est nécessaire que chaque fois qu'il y a une transition (changement) d'état d'un état stable à un autre, une seule variable d'état binaire change à la fois.
Par exemple, supposons que nous ayons l'état a = 00, b = 01 et c = 11, alors la transition (changement) d'état de 'a' (00) à 'b' (01) n'a changé qu'une seule variable, mais la transition (changement) d'état de 'a'(00) à 'c'(11) a modifié deux variables conduisant à une condition de concurrence critique.
Dans la section suivante, nous prendrons des exemples pour expliquer comment les conditions de concurrence critiques peuvent être évitées dans la table de transition.
Le premier exemple pris est d'avoir trois lignes dans la table de flux.
Le deuxième exemple pris est d'avoir quatre lignes dans la table de flux.
La procédure décrite dans ces deux exemples peut ensuite être appliquée à des tables de flux comportant un nombre quelconque de lignes et de colonnes.
Exemple de tableau de flux à trois lignes
Considérons le tableau de flux comme le montre le tableau ci-dessous. Ce tableau de flux est réduit au nombre minimum d'états.
Également dans le tableau de flux, la sortie n'est pas affichée uniquement pour rendre le tableau simple à comprendre.
| x1x2 | ||||
| 00 | 01 | 11 | 10 | |
| a | a | b | c | a |
| b | a | b | b | c |
| c | a | c | c | c |
À partir du tableau de flux de la figure, on peut voir que les transactions d'État suivantes ont eu lieu :
i. De l'état a(00) à l'état b(01) - Voir la première ligne, la deuxième colonne
ii. De l'état a(00) à l'état c(11) - Voir la première ligne, la troisième colonne
iii. De l'état b(01) à l'état a(00) - Voir deuxième ligne, première colonne
iv. De l'état b(01) à l'état c(11) - Voir deuxième ligne, quatrième colonne
v. Indiquez c(11) à l'état a(00) - Voir troisième ligne, première colonne
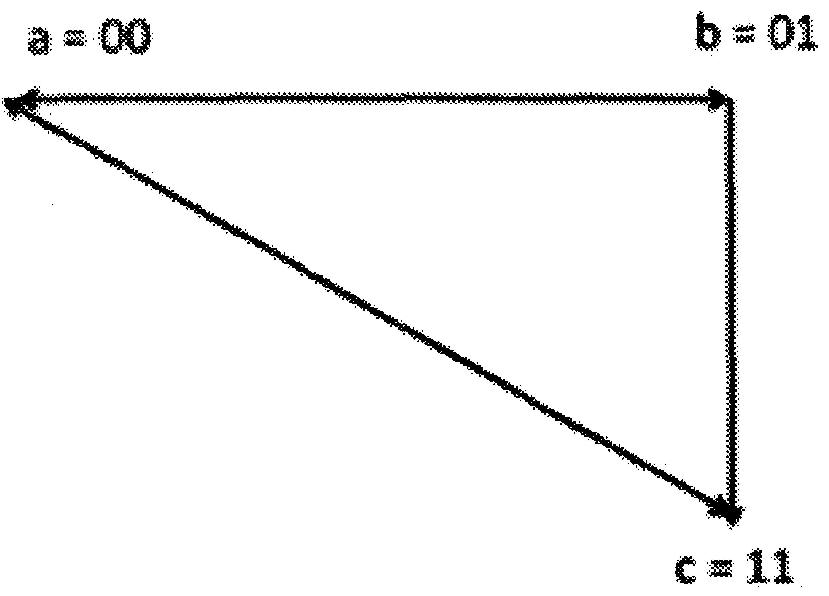
Toutes ces transitions ci-dessus sont représentées dans le diagramme de transition de la figure ci-dessous:

La transition de l'état « a » (00) à l'état « c » (11) et la transition de l'état « c » (11) à l'état « a » (00) montrent une condition de concurrence car deux états binaires sont modifiés en même temps.
Puisque la transition de l'état 'a' à l'état 'c' peut passer par l'état 'b' comme : l'état a (00) à l'état b(01) puis l'état c(11), il s'agit donc d'une condition de concurrence critique.
La transition de l'état « c » à l'état « a » ne passe par aucun autre état donc condition de concurrence non critique.
Pour éviter une situation de concurrence critique et obtenir une affectation sans concurrence, nous ajouterons une quatrième ligne supplémentaire au tableau de flux.
Le tableau de flux ci-haut est modifié en ajoutant une quatrième ligne et en nommant cette quatrième ligne comme « d ».
Ce tableau de flux modifié est présenté ci-dessous:
| x1x2 | ||||
| 00 | 01 | 11 | 10 | |
| a | a | b | d | a |
| b | a | b | b | c |
| c | d | c | c | c |
| d | a | - | c | - |
La quatrième ligne, reçoit la valeur binaire 10, qui est adjacente à la fois à a (00) et à c (11).
Notez que : deux valeurs binaires sont dites adjacentes si elles ne diffèrent que par une seule variable.
Désormais, la transition de l'état « a » à « c » doit maintenant passer par « d ». Cela signifie que les variables binaires passent de a = 00 à d = 10 puis à c = 11, évitant ainsi une concurrence critique.
Ceci est illustré dans le tableau en remplaçant la troisième colonne de la première ligne par d et la troisième colonne de la quatrième ligne par c.
De même, la transition de l'état « c » à « a » doit désormais passer par « d ».
Ceci est illustré dans le tableau en remplaçant la première colonne de la troisième ligne par d et la première colonne de la quatrième ligne par a.
À partir du tableau de flux modifié, on peut voir que les transactions d'état suivantes ont eu lieu :
i. De l'état a(00) à l'état b(01) - Voir la première ligne, la deuxième colonne,
ii. De l'état a(00) à l'état d(10) - Voir la première rangée, la troisième colonne,
iii. De l'état b(01) à l'état a(00) - Voir la deuxième ligne, la première colonne,
iv. De l'état b(01) à l'état c(11) - Voir deuxième rangée, quatrième colonne,
v. De l'état c(11) à l'état d(10) - Voir la troisième rangée, première colonne,
vi. De l'état d(10) à l'état a(00) - Voir la première colonne de la quatrième ligne,
vii. De l'état d(10) à l'état c(11) - Voir la quatrième ligne, la troisième colonne.
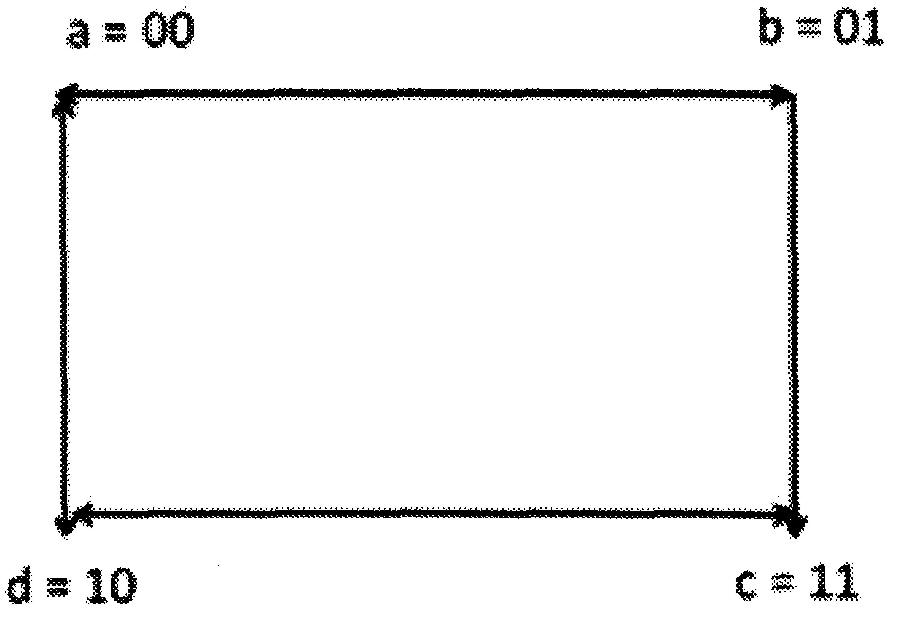
Toutes ces transitions ci-dessus sont représentées dans le diagramme de transition de la figure ci-dessous:
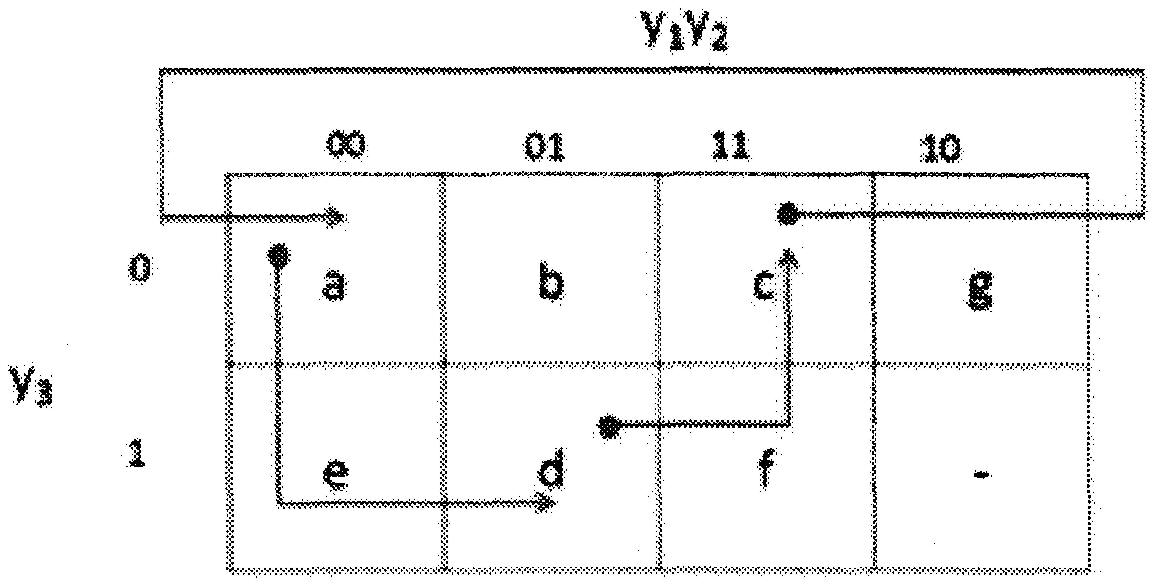
La table de transition pour la table de flux modifiée est illustrée à la figure ci-haut.
Tous les « a » montrés dans le tableau de flux de la figure sont représentés par la valeur binaire 00 dans le tableau de transition, tous les « b » représentés dans le tableau de flux de la figure sont représentés par la valeur binaire 01 dans la transition.
Dans le tableau de transition, tous les « c » indiqués dans le tableau de flux de la figure sont représentés par la valeur binaire 11 dans le tableau de transition et tous les « d » indiqués dans le tableau de flux de la figure sont représentés par la valeur binaire 10 dans le tableau de transition.
Ainsi, à partir de l'exemple ci-dessus, nous avons conclu que l'ajout d'une ligne supplémentaire dans la table de flux peut empêcher une situation de concurrence critique.
Cependant, l'ajout d'une seule ligne supplémentaire peut souvent ne pas suffire à empêcher les concurrence critiques, et il peut être nécessaire d'ajouter deux lignes supplémentaires ou plus dans la table de flux.
Cette possibilité est démontrée dans la section suivante.
Exemple de tableau de flux à quatre lignes
Considérons le tableau de flux comme le montre la figure ci-dessous:
| x1x2 | ||||
| 00 | 01 | 11 | 10 | |
| a = 00 | b | a | d | a |
| b = 01 | b | d | b | a |
| c = 11 | c | a | b | c |
| d = 10 | c | d | d | c |
Ce tableau de flux est réduit au nombre minimum d'états.
Également dans le tableau de flux, la sortie n'est pas affichée uniquement pour rendre le tableau simple à comprendre.
À partir du tableau de flux de la figure, on peut voir que les transactions d'État suivantes ont eu lieu :
i. De l'état a(00) à l'état b(01) - Voir la première ligne, la première colonne,
ii. De l'état a(00) à l'état d(10) - Voir première ligne, troisième colonne.
iii. De l’état b(01) à l’état d(10) – Voir deuxième ligne, deuxième colonne.
iv. De l'état b(01) à l'état a(00) - Voir deuxième rangée, quatrième colonne,
v. De l'état c(11) à l'état a(00) - Voir troisième ligne, deuxième colonne,
vi. De l'état c(11) à l'état b(01) - Voir troisième ligne, troisième colonne,
vii. De l’état d(10) à l’état c(11) – Voir la première colonne de la quatrième rangée.
Toutes ces transitions ci-dessus sont représentées dans le diagramme de transition de la figure ci-dessous:
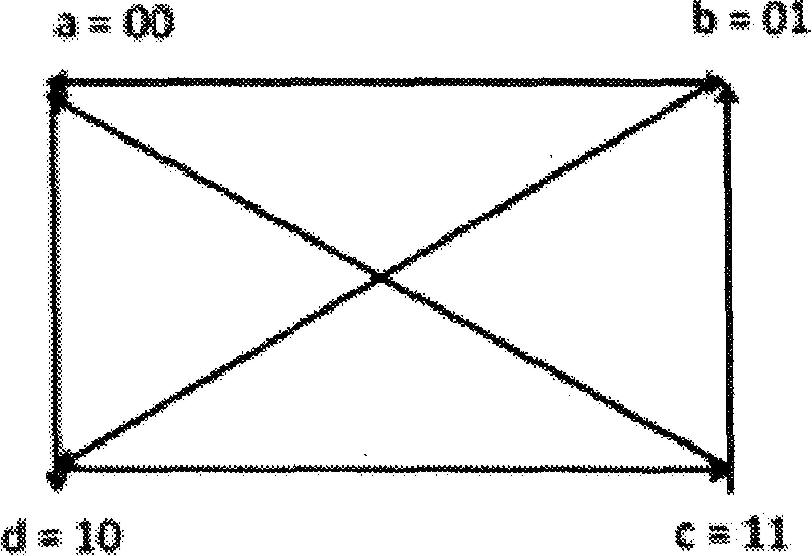
La transition de l'état « b » (01) à l'état « d » (10) et la transition de l'état « c » (11) à l'état « a » (00) montrent une condition de concurrence puisque deux états binaires sont modifiés en même temps.
Pour éviter les conditions de concurrence et obtenir une affectation sans course, nous ajouterons 3 lignes supplémentaires au tableau de flux.
Le tableau de flux de la figure est modifié en ajoutant trois lignes supplémentaires. Ces lignes sont nommées « e », « f » et « g ».
Ce tableau de flux modifié est illustré ci-dessous:
| x1x2 | ||||
| 00 | 01 | 11 | 10 | |
| a = 000 | b | a | e | a |
| b = 001 | b | d | b | a |
| c = 011 | c | g | b | c |
| g = 010 | - | a | - | - |
| - = 110 | - | - | - | - |
| f = 111 | c | - | - | c |
| d = 101 | f | d | d | f |
| e = 100 | - | - | d | - |
Le nombre total de lignes dans la table de flux est désormais de 7 (a à g), nous avons donc besoin de 3 bits pour représenter chaque ligne.
Ainsi, dans le tableau de flux de la figure les lignes nommées a, b, .. g se voient attribuer une valeur binaire de 3 bits comme indiqué ci-dessous:
a = 000, b = 001, c = 011, d= 101, e= 100, f= 111, g = 010
Désormais, la transition de l'état « a » à « d » doit désormais passer par « e ».
Cela signifie que les variables binaires passent de a = 011 à e=100 puis à d = 101.
De même, la transition de l'état « c » à « a » doit maintenant passer par « g ».
Le diagramme de transition pour le tableau de flux modifié de la figure est illustré à la figure ci-dessous:
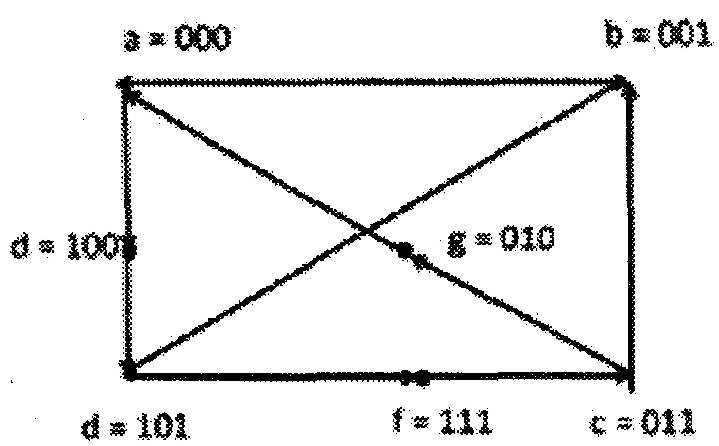
La disposition d'affectation binaire est illustrée à la figure ci-dessous: