Algèbre de Boole
Introduction
L'algèbre booléenne a été développée par le mathématicien anglais George Bole en 1854.
L'algèbre booléenne est une formulation mathématique qui traite des opérations logiques, dans lesquelles il n'y a que deux états 0 (OFF) et 1 (ON).
En algèbre mathématique normale, une variable peut avoir différentes plages de valeurs 0, 1, 2,3... et ainsi de suite, mais en algèbre booléenne, il n'y a que deux valeurs 1 (Vrai/Activé) et 0 (Faux/Désactivé).
Dans le monde d’aujourd’hui, tous les ordinateurs peuvent effectuer des opérations arithmétiques et logiques à l’aide des circuits électroniques intégrés. Ces circuits électronique utilisent la logique binaire pour effectuer différents calculs (calculs de logique arithmétique).
La logique binaire utilise uniquement deux valeurs 1 et 0, où 1 signifie une vraie valeur ou un état ON et 0 signifie une fausse valeur ou un état OFF.
Ainsi, l'algèbre booléenne est mieux adaptée à cette logique binaire et aux circuits informatiques pour effectuer diverses opérations logiques.
Outre les états booléens, il existe certaines portes logiques AND, OR, NOT, NAND, NOR qui utilisent l'algèbre booléenne pour effectuer diverses opérations logiques.
Postulats de l'algèbre booléenne
L'algèbre booléenne comprend un ensemble d'éléments, un ensemble d'opérateurs et des axiomes (ou postulats) non prouvés.
Un ensemble d’éléments est une collection d’objets possédant une propriété commune.
Supposons que nous ayons un ensemble S = {1, 3, 5, 7, 9}.
Cela implique que S est un ensemble de nombres impairs inférieurs à 10, où {1, 3, 5, 7, 9} sont les membres/éléments appartenant aux ensembles.
Si S est un ensemble quelconque et que a∈S signifie que « a » est l'élément de S ou que « a » appartient à « S » et ¬b S signifie que « b » n'est pas l'élément de S ou que « b » n'appartient pas à 'S'
L'ensemble des opérateurs de l'algèbre booléenne sont les opérateurs binaires (les opérateurs binaires opèrent sur deux variables). Les opérateurs binaires sont définis sur n'importe quel ensemble S.
Cela signifie qu'une règle est assignée à chaque paire (les opérateurs binaires opèrent sur deux variables, donc paire) d'éléments appartenant à l'ensemble S.
Par exemple, si a + b = c, alors '+ ' un opérateur binaire si 'c' peut être déterminé à partir de la paire d'éléments (a, b) et aussi si a, b ∈ S et c ¬ S.
Si l'une des conditions n'est pas satisfaite, cela signifie si a, b ∈ S mais c ¬ S , cela implique que c ne peut pas être déterminé à partir de {a, b} et donc '+' n'est pas un opérateur binaire.
De même, nous avons des opérateurs unaires (les opérateurs unaires opèrent sur une variable) en algèbre booléenne.
Les opérateurs unaires sont également définis sur n'importe quel ensemble S. Cela signifie qu'une règle est affectée à différents éléments appartenant à l'ensemble S.
Par exemple, si ~ a = b, alors "~" est un opérateur unaire si a e S et b e S .( " ~" signifie NON ou complément).
Les postulats (également appelés axiomes) sont les énoncés ou les structures de base qui sont considérés comme vrais sans preuve et ce sont les structures de base à partir desquelles il est possible de déduire les propriétés des théorèmes.
Les postulats de l'algèbre booléenne sont discutés ci-dessous et sont définis sur des éléments de l'ensemble S.
Les opérateurs binaires utilisés sont : '+' et '.'
L'opérateur unaire utilisé est '-' (lu sous forme de barre).
Postulat 1 :
(a) Fermeture par rapport à (par rapport à) l'opérateur '+'
Un ensemble 'S' est fermé par rapport à l'opérateur binaire '+' si pour chaque paire d'éléments de S l'opérateur binaire '+' obtient un élément unique de S.
Cela signifie :
Si c = a + b, alors c ∈ S pour chaque paire {a, b} ∈ S.
(b) Fermeture par rapport à l'opérateur '.'
Un ensemble 'S' est fermé par rapport à l'opérateur binaire '.' si pour chaque paire d'éléments de S l'opérateur binaire '.' obtient un élément unique de S.
Cela signifie :
Si c = a. b, alors c ∈ S pour chaque paire {a, b} ∈ S.
Supposons que nous ayons défini N = {1, 2, 3....} de nombres naturels.
Cet ensemble N est fermé par rapport à l'opérateur binaire '.'pour tout {a, b} ∈ N, puisque c = a. b, où c ∈ S .
Cet ensemble N n'est pas fermé par rapport à l'opérateur binaire ' 6 ' pour tout {a, b} ∈ N, comme pour c = ∈ 66 b, a ∈ S, b ∈ S mais 'c' peut ou non appartenir à N.
Supposons que si a= 3, b -2, alors c=a6b = 362 = 1 et tout a, b et c ∈ N.
Si supposons a = 3, b= 6 alors c=a6b = 366 = 63 .Ici a, b ∈ N mais c n'appartient pas à N
Postulat 2 :
(a) Existence de l'élément d'identité '0' par rapport (par rapport à) l'opérateur '+' dans un ensemble S tel que
x + 0 = x pour chaque élément x ∈ S.
(b) Existence de l'élément d'identité '1' par rapport à l'opérateur '.' dans un ensemble S tel que x . 1 = x pour chaque élément x ∈ S.
Postulat 3 :
Loi commutative pour x, y ∈ S
(a) x + y = y + x
(b) x. y = y . X
Postulat 4 :
Loi distributive pour x, y, z ∈ S
(a x. (y + z) = (x . y) + (x . z)
(b) x + (y . z) = (x + y) . (x + z)
Postulat 5 :
Pour un ensemble S donné d'élément x ∈ S il existe x' ∈ S (c est complémentaire de x ) tel que
(a) x + x' = 1
(b) x . x' = 0
Postulat 6 :
Pour un ensemble S donné il existe au moins deux éléments x, y ∈ S tels que x n'est pas égal à y.
Algèbre booléenne à deux valeurs
Une algèbre booléenne à deux valeurs se compose d'un ensemble S {0, 1} avec deux éléments 0 et 1, un opérateur binaire '+' qui est identique à AND (ET) et un opérateur binaire '.' ce qui est identique à OR (OU).
Il existe également un opérateur complémentaire ~ un autre symbole pour l'opérateur complémentaire est ' qui est identique à NOT (NON).
Le tableau ci-dessous montrent la règle de fonctionnement pour les opérateurs '+', '.' ', respectivement.
| x | y | x . y | x | y | x + y | x | x' | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | ||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | ||
| 1 | 0 | 0 | 1 | 0 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 |
Voici quelques points à discuter :
Deux tableaux d'algèbre booléenne à valeurs (tableaux 1.12 (a), (b) et (c)) montrent que le résultat de chaque opération est soit 0, soit 1 et 0,1 e S.
Cela signifie que la fermeture est évidente et donc les postulats 1 (a) et 1 (b) sont satisfaits.
À partir des tableaux ci-dessus, nous pouvons conclure que : x + 0 = x et x . 1 = x pour chaque élément x ∈ S
i. 0 + 0 = 0 et 1 + 0 = 1
ii. 0 . 1 = 0 et 1 . 1 = 1
Cela satisfait aux postulats 2(a) et 2(b), c'est-à-dire l'existence de l'élément d'identité '0' par rapport à opérateur '+' et existence de l'élément d'identité '1' par rapport à opérateur '.'
Loi commutative, c'est-à-dire x + y = y + x et x . y = y . x est implicite à partir de la symétrie des opérateurs binaires « + » et « . ». Le postulat 3 est donc satisfait.
Loi distributive x. (y + z) = (x . y) + (x . z) est vrai et peut être vérifié à partir de la table de vérité pour toutes les valeurs possibles de x, y et z.
De même x + (y . z) = (x + y).
(x + z) est vrai et peut être vérifié à partir de la table de vérité pour toutes les valeurs possibles de x, y et z.
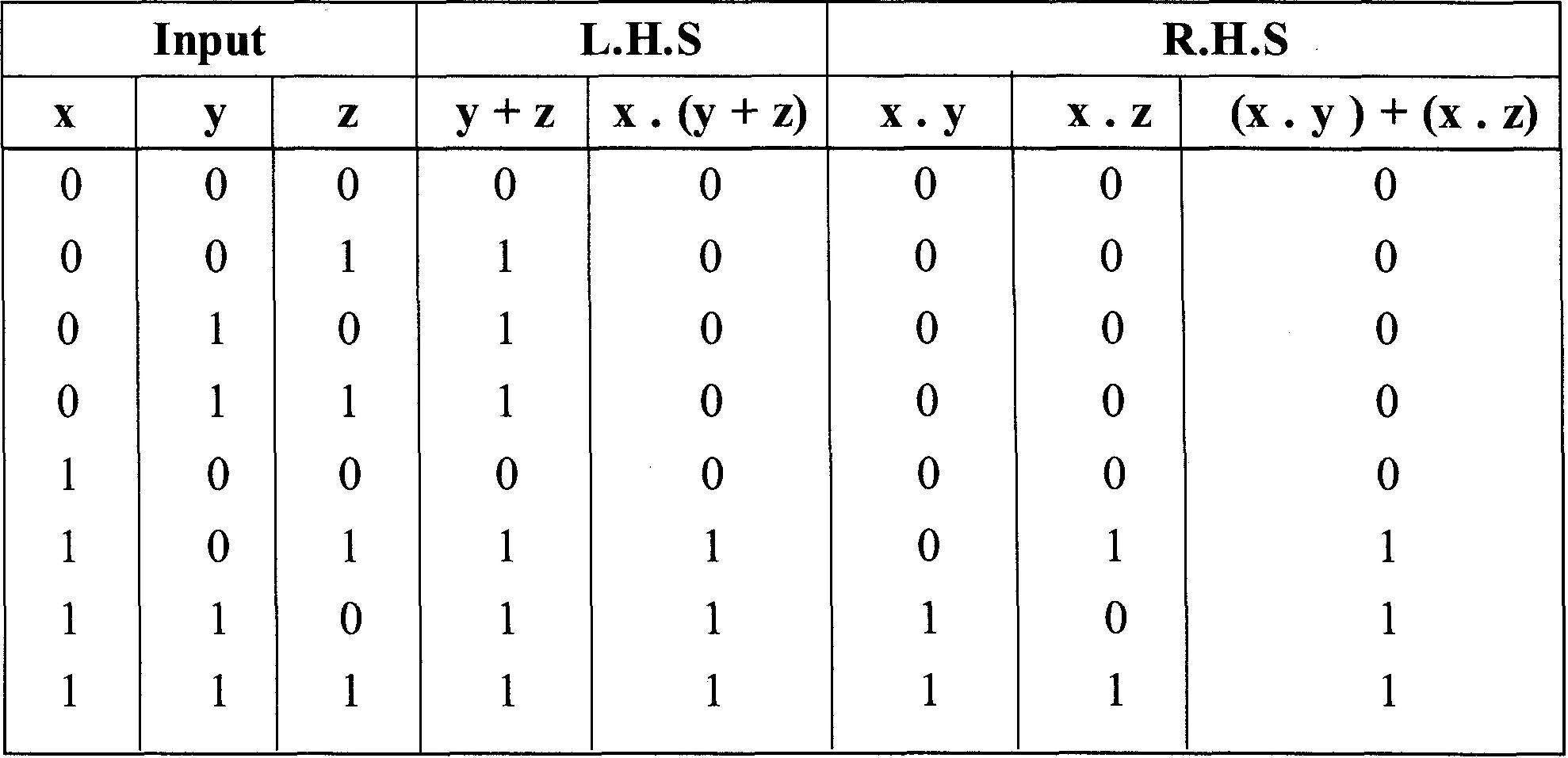
Table de vérité pour x. (y + z) = (x . y) + (x . z)

Table de vérité pour x + (y . z) = (x + y) . (x + z)
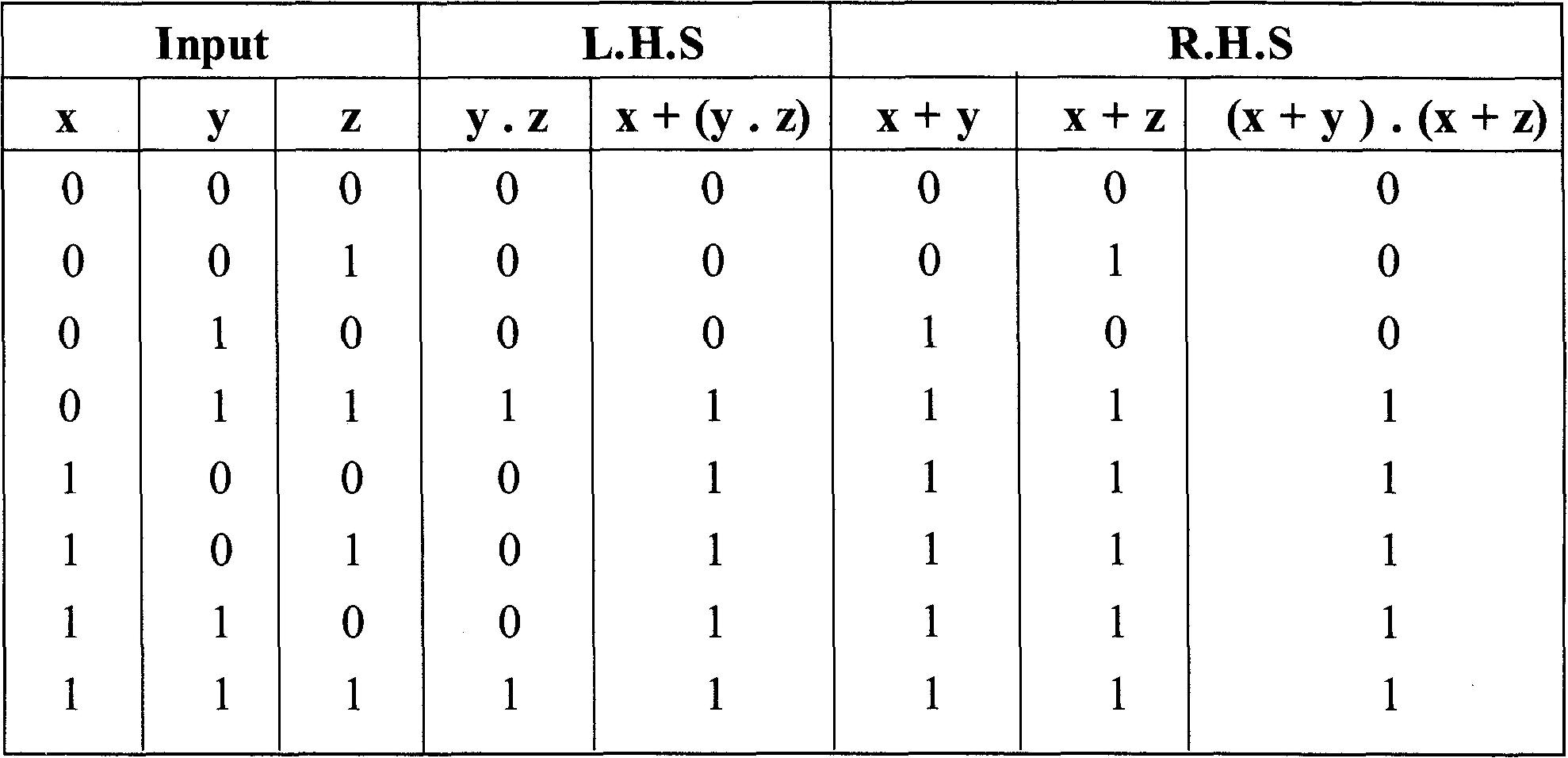
D'après les tableaux, les postulats 4 (a) et (b) sont satisfaits.
5. Du tableau complémentaire nous pouvons conclure :
a. x + x' = 1, c'est-à-dire 0 + 0' = 0 + 1 = 1 (pour x = 0)
1 + 1' = 1+0 = 1 (pour x = 1)
b. x . x' = 0, c'est-à-dire 0 . 0' = 0 . 1 = 0 (pour x = 0)
1 . 1' = 1 . 0 = 0 (pour x = 1) Le postulat 5 est donc satisfait.
6. L'algèbre booléenne à deux valeurs a défini s = {0, 1} où 0 et 1 sont deux éléments de district, ce qui signifie que 1 n'est pas égal à 0. Par conséquent, le postulat 6 est satisfait.
Principe de dualité
Le principe de dualité est l'une des propriétés importantes de l'algèbre booléenne.
Ce principe de dualité stipule que si une expression donnée est valide en algèbre booléenne, alors son dual est également une expression valide.
Par dual d'une expression, nous entendons remplacer chaque opérateur binaire '+' par l'opérateur '.', en remplaçant chaque opérateur binaire '.' avec '+', chaque '0' avec '1' et chaque '1' avec '0' dans une expression donnée et l'expression reste néanmoins valable dans une algèbre booléenne.
Supposons que nous ayons l'expression valide suivante :
(b . c) + a = (b + c) . (b + a) alors son dual est,
(b + c) . a = (b . c) + (b . a) est également une expression valide.
Chacun des postulats décrits dans la section précédente suit le principe de dualité car (a) et (b) des parties de chaque postulat sont duales, où soit les opérateurs sont interchangés (« + » avec « . » et « . » avec « + »), soit l'identité les éléments sont interchangés (1 avec « 0 » et « 0 » avec « 1 ») tout en conservant leur validité et en prouvant que le principe de dualité existe.
Théorèmes de base de l'algèbre booléenne
Les théorèmes de base de l'algèbre booléenne sont discutés ci-dessous
(ici L.H.S = côté gauche et R.H.S = côté droit)
Théorème 1 :
L.H.S. = A + A
R.H.S. = A
(a) A + A = A (Loi idempotente)
Preuve :
A + A = (A + A) . 1 -> Par postulat 2(b)
= (A + A) . (A + A') —> Par postulat 5(a)
= A + A . A' —> Par postulat 4(b)
= A + 0 -> Par postulat 5(b)
= A
Donc L.H.S = R.H.S
L.H.S. = A . A
R.H.S. = A
Théorème 1 : (b)
A . A =A (Loi idempotente)
Preuve :
A . A = (A . A) + 0 -> Par postulat 2(a)
= (A . A) + (A . A') -> Par postulat 5(b)
= A . (A + A') -> Par postulat 4(a)
= A . 1 -> Par postulat 5(a)
= A
D'où L.H.S = R.H.S
Le théorème 1(b) est dual du théorème 1(a).
L.H.S = A + 1
R.H.S = 1
Théorème 2 : (a)
A + 1 = 1 (Propriété unitaire)
Preuve :
A + 1 = (A + 1) . 1 -> Par postulat 2(b)
= (A + 1) . (A + A) -> Par postulat 5(a)
= A + (A' . 1) -» Par postulat 4(b)
= A + A' -> Par postulat 2(b)
= 1 -> Par postulat 5(a)
Donc L.H.S = R.H.S
L.H.S. = A . 0
R.H.S = 0
Théorème 2 : (b)
A . 0 = 0 (propriété zéro)
Preuve :
A . 0 = (A . 0) + 0 -> Par postulat 2(a)
= (A . 0) + (A . A') -> Par postulat 5(b)
= A . (0 + A') -> Par postulat 4(a)
= A . A' -> Par Postulat 2(a)
= 0 -> Par postulat 5(b)
Donc L.H.S = R.H.S
L.H.S. = ((A)')'
R.H.S. = A
Théorème 3 :
((A)')' =A (Loi d'Involution)
Preuve :
((A)')' = ((A )')' + 0 -> Par postulat 2(a)
= ((A)')' + (A . A) -> Par postulat 5(b)
= [((A)')'+A] . [((A))' + A'] -> Par Postulat 4(b)
= [A + ((A)')'] . [A' + ((A))'] -> Par Postulat 3 (a)
= [A+ ((A)')'] . 1 -> Par Postulat 5(a) x + x' = 1
= [A+ ((A)')'] .( A+ A') -> Par Postulat 5(a)
= A+ [((A)')' . A' ] -> Par Postulat 4(b)
= A + 0 -> Par Postulat 5(b)
= A
Donc L.H.S = R.H.S
L.H.S. = A + (A . B)
R.H.S. = A
Théorème 4 : (a)
A + (A . B) = A (loi d'absorption)
Preuve :
A + (A . B) = (A . 1) + (A . B) -> Par postulat 2(b)
= A . (1 + B) -> Par postulat 4(a)
= A . (B +1) -> Par Postulat 3 (a)
= A . 1 -> Par théorème 2(a)
= A -> Par postulat 2(b)
Donc L.H.S = R.H.S
L.H.S. = A . (A + B)
R.H.S. = A
Théorème 4 : (b)
A . (A + B) = A (loi d'absorption)
Preuve :
A . (A + B) = (A + 0) . (A + B) -> Par postulat 2(a)
= A + (0 . B) -> Par postulat 4(b)
= A . (B . 0) -> Par postulat 3(a)
= A . 0 = A
Par conséquent L.H.S = R.H.S
Le théorème 4(b) est dual du théorème 4(a).
L.H.S.
R.H.S.
Théorème 5 : (a)
A + (A . B) = A + B (Loi de réduction)
Preuve :
A + (A' . B) = (A + A') . (A + B) -> Par postulat 4(b)
= 1 . (A + B) -> Par postulat 5 (a)
= A + B -> Par postulat 2(b)
Donc L.H.S = R.H.S
L.H.S. = A . (A' + B)
R.H.S. = A
Théorème 5 : (b)
A . (A' + B) = A
Preuve :
A . (A' + B) = (A . A) + (A . B) -> Par postulat 4(a)
= 0 + (A. B) -+ Par postulat 5(b)
= A. B -» Par postulat 2(a)
Donc L.H.S = R.H.S
Théorème 6 : (a)
'+' est associatif, signifie x + (y + z) = (x + y) + z (Droit associatif)
Preuve :
Supposons L = x + (y + z) et R = (x + y) + z
Pour commencer par L.H.S,
x . L = x [ x + (y + z)]
= x . x + x . (y + z) —> Par postulat 4(a)
= x + x . (y + z) -> Par théorème 1 (a)
= x —>Par le théorème 4(a)
Donc, L.H.S = x
Maintenant R.H.S,
x . R= x [(x + y) + z]
= x . (x + y) + (x . z) -> Par postulat 4(a)
= x + x . z —> Par le théorème 4(b)
= x —> Par le théorème 4(a)
Donc R.H.S = x
Donc L.H.S = R.H.S = x
Donc x . L = x . R et par dualité x + L = x + R
Après,
Pour commencer par L.H.S,
x' . L = x' [ x + (y + z)]
= x' . x + x' . (y + z) -> Par postulat 4(a)
= 0 + x' . (y + z) -> Par postulat 5(b)
= x' . (y + z) -> Par postulat 2(a)
Donc, L.H.S = x' . (y + z)
Maintenant R.H.S.,
x' . R = x' [ (x + y) + z]
= x' . (x + y) + (x' . z) -> Par postulat 4(a)
= x' . x + x '. y + x . z -> Par postulat 4(a)
= 0 + x' . y + x '. z -> Par postulat 5(b)
= x' . y + x' . z -> Par postulat 2(a)
= x'(y + z) -> Par postulat 4(a)
Donc, R.H.S = x' . (y + z)
Donc L.H.S = R.H.S = x' . (y + z)
Donc, x' . L = x . 'R et par dualité x' + L = x' + R
Maintenant à compléter la preuve,
L = x + (y + z)
= 0 + [x + (y + z)] -> Par postulat 2(a)
= 0 + L
= (x . x') + L -> Par postulat 5(b)
= x . L + x' .L -» Par postulat 4(a)
= x . R + x' . R -> en utilisant la preuve x . L = x . R
et x' . L=x' . R
= R . (x + x') -> Par postulat 4(a)
= R -> Par postulat 5(a)
D'où L= R, signifie x + (y + z) = (x + y) + z
Théorème 6 : (b) ' . ' est associatif, signifie x . (y . z) = (x . y). z (Droit associatif)
Preuve :
Puisque le théorème 6(b) est dual du théorème 6(a), donc en utilisant la loi de dualité, le théorème 6(b) est prouvé.
Théorème 7 : a' le complément de a est unique (Unicité du complément)
Preuve : Supposons qu'il y ait deux compléments différents de a et que ceux-ci soient a1' et a2' alors,
a + a1' = 1 -> Par postulat 5(a)
a . a1' = 0 -> Par postulat 5(b)
a + a2' = 1 -> Par postulat 5(a)
a . a2' = 0 -> Par postulat 5(b)
Maintenant,
a1' = a1' . 1 -> Par postulat 2(b)
a1' . (a + a2') -> d'en haut a+ a2' = 1
= a1' . a + a1' . a2' -> Par postulat 4(a)
= a . a1 + a1 . a2' -> Par postulat 3(b)
= 0 + a1' . a2' -> d'en haut a . a1 = 0
= a . a2' + a1' . a2' -> d'en haut a . a2' = 0
= a2' . a + a2' . a1' -> Par postulat 3(b)
= a2' . (a + a1') -> Par postulat 4(a)
= a2' . 1 -> Par postulat 5(a)
= a2' -> Par postulat 2(b)
Donc a1'= a2', donc deux compléments de a sont égaux.
Le complément de a est donc unique.
Théorème 8 : (a) (a + b)' = a'b' (Loi de De-Morgan)
Preuve :
D'après le théorème 7, on sait que les compléments sont uniques
et
Par le postulat 5, nous savons que :
x + x' =1 et x . x' = 0
Maintenant, pour prouver que (a + b)' = a'b', nous devons montrer que a'b' est le complément de a + b.
Cela peut être prouvé en montrant que,
(a + b) + a'b' = 1
Et (a + b) . a'b' = 0
Nous commençons par prouver d'abord (a + b) + a'b' = 1
Commencez par L.H. S = (a + b) + a'b'
(a + b) + a'b' - [(a + b) + a'] . [(a + b) + b'] -> Par postulat 4(b)
= [(b +a) + a'] . [(a + b) + b'] -> Par postulat 3(a)
= [(b + (a + a')] . [(a + (b + b')] -> Par théorème 6(a)
= (b + 1) . (a + 1) -> Par postulat 5(a)
= 1 . 1 -> Par théorème 2(a)
= 1 -> Par théorème 1(b)
L.H.S = 1
Donc L.H.S = R.H.S
Ainsi (a + b) + a'b' = 1
Nous allons maintenant prouver (a + b) . a'b' = 0
Commencez par L.H.S = (a + b) . a' b'
(a + b) . a'b' = a' . b' . (a + b) -> Par postulat 3(b)
= [(a' . b') . a] + [(a' . b') . b] -> Par postulat 4(a)
= [(b' . a') . a] + [(a' . b') . b] -> Par postulat 3(b)
= (b' . (a' . a)] + [a' . (b' . b)] -> Par théorème 6(b)
= (b' . 0) + (a' . 0) -> Par postulat 5(b)
= 0 + 0 -> Par Théorème 2(b)
= 0 -> Par le théorème 1 (a)
L.H.S = 0
Donc L.H.S = R.H.S
Ainsi (a + b) . a'b' = 0
D'où la loi de De-Morgan (a + b)' = a'b' est prouvée
Théorème 8 (b) : (a . b)' = a' + b' (Loi de De-Morgan)
Preuve :
Puisque le théorème 8(b) est dual du théorème 8(a), donc par la loi de dualité le théorème 8(b) est prouvé.
