Circuit avec Latch
Logique séquentielle asynchrone
Dans cette section, nous discuterons du verrou SR avec des portes NOR et du verrou SR avec des portes NAND. Ensuite, nous prendrons un exemple de conception de circuit logique séquentiel asynchrone utilisant le verrou SR.
Nous aborderons également plus en détail : la table d'excitation du verrou et la dérivation d'un circuit de verrouillage à partir d'une table de transition.
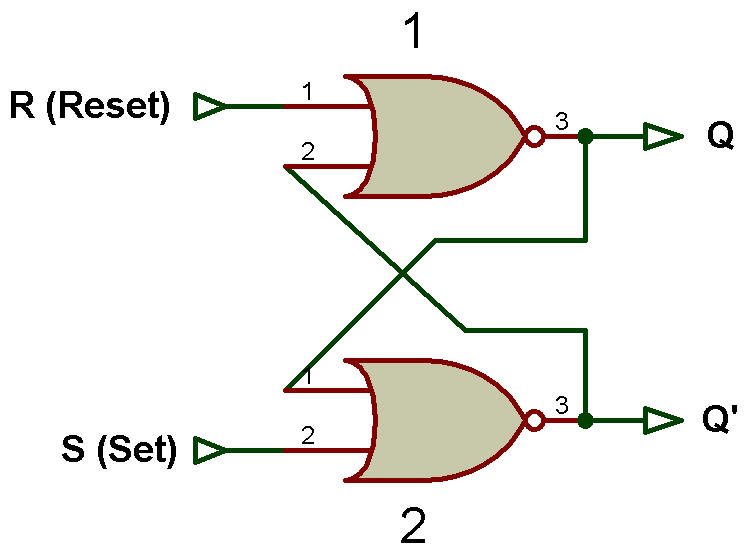
Verrouillage SR avec portes NOR
Nous savons que le verrou SR est un circuit numérique composé de deux entrées S et R et de deux portes NON-OU à couplage croisé ou de deux portes NAND à couplage croisé (le verrou SR a déjà été discuté en détail dans l'unité 3, section 3.2.1).
La figure ci-dessous montre le verrou SR avec des portes NOR.

La table de vérité pour le verrou SR avec portes NOR est présentée dans le tableau ci-dessous
Ce tableau est identique au tableau pour le verrou SR avec portes NOR dans la section Latch (Verrous).
| Entrées | Sorties | |||
| S | R | Q | Q' | Description |
| 1 | 0 | 1 | 0 | SET |
| 0 | 0 | 1 | 0 | La sortie ne change pas (la sortie précédente est conservée) |
| 0 | 1 | 0 | 1 | RESET |
| 0 | 0 | 0 | 1 | La sortie ne change pas (la sortie précédente est conservée) |
| 1 | 1 | 0 | 0 | État INTERDIT (INVALIDE) |
La figure ci-haut est redessinée comme le montre la figure ci-dessous:
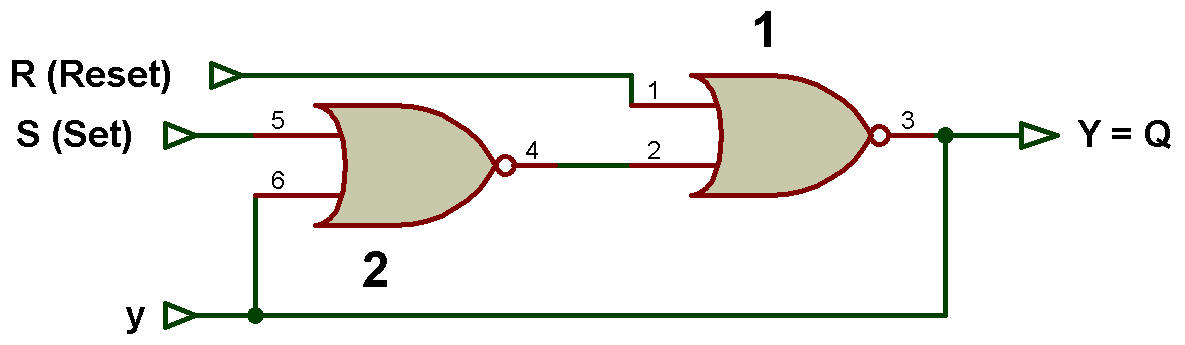
Dans la figure, le chemin de rétroaction va de la sortie de la porte NON-OU 1 à l'entrée de la porte NON-OU 2.
La sortie Q est égale à la variable d'excitation Y et à la variable secondaire y, ce qui signifie : Y = y = Q.
D'après la figure,
Y= [(S + y)' + R]'
Soit (S + y)' = a et R = b, donc Y = ( a + b)' = a'.b' -> Parce que (x + y)' = x' . y' selon le théorème de De-Morgan
En remplaçant la valeur de a et b, nous obtenons,
Y = a' . b' = ((S + y)')' . R' = (S + y) . R' = SR' + yR'
La figure ci-dessous montre le tableau de transition. La table de transition précise la valeur de Y par rapport aux entrées « y » et SR.
| SR | ||||||
| C1 | C2 | C3 | C4 | |||
| 00 | 01 | 11 | 10 | |||
| y | R1 | y' (0) | 0 | 0 | 0 | 1 |
| R2 | y (1) | 1 | 0 | 0 | 1 | |
Ainsi à partir de la table de transition Y = SR' + yR'
Pour SR', voir Première rangée, quatrième colonne (R1C4) et Deuxième rangée, quatrième colonne (R2C4).
Marquez « 1 » à ces deux endroits.
Pour yR', voir Deuxième rangée, première colonne (R2C1) et Deuxième rangée, quatrième colonne (R2C4).
Marquez '1' à ces deux endroits (notez que la deuxième rangée, la quatrième colonne (R2C4) a déjà été marquée '1' par SR').
À partir de la table de vérité présentée dans le tableau, nous pouvons noter que lorsque S = R = 1, Q et Q' deviennent tous deux « 1 ».
Ceci n’est pas valide car Q et Q’ sont complémentaires l’un de l’autre.
Pour éviter cette condition, nous pouvons poser la condition suivante :
ANDing de S et R doit toujours être '0' signifie SR = 0 dans tous les cas.
Cela signifie que R et S ne peuvent pas être « 1 » en même temps.
Si SR = 0, alors SR' = S.
Voir le tableau ci-dessous pour comprendre cela.
| Entrées | Sorties | ||
| S | R | R' | SR' |
| 0 | 0 | 1 | 0 (S) |
| 0 | 1 | 0 | 0 (S) |
| 1 | 0 | 1 | 1 (S) |
SR Latch avec portes NAND
La figure ci-dessous montre le verrou SR avec des portes NAND.
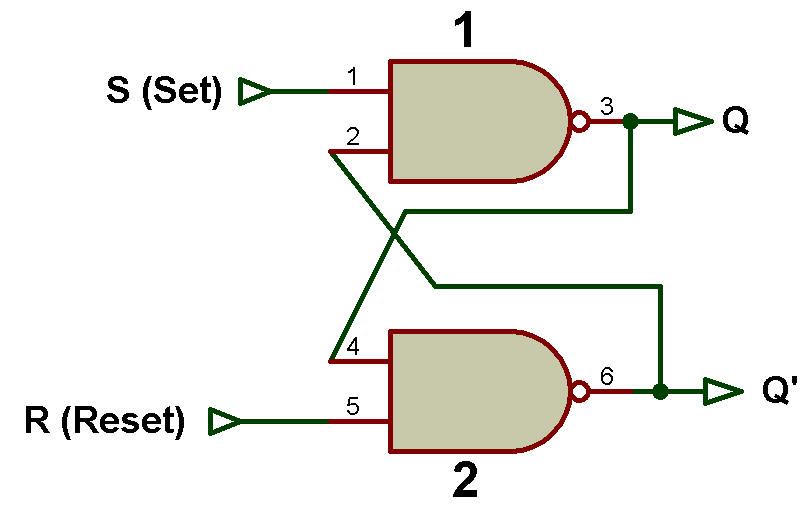
La table de vérité pour le verrou SR avec portes NAND est présentée dans le tableau ci-desous. Ce tableau est identique au tableau pour le verrou SR avec portes NAND dans la section Latch (Verrous).
| Entrées | Sorties | |||
| S | R | Q | Q' | Description |
| 0 | 1 | 1 | 0 | SET |
| 1 | 1 | 1 | 0 | La sortie ne change pas (la sortie précédente est conservée) |
| 1 | 0 | 0 | 1 | RESET |
| 1 | 1 | 0 | 1 | La sortie ne change pas (la sortie précédente est conservée) |
| 0 | 0 | 1 | 1 | État INTERDIT (INVALIDE) |
La figure ci-haut est redessinée comme le montre la figure ci-dessous:
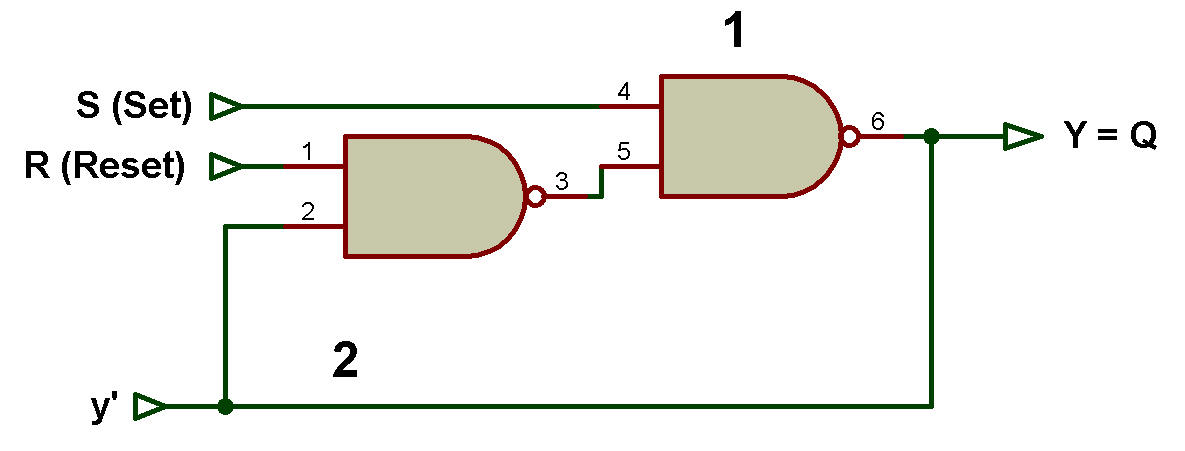
Dans la figure, le chemin de rétroaction va de la sortie de la porte NAND 1 à l'entrée de la porte NAND 2.
La sortie Q est égale à la variable d'excitation Y et à la variable secondaire y, ce qui signifie :
Y = y = Q.
D'après la figure
Y=[(S(Ry)']'
Soit S = a et (Ry)' = b, donc Y = (a . b)' = a' + b' [car (x . y)' = x' + y' selon le théorème de De-Morgan
En remplaçant la valeur de a et b, nous obtenons, Y = a' + b' = S' + ((Ry)')' = S' + Ry
Le tableau ci-dessous montre le tableau de transition.
| SR | ||||||
| C1 | C2 | C3 | C4 | |||
| 00 | 01 | 11 | 10 | |||
| y | R1 | y' (0) | 1 | 1 | 0 | 0 |
| R2 | y (1) | 1 | 1 | 1 | 0 | |
La table de transition précise la valeur de Y par rapport aux entrées y et SR.
Ainsi à partir de la table de transition : Y = S' + Ry
Pour S', voir R1C1, R1C2, R2C1 et R2C2.
Marquez un 1 à tous ces endroits.
Pour Ry, voir R2C2 et R2C3. Marquez '1' à ces deux endroits (Notez que R2C2 a déjà été marqué '1' par S).
Exemple de circuit avec SR Latch
Prenons l'exemple de la conception d'un circuit logique séquentiel asynchrone utilisant le verrou SR.
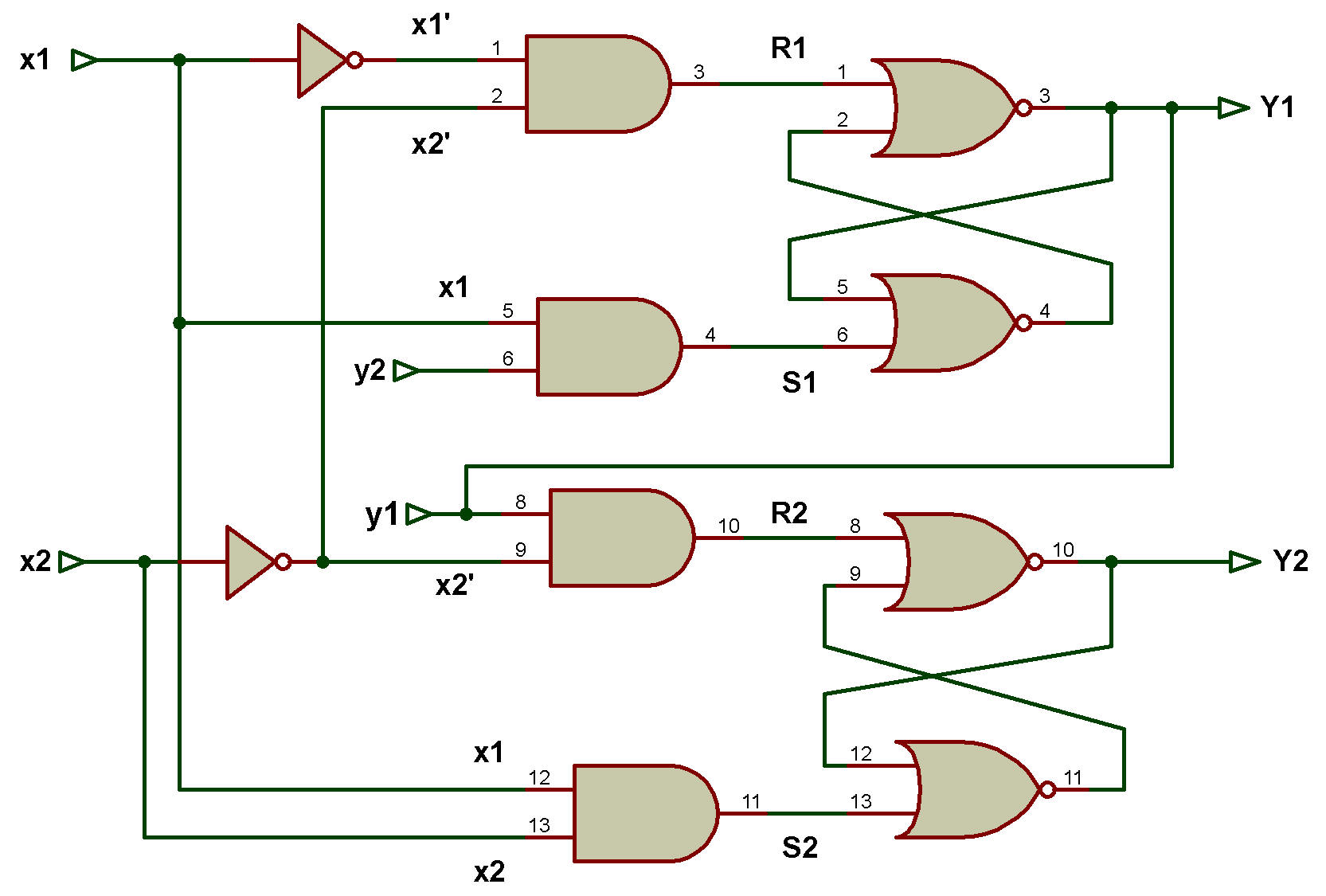
La figure ci-dessous montre un circuit logique séquentiel asynchrone construit à l'aide de deux verrous SR avec des portes NOR.
Dans la figure, il y a :
• Deux variables d'entrée principales : x et x2.
• Deux variables d'entrée secondaires : y et y2.
• Deux variables d'excitation : Y et Y2.
Circuit logique séquentiel asynchrone construit à l'aide de deux verrous SR avec portes NOR
La figure ci-dessous montre le tableau de transition pour Y1
| x1x2 | ||||||
| C1 | C2 | C3 | C4 | |||
| x1'x2' | x1'x2 | x1x2 | x1x2' | |||
| y1y2 | R1 | y1'y2' | 0 | 0 | 0 | 0 |
| R2 | y1'y2 | 0 | 0 | 1 | 1 | |
| R3 | y1y2 | 0 | 1 | 1 | 1 | |
| R4 | y1'y2' | 0 | 1 | 1 | 1 | |
La figure ci-dessous montre le tableau de transition pour Y2.
| x1x2 | ||||||
| C1 | C2 | C3 | C4 | |||
| x1'x2' | x1'x2 | x1x2 | x1x2' | |||
| y1y2 | R1 | y1'y2' | 0 | 0 | 1 | 0 |
| R2 | y1'y2 | 1 | 1 | 1 | 1 | |
| R3 | y1y2 | 0 | 1 | 1 | 0 | |
| R4 | y1'y2' | 0 | 0 | 1 | 0 | |
La table de transition pour Yt et Y2 est combinée pour obtenir la table de transition pour Y.
La figure ci-dessous montre la table de transition pour Y.
| x1x2 | ||||||
| C0 | C10 | C11 | C12 | |||
| x1'x2' | x1'x2 | x1x2 | x1x2' | |||
| y1y2 | R0 | y1'y2' | 00 | 00 | 01 | 00 |
| R10 | y1'y2 | 01 | 01 | 11 | 11 | |
| R11 | y1y2 | 00 | 11 | 11 | 10 | |
| R12 | y1'y2' | 00 | 10 | 11 | 10 | |
Combinez la valeur binaire de la première ligne, première colonne (r1c1) de la table de transition pour Y1 avec la valeur binaire de la première ligne, première colonne (r5c5) de la table de transition pour Y2 pour obtenir la valeur binaire 00 dans la première ligne, première colonne (r9c9) pour la table de transition pour Y.
De même, combinez la valeur binaire de la première colonne de la deuxième ligne (r2c2) de la table de transition pour Y1 avec la valeur binaire de la première colonne de la deuxième ligne (r6c5) de la table de transition pour Y2 pour obtenir la valeur binaire 01 à la deuxième ligne, première colonne (r10c9) pour la table de transition pour Y et de la même manière, d'autres valeurs de la table de transition Y peuvent être déterminées.
Tableau d'excitation des verrous
Le fonctionnement de SR Latch peut facilement être compris en voyant sa table de transition.
La figure ci-haut montre la table de transition pour le verrou SR avec des portes NOR et la figure ci-haut montre la table de transition pour le verrou SR avec des portes NAND.
La table de transition spécifie la valeur binaire de la variable d'excitation « Y » lorsque les entrées S et R et la variable d'entrée secondaire y sont connues.
Mais lorsque nous procédons à la mise en œuvre d'un circuit donné, la plupart du temps, la table de transition du circuit est donnée et nous devons trouver les valeurs de S et R. Pour cette raison, nous avons besoin d'une table d'excitation.
Le tableau d'excitation montre la valeur binaire de l'entrée Sand R pour toutes les transitions (changements) possibles d'états de y (état actuel) à Y (état suivant).
Le tableau d'excitation pour le verrou SR est présenté dans le tableau ci-dessous:
|
Y État actuel |
Y État suivant |
S | R |
| 0 | 0 | 0 | x |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | x | 0 |
Pour dériver le schéma logique d'un circuit séquentiel asynchrone à partir d'une table de transition donnée :
Dans cette section, nous verrons comment dériver le schéma logique de tout circuit séquentiel asynchrone, lorsque la table de transition pour ce circuit est donnée.
Le schéma logique sera construit à l'aide de portes et de verrous SR.
Pour ce faire, prenons la table de transition comme indiqué sur le tableau ci-dessous:
| x1x2 | ||||||
| C1 | C2 | C3 | C4 | |||
| x1'x2' | x1'x2 | x1x2 | x1x2' | |||
| Y | R1 | Y' | 0 | 0 | 0 | 1 |
| R2 | Y | 0 | 0 | 1 | 1 | |
À partir des informations données dans le tableau de transition et du tableau d'excitation du verrou présenté dans le tableau ci-haut, nous pouvons dessiner la K-Map pour les entrées S et R latch.
Notez que - les valeurs binaires affichées dans le tableau de transition sont Y.
K-Map pour S et R sont illustrés respectivement aux ci-desous:
| K-Map pour S | K-Map pour R | ||||||||
| x1x2 | |||||||||
| 00 | 01 | 11 | 10 | 00 | 01 | 11 | 10 | ||
| Y | 0 | 0 | 0 | 0 | 1 | x | x | x | 0 |
| 1 | 0 | 0 | x | x | 1 | 1 | 0 | 0 | |
Les valeurs affichées dans K-Map pour S et R sont : 0, 1 et x (peu importe, cela peut être 0 ou 1).
Ces valeurs de S et R sur K-Map sont obtenues comme expliqué ci-dessous.
Voir Première ligne, première colonne du tableau de transition, comme indiqué dans le tableau ci-haut.
Nous constatons que la transition (changement) requise est y = 0 à Y = 0.
À partir du tableau d'excitation pour le verrou SR, nous constatons que S = 0 et R = x (voir la première ligne du tableau) pour cette transition requise, y = 0 à Y = 0.
Donc,
Première ligne, première colonne de K-Map pour S a la valeur 0
et première ligne, première colonne de K-Map pour R a la valeur x
De même,
À partir de la deuxième ligne et de la première colonne du tableau de transition, comme le montre la figure, nous constatons que la transition (changement) requise est y = 1 à Y = 0.
À partir du tableau d'excitation pour le verrou SR, nous constatons que S = 0 et R = 1 (voir la troisième rangée du tableau) pour cette transition requise y = 1 à Y = 0.
Donc,
La première colonne de la deuxième ligne de K-Map pour S a la valeur 0 et la première colonne de la deuxième ligne de K-Map pour R a la valeur 1.
De même, d'autres valeurs de S et R sur K-Map peuvent être trouvées.
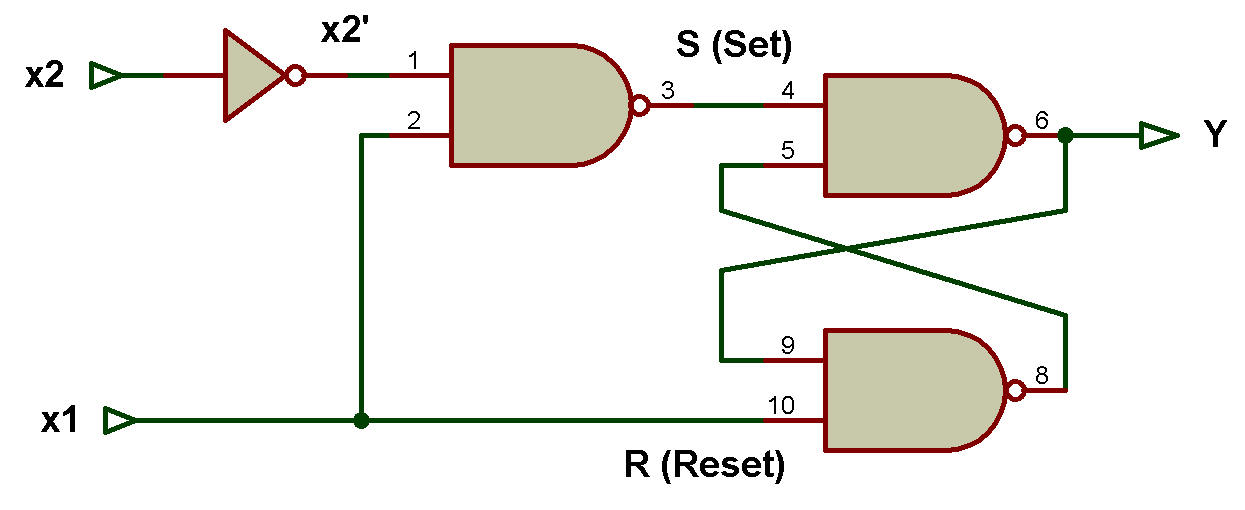
Fonction booléenne pour S = x1x2'
Fonction booléenne pour R = x1'
Le schéma logique est maintenant dessiné à l'aide des verrous SR et des portes logiques qui implémentent les fonctions booléennes S et R.
Le schéma logique pour implémenter un circuit séquentiel asynchrone avec des verrous SR utilisant des portes NOR est présenté dans la figure ci-dessous:
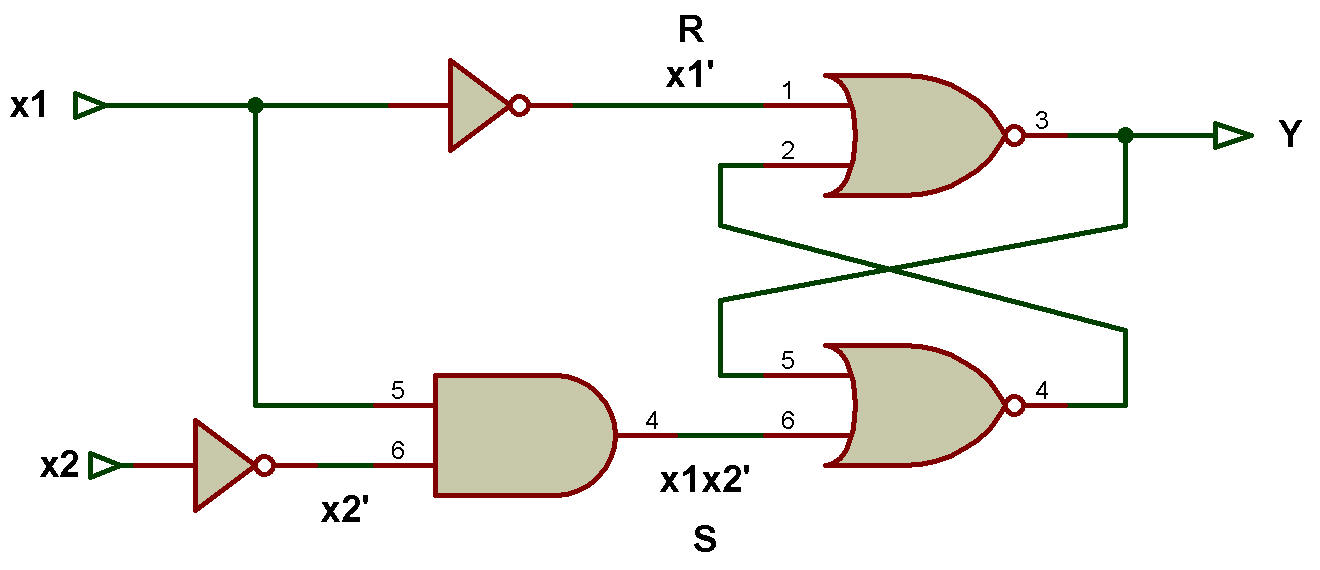
Le schéma logique pour implémenter un circuit séquentiel asynchrone avec des verrous SR utilisant des portes NAND est présenté dans la figure ci-dessous.
La valeur booléenne de S = [(x1x2')'] et la valeur booléenne de R = [x1']' = x1.