n (position du bit) :
m + k code :

Code d'erreur
Chaque fois que des données ou un message sont transmis d'un bout à l'autre, il est possible que du bruit ou une autre interruption modifie les données, c'est-à-dire que « 1 » peut devenir « 0 » ou « 0 » peut devenir « 1 ». Ce changement de données est appelé erreur.
Afin de détecter si une erreur s'est produite dans les données, nous disposons de codes de détection d'erreurs.
Ceux-ci sont:
Code de parité.
Parité de bloc.
Checksum et CRC.
Discutons de chacun d’eux un par un.
Code de parité pour la détection d'erreurs
Le code de parité pour la détection des erreurs est l'une des techniques les plus simples utilisées pour détecter toute erreur dans les données.
Dans cette technique, un bit supplémentaire, appelé bit de parité, est ajouté à chaque mot/donnée transmis. La parité peut être une parité impaire ou même une parité.
En parité impaire, le bit de parité est mis à 0 ou 1 à l'extrémité de transmission de sorte que le nombre total de 1 dans le mot/les données transmis, y compris le bit de parité, soit impair.
Par exemple, nous avons les données 10111, puis le bit de parité est défini sur 1, de sorte que le nombre total de 1 dans le mot/les données transmis, y compris le bit de parité, est impair (dans ce cas 5), comme indiqué ci-dessous.
| Parité | Bits de donné | ||||
| 1 | 1 | 0 | 1 | 1 | 1 |
Par exemple, si le mot/données est 101111, alors Parité = 0 comme indiqué ci-dessous.
| Parité | Bits de donné | |||||
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
En parité paire, le bit de parité est réglé sur 0 ou 1 à l'extrémité de transmission de sorte que le nombre total de 1 dans les données/mots transmis, y compris le bit de parité, soit pair.
Par exemple, si mot/données 1011110, alors la parité = 1, de sorte que le total des 1 soit paire comme indiqué ci-dessous.
| Parité | Bits de donné | |||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
Par exemple, si mot/données 1110111101, alors Parité = 0 comme indiqué ci-dessous.
| Parité | Bits de donné | |||||||||
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
Lorsque les données/mots sont reçus du côté du récepteur, le nombre total de 1 est vérifié.
Si le nombre total de 1 est pair pour un code de parité impair, il y a une erreur dans le mot/les données reçus.
Si le nombre total de 1 est impair pour un code de parité pair, alors les données reçues ne sont pas correctes.
Les codes de parité (pair ou impair) peuvent détecter une erreur sur un seul bit mais pas plus d'une erreur de 1 bit dans le mot transmis.
Parité de bloc
Lorsque des mots binaires sont transmis ou reçus successivement les uns après les autres, cet ensemble de bits est considéré comme un bloc de données/mots.
Chaque bloc de mot forme ainsi une ligne et une colonne. Supposons qu'à la fin de la transmission, quatre mots de 8 bits soient transmis successivement, formant ainsi 4x8 blocs, comportant 4 lignes et 8 colonnes.
Désormais, les bits de parité sont ajoutés à la fois aux lignes et aux colonnes. L'ajout de parité aux lignes et aux colonnes permet de détecter 2 erreurs dans un mot et de corriger toute erreur survenue dans les données.
Par exemple, nous avons un bloc de 4x8 données/mot à transmettre à l'extrémité de transmission.
Maintenant, des bits de parité sont ajoutés. Soit nous pouvons opter pour une parité paire, soit une parité impaire.
Ici, nous optons pour une parité paire afin que la parité paire soit maintenue à la fois par ligne et par colonne.
Désormais, le bloc est transmis sous forme de bloc 5x9 (1 bit de parité est augmenté par ligne et par colonne).
Supposons que nous ayons un bloc de 4x8 mots. Après avoir ajouté un bit de parité pour maintenir une parité paire, le bloc devient 5x9 mots, comme indiqué dans le tableau.
Ceci est résumé dans les tableaux ci-dessous.
| Bits de donné |
Parité de colonne |
||||||||
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | |
|
Parité de ligne |
0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | |
Tableau ci-dessous Erreur détectée
| Bits de donné |
Parité de colonne |
|||||||||
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | Er | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | ||
|
Parité de ligne |
0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | ||
| Er | ||||||||||
L'erreur dans le tableau se trouve dans la 2e ligne et la 3e colonne.
Cette erreur peut être corrigée en inversant le bit incorrecte. Dans ce cas, le bit d'erreur 0 doit être mis à 1, de sorte que les bits de parité par ligne et par colonne soient corrects.
Supposons que nous ayons une erreur de 2 bits dans deux colonnes différentes et une ligne, comme indiqué dans le tableau ci-dessous. Ces erreurs peuvent être détectées, mais ne peuvent pas être corrigées.
L'erreur du tableau ci-dessous est une erreur sur un seul mot.
| Bits de donné |
Parité de colonne |
||||||||
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
|
Parité de ligne |
0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | |
| Er | Er | ||||||||
Le tableau montre les erreurs de parité dans les 2e et 3e colonnes. Cela signifie qu'une erreur s'est produite dans un mot.
Puisque la parité des lignes est correcte, nous pouvons détecter ces deux erreurs mais ne pouvons pas la corriger puisqu’une ligne comporte deux erreurs.
Somme de contrôle et CRC (Contrôle de redondance cyclique)
La somme de contrôle (ou somme de hachage) est utilisée pour détecter une erreur ayant pu se produire lors de la transmission ou du stockage de blocs de données.
La somme de contrôle est formée en additionnant tous les bits d'un mot transmis particulier (bloc de données), en ignorant toute retenue générée. La somme résultante est stockée et en fin de transmission, cette somme (appelée somme de contrôle) est également transmise.
À la réception, le récepteur peut également calculer la somme de tous les mots transmis (bloc de données) et comparer cette somme avec la somme (somme de contrôle) envoyée à la fin par l'émetteur avec les données (mot).
Si cette somme correspond, il n'y a pas d'erreur, sinon le récepteur demande la retransmission de ce bloc de données particulier (mot).
CRC (Cyclic Redundancy Check) est une autre méthode pour détecter les erreurs dans les blocs de données. Il s’agit d’une technique basée sur l’arithmétique polynomiale.
Ici, les données (mot) sont traitées comme un polynôme et divisées par un polynôme générateur (une constante). Ce polynôme générateur est une constante convenue par l'émetteur et le récepteur selon les normes CRC.
Exemple :
Pour un CRC 16 bits, le polynôme générateur sera également de 16 bits.
Le mot transmis est divisé par générateur (constant) à l'extrémité de la transmission, le reste obtenu de cette division est également transmis à la fin avec le mot original (mot qui vient d'être divisé à l'aide du générateur).
Du côté du récepteur, les données reçues sont à nouveau divisées par un polynôme générateur mutuellement convenu (constant). Le reste est vérifié avec le reste transmis.
S'il correspond, il n'y a pas d'erreur, sinon le mot entier doit être à nouveau transmis par l'émetteur. Cette technique est utilisée pour détecter les erreurs dans le stockage des données sur disque dur/disques optiques.
Codes de correction d'erreur
Les codes correcteurs d'erreurs détectent non seulement les erreurs, mais les corrigent également. Le code Hamming est l'un des codes correcteurs d'erreurs.
Code Hamming pour la correction des erreurs
Dans le code de Hamming, les bits de parité sont ajoutés aux données d'origine de manière à former des données composites dans lesquelles il est non seulement possible de détecter une erreur, mais également de trouver l'emplacement de l'erreur afin que l'erreur puisse être corrigée.
Supposons que nous ayons des données originales de "m" bits.
Maintenant, selon le format de code de Hamming, les bits de parité "k" notés P1, P2, ..., Pk sont ajoutés à ces données de bits "m" depuis la gauche de manière à former un code composite de bits "m + k".
Les positions des bits dans le code "m + k" sont numérotées 1, 2, 3 4,.... en partant de la gauche.
La forme généralisée du code « m + k » est illustrée dans la figure ci-dessous.
|
n (position du bit) : m + k code : |
 |
Ici, « P » désigne le bit de parité et « D » désigne le bit de données.
D'après une forme généralisée, il est clair que les positions 1,2,4, 8,16,... sont toutes puissances de 2 et que toutes ces positions sont occupées par des bits de parité, alors que les positions 3, 5, 6, 7,10,11, 12, 13, 15,.... sont occupés par des bits de données.
Pour une donnée de 4 bits D1, D2, D3 et D4 nous avons besoin de 3 bits de parité P1, P2 P3 (voir positions 20 21 22) comme indiqué ci-dessous.
Ici m = 4 et k= 3.
Pour déterminer la valeur de k, nous voyons le bit de parité le plus élevé avant le dernier bit de données. Dans ce cas, le dernier bit de données est D4.
La parité la plus élevée avant D4 est P3. Pk = P3, donc k = 3. D'où m + k = code à 7 bits.
20 21 22
(position du bit) : 12 3 4 5 6 7
m + k code : P1 P2 D1 P3 D2 D3 D4
Cela forme un code de Hamming à 7 bits.
Une fois le code de Hamming formé, chaque bit de parité P1 P2, ... .Pk est regroupé avec certains bits de données du code et le bit de parité est mis à 0 ou 1 de sorte que le bit de parité ainsi que les bits de données forment des bits spécifiques de parité (pair ou impair selon ce qui est requis).
La règle pour former un groupe de parité avec des bits de données est :
Pour former le groupe pour Pk (où k = 1, 2, 3.....), ajoutez des bits "n-1" après Pk (ici n est la position du bit de puissance 2 pour Pk).
Sautez maintenant bits "n" bits, puis ajoutez "n" bits alternativement.
Pour k =1, Pk = P1
n = 1 et n -1 = 0.
Pour former le groupe pour P1, ajoutez le bit "n -1 = 0" après P1.
Sautez maintenant les bits "n =1" puis ajoutez alternativement les bits "n =1".
Ainsi, les nouveaux sont
P1 D1 D2 D3 D4 D5 .... (Voir Figure ci-haut).
Pour k=2, Pk=P2
n = 2 et n -1 = 1.
Pour former le groupe pour P2, ajoutez le bit "n -1 = 1" après P2.
Sautez maintenant les bits "n = 2" puis ajoutez alternativement les bits "n = 2".
Ainsi, les nouveaux sont
P2 D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 ... (Voir Figure Voir Figure ci-haut).
Pour k=3, Pk=P3
n = 4 et n -1 = 3.
Pour former le groupe pour P3, ajoutez "n -1 = 3" bits après P3.
Sautez maintenant les bits "n = 4" puis ajoutez alternativement les bits "n = 4".
Ainsi, les nouveaux sont
P3 D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 .... (Voir Figure ci-haut)
Pour k=4, Pk=P4
n = 8 et n -1 = 7.
Pour former le groupe pour P4, ajoutez des bits "n -1 = 7" après P4.
Sautez maintenant les bits "n = 8" puis ajoutez alternativement les bits "n = 8".
Ainsi, les nouveaux sont
P4 D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 ....(Voir Figure ci-haut)).
Pour détecter et corriger une erreur à l'aide de groupes de parité
Supposons que nous ayons le code 0011 à 4 bits.
Pour maintenir une parité paire, des bits de parité sont ajoutés à ce code à 4 bits.
Après avoir ajouté les bits de parité P1 P2 et P3 à ce code de 4 bits, nous obtenons un code de jambon de 7 bits 1000011.
Supposons maintenant que lors de la transmission, ce code de hamming de 7 bits devient 1000111.
Pour détecter et corriger l'erreur, groupe de parité pour P1 P2 et P3 sont vérifiés.
Le groupe de parité pour P1 est P1 D1 D2 D4 , pour P2 est P2 D1 D3 D4 et pour P3 est P3 D2 D3 D4 .
Prenons trois autres variables A, B et C.
Si la parité paire est maintenue par P3, alors définissez A = 0, sinon si la parité est perturbée, définissez A = 1.
De même, si la parité paire est maintenue par P2, alors définissez B = 0, sinon si la parité est perturbée, définissez B = 1 et de même, si la parité paire est maintenue par P1, définissez C = 0, sinon si la parité est perturbée, définissez C = 1.
Maintenant examinons ABC.
Supposons que si ABC = (100)2 = (4)10, cela signifie que le 4ème bit du MSB (à droite) doit être corrigé.
Dans notre exemple,
Le code Hamming d'origine était : 1000011.
|
n (position du bit) : m + k code : Code Hamming transmis : |
 |
Groupe de parité pour P1 : P1 D1 D2 D4 = 1011
La parité paire est perturbée donc C = 1
Groupe de parité pour P2 : P1 D1 D3 D4 = 0 0 11
La parité paire est perturbée donc B = 0
Groupe de parité pour P3 : P1 D2 D3 D4 = 0 111
La parité paire est perturbée donc A = 1
Maintenant ABC = (101)2 = (5)10, cela signifie que dans le code de hamming transmis, le 5ème bit du MSB (à droite) doit être corrigé.
Code Hamming transmis : 1000111
Après avoir corrigé le 5ème bit, nous avons : 1000011. Cela équivaut au code hamming original 1000011.
De même, nous avons un code Hamming 15 bits et un code Hamming 12 bits.
Ceux-ci sont discutés ci-dessous.
|
n (position du bit) : m + k code : |
 |
Pour déterminer la valeur de k, nous voyons le bit de parité le plus élevé avant le dernier bit de données.
Dans ce cas, le dernier bit de données est D11
La parité la plus élevée avant D11 est P4.
Pk = P4, donc k= 4 et m = 11.
Maintenant m + k = 11 + 4 = code de 15 bits.
Code Hamming 12 bits :
|
n (position du bit) :
|
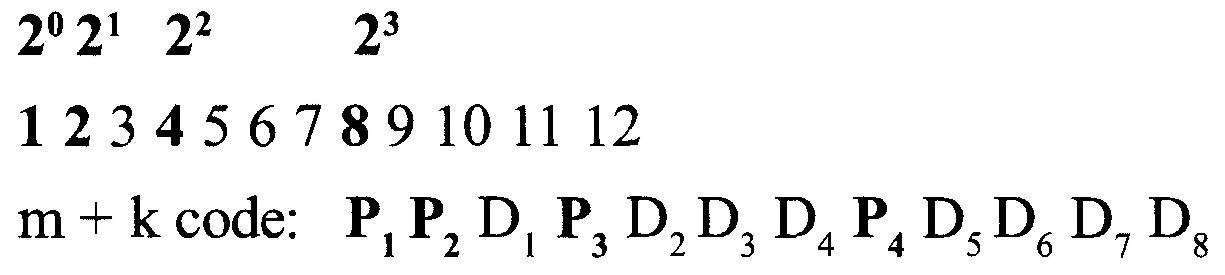 |
Pour déterminer la valeur de k, nous voyons le bit de parité le plus élevé avant le dernier bit de données.
Dans ce cas, le dernier bit de données est D8.
La parité la plus élevée avant D8 est P4.
Pk = P4, donc k= 4 et m = 8.
Maintenant m + k = 8 + 4 = code 12 bits.
