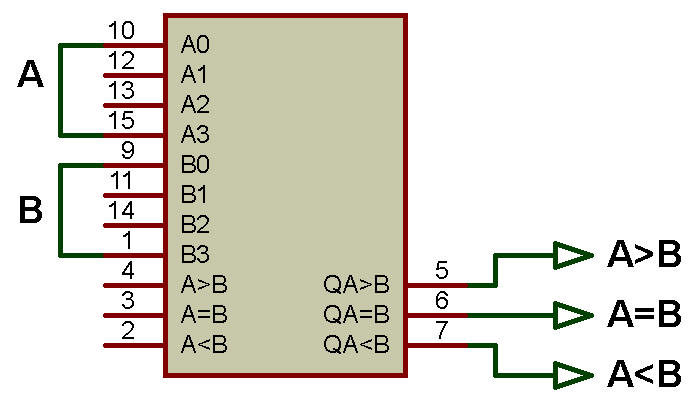
Comparateur
Un comparateur également connu sous le nom de comparateur numérique ou comparateur de magnitude est un circuit combinatoire qui compare la magnitude de deux nombres binaires pour déterminer si les deux nombres comparés sont égaux en magnitude ou si un nombre est inférieur à l'autre nombre ou supérieur à l'autre nombre.
Le comparateur peut comparer n'importe quel nombre binaire de deux n bits, où n = 1, 2, 3 et ainsi de suite.
Supposons que nous ayons deux nombres à n bits A et B, alors le comparateur à n bits recevra A et B en entrée et générera une sortie sous la forme A>B, A<B, A=B.
Le schéma fonctionnel général du comparateur à n bits est présenté dans la figure ci-dessous:

Les sections suivantes traitent du comparateur 1 bit, du comparateur 2 bits et du comparateur 3 bits.
Comparateur 1 bit
Supposons que les deux nombres binaires de 1 bit à comparer soient A et B.
A est constitué de A0 de 1 bit et B est constitué de B0 de 1 bit.
La table de vérité du comparateur 1 bit est présentée dans le tableau ci-dessous:
Les entrées sont A0 et B0.
Table de vérité du comparateur 1 bit
| Entrées Nombres binaires | Sorties | |||
| A0 | B0 | L (Inférieur à) | E (Égal à) | G (Supérieur à) |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
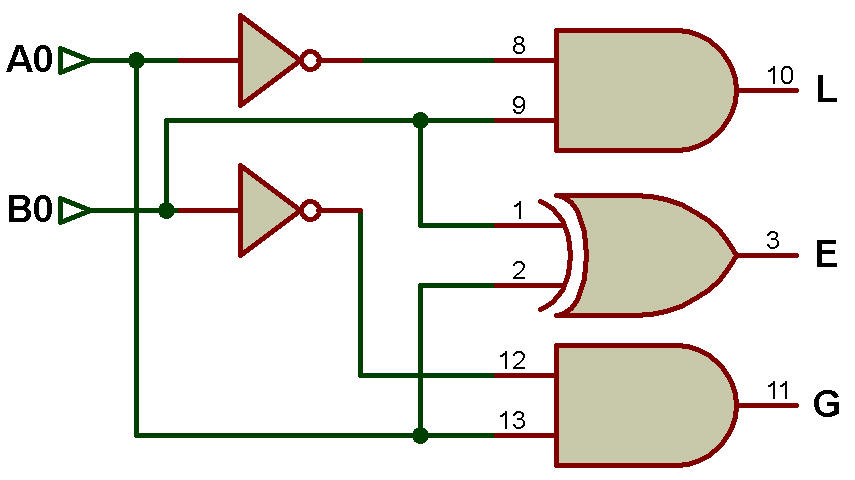
La sortie est L (inférieur à), E (égal à) et G (supérieur à).
La sortie L = 1, lorsque A0 < B0.
La sortie E = 1, quand A0 = B0.
La sortie G = 1, quand A0 > B0.
Les K-Map pour L, E et G sont présentées respectivement dans les figures ci-dessous:
| K-Map pour L | |||
| B | |||
| 0 | 1 | ||
| A | 0 | 1 | |
| 1 | |||
| K-Map pour E | |||
| B | |||
| 0 | 1 | ||
| A | 0 | 1 | |
| 1 | 1 | ||
| K-Map pour G | |||
| B | |||
| 0 | 1 | ||
| A | 0 | ||
| 1 | 1 | ||
Le schéma logique d'un comparateur 1 bit est présenté dans la figure ci-dessous:
Comparateur 2 bits
Supposons que les deux nombres binaires de 2 bits à comparer soient A et B.
A se compose de 2 bits A1A0 et B se composent de 2 bits B1B0.
La table de vérité du comparateur 2 bits est présentée dans le tableau 2.9.
Les entrées sont A1A0 et B1B0.
La sortie est L (inférieur à), E (égal à) et G (supérieur à).
La sortie L = 1, lorsque A1A0 < B1B0
La sortie E = 1 , quand A1A0 = B1B0
La sortie G= 1, quand A1A0 > B1B0
Table de vérité du comparateur 2 bit
| Valeurs Décimal | Entrées Nombres binaires | Sorties | ||||||
| A | B | A1 | A0 | B1 | B0 |
L (Inférieur à) A1A0 < B1B0 |
E (Égal à) A1A0 = B1B0 |
G (Supérieur à) A1A0 > B1B0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 2 | 2 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 3 | 3 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 4 | 4 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 5 | 5 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 6 | 6 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 7 | 7 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 8 | 8 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 9 | 9 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 10 | 10 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 11 | 11 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 12 | 12 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 13 | 13 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 14 | 14 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 15 | 15 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
Les K-Maps pour L, E et G sont présentées respectivement dans les figures ci-dessous:
K-Map pour L (A<B)
B1B0
00
01
11
10
A1A0
00
1
1
1
01
1
1
11
10
1
De K-Map,
L = A0'A1B0 + A0B0B1+A1B1
| K-Map pour E (A=B) | |||||
| B1B0 | |||||
| 00 | 01 | 11 | 10 | ||
| A1A0 | 00 | 1 | |||
| 01 | 1 | ||||
| 11 | 1 | ||||
| 10 | 1 | ||||
De K-Map,
E = A0'A1'B0'B1'+ A0A1'B0B1' + A0A1B0B1 + A0'A1B0'B1
= A0'B0'(A1' B1' + A1B1) + A0B0(A1'B1' + A1B1)
= A0'B0'(A1 XOR B1)' + A0B0(a1 XOR b1)'
= (A1 XOR B1)'[A0'B0'+A0B0]
E = (A1 XOR B1)' (A0 XOR B0)' = (A1 XNOR B1) (A0 XNOR B0)
| K-Map pour G (A>B) | |||||
| B1B0 | |||||
| 00 | 01 | 11 | 10 | ||
| A1A0 | 00 | ||||
| 01 | 1 | ||||
| 11 | 1 | 1 | 1 | ||
| 10 | 1 | 1 | |||
De K-Map,
G = A0A1B0' + A0B0'B1' + A1B1'
Comparateur 4 bits
Supposons que les deux nombres binaires de 4 bits à comparer soient A et B.
A se compose de 4 bits A3A2A1A0 et B se compose de 4 bits B3B2B1B0
Condition pour G (supérieur à), c'est-à-dire A>B :
i. Si (A3 = 1 ET B3 = 0)
OU
ii. Si (A3 = B3) et (A2 = 1 et B2 = 0 )
OU
iii. Si (A3= B3), (A2= B2) et (A= 1 et B = 0 )
OU
iv. Si (A3= B3), (A2= B2), (A1= B1) et (A0= 1 et B0= 0 )
D’après les conditions ci-dessus, la fonction booléenne pour G est :
G = A3 B3'+ (A3 XNOR B3) A2 B2'+ (A3 XNOR B3) (A2 XNOR B2) A1B1'+ (A3 XNOR B3) (A2 XNOR B2) (A1 XNOR B1) A0B0'
Condition pour E (Égal à), c'est-à-dire A=B :
i. Si (A3= B3), (A2= B2), (A1= B1) et (A0 = B0)
D'après la condition ci-dessus, la fonction booléenne pour E est :
E = (A3 XNOR B3) (A2 XNOR B2) (A1 XNOR B1) (A0 XNOR B0)
Condition pour L (supérieur à), c'est-à-dire A<B :
i. Si (A3 = 0 et B3 = 1)
OU
ii. Si (A3 = B3) et (A2 = 0 et B2 = 1)
OU
iii. Si (A3 = B3), (A2 = B2) et (A1 = 0 et B1 = 1)
OU
iv. Si (A3 = B3), (A2 = B2), (A1 = B1) et (A0 = 0 et B0 = 1)
D'après les conditions ci-dessus, la fonction booléenne pour L est :
L = A3' B3+ (A3 XNOR B3) A2'B2+ (A3 XNOR B3) (A2 XNOR B2) A1'B1 + (A3 XNOR B3) (A2 XNOR B22) (A1 XNOR B1) A0' B0
