Compteur MOD-N
Voici différents circuits intégrés de conteurs
| 4026BE | 7 segment dysplay decade counter |
| 4510BE | Presettable BCD up/down Counter |
| 4017BE | Decade counter |
| 4520 | Double compteur binaire |
| 74HC191 | Presettable Binary Up/Down Counter |
| 4029BCN | Presettable Binary/Decade Up/Down Counter |
| 14029BCP | Presettable Binary/Decade Up/Down Counter |
| 74HC193 | 4-Bit Synchronous Up/Down Counters (Dual Clock With Clear). |
| 74LS469NS | 8-Bit Binary Up-Down Counter |
| 74LS 592N | 8 Bit binary counters with intput registers |
| 74LS90 | Divide-by-12 counter decade counter and 4-Bit binary counter |
| 74LS 92N | Divide-by-12 counter decade counter |
| 74HC393 | Double compteur binaire |
| 4020 | 14-Stage Ripple Carry Binary Counters |
| 4040 | 12-Stage Ripple Carry Binary Counters |
| 74HC4060 | 14-stages binary ripple counter with oscillator |
| 4060 | 14-stages binary ripple counter with oscillator |
| 4521 | 24-stages frequency divider |
Le MOD-N-COUNTER est le compteur qui suit le module d'un compteur.
Le module d'un compteur est le nombre d'états logiques uniques qu'un compteur traverse avant de revenir à son état initial et de commencer à répéter la séquence.
Par exemple, un compteur « n » bits a un module de 2n, où « n » est le nombre de bascules dans le compteur.
Le module d'un compteur peut être défini à la fois pour un compteur asynchrone et synchrone.
Le compte 2n est le décompte naturel.
Cela signifie que le compteur 'n' bits compte (parcourt) tous ses états naturels sans sauter aucun état et a donc des modules de 2n.
Nous avons donc :
Avec n= 1, le compteur à bascule aura un module de 21=2 et les états sont 0, 1.
Avec n = 2, le compteur à bascule aura un module de 22=4 et les états sont 00, 01, 10,11.
Avec n = 3, 23=8, 000, 001,...,110, 111.
Avec n = 4, 24=16, 0000, 0001,...,1110, 1111.
Ainsi nous avons trouvé que le module de 2n est une puissance de 2.
Supposons maintenant que si nous voulons un module inférieur à 2n, alors le compteur est modifié pour ignorer certains états afin d'obtenir un module inférieur à 2n.
Par exemple, le compteur MOD-10 (compteur décimal) vu dans la section précédente, on a n=4, et peut compter 2n=24= 16 états mais 6 états sont ignorés pour obtenir le compteur mod-10.
Le mod-10 le compteur compte donc 0000, 0001,..., 1000, 1001 uniquement.
Discutons de quelques autres compteurs MOD.
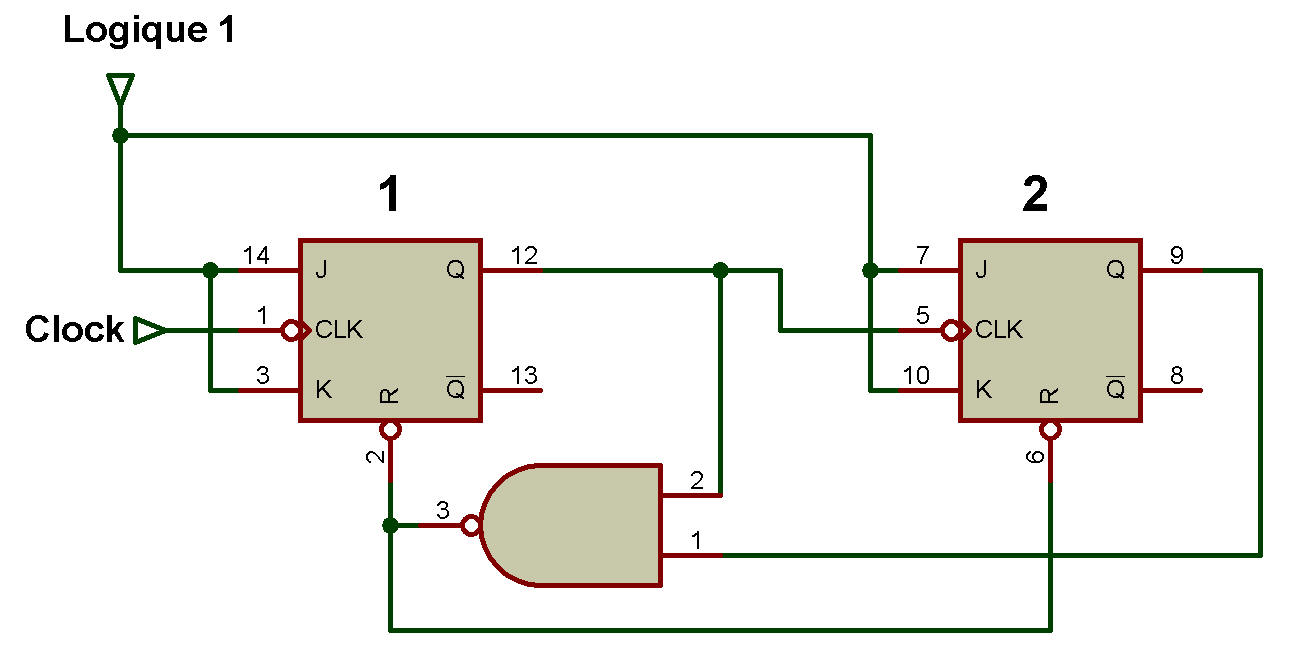
Compteur MOD-3
La figure ci-dessous montre le compteur MOD-3 (déclanchement à front négatif).

La table d'état est présentée dans le tableau ci-dessous:
| C (clk) | Q2 | Q1 | Description |
| 0 | 0 | 0 | État initial |
| 1 | 0 | 1 | Seul Q1 change |
| 2 | 1 | 0 | Q1 et Q2 changements |
| 3 | 0 | 0 | Retour à l'état initial |
Le chronogramme est présenté à la figure ci-dessous:
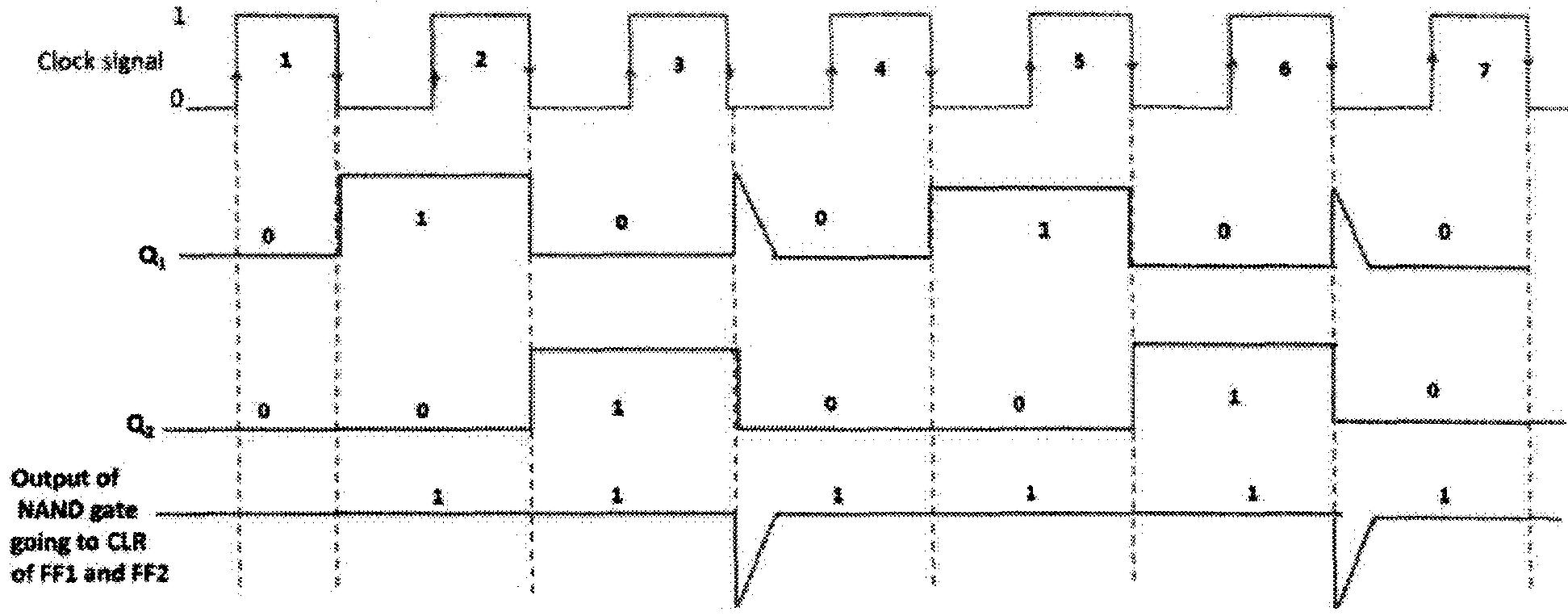
Les entrées de la porte NAND 1 sont Q1 et Q2 et la sortie de la porte NAND 1 va à l'entrée d'effacement (R) de la bascule 1 et de la bascule 2.
Compteur MOD-5
La figure ci-dessous montre le compteur MOD-5 (déclanchement à front négatif).
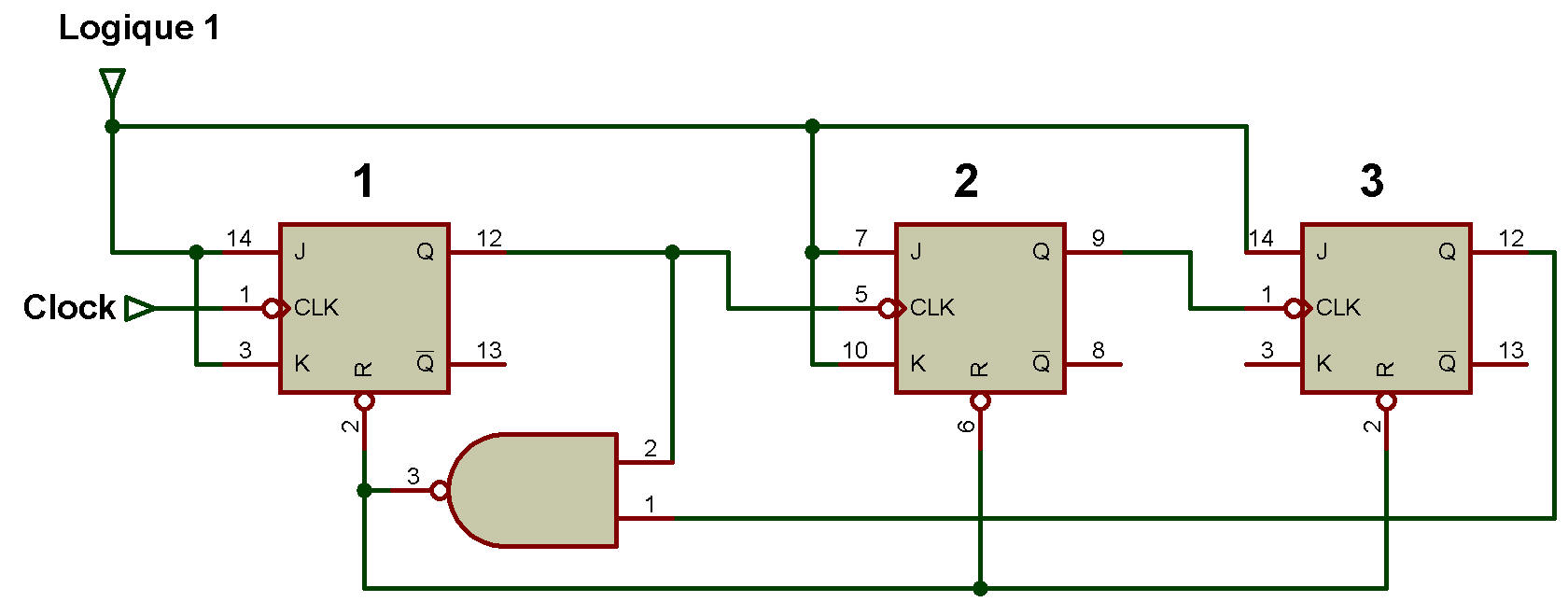
La table d'état est présentée dans le tableau ci-dessous:
| C (clk) | Q3 | Q2 | Q1 | Description |
| 0 | 0 | 0 | 0 | État initial |
| 1 | 0 | 0 | 1 | Seul Q1 change |
| 2 | 0 | 1 | 0 | Q1 et Q2 changements |
| 3 | 0 | 1 | 1 | Seul Q1 change |
| 4 | 1 | 0 | 0 | Q1, Q2 et Q3 changements |
| 5 | 1 | 0 | 1 | Seul Q1 change |
| 6 | 0 | 0 | 0 | Retour à l'état initial |
Compteur MOD-6
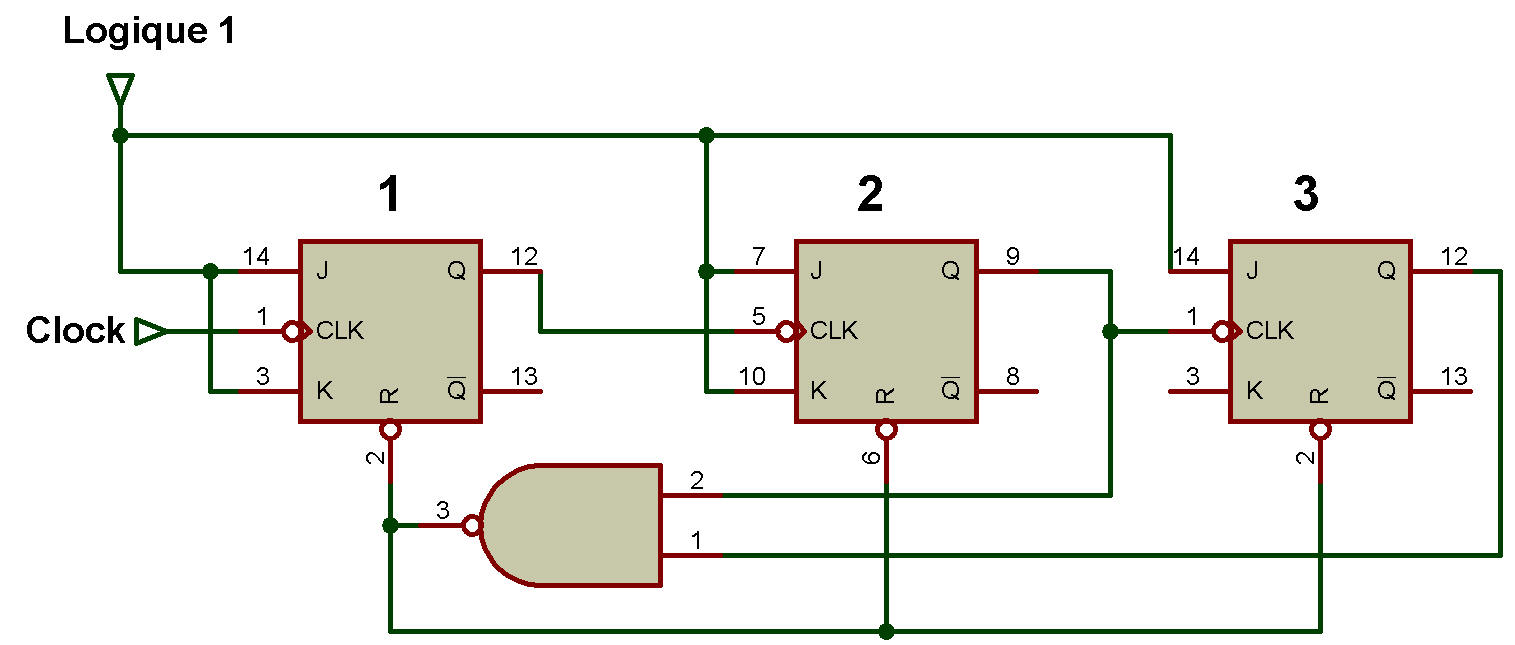
La table d'état est présentée dans le tableau ci-dessous:
| C (clk) | Q3 | Q2 | Q1 | Description |
| 0 | 0 | 0 | 0 | État initial |
| 1 | 0 | 0 | 1 | Seul Q1 change |
| 2 | 0 | 1 | 0 | Q1 et Q2 changements |
| 3 | 0 | 1 | 1 | Seul Q1 change |
| 4 | 1 | 0 | 0 | Q1, Q2 et Q3 changements |
| 5 | 1 | 0 | 1 | Seul Q1 change |
| 6 | 1 | 1 | 0 | Q1 et Q2 changements |
| 7 | 0 | 0 | 0 | Retour à l'état initial |
