Démultiplexeurs (DMUX)
DMUX est un circuit combinatoire qui agit à l'opposé de celui du multiplexeur (MUX). Un DMUX reçoit l’entrée d’une seule ligne d’entrée et possède de nombreuses lignes de sortie.
En général, DMUX a 1 ligne d'entrée et 2 lignes de sortie. Les lignes de sélection 'n' décident laquelle des lignes de sortie 2n recevra la sortie.
Si nous désignons les données sur la ligne d'entrée du DMUX par Di (entrée de données), alors ces données Di apparaîtront telles quelles sur l'une des lignes de sortie 2n sélectionnées par la ligne de sélection 'S'.
Si Di = 1, alors la ligne de sortie sélectionnée par la ligne de sélection 'S' obtiendra la sortie 1.
Si Di = 0, alors la ligne de sortie sélectionnée par la ligne de sélection 'S' obtiendra la sortie 0.
Les sections à venir traiteront de divers DMUX - 1:2 DMUX, 1:4 DMUX, 1:8 DMUX, etc.
Avant de discuter du DMUX en détail, voyons divers circuits intégrés DMUX disponibles répertoriés dans le tableau ci-dessous:
| Ic | Description |
| 74138 | 3 to 8 Demux |
| 74139 | Dual 1:4 Demux |
| 74154 | 1:16 Demux |
DMUX 1:2
La table de vérité du DMUX 1:2 est présentée dans le tableau ci-dessous:
| Enable | Select | Entrées | Sorties | ||
| E | S | Di | D1 | D0 | |
| 0 | x | x | x | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 2 | 1 | 0 | 0 | 0 |
| 1 | 3 | 1 | 1 | 1 | 0 |
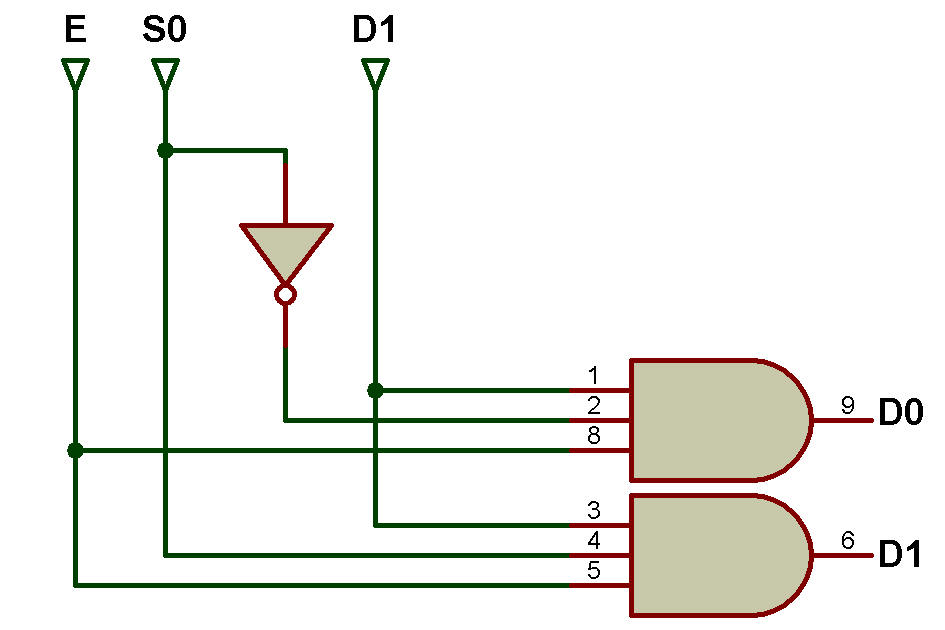
DMUX a une ligne d'entrée Di, une ligne de sélection S et deux lignes de sortie D0 et D1
A partir de la table de vérité, lorsque E = 1 et S= 0, alors la sortie D0 est sélectionnée.
Donc si Di = 0, alors D0 = 0 et si Di = 1, alors D0 = 1.
De même, lorsque E = 1 et S = 1 alors la sortie D1 est sélectionnée.
Donc si Di = 0, alors D1 = 0 et si Di = 1, puis D1 = 1.
Le diagramme logique est présenté à la figure ci-dessous:

La carte K pour D0 et D1 est illustrée dans la figure ci-dessou:
| D0 = S'Di | D1 = SDi | |||
| Di | ||||
| S | 0 | 1 | 0 | 1 |
| 0 | 1 | |||
| 1 | 1 | |||
1:4 DMUX
Le schéma fonctionnel du DMUX 1:4 est présenté dans la figure ci-dessous:
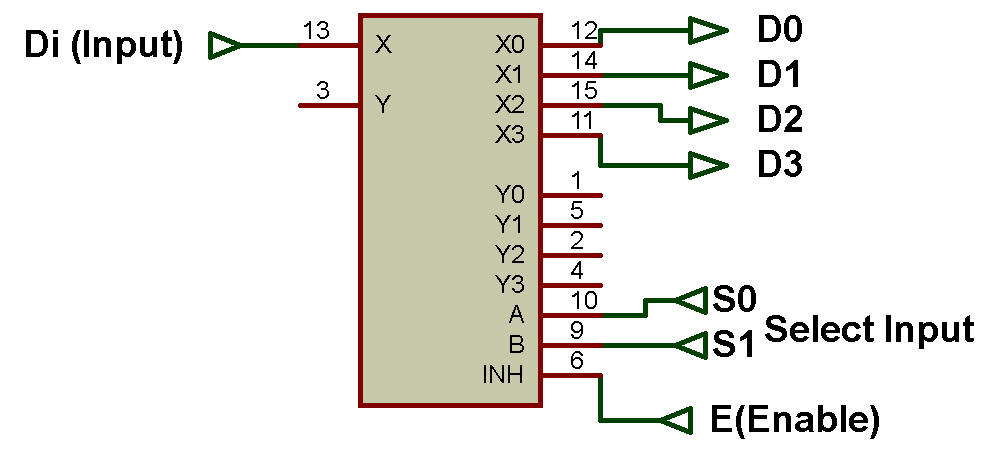
La table de vérité du DMUX 1:4 est présentée dans le tableau ci-dessous:
| Enable | Select | Entrées | Sorties | |||||
| E | S1 | S0 | Di | D3 | D2 | D1 | D0 | |
| 0 | x | x | x | x | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Di |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | Di |
| 1 | 2 | 0 | 1 | 0 | 0 | 0 | Di | 0 |
| 1 | 3 | 0 | 1 | 1 | 0 | 0 | Di | 0 |
| 1 | 4 | 1 | 0 | 0 | 0 | Di | 0 | 0 |
| 1 | 5 | 1 | 0 | 1 | 0 | Di | 0 | 0 |
| 1 | 6 | 1 | 1 | 0 | Di | 0 | 0 | 0 |
| 1 | 7 | 1 | 1 | 1 | Di | 0 | 0 | 0 |
DMUX a une ligne d'entrée Di deux lignes de sélection S0 et S1 et quatre lignes de sortie D0, D1, D2, D3.
Les K-Maps pour D0, D1, D2, D3 sont présentées respectivement dans le figures ci-dessous:
| D0 = S0'S1'Di | D1 = S0S1'Di | D2 = S0'S1Di | D3 = S0S1Di | |||||
| Di | ||||||||
| S | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 00 | 1 | |||||||
| 01 | 1 | |||||||
| 11 | ||||||||
| 10 | 1 | 1 | ||||||
Le schéma logique est présenté dans la figure ci-dessous:
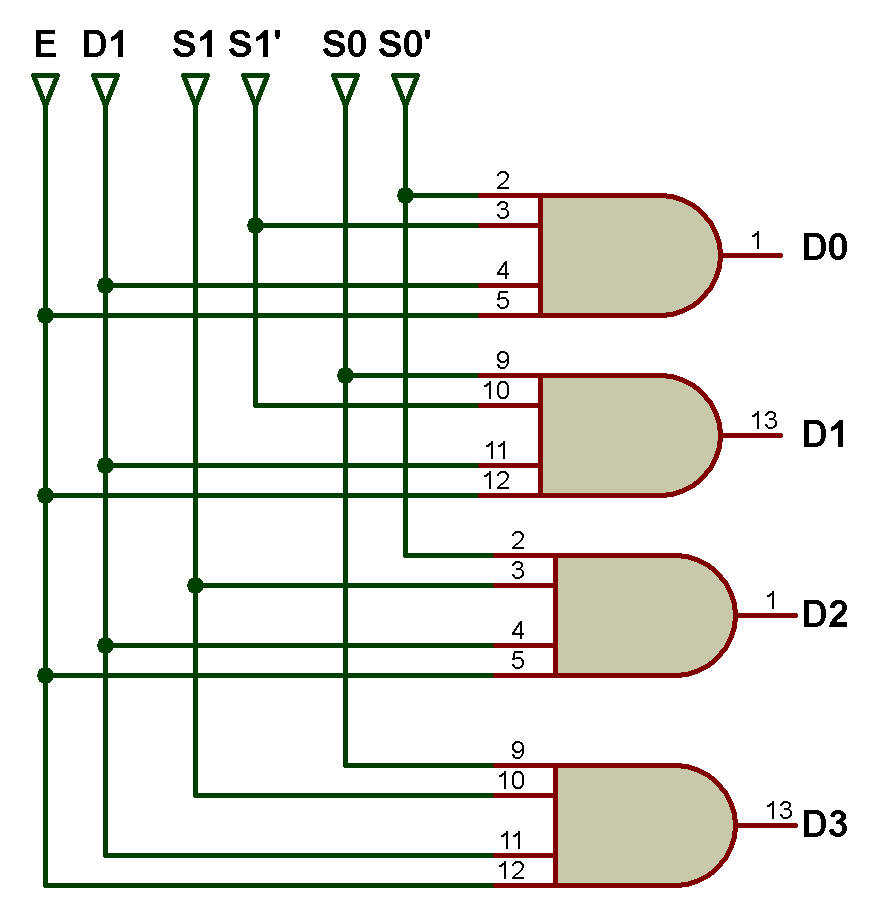
1:8 DMUX
Le schéma logique de 1:8 DEMUX est présenté dans la figure ci-dessous:
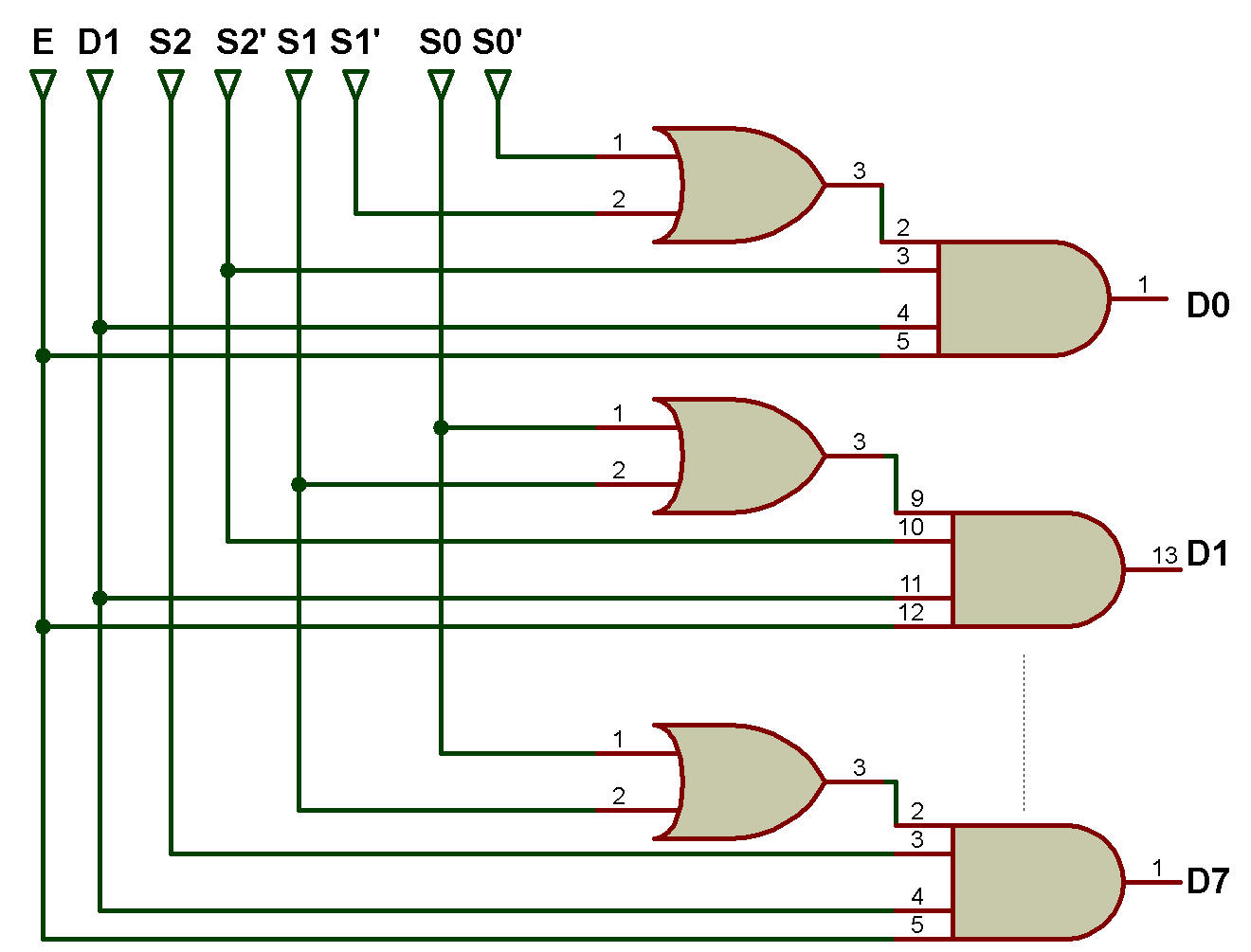
D0 = DiS2'S1'S0' D1 = DiS2'S1'S0
D2 = DiS2'S1S0' D3 = DiS2'S1S0
D4 = DiS2S1'S0' D5 = DiS2'S1S0'
D6 = DiS2'S1'S0 D7 = DiS2S1S0
La table de vérité de 1 DEMUX est présentée dans le tableau ci-dessous:
| Enable | Select | Entrées | Sorties | ||||||||||
| E | S2 | S1 | S0 | Di | D7 | D6 | D5 | D4 | D3 | D2 | D1 | D0 | |
| 0 | x | x | x | x | x | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Di |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Di |
| 1 | 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Di | 0 |
| 1 | 3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | Di | 0 |
| 1 | 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Di | 0 | 0 |
| 1 | 5 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | Di | 0 | 0 |
| 1 | 6 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | Di | 0 | 0 | 0 |
| 1 | 7 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | Di | 0 | 0 | 0 |
| 1 | 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | Di | 0 | 0 | 0 | 0 |
| 1 | 9 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | Di | 0 | 0 | 0 | 0 |
| 1 | 10 | 1 | 0 | 1 | 0 | 0 | 0 | Di | 0 | 0 | 0 | 0 | 0 |
| 1 | 11 | 1 | 0 | 1 | 1 | 0 | 0 | Di | 0 | 0 | 0 | 0 | 0 |
| 1 | 12 | 1 | 1 | 0 | 0 | 0 | Di | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 13 | 1 | 1 | 0 | 1 | 0 | Di | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 14 | 1 | 1 | 1 | 0 | Di | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 15 | 1 | 1 | 1 | 1 | Di | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Le DMUX a une ligne d'entrée Di, trois lignes de sélection S0, S1 et S2 et huit lignes de sortie D0, D1, D2, D3, D4, D5, D6, et D7
DMUX en cascade
Deux DMUX ou plus peuvent être mis en cascade pour former un DMUX plus grand.
Exemple : Concevoir un DMUX 1:16 en utilisant deux DMUX 1:8.
Solution : 1:16 DMUX utilisant deux DMUX 1:8 est illustré dans la figure ci-dessous:
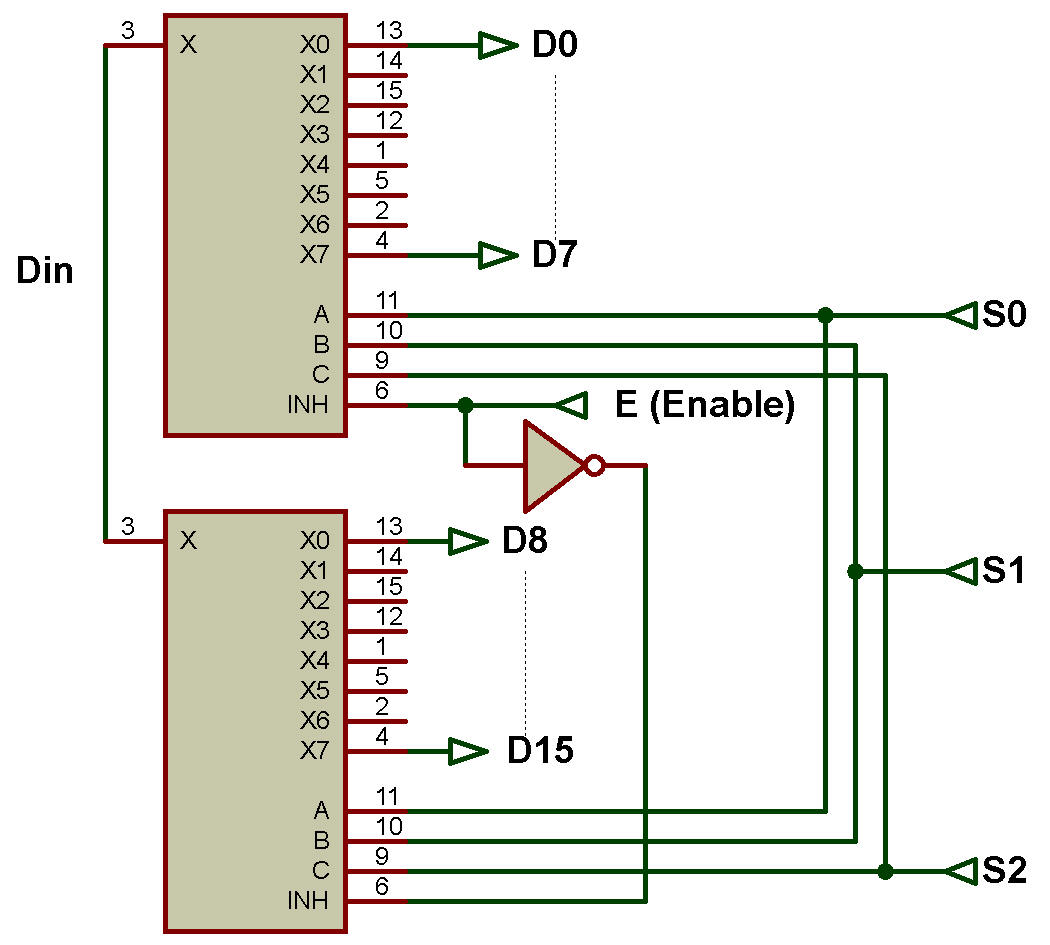
Implémentation d'un circuit combinatoire et d'une fonction booléenne à l'aide de DMUX
Exemple: implémenter un additionneur complet à l'aide de DMUX.
Solution : La table de vérité de l'additionneur complet utilisant DMUX est présentée dans le tableau ci-dessous.
Les sorties sont S (Sum) et C (Carry). Les entrées sont X, Y, Z (Z est le report d'entrée).
Table de vérité de l'additionneur complet
| Entrées | Sorties | |||
| X | Y | Z | S | C |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
L'implémentation de l'additionneur complet utilisant DMUX est illustrée à la figure ci-dessous.
Les portes OR sont utilisées pour combiner les sorties.
S(X, Y, Z) = Σm(1, 2, 4, 7) et C(X, Y, Z) = Σm(3, 5, 6, 7)
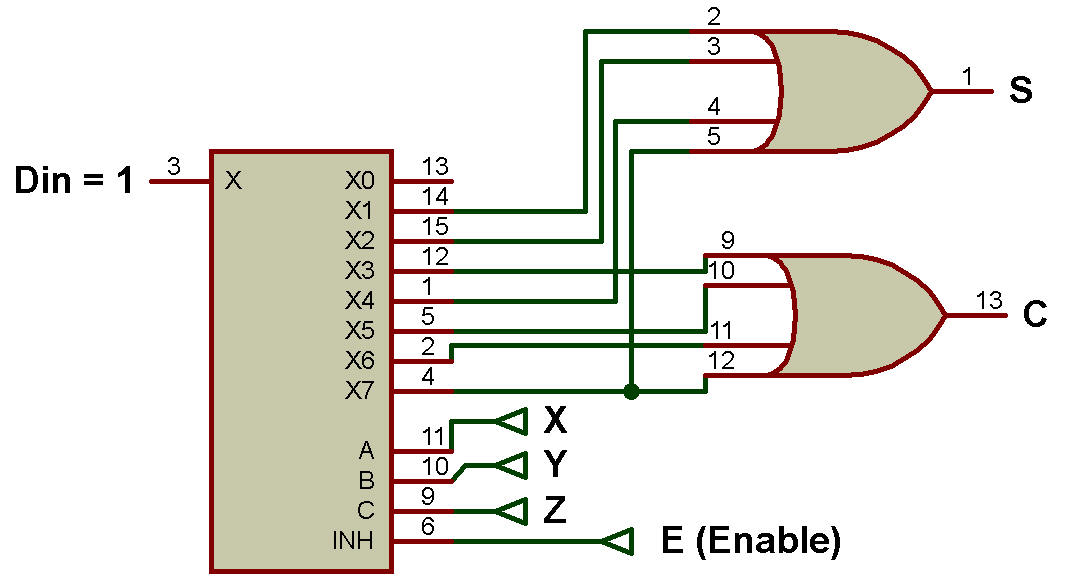
Exemple 10 : Implémentez la fonction booléenne « F » à l'aide de DMUX.
F(X,Y,Z) = Σ(0,2,6,7)
Solution :
Puisque la fonction booléenne F a trois variables donnant un total de 23 sorties, donc un 1:8 DMUX est utilisé.
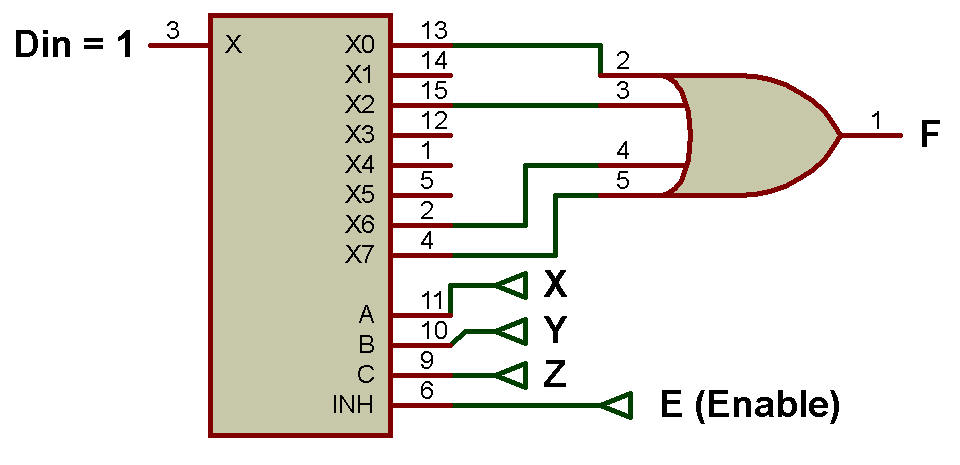
Applications des DMUX
I. Utilisé pour implémenter des circuits logiques combinatoires et des fonctions booléennes.
ii. Transmission de données.
