Encodeurs
Les encodeurs sont des circuits combinatoires qui acceptent les entrées binaires et génèrent des sorties binaires en fonction de celles de leurs entrées activées.
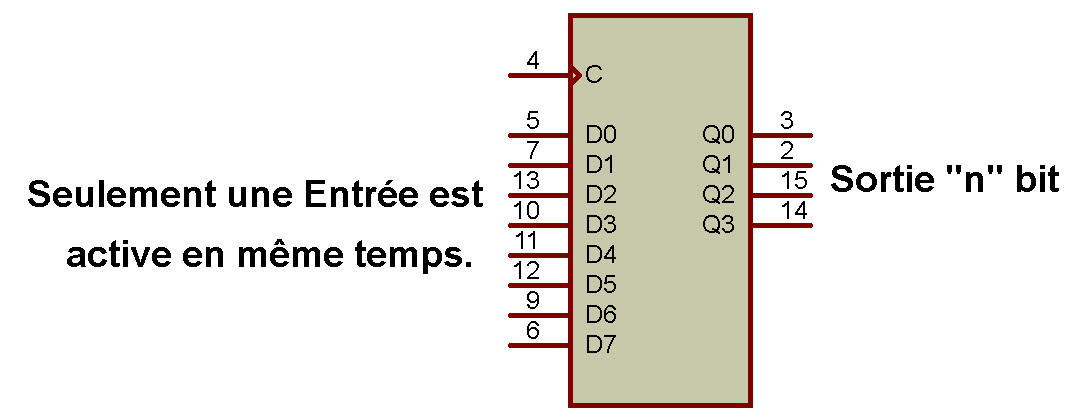
L'encodeur a des entrées de 2n (ou peut être inférieure à 2n) et génère «n» sorties.
La structure générale de 2n : n d'un circuit codeur est illustré à la figure ci-dessous:

Comme le montre la figure, il y a des entrées de 2n (ou peut être inférieure à 2n).
Sortie de 2n, une seule entrée est activée à la fois, c'est-à-dire qu'une seule entrée est au « 1 » logique.
En fonction de l'entrée qui est au « 1 » logique, le code de sortie correspondant est généré.
Certains encodeurs courants sont :
Encodeur octal vers binaire (8 lignes d'entrée et 3 lignes de sortie),
Encodeur décimal vers BCD (10 lignes d'entrée et 4 lignes de sortie),
Encodeur octal vers binaire (16 lignes d'entrée et 4 lignes de sortie), etc.
Dans les sections à venir, nous discuterons de l'encodeur octal vers binaire, de l'encodeur décimal vers BCD et des encodeurs prioritaires.
Encodeur octal vers binaire
L'encodeur octal à binaire dispose de 8 lignes d'entrée, une pour chaque chiffre octal, et de 3 lignes de sortie qui génèrent le code binaire en fonction de celle de la sortie de ligne d'entrée de 8 lignes d'entrée qui est activée.
La table de vérité pour l'encodeur octal à binaire est présentée dans le tableau ci-dessous:
| Table de vérité pour l'encodeur octal vers binaire | |||||||||||
| Entrées | Sorties | ||||||||||
| Chiffres | I7 | I6 | I5 | I4 | I3 | I2 | I1 | I0 | B2 | B1 | B0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
D'après le tableau, il est clair que lorsque l'entrée I0 = 1, alors la sortie générée est B2B1B0 = 0 0 0.
Ici, une chose à noter est que si toutes les entrées I0 à I7 sont « 0 », alors la sortie générée est également B2B1B0 = 0 0 0.
Il s'agit d'une ambigüité car la sortie générée dans les deux cas est la même.
Ce problème peut être résolu en fournissant une ligne de sortie supplémentaire, par exemple « Y ».
Ce « Y » spécifie qu'aucune des entrées (I0 à I7) n'est « 1 » et donc la sortie « Y » = « 1 ».
Le schéma logique de l'encodeur octal vers binaire est présenté dans la figure ci-dessous:
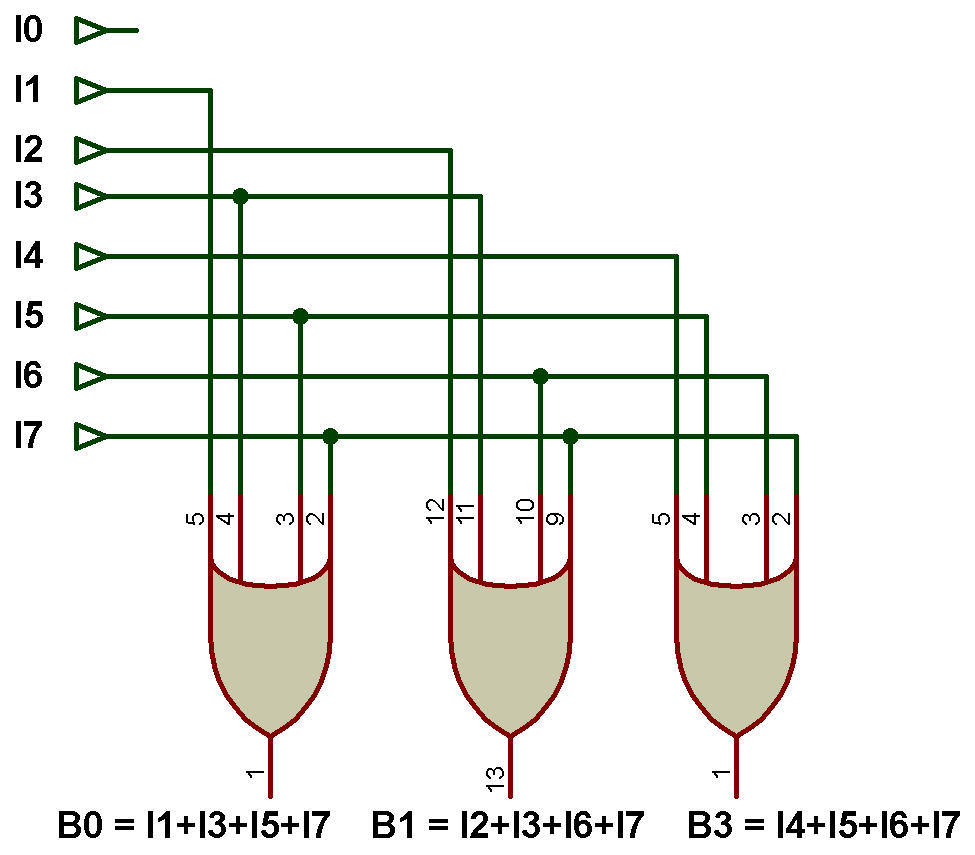
Sortie,
B0 = I1 + I3 + I5 + I7
B1 = I2 + I3 + I6 + I7
B2 = I4 + I5 + I6 + I7
I0 n'est présent dans aucune des sorties, donc I0 agit comme si on s'en fichait.
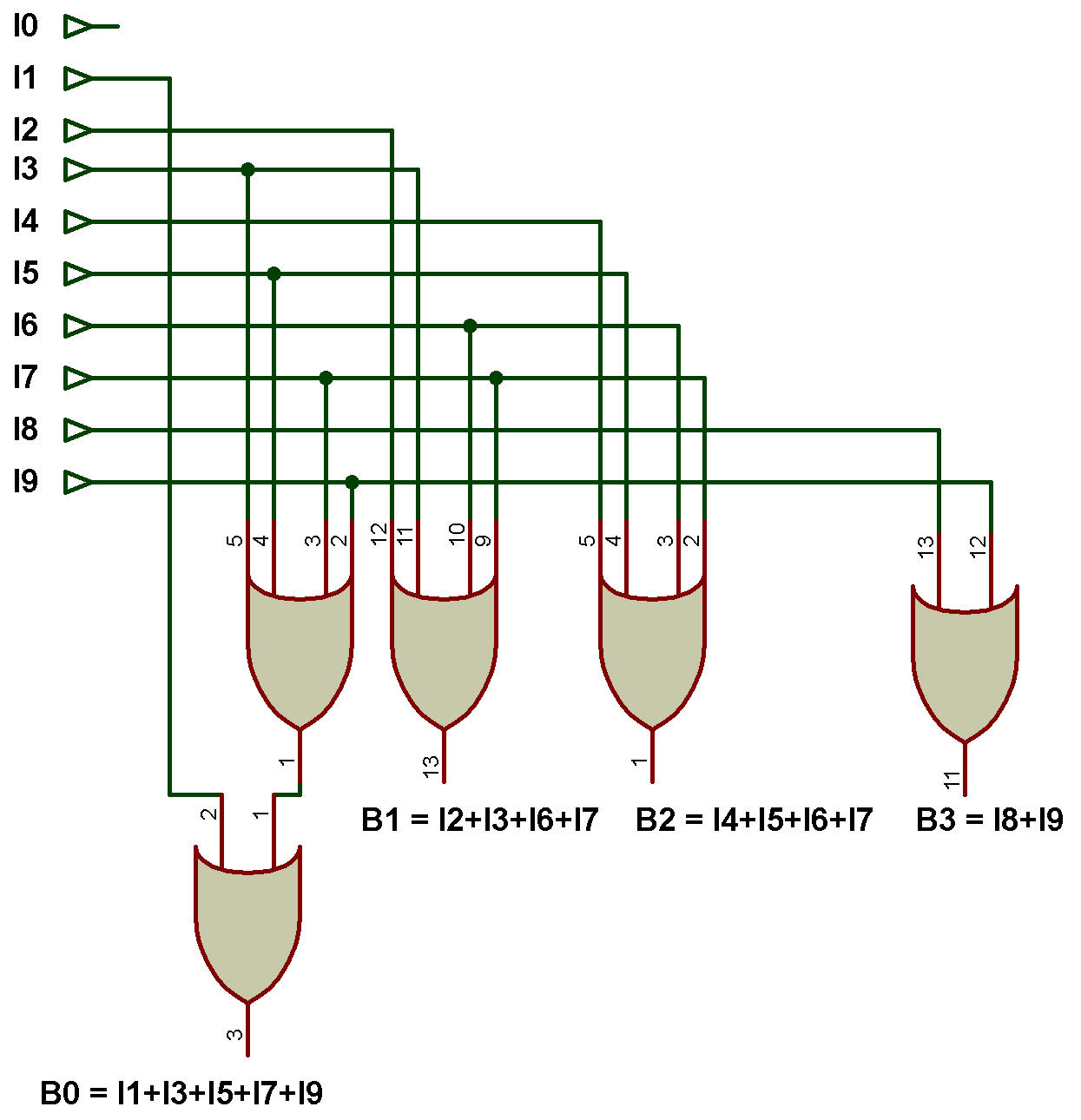
Encodeur décimal vers BCD
L'encodeur octal vers binaire dispose de 10 lignes d'entrée, une pour chaque chiffre décimal et de 4 lignes de sortie qui génèrent le code BCD en fonction de laquelle des 10 lignes d'entrée est activée.
La table de vérité pour l'encodeur décimal vers BCD est présentée dans le tableau ci-dessous:
| Table de vérité pour l'encodeur BCD vers binaire | ||||||||||||||
| Entrées | Sorties | |||||||||||||
| Chiffres | I9 | I8 | I7 | I6 | I5 | I4 | I3 | I2 | I1 | I0 | B3 | B2 | B1 | B0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 6 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 7 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 8 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Sortie,
B0 = I1 + I3 + I5 + I7+ I9
B1 = I2 + I3 + I6 + I7
B2 = I4 +I5 + I6 + I7
B3 = I8 + I9
Le schéma fonctionnel de l'encodeur décimal vers BCD est illustré dans la figure ci-dessous:
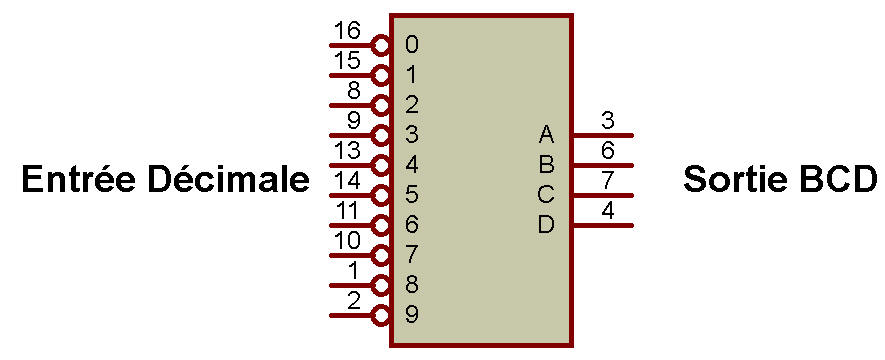
Le schéma logique de l'encodeur décimal vers BCD est illustré dans la figure ci-dessous:
Encodeur prioritaire
L'encodeur discuté jusqu'à présent n'a qu'une seule entrée active à la fois. Supposons que si dans un circuit deux entrées ou plus sont actives (en logique 1) en même temps, alors cette condition est gérée par l'encodeur prioritaire.
L'encodeur de priorité a une fonction de priorité qui décide de la priorité de toutes les entrées activées (en logique 1) à un moment donné.
Parmi toutes les entrées activées, celle ayant la priorité la plus élevée sera prise en compte et la sortie sera générée en fonction de l'entrée la plus prioritaire.
Par exemple, si nous appuyons sur la touche du clavier (5)10 = 0101 puis appuyons sur la touche du clavier (9)10 = 1001, avant de relâcher la touche 5, alors 9 et 5 sont activés (à logique 1).
En fonction du système de priorité, les priorités des entrées sont définies.
Supposons que dans l'exemple ci-dessus la priorité soit définie sur l'ampleur relative, alors 9>5 et 9 bénéficie d'une priorité plus élevée que 5.
Par conséquent, la sortie sera générée en fonction de l'entrée 9.
L'encodeur prioritaire à 4 entrées est décrit ci-dessous.
Encodeur de priorité à 4 entrées
La table de vérité pour le codeur prioritaire à 4 entrées est présentée dans le tableau ci-dessous:
| Table de vérité pour l'encodeur prioritaire à 4 entrées | ||||||
| Entrées | Sorties | |||||
| I3 | I2 | I1 | I0 | A | B | V |
| 0 | 0 | 0 | 0 | x | x | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | x | 0 | 1 | 1 |
| 0 | 1 | x | x | 1 | 0 | 1 |
| 1 | x | x | x | 1 | 1 | 1 |
Comme le montre le tableau, nous avons 4 entrées - I0 I1 I2 I3
Les sorties sont désignées par A, B et V. La sortie V=l, lorsqu'une ou plusieurs des entrées sont égales à 1.
Si toutes les entrées sont égaux à zéro, alors V= 0.
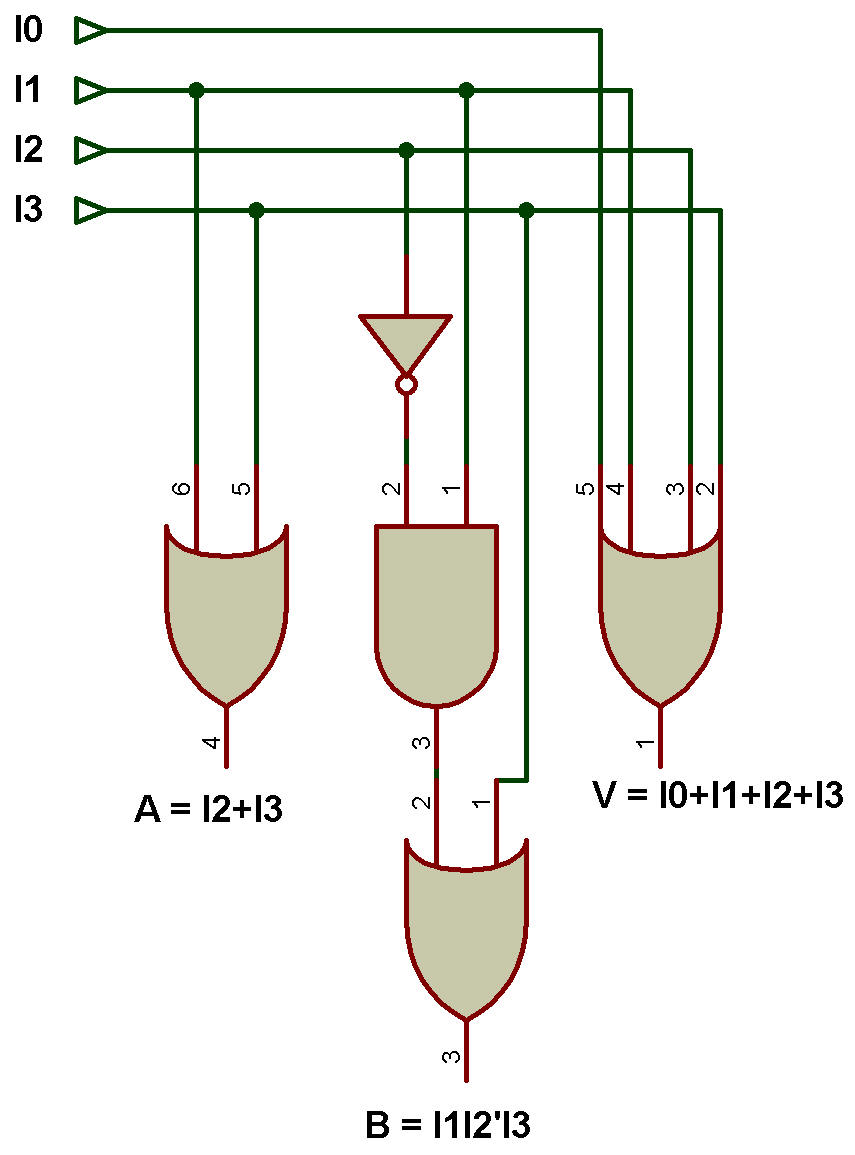
L'entrée I3 a la priorité la plus élevée. Cela signifie que si I3 = 1, alors la sortie AB = 11, quelles que soient les valeurs d'entrée des autres entrées I2, I1 et I0.
L'entrée I2 a la deuxième priorité la plus élevée. Cela signifie que si I2 = 1 et que l'entrée de priorité la plus élevée I3 est égale à 0, alors la sortie AB = 10, quelles que soient les valeurs d'entrée des autres entrées I1 et I0.
L'entrée I1 a la priorité immédiatement supérieure. Cela signifie que si I1 = 1 et que toutes les entrées de priorité supérieure à I1 sont égales à « 0 », alors la sortie AB = 01, quelle que soit la valeur d'entrée de l'entrée I0.
L'entrée I0 à la moindre priorité. Cela signifie que si I0 = 1 et que toutes les entrées avec une priorité supérieure à I0 sont égales à « 0 », alors la sortie AB = 00.
La table de vérité du tableau ci-haut montre seulement une combinaison de 5 valeurs d'entrée.
Lorsque (Ne s'en soucie pas) sont remplacés par '0' puis par '1', alors nous obtenons 16 combinaisons d'entrée.
La table de vérité complète est présentée dans le tableau ci-dessous:
| Table de vérité complète pour l'encodeur prioritaire à 4 entrées | ||||||
| Entrées | Sorties | |||||
| I3 | I2 | I1 | I0 | A | B | V |
| 0 | 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| Remplacer par '0' < puis par '1' | ||||||
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| Remplacer par '0' < puis par '1' | ||||||
| 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| Remplacer par '0' < puis par '1' | ||||||
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
La K-Map pour A, B et V est représentée respectivement dans les figures ci-dessous:
| K-Map pour A | |||||
| I2I3 | |||||
| 00 | 01 | 11 | 10 | ||
| I0I1 | 00 | x | 1 | 1 | 1 |
| 01 | 1 | 1 | 1 | ||
| 11 | 1 | 1 | 1 | ||
| 10 | 1 | 1 | 1 | ||
De K-Map, A = I2 + I3
| K-Map pour B | |||||
| I2I3 | |||||
| 00 | 01 | 11 | 10 | ||
| I0I1 | 00 | x | 1 | 1 | |
| 01 | 1 | 1 | 1 | ||
| 11 | 1 | 1 | 1 | ||
| 10 | 1 | 1 | |||
De K-Map, B = I1I2'+ I3
| K-Map pour V | |||||
| I2I3 | |||||
| 00 | 01 | 11 | 10 | ||
| I0I1 | 00 | 0 | 1 | 1 | 1 |
| 01 | 1 | 1 | 1 | 1 | |
| 11 | 1 | 1 | 1 | 1 | |
| 10 | 1 | 1 | 1 | 1 | |
De K-Map, V = I0 + I1 + I2+ I3
Le schéma logique du codeur prioritaire à 4 entrées est présenté dans la figure ci-dessous: