Implémentation d'une fonction logique à l'aide de portes
Introduction : Dans cette section, nous discuterons de l'implémentation de fonctions logiques (fonctions booléennes) utilisant diverses portes.
Cette section couvrira les sujets suivants :
i. Implémentation à deux niveaux (implémentation de fonctions logiques utilisant des portes NAND-NOR) de fonctions logiques (booléennes)
ii. Autres implémentations à deux niveaux de fonctions logiques
iii. Formes non dégénérées et formes dégénérées
1. Implémentation à deux niveaux de la fonction logique (booléenne) :
Introduction : Par niveau de portes, nous entendons le nombre maximum de portes connectées en série entre l'entrée et la sortie pour obtenir le réseau logique (circuit) requis.
A noter également que INVERTER (NOT) n'est pas pris en compte lorsqu'un niveau de porte est décidé dans un réseau logique.
Ainsi, une implémentation à deux niveaux signifie qu'une fonction logique (booléenne) est implémentée de telle sorte que chacune des entrées ne doit en passer que par deux pour obtenir la sortie souhaitée.
Une fonction booléenne donnée, sous forme SOP ou POS, peut être implémentée en utilisant une logique de porte à deux niveaux.
L'implémentation à deux niveaux peut être effectuée en utilisant des portes AND et OR ou en utilisant soit la porte NAND uniquement, soit la porte NOR uniquement.
Voir NON-ET Une porte Universelle, NON-OU Une porte Universelle
Les fonctions logiques, lorsqu'elles sont mises en œuvre pratiquement à l'aide de circuits et de réseaux numériques, sont principalement construites à l'aide de portes NAND ou NOR.
En effet, les portes NAND et NOR sont des portes universelles, souvent appelées blocs de construction universels, car tout type de portes ou fonctions logiques peut être implémenté à l'aide de ces portes.
De plus, les portes NAND et NOR sont plus faciles à fabriquer avec des composants électroniques et constituent les portes de base utilisées dans toutes les familles logiques numériques IC (circuit intégré).
En raison de la facilité d'utilisation des portes NAND et NOR, la conception est réalisée de manière à ce que, étant donné la fonction booléenne exprimée à l'aide de AND, OR et NOT, puisse être également exprimée à l'aide de portes NAND ou NOR.
Maintenant, afin d'utiliser les portes NAND et NOR pour diverses implémentations de fonctions logiques, nous allons examiner deux autres symboles graphiques pour les portes NAND et NOR.
Les deux symboles de la porte NAND sont représentés sur les figures ci-dessous:
| Figure a | Figure b |
Porte NAND
utilisant AND-NOT |
Porte NAND utilisant NOT-OR |
Comme le montre la figure (a), le symbole AND-NOT est simplement identique à la porte NAND.
La figure (b) est NOT-OR où la porte NON-ET est représentée par une porte OU avec de petits cercles en entrée pour inverser l'I/P à venir.
La sortie générée est:
a '+ b' + c', qui est égal à (a. b. c)' —> en utilisant la loi de De-Morgan
De même, les deux symboles pour la porte NOR sont représentés sur les figures ci-dessous:
| Figure a | Figure b |
Porte NOR utilisant OR-NOT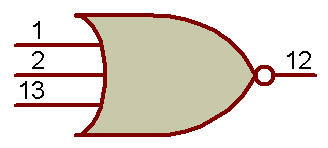 |
Porte NOR utilisant NOT-AND |
Comme le montre la figure (a), le symbole OR-NOT est simplement le même que la porte NOR.
La figure (b) est NOT-AND où la porte NOR est représentée par la porte ET avec de petits cercles en entrée pour inverser l'entrée entrante.
La sortie générée est :
a'. b'. c', qui est égal à (a + b + c)' [en utilisant la loi de De-Morgan]
Il convient également de noter que toute porte NAND ou NOR avec une seule entrée se comporte comme un NOT, comme le montrent les figures ci-dessous:
NOT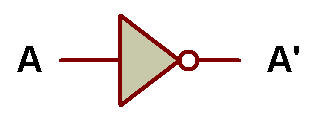 |
NOT
en utilisant la porte NAND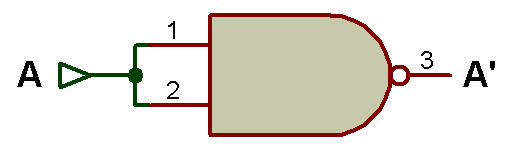 |
NOT en utilisant la porte NOR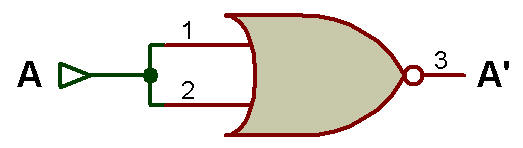 |
Comme nous avons discuté de divers symboles de portes NAND et NOR, nous allons maintenant discuter de l'implémentation de la fonction booléenne à l'aide de la porte NAND et de l'implémentation de la fonction booléenne à l'aide de la porte NOR.
Implémentation de la fonction booléenne à l'aide de la porte NAND
Afin d'implémenter la fonction booléenne à l'aide de portes NAND, la condition est que la fonction booléenne soit sous la forme SOP (Sum of Product).
Prenons quelques exemples d'implémentation d'une fonction booléenne à l'aide de la porte NAND.
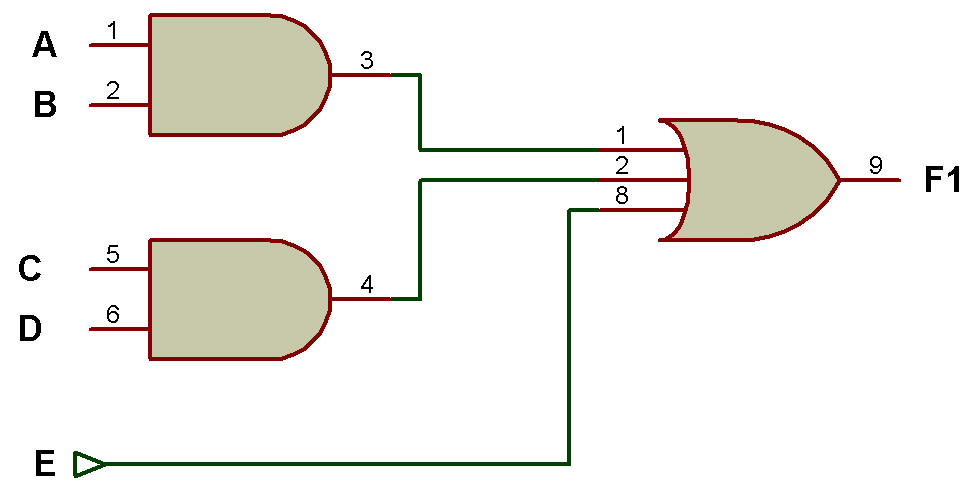
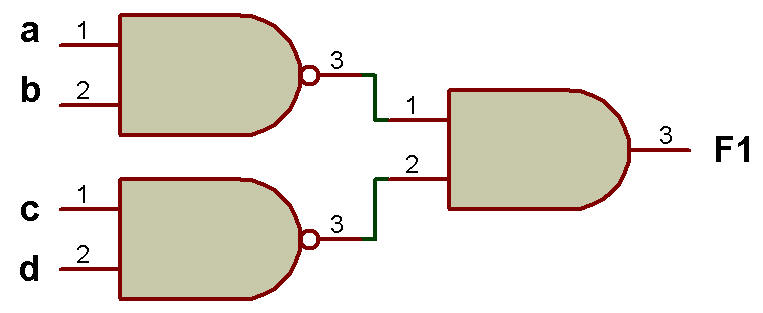
Exemple: Implémenter la fonction booléenne F1 = AB + CD + E
i. Utilisation de la porte AND-OR
ii. Utilisation de la porte NAND uniquement
Solution : F1 = AB + CD + E
Utilisation de la porte AND-OR.
L'implémentation à l'aide de la porte AND-OR peut être effectuée comme le montre la figure ci-dessous:
Figure (a) Utilisation de la porte AND-OR
ii. Utilisation de la porte NAND uniquement
La mise en œuvre à l'aide de la porte NAND peut être effectuée comme le montre la figure ci-dessous:
Figure (b) Utilisation de la porte NAND
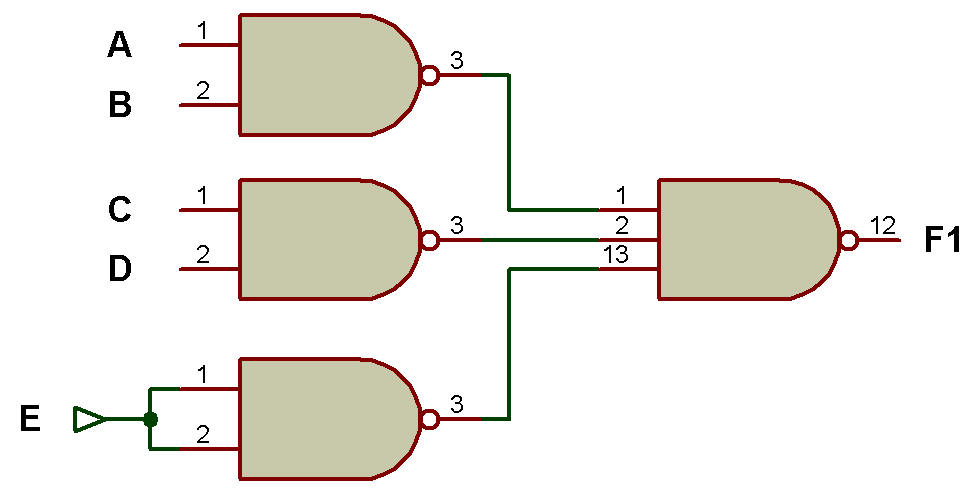
Le type d'implémentation illustré dans les figures (a) et (b) est une implémentation à deux niveaux car nous pouvons voir que l'entrée ne doit passer que par deux portes pour atteindre cette sortie.
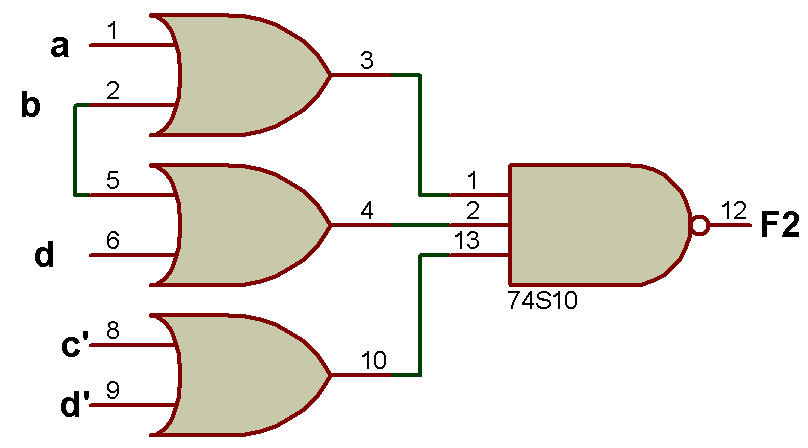
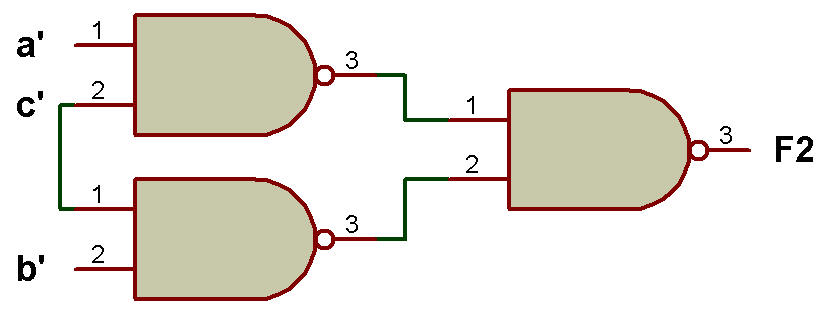
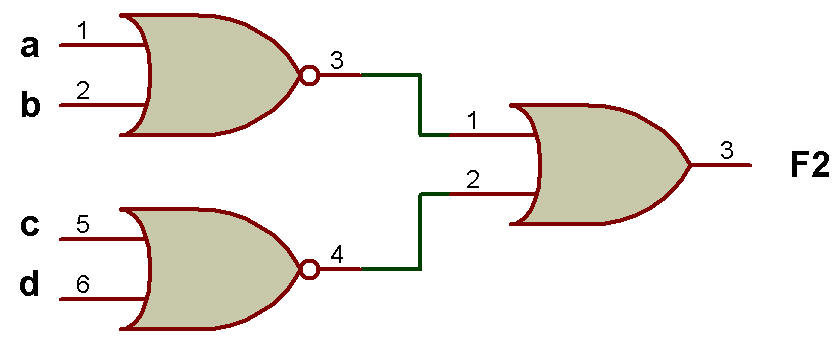
Exemple: Implémentez la fonction booléenne F2 (a, b, c) = (0, 2, 4) et F2 en utilisant uniquement la porte NAND.
Solution : F2 (a, b, c) = (0, 2, 4)
K-Map de F2
| bc | ||||
| b'c' | b'c | bc | bc' | |
| a | 1 | 1 | ||
| a' | 1 | |||
Lorsque nous mappons F2 (a, b, c) = (0, 2, 4) sur K-Map, nous obtenons F2 = a'c' + b'c simplifié.
L'implémentation de F2 en utilisant uniquement la porte NAND est illustrée dans la figure ci-dessous:
Implémentation de F2 en utilisant uniquement la porte NAND
Maintenant, F2' = (a'c' + b'c')'
= (a'c')' . (b'c')' -> en utilisant la loi de De-Morgan
= ((a')' +(c')') . ((b')' +(c')') -> en utilisant la loi de De-Morgan
= (a + c) . (b + c)
= c + (a . b) -> en utilisant le postulat 4
L'implémentation de F2' utilisant uniquement la porte NAND est illustrée dans la figure ci-dessous:
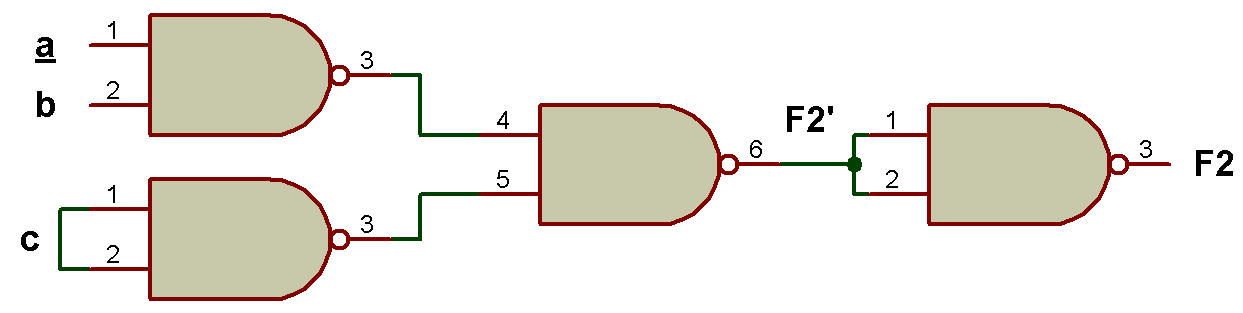
Notez que sur la figure, F2' lorsquelle est envoyée en entrée à la porte NAND, nous obtenons (F2')' en sortie, ce qui est égal à F2.
Il s'agit d'une implémentation à trois niveaux car pour obtenir une sortie, les entrées doivent passer par trois portes.
Habituellement, on suppose que toutes les variables d’entrée et leurs compléments sont disponibles ; au moment de la mise en œuvre du réseau logique, les inverseurs ne sont donc normalement pas comptés comme un niveau distinct dans le réseau.
Implémentation de la fonction booléenne à l'aide de la porte NOR :
Afin d'implémenter la fonction booléenne à l'aide de la porte NOR, la condition est que la fonction booléenne soit sous forme POS (Product of Sum).
Prenons un exemple d'implémentation d'une fonction booléenne à l'aide de la porte NOR.
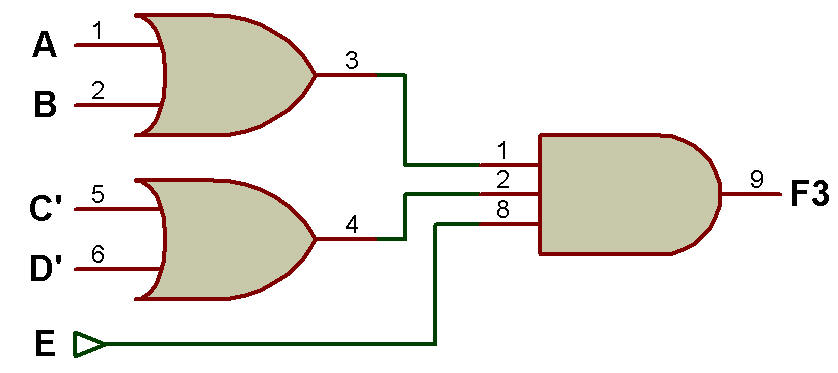
Exemple: Implémenter la fonction booléenne F3 = (A + B ) .(C + D') . E
i. Utilisation de la porte OU-ET
ii. Utiliser la porte NOR
Solution:
F3 = (A + B) . (C + D') . E
i. Utilisation de la porte OR-AND (OU-ET).
L'implémentation à l'aide de la porte OR-AND peut être effectuée comme le montre la figure ci-dessous:
Utilisation de la porte OR-AND
ii. Utilisation de la porte NOR uniquement
L'implémentation à l'aide de la porte NOR peut être effectuée comme le montre la figure ci-dessous:
Utilisation de la porte NOR uniquement
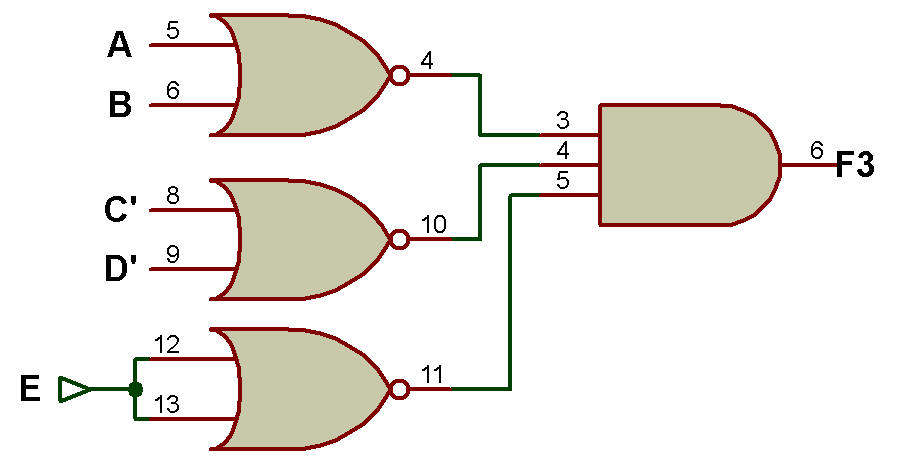
Ce type d'implémentation est une implémentation à deux niveaux car l'entrée ne doit passer que par 2 portes pour atteindre la sortie finale.
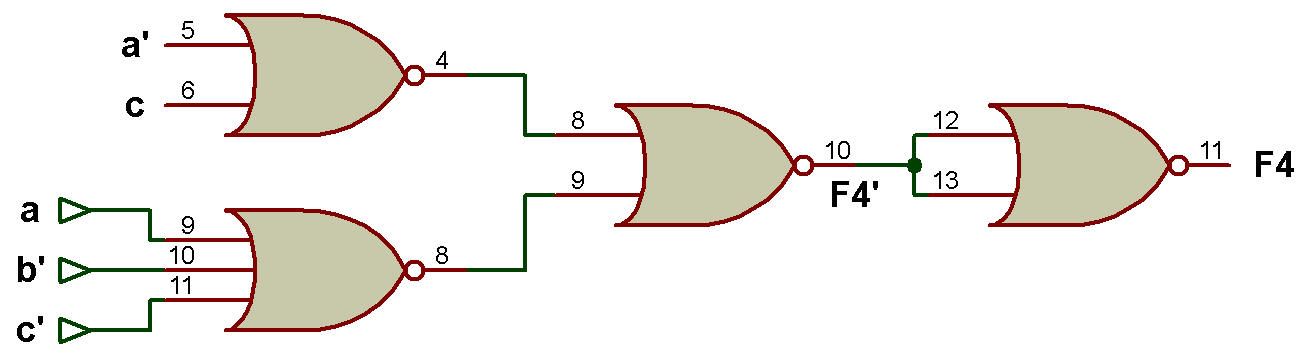
Exemple: Implémentez la fonction booléenne F4 (a, b, c) = π(0, 1, 2, 5) et F4' en utilisant uniquement la porte NOR.
Solution:
Lorsque nous mappons F4 (a, b, c) = π(0, 1,2, 5) sur K-Map, nous obtenons simplifié F4 = (a + c) . (b + c') . (a' + c).
Ceci est illustré à la figure ci-dessous:
| bc | ||||
| bc | bc' | b'c' | b'c | |
| a | 0 | 0 | 0 | |
| a' | 0 | 0 | ||
L'implémentation de F4 utilisant uniquement la porte NOR et l'implémentation de F4' utilisant uniquement la porte NOR sont illustrées à la figure ci-dessous:
Implémentation de F4 en utilisant uniquement la porte NOR
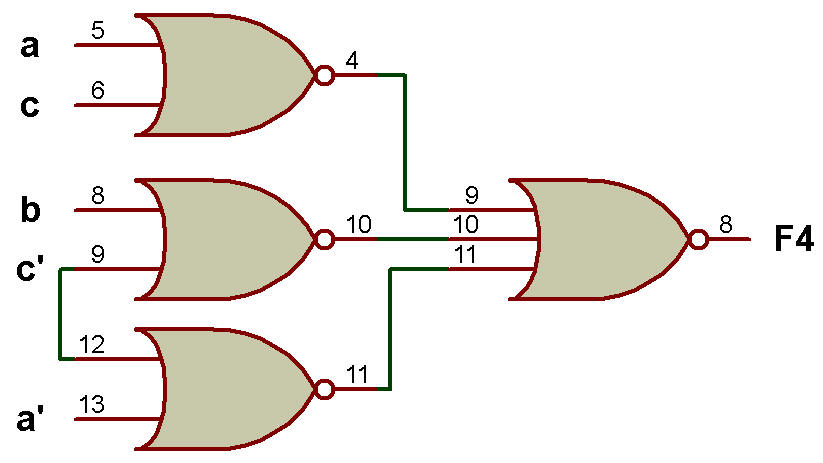
Maintenant, F4'= ((a + c) . ( b + c') . (a' + c'))'
= (a + c)' + (b + c')' + (a' + c')' -> fusion de la loi de De-Morgan
= (a '. c') + (b' . (c')') + ((a')'. (c')') -> en se référant à la loi de De-Morgan
= (a '. c') + (b' . c) + (a . c)
= (a', c') + c(b' + a)
Soit (a'. c') = x, c = y et (b' + a) = z
Donc, F4' = x + y . z
= (x + y) . (x + z)
En remplaçant les valeurs de x, y et z, nous obtenons, F4' = ((a'. c') + c) . ((a' . c') + b' + a)
= (a' + c) (a'c'+ b' +a) ->Parce que a + a'b = a + b
= (a' + c) [(a'c'+ a) +b')
= (a' + c) [(a +c')+ b') ->Parce que a + a'b = a + b
F4' = (a' + c) (a + b'+ c')
Implémentation de F4' en utilisant uniquement la porte NOR
2. Autre implémentation à deux niveaux de la fonction logique (booléenne) :
Dans la section précédente (i), nous avons expliqué comment les portes NAND et NOR sont utilisées pour créer une implémentation à deux niveaux d'une fonction logique.
Maintenant, dans cette section, nous discuterons d'autres implémentations à deux niveaux. Certaines portes NAND et NOR (pas toutes) autorisent le concept de logique filaire, dans lequel une connexion filaire entre les sorties de deux portes est réalisée de manière à remplir une fonction logique spécifique.
Par exemple, lorsque la sortie de deux portes NAND est reliée ensemble pour former une connexion filaire, elles agissent comme une logique ET câblée. Ceci est illustré à la figure ci-dessous:
Notez que la porte ET câblée est dessinée en utilisant la ligne passant par le centre de la porte.
La fonction logique implémentée dans les circuits de la figure est :
F1 = (a . b) . (c . d)'
= (ab + cd)' -> en utilisant la loi de De-Morgan
La fonction F1 est la fonction AND-OR-NOT.
De même, lorsque les sorties de deux portes NON-OU sont liées ensemble, elles agissent comme une logique OU câblée. Ceci est illustré à la figure ci-dessous:
Notez que la porte OU câblée est dessinée en utilisant la ligne passant par le centre de la porte.
La fonction logique implémentée dans les circuits de la figure est :
F2 = (a + b)' + (c + d)' = ((a + b) . (c + d))' -> La loi de De-Morgan
La fonction F2 est la fonction OR-AND-NOT.
Une porte à logique filaire ne crée pas de deuxième niveau physique car la logique filaire est simplement une connexion filaire.
Cependant, ces circuits illustrés sur les figures sont équivalents à des implémentations à deux niveaux.
Le premier niveau de la figure est constitué d'une porte NON-ET et le deuxième niveau est constitué d'une porte ET câblée.
De même, dans la seconde figure le premier niveau est constitué de portes NON-OU et le deuxième niveau est constitué de portes OU câblées.
Maintenant, dans la section suivante, nous discuterons des formes dégénérées et non dégénérées.
3. Formes dégénérées et non dégénérées :
Lorsque nous considérons quatre portes logiques principales : AND, OR, NOR et NAND
Il existe au total 16 combinaisons possibles qui peuvent être réalisées avec une implémentation à deux niveaux.
Cela signifie un type de portail au premier niveau et un type de portail au deuxième niveau.
Sur ces 16 combinaisons, 8 combinaisons sont appelées formes dégénérées car elles dégénèrent en une seule opération - soit OR, soit AND, soit NOR, soit NAND.
Ces 8 formes dégénérées sont présentées ci-dessous.
1. AND-AND(fonction exécutée - NAND)
2. AND-NAND (fonction exécutée - AND complément signifie NAND)
3. OR-OR
4. OR-NOR (fonction exécutée - OR complément signifie NOR)
5. NAND-OR (fonction exécutée - NAND)
6. NAND-NOR (fonction exécutée - AND)
7. NOR-NAND (fonction exécutée - OR) NOR-AND (fonction exécutée - NOR )
Voyons chacun d'eux un par un.
1. AND-AND :
Les figures ci-dessous montrent que la porte AND au premier niveau et la porte AND au deuxième niveau génèrent la fonction NAND et AND.
Porte AND au premier niveau et porte AND au deuxième niveau génère la fonction NAND

Les portes AND au premier niveau et 2 entrées AND la porte au deuxième niveau génèrent la fonction AND
2. AND-NAND (fonction exécutée - NAND) :
La figure ci-dessous montre que la porte and au premier niveau et la porte NAND au deuxième niveau génèrent la fonction NAND.

3. OR-OR:
Les figures ci-dessous) montrent que la porte OU au premier niveau et la porte OU au deuxième niveau génèrent la fonction Nor et OU.
La porte OR au premier niveau et la porte OR au deuxième niveau génèrent la fonction NOR

Les portes OR au premier niveau et la porte OR à 2 entrées au deuxième niveau génèrent la fonction OR
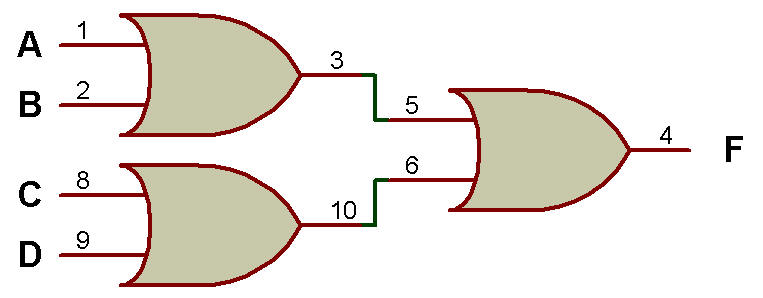
4. OR-NOR (fonction exécutée - NOR) :
La figure ci-dessous montre que la porte OR au premier niveau et la porte NOR au deuxième niveau génèrent la fonction NOR.

5. NAND-OR (fonction exécutée - NAND) :
La figure ci-dessous montre que la porte NAND au premier niveau et la porte OR au deuxième niveau génèrent la fonction NAND.
La porte NAND au premier niveau et la porte OU au deuxième niveau génèrent la fonction NAND
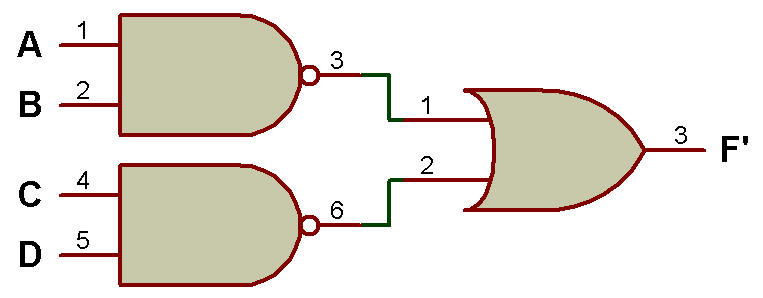
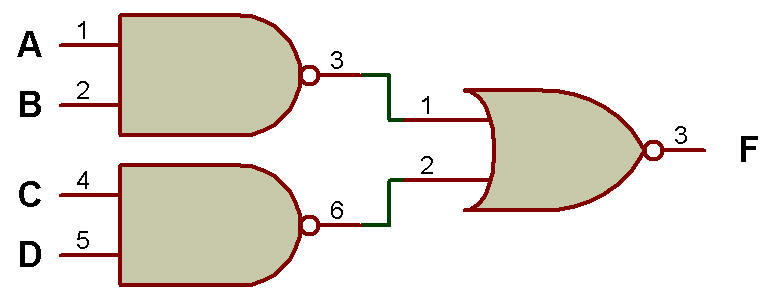
6. NAND-NOR (fonction exécutée - AND) :
La figure ci-dessous montre que la porte NAND au premier niveau et la porte NOR au deuxième niveau génèrent la fonction AND.
La porte NAND au premier niveau et la porte NOR au deuxième niveau génèrent la fonction AND
7. NOR-NAND (fonction exécutée - OR) :
La figure ci-dessous montre que la porte NOR au premier niveau et la porte NAND au deuxième niveau génèrent la fonction OR.
Porte NOR au premier niveau et porte NAND au deuxième niveau génère une fonction OR
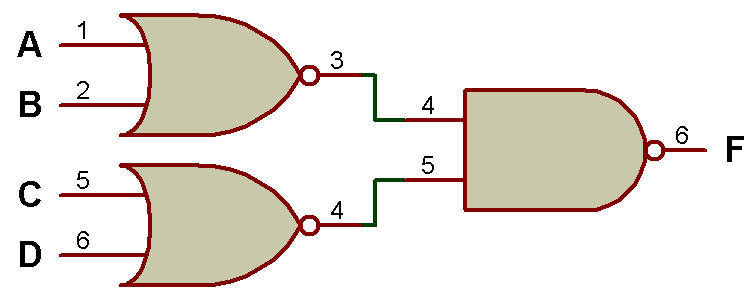
8. NOR-AND (fonction exécutée - NOR):
La figure ci-dessous montre que la porte NI au premier niveau et la porte ET au deuxième niveau génèrent la fonction NI.
La porte NOR au premier niveau et la porte AND au deuxième niveau génèrent la fonction NOR
Passons maintenant à 8 autres combinaisons.
Ces 8 combinaisons sont présentées ci-dessous et sont appelées formes non dégénérées.
| Formes non dégénérées | |
| FORME SOP | FORME POS |
| AND-OR | OR-AND |
| NAND-NAND | NOR-NOR |
| NAND-AND | NOR-OR |
| AND-NOR | OR-NAND |
Dans ces 8 formes non dégénérées, 4 formes sont utilisées pour l'implémentation de la fonction SOP (Sum of Product) et les 4 autres formes sont utilisées.
Discutons brièvement de ces formes non dégénérées.
Forme SOP
1. AND-OR a été discuté dans les sections précédentes lorsque nous parcourions les K-Maps.
Revoyons la forme AND-OR avec un exemple.
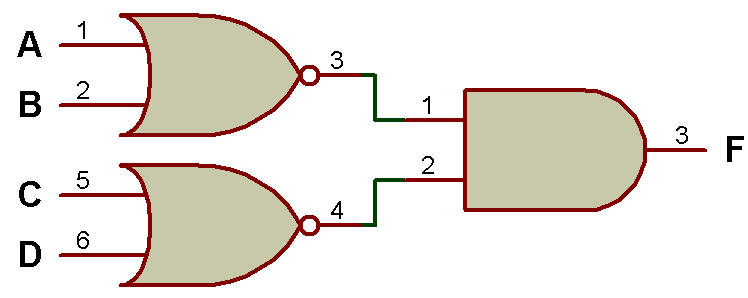
Soit F1 (a, b, c, d) = Σ(0, 1, 2, 5, 6, 8, 9, 10, 13)
Utilisation de AND au premier niveau et OR au deuxième niveau pour la mise en œuvre de la fonction SOP
En mappant F1 sur quatre variables K-Map, nous obtenons une fonction booléenne SOP simplifiée:
F1 = b'd' + c'd + a'cd'
2. NAND-NAND a déjà été discuté.
3. NAND-AND et
4. AND -NOT
NAND-AND et AND-NOR sont équivalents, nous en discuterons donc ensemble.
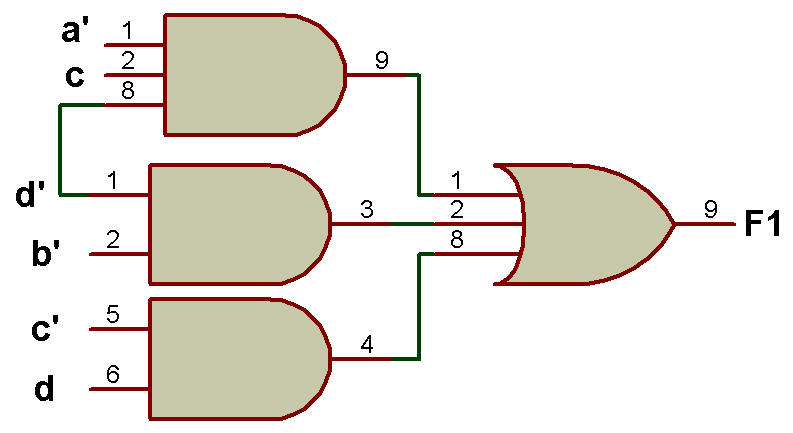
NAND-AND et AND-OR exécutent AND-OR-NOT comme indiqué ci-dessous avec un exemple.
F1 = (ab + c'd' + bd)'
L'implémentation de F1 à l'aide de NAND-AND est illustrée à la figure ci-dessous:
Implémentation de la fonction booléenne SOP F1 avec une porte NAND au premier niveau et une porte AND au deuxième niveau
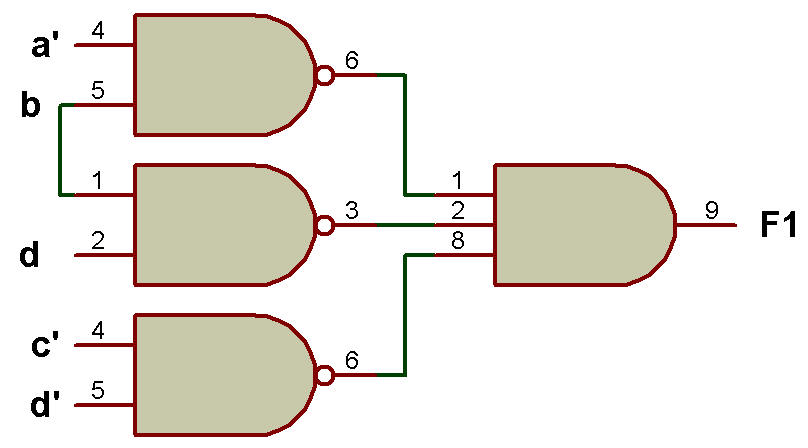
L'implémentation de F1 à l'aide de AND-NOR est illustrée à la figure ci-dessous:
Implémentation de F1 en utilisant la porte AND au premier niveau et la porte NOR au deuxième niveau
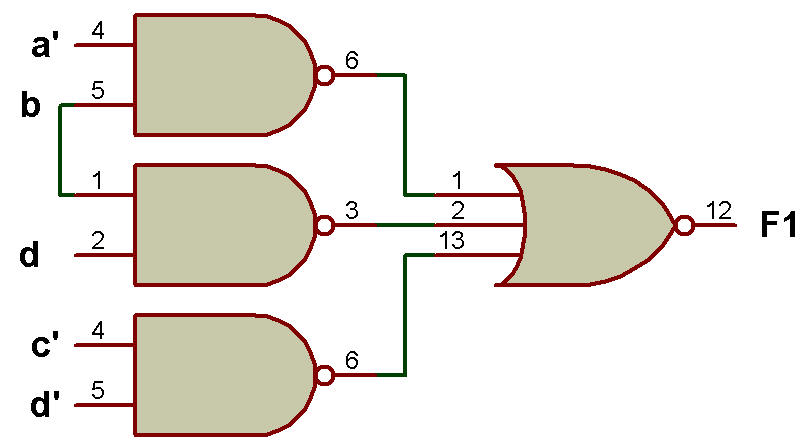
Nous allons maintenant discuter du formulaire POS pour les formes non dégénérées.
Forme POS
1. OR-AND a été discuté dans les sections précédentes lorsque nous parcourions les K-Maps.
Passons en revue OR-AND avec un exemple.
F2 (a, b, c, d) = π(0, 1, 2, 5, 6, 8, 9, 10, 13)
Le mappage F2 sur K-Map donne une fonction booléenne POS simplifiée F2 = (b + d) (c + d') (a + c'd).
L'implémentation de F2 à l'aide de OR-AND est illustrée à la figure ci-dessous:
Implémentation de F2 en utilisant la porte OR au premier niveau et la porte AND au deuxième niveau
2. NOR-NOR a déjà été discuté.
3. NOR-OR et
4. OR-NAND
NOR-OR et OR-NAND sont équivalents, nous en discuterons donc ensemble.
NOR-OR et OR-NAND effectuent OR-AND-NOT comme indiqué ci-dessous avec un exemple.
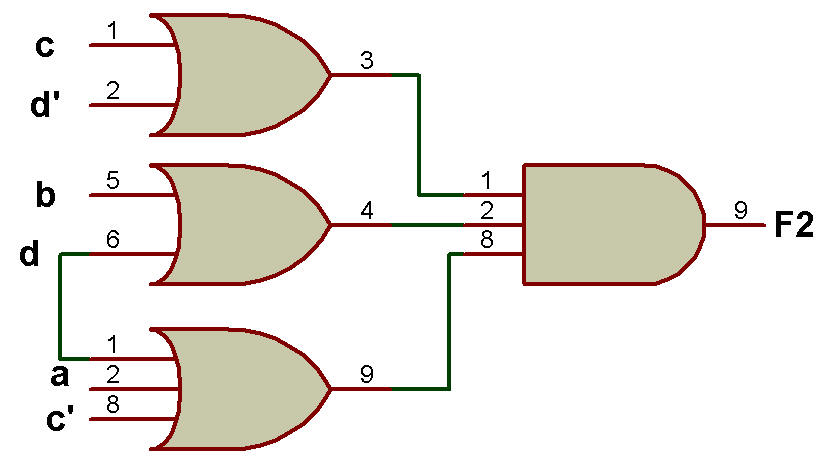
Étant donné, F2 = [(a + b) (c' + d') (b + d)]'
L'implémentation de F2 en utilisant NOR-OR est illustrée à la figure ci-dessous:
Implémentation de la fonction booléenne POS F2 avec porte NOR au premier niveau et porte OR au deuxième niveau.
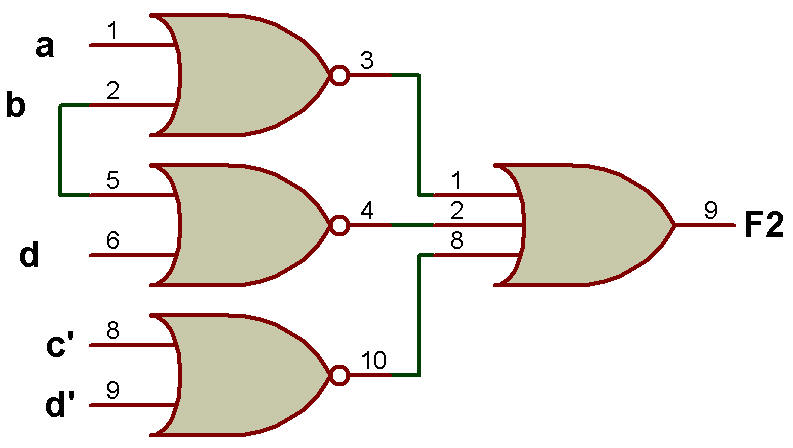
L'implémentation de F2 à l'aide de OR-NAND est illustrée dans la figure ci-dessous: