Les Dangers
Logique séquentielle asynchrone
Lorsque nous concevons des circuits séquentiels asynchrones, il faut veiller à deux choses pour le bon fonctionnement du circuit.
1. Le circuit ne doit pas présenter de condition de concurrence critique (les concurrences critiques et leur évitement sont déjà abordés dans la section Condition de concurrence.
2. Outre les concurrences critiques, il existe un autre aspect appelé hazard (danger) qui peut entraver le bon fonctionnement du circuit.
Le danger est en fait une condition dans laquelle la valeur binaire à la sortie d'un circuit change incorrectement pendant un moment (très peu de temps) en raison du retard de propagation et donc le danger conduit à un mauvais fonctionnement de l'ensemble du circuit.
Dans un circuit numérique chaque fois que la valeur binaire de l'entrée change, ce changement se propage à travers le circuit et atteint finalement la sortie du circuit pour apporter les modifications nécessaires à la valeur binaire de la sortie.
Le temps mis par le circuit pour propager l’effet du changement d’entrée à la sortie est appelé délai de propagation. Chaque composant numérique (portes, bascules, etc.) utilisé dans un circuit a son propre délai de propagation.
Dans cette section, nous discuterons des dangers (hazards) dans le circuit combinatoire et des dangers dans le circuit séquentiel.
Dangers dans le circuit combinatoire
Nous savons que le risque est en réalité une condition dans laquelle la valeur binaire à la sortie d'un circuit change momentanément en raison du délai de propagation.
Ce changement de sortie, bien que très court, ne devrait pas se produire car il conduit finalement à un mauvais fonctionnement du circuit.
Pour comprendre les dangers dans les circuits combinatoires, nous prendrons deux circuits comme exemple.
Le premier circuit est illustré à la figure A et le deuxième circuit est illustré à la figure B.

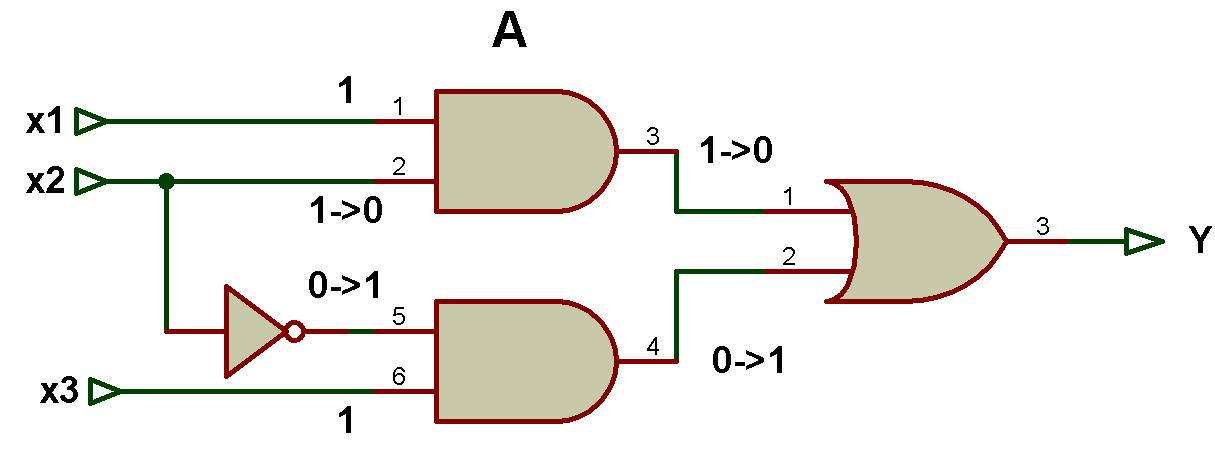
Commençons par le premier circuit comme le montre la figure ci-dessous A.
Ce circuit montre l'apparition d'un danger.
Dans le circuit, il y a trois entrées : x1, x2 et x3 ; une sortie Y ; deux portes ET ; une porte OU et une porte NON (un inverseur).
Au départ, x1, x2 et x3 sont égaux à « 1 », c'est-à-dire x1 = 1, x2 = 1 et x3 = 1.
Donc,
sortie à la porte 1 = x, AND x2 = 1
sortie à la porte 2 = x2' AND x3 = 0
sortie à la porte 3 = 1 OR 0 = 1
Supposons maintenant que x2 devienne « 0 »
Donc,
sortie à la porte 1 = x1 AND x2 = 0
sortie à la porte 2 = x2' AND x3 = 1
Mais, si le retard de propagation de l'inverseur est pris en compte, la sortie de la porte 2 peut passer à 0 au lieu de 1.
Le retard de l'inverseur peut faire passer la sortie de la porte 1 à « 0 » avant la sortie de la porte 2 passe à « 1 ».
Dans ce cas:
sortie à la porte 1 = x1 AND x2 = '0'
sortie à la porte 2 = x2' AND x3 = '0' (en raison du délai de propagation de l'onduleur)
Ainsi, sortie à la porte 3 = '0' OR '0' = '0' pendant un moment car le signal d'entrée de X2 est retardé pendant qu'il se propage à travers l'onduleur. C'est un danger (Hazard).
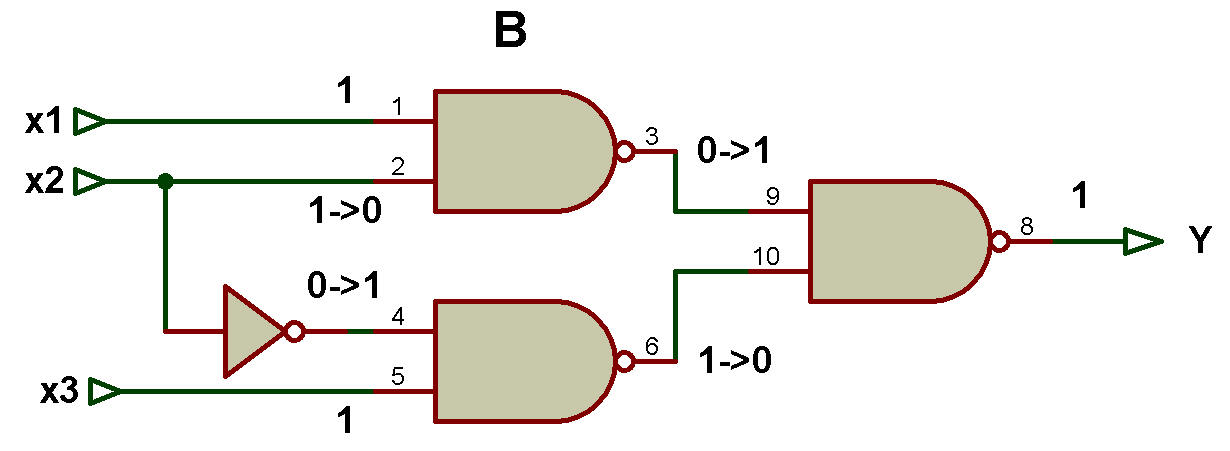
Si l'on considère le deuxième circuit comme le montre la figure B, ce circuit présente également un danger pour la même raison.
Dans le circuit il y a trois entrées : x1, x2 et x3 ; une sortie Y ; trois portes NAND et un onduleur.
Au départ, x1, x2 et x3 sont égaux à 1, c'est-à-dire x1 = 1, x2 = 1 et x3 = 1
Donc,
sortie à la porte 1 = x1 NAND x2 = 0
sortie à la porte 2 = x2' NAND x3 = 1
sortie à la porte 3 = 0 NAND 1 = 1
Supposons maintenant que x2 devienne 0, c'est-à-dire x2 = 0
Donc,
sortie à la porte 1 = x1 NAND x2 = 1
sortie à la porte 2 = x2' NAND x3 = 0
Mais la sortie de la porte 2 peut passer à « 1 » au lieu de « 0 », si le délai de propagation de l'inverseur est pris en compte.
Le retard de l'inverseur peut faire passer la sortie de la porte 1 à « 1 » avant que la sortie de la porte 2 ne passe à « 0 ».
Dans ce cas:
sortie à la porte 1 = x1 NAND x2 = 1
sortie à la porte 2 = x2' NAND x3 = 1 (en raison du retard de propagation de l'onduleur)
Ainsi, sortie à la porte 3 = 1 NAND 1 = 0 pendant un moment car le signal d'entrée de X2 est retardé pendant qu'il se propage à travers l'onduleur.
La fonction booléenne pour la sortie Y dans les figures ) et B est : Y = x, x2 + x2' x3 (voir K-Map pour Y sous forme SOP)
La fonction booléenne pour Y se présente sous la forme Somme du produit (SOP).
| K-Map pour Y (SOP) | |||||
| x2x3 | |||||
| x2'x3' | x2,x3 | x2x3 | x2x3' | ||
| x | x1' | 0 | 1 | 0 | 0 |
| x1 | 0 | 1 | 1 | 1 | |
Ce type d'implémentation peut faire passer la sortie à « 0 » alors qu'elle devrait rester à « 1 ».
Ce type de danger est appelé risque statique 1.
Si la fonction booléenne pour la sortie Y est exprimée sous forme de produit de somme comme :
Y = (x1 + x2') . (x2 + x3) (Voir K-Map pour Y dans la figure sous forme POS)
| K-Map pour Y (POS) | |||||
| x2x3 | |||||
| x2'x3' | x2,x3 | x2x3 | x2x3' | ||
| x | x1' | 0 | 1 | 0 | 0 |
| x1 | 0 | 1 | 1 | 1 | |
La fonction booléenne pour Y se présente sous la forme de produits de somme (POS).
Ce type d'implémentation peut faire passer la sortie à « 1 » alors qu'elle devrait rester à « 0 ».
Ce type de danger est appelé risque statique 0.
Un troisième type de danger existe également. Ce risque est appelé risque dynamique et fait changer la sortie trois fois ou plus alors qu'elle devrait passer de 1 à 0 ou de 0 à 1.
Les figures (a), (b) et (c) ci-dessous montrent les trois types de dangers.

Supposons que nous ayons un circuit implémenté à l'aide de portes AND-OR ou de portes NAND avec une expression booléenne pour la sortie exprimée sous la forme d'une somme de produit.
Désormais, si nous parvenons à supprimer le risque statique 1 dans ce circuit, cela garantit qu'un risque statique 0 ou un risque dynamique ne se produira pas non plus dans le circuit.
Pour détecter un danger dans un circuit donné, la K-Map de ce circuit est inspectée.
Par exemple, considérons le K-Map sous forme SOP.
Il s'agit de la K-Map sous forme SOP pour la sortie 'Y' du circuit de la figure A.
Dans ce K-Map, nous pouvons voir que le changement de la valeur binaire de x2 de 1 à 0 déplace le circuit du minterm 111 au minterm 101.
Chaque fois que le circuit passe d'un terme de produit à un autre, il est possible que pendant une courte période (par exemple un instant), aucun des termes du produit n'est égal à 1, ce qui donne lieu à une sortie « 0 » indésirable.
Maintenant, le danger s'est produit car le changement dans l'entrée x2 entraîne deux termes de produit différents couvrant les deux termes dans K-Map. Les deux termes produits sont : x1x2 et x2'x3.
Le remède pour éliminer un risque consiste à combiner les deux termes 111 et 101 qui provoquent un risque en un seul terme de produit qui chevauche les deux termes. Ceci est illustré dans la K-Map ci-dessous:
x2x3
x2'x3'
x2,x3
x2x3
x2x3'
x
x1'
1
x1
1
1
1
Ce K-Map est la même que celui du K-Map sous forme SOP, sauf que les minterms 111 et 101 sont combinés en utilisant un terme produit.
Il existe donc désormais 3 termes de produit : x1x2, x2 'x3 et x1x3.
Le terme produit x1x3 est le résultat lorsque les termes 111 et 101 sont combinés.
Le circuit obtenu à partir de la K-Map est désormais sans danger.
Ce circuit est illustré à la figure ci-dessous:
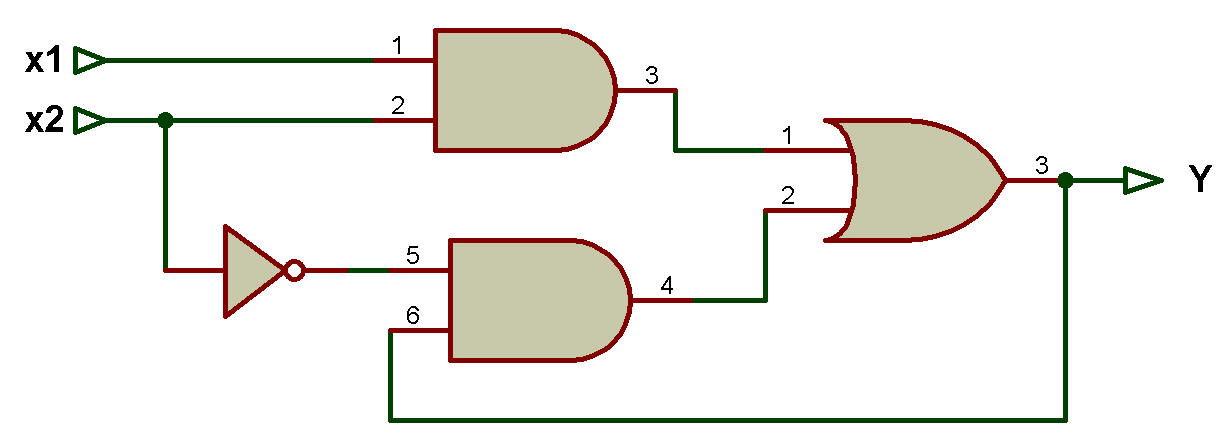
Il y a une porte supplémentaire utilisée dans le circuit pour générer le terme produit x1x3.
De la discussion ci-dessus, nous avons conclu que les dangers dans les circuits combinatoires peuvent être éliminés en combinant deux termes pouvant produire un danger avec un terme de produit commun.
La suppression des dangers nécessite l’ajout de portes redondantes au
circuit.
Dangers dans les circuits séquentiels
Dans un circuit séquentiel asynchrone, si, en raison d'un danger, la valeur binaire a été modifiée à tort pendant un moment et que cette valeur incorrecte est renvoyée (utilisée comme entrée de rétroaction), cette situation peut alors amener le circuit à passer dans un état stable incorrect.
Considérons la figure ci-haut pour comprendre cela.
Le tableau de transition est présentée dans le tableau ci-dessous et la K-Map pour la sortie Y est présentée ci-dessous:
Tableau de transition
| x1x2 | |||||
| 00 | 01 | 11 | 10 | ||
| Y | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | |
K-Map pour Y
| x2x3 | |||||
| x2'x3' | x2,x3 | x2x3 | x2x3' | ||
| x | x1' | 1 | |||
| x1 | 1 | 1 | 1 | ||
D'après le tableau de transition de la figure, les états stables corrects sont : Yx1x2 = 111 et Yx1x2 = 111.
Supposons actuellement que le circuit représenté sur la figure soit dans un état stable total correct avec yx1x2 = 111.
Supposons maintenant que x1 passe de « 1 » à « 0 », alors le prochain état correct total stable devrait être yx1x2 = 110.
Mais, en raison d'un danger dans le circuit, la sortie Y peut passer à « 0 » pendant un moment.
Si cette mauvaise valeur binaire de Y est réinjectée dans la porte 2 avant que la sortie de l'inverseur ne passe de « 0 » à « 1 » puis, la sortie de la porte 2 sera '0' AND '0' = '0'
Ainsi, le circuit passera à l’état stable total incorrect x1x2 = 010.
Ce problème de circuit passant d'un état stable à un état instable peut être éliminé en ajoutant une porte supplémentaire, comme le montre la figure.
Une autre façon d'éviter les risques statiques dans les circuits séquentiels asynchrones consiste à implémenter le circuit avec des verrous SR.
Implémentation avec des verrous SR
La mise en œuvre de circuits séquentiels asynchrones avec des verrous SR est un autre moyen efficace de rendre le circuit sans danger.
Considérons deux circuits comme le montrent les figures A et B.
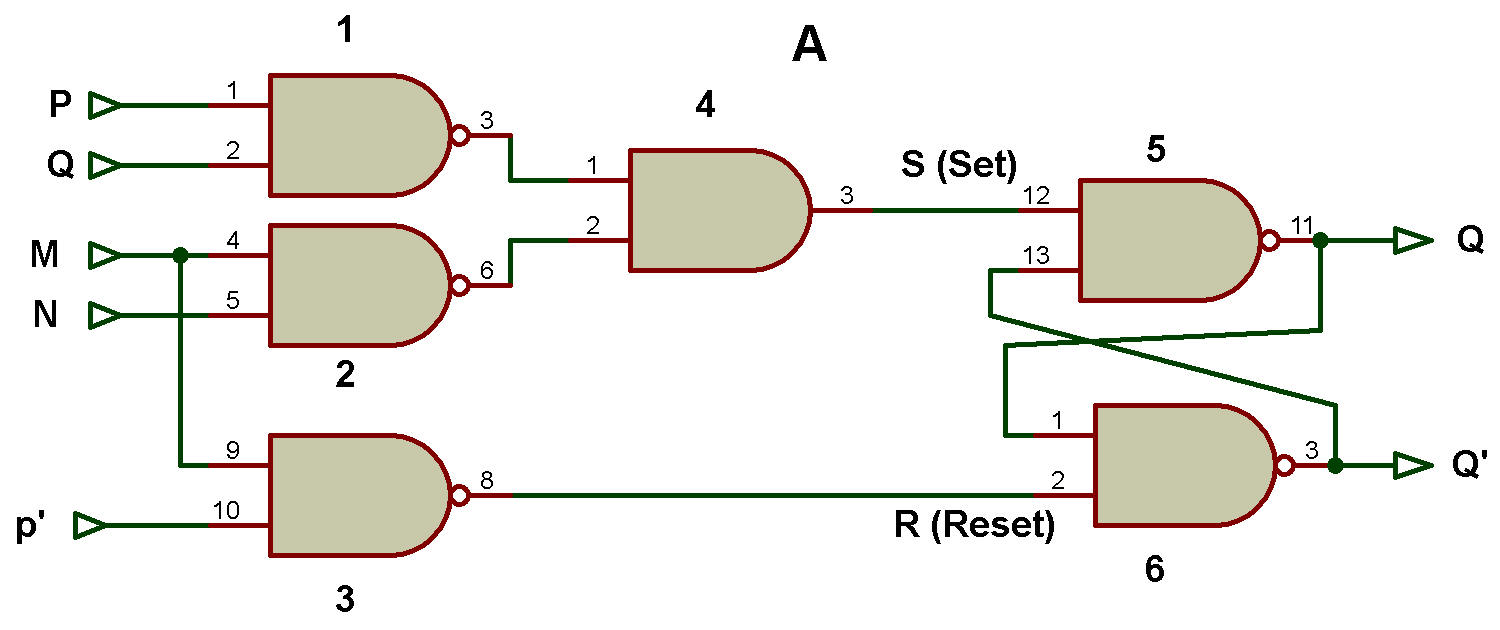
Dans la figure A, la somme de l'expression du produit est implémentée avec des portes NAND peut avoir un risque statique de 1 si les deux entrées de la porte 3 passent à 1, changeant la sortie de 1 à 0 pendant un instant.
Mais si la porte 3 fait partie d'un verrou, le signal momentané 1 n'aura aucun effet sur la sortie, car la troisième entrée de la porte 3 viendra du côté complémenté du verrou qui sera égal à 0 et maintiendra ainsi la sortie. en 1.
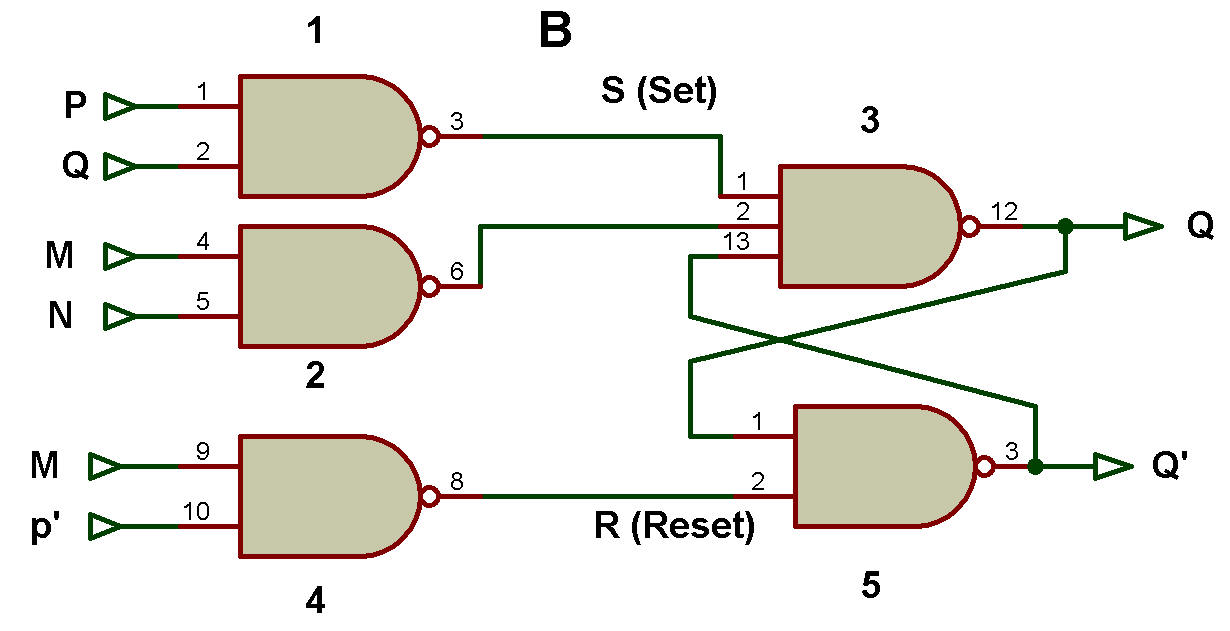
Pour comprendre à nouveau cela, considérons la figure B.
Puisqu'il s'agit d'un verrou NAND, nous devons appliquer les valeurs complémentées aux entrées :
Donc,
S = (PQ + MN)'= (PQ)'(MN)'
R = (P'M)'
La fonction booléenne pour la sortie Q est Q = (Q'S)' = [Q'(PQ)'(MN)']
Cette fonction est générée sur la figure B avec deux niveaux de portes NAND.
Si la sortie Q est égale à 1, alors Q' est égal à 0.
Si deux des trois entrées de la porte 3 passent à 1 en raison d'un danger, alors également la porte NAND associée à la sortie Q restera à 1 car Q' est maintenue à 0.
