Logique combinatoire
Introduction
Dans un circuit numérique, il existe deux logiques de conception :
i. Logique combinatoire :
La logique combinatoire est un circuit numérique mis en œuvre à l'aide de portes logiques, où la sortie dépend uniquement de la valeur d'entrée actuelle.
Tout changement dans l'entrée actuelle modifiera la sortie. Les circuits combinatoires sont conçus de telle sorte qu'ils n'ont aucune mémoire, ni synchronisation, ni retour. Des circuits logiques combinatoires sont utilisés pour implémenter des fonctions booléennes.
ii. Logique séquentielle :
La logique séquentielle est un circuit numérique conçu avec des portes et des éléments de mémoire. Ainsi, la sortie dépend non seulement de l'entrée actuelle mais également de la mémoire. L'élément de mémoire en logique séquentielle stocke l'état de sortie précédent ou passé.
À tout moment, la sortie du circuit logique séquentiel dépend donc de l'entrée et de la mémoire présentes.
Remarque :
Dans cette section, nous discuterons en détail des circuits logiques combinatoires et la prochaine section, on expliquera la logique séquentielle.
Le but de cette section est de discuter de la conception de circuits combinatoires et de l'analyse de divers circuits combinatoires.
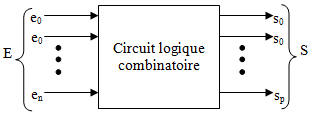
Un circuit combinatoire se compose de variables d'entrée, de portes logiques et de variables de sortie, comme le montre le schéma fonctionnel de la figure ci-dessous:
Schéma fonctionnel du circuit combinatoire

Comme le montre la figure, un circuit combinatoire peut avoir plusieurs entrées. Les entrées sont transmises à des portes logiques qui, à leur tour, en fonction de la fonction booléenne, produisent la sortie. La sortie peut être une ou plusieurs.
Ainsi, Sortie = f (entrée)
Où « f » est une fonction booléenne donnée, et l'entrée et la sortie sont des valeurs binaires (0 ou 1).
Le circuit logique combinatoire peut être classé comme indiqué ci-dessous:
|
Circuits logiques combinatoires |
||
|
Additionneur Soustracteur Comparateur PlLDs |
Multiplexeur Démultiplexeur Encodeur Décodeur |
Codeur Transcodeur Parité |
(Nous discuterons de presque chacune de ces logiques combinatoires et de ses sous-types un par un, mais avant cela, nous discuterons de la « Procédure d'analyse et de conception d'un circuit logique combinatoire »).
Procédure d'analyse et de conception pour les circuits logiques combinatoires
Procédure d'analyse
Dans la procédure d'analyse du circuit logique combinatoire, un schéma logique donné est analysé et la fonction booléenne correspondant à ce schéma logique est obtenue.
De plus, la table de vérité est dérivée soit du schéma logique donné, soit de la fonction booléenne.
Il est important qu'avant de démarrer la procédure d'analyse, le circuit logique donné soit vérifié qu'il s'agit d'un circuit logique combinatoire et non d'un circuit logique séquentiel.
Le schéma logique d'un circuit logique combinatoire est composé uniquement de portes logiques avec entrée et sortie, mais n'a pas de mémoire ni de chemin de rétroaction.
Une rétroaction est une connexion entre la sortie d'une porte et l'entrée de cette même porte ou vers l'entrée d'une autre porte dans un circuit logique donné.
Voici les étapes de la procédure d’analyse :
Étape 1 : Après avoir analysé le schéma logique indiquant qu’il s’agit d’un circuit logique combinatoire, la première étape consiste à attribuer différentes lettres (T,,T2....., ou X,,X2......ou autre) à toute la sortie des portes et écrit également la sortie de toutes les portes en termes de fonction booléenne.
Étape 2 : S'il y a des portes dont la sortie va à l'entrée de porte suivante, attribuez le symbole et les lettres comme indiqué à l'étape 1 à ces sorties de porte et obtenez également la fonction booléenne pour ces sorties de porte.
Étape 3 : Répétez les deux étapes 1 et 2 ci-dessus jusqu'à ce que toutes les sorties de portes soient étiquetées et que la fonction booléenne correspondant à chaque sortie de porte soit obtenue.
Étape 4 : Obtenez maintenant la fonction booléenne finale en combinant les fonctions booléennes générées à chaque sortie de porte.
Une simplification de la fonction booléenne finale est requise.
Pour trouver la table de vérité à partir d’un diagramme logique, les étapes sont les suivantes :
Étape 1 : Saisissez le schéma logique, déterminez toutes les variables d’entrée.
Supposons qu'il y ait "n" variables d'entrée, alors il y aura un total de 2n combinaisons de sortie.
Exemple : pour n = 4, il y aura 24 = 16 combinaisons de sortie (de 0000 à 1111).
Étape 2 : La table de vérité détermine d'abord la sortie pour toutes les sorties intermédiaires, puis pour les variables de sortie finales. (Comme dans l'exemple, les sorties intermédiaires sont X, X2, X3, X4, X5, X6 et X7 et les sorties finales sont F1 et F2).
Le processus d'analyse pour obtenir la fonction booléenne et la table de vérité est illustré à l'aide de l'exemple ci-dessous.
Exemple:
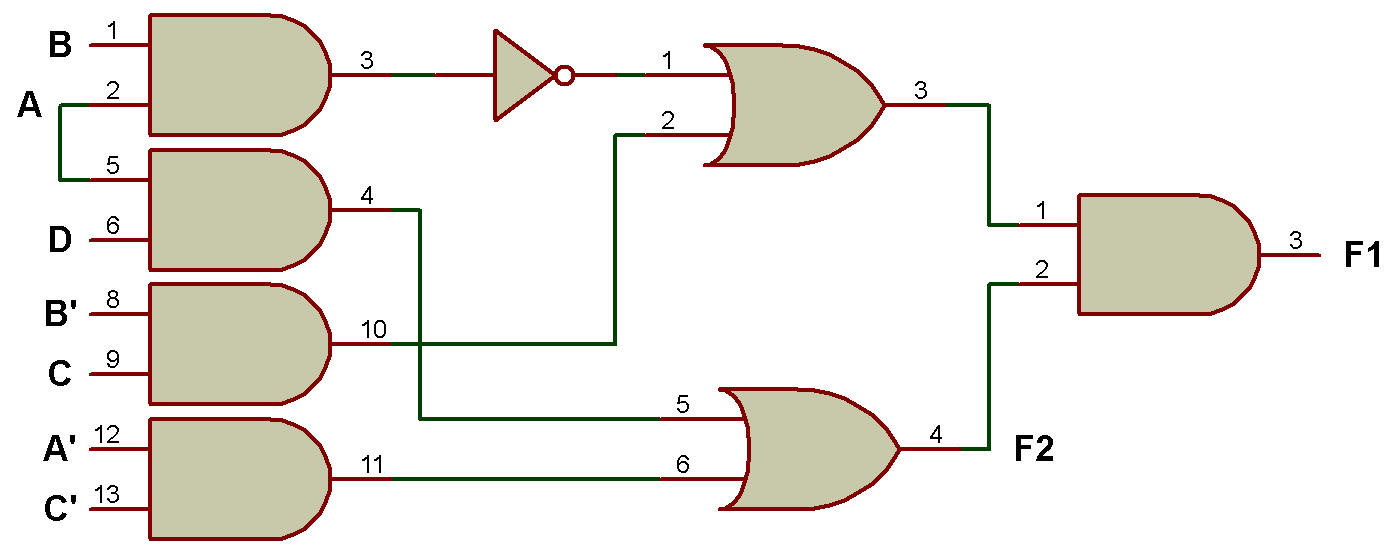
Obtenir la fonction booléenne pour les sorties F1 et F2 pour un schéma logique donné.
Obtenez également la table de vérité.
Solution :
Les étapes d'analyse sont les suivantes :
Étape 1 : Puisque le schéma logique illustré à la figure ci-haut est un circuit logique combinatoire, nous attribuons maintenant les lettres X1, X2, X3, X4 aux 4 premières sorties de la porte AND et obtenons les fonctions booléennes correspondant à X1, X2, X3, X4 comme indiqué dans le schéma logique de la figure ci-dessous.
Étape 2 : Étant donné que la sortie de ces portes ND va à l'entrée d'autres portes NOT et OR, nous attribuons la sortie de ces portes NOT et OR aux lettres X5, X6et X7.
Étape 3 : La fonction booléenne correspondant à X1, X2, X3, X4, X5, X6 et X7 est illustrée à la figure ci-dessous:
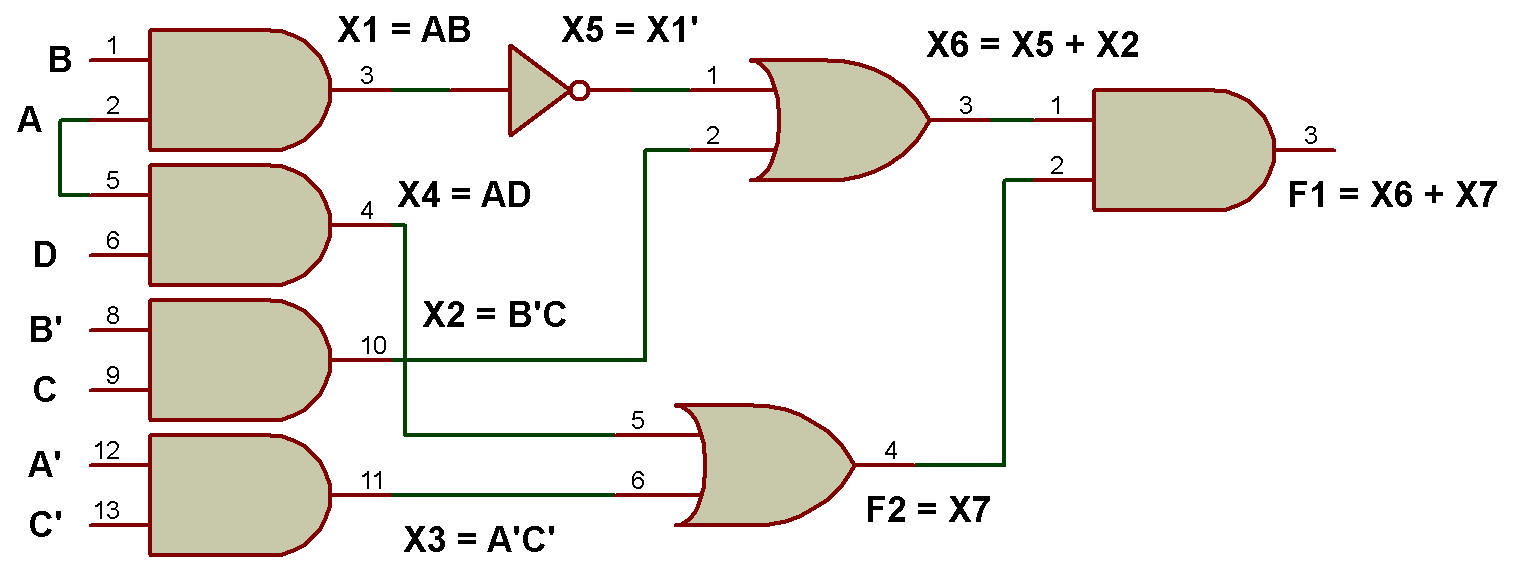
Étape 4 : Maintenant, nous obtenons enfin la fonction booléenne pour deux sorties finales F1 et F2: F1= X6 + X7 et F2= X7
F1= X6 + X7
= (X5 + X2) + (X3 + X4) ....... à partir de la figure
= (X1' + B'C) + (A'C AD) ....... à partir de la figure
= ((AB)' + B'C) + (A'C AD) ....... à partir de la figure
= ((A' + B') + B'C) + (A'C AD) ...... en utilisant la loi de De-Morgan (AB)' = A' + B'
En arrangeant les conditions que nous obtenons,
= A' + A'C' + AD + B' + B'C
= A'(1 + C')+ AD + B'(1 + C)
= A' + AD + B' ... en utilisant la loi (1 + X = 1) ........ de la figure
Donc F1 = A + AD + B'
Maintenant,
F2 = X7 = X3 + X4 = A'C + AD
Donc F2 = A'C + AD
Nous avons donc la fonction booléenne finale pour F1 et F2.
Nous allons maintenant obtenir la table de vérité pour F1et F2 (en utilisant les étapes comme expliqué dci-haut).
La table de vérité est présentée dans le tableau ci-dessous:
|
Table de vérité par l'exemple |
||||||||||||
| Variables d'entrée | Variables de sorite | |||||||||||
| A | B | C | D | X1 | X2 | X3 | X4 | X5 | X6 | X7 | F1 | F2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Nous passons maintenant à la procédure de conception pour un circuit logique combinatoire.
Procédure de conception
La procédure de conception d'un circuit combinatoire nécessite une déclaration décrivant quel est réellement le problème qui doit être conçu à l'aide d'un circuit combinatoire.
À l'aide des descriptions d'instructions, un schéma de circuit logique pour le problème donné est formé, ou en variante, à l'aide de l'ensemble de descriptions d'instructions de fonctions booléennes, on obtient un diagramme logique pour le problème donné.
Les étapes de la procédure de conception sont résumées comme suit :
i. Une déclaration décrivant quel est réellement le problème qui doit être conçu à l'aide d'un circuit combinatoire.
ii. À l'aide des descriptions d'instructions données, le nombre d'entrées et de sorties est déterminé.
iii. Les entrées et sorties reçoivent des lettres: a,b,c... ou A, B, C... ou x, y, z,... n'importe lequel.
iv. Une table de vérité est formée montrant la valeur des variables de sortie correspondant à différentes combinaisons de variables d'entrée.
v. La fonction booléenne pour la variable de sortie est obtenue et également simplifiée si nécessaire.
vi. En utilisant toutes les étapes ci-dessus, un diagramme logique pour le problème énoncé à l’étape 1 est obtenu.
Il est important de noter que pour une entrée "n" donnée, il y aura au total 2n sorties possibles (0 à 2n - 1).
Supposons que n = 4, alors les sorties sont de 0 à 24-1 = 0 à 15 sorties.
Les fonctions booléennes doivent également être simplifiées. La simplification peut être effectuée en utilisant la méthode algébrique, la méthode de tabulation ou la méthode K-Map (ces méthodes ont été discutées).
La simplification de la fonction booléenne aide à construire un circuit logique avec un nombre minimum de portes, un minimum d'interconnexions, une ligne d'entrée-sortie minimale et des circuits moins complexes.
