Multiplexeur 4:1
Multiplexeurs (MUX)
Les multiplexeurs sont des circuits combinatoires comportant de nombreuses lignes d’entrée et une ligne de sortie. La sortie à un instant particulier dépend de la ligne d'entrée sélectionnée.
La sélection de la ligne d'entrée est contrôlée par un ensemble de lignes de sélection (appelées sélecteurs de données).
En général, MUX a des lignes d'entrée 2n, 1 ligne de sortie et des lignes de sélection 'n' pour sélectionner l'une des lignes d'entrée 2n.
Le MUX peut être :
i. Multiplexeur 2:1
ii. Multiplexeur 4:1
iii. Multiplexeur 8:1
iv. MUX 16:1 et ainsi de suite.
Avant de discuter de ces MUX en détail, voyons quelques circuits intégrés MUX disponibles, résumés dans le tableau ci-dessous:
| Ic | Description |
| 74151A | 8:1 MUX |
| 74152 | 8:1 MUX |
| 74157 | Quad 2:1 MUX |
| 74158 | Quad 2:1 MUX |
| 74153 | Dual Quad 4:1 MUX |
| 74150 | 16:1 MUX |
L'expansion du MUX, l'implémentation de la fonction booléenne à l'aide de MUX et l'implémentation de la combinaison seront discutées un par un dans les sections à venir.
Multiplexeur 2:1
Le MUX 2:1 a deux lignes d'entrée I0 et I1, sur la ligne de sélection S et une ligne de sortie Y.
Nous savons qu'en général, le MUX a des lignes d'entrée de 2n, 1 ligne de sortie et des lignes de sélection 'n' pour sélectionner l'une des lignes d'entrée de 2n.
Donc en MUX 2:1, n=1, donc 21 = 2 entrées (I0 et I1).
La table de vérité pour le MUX 2:1 est présentée dans le tableau ci-dessous:
|
Select Line |
Entrées | Sorties | |
| S | I0 | I1 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
La K-Map pour la sortie Y est
illustrée dans la figure ci-dessous:
I0I1
S
00
01
11
10
0
1
1
1
1
1
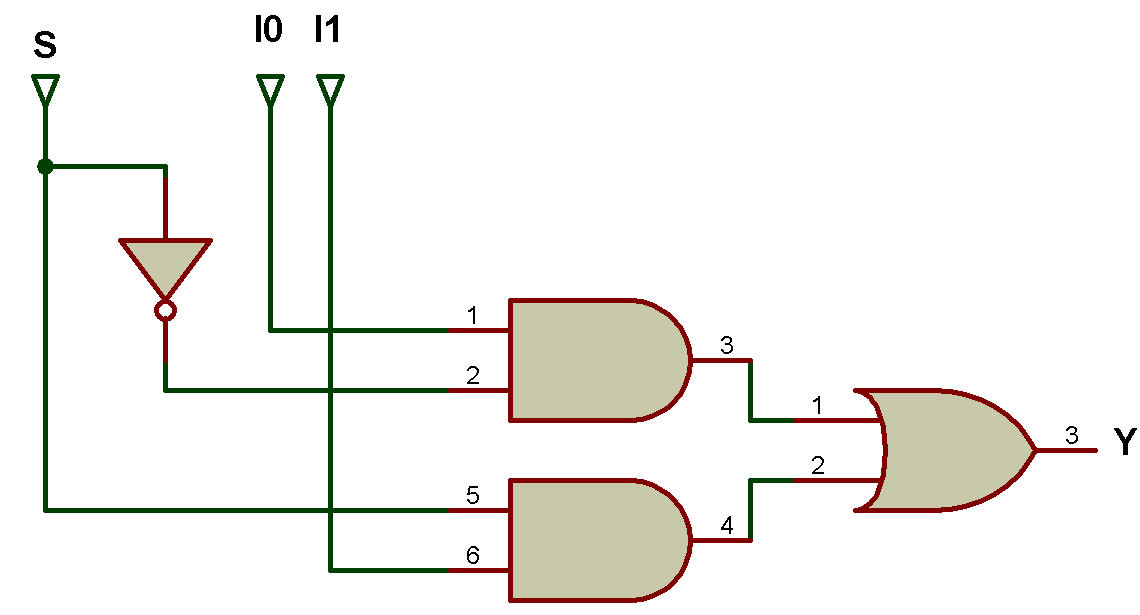
Le schéma logique du MUX 2:1 est présenté dans la figure
ci-dessous:

Multiplexeur 4:1
Le MUX 4:1 comporte quatre lignes d'entrée I0, I1, I2 et I3, deux lignes de sélection S0 et S1 et une ligne de sortie Y.
La table de vérité pour le MUX 4:1 est présentée dans le tableau ci-dessous:
| Select Line | Sorties | |
| S1 | S0 | Y |
| 0 | 0 | I0 |
| 0 | 1 | I1 |
| 1 | 0 | I2 |
| 1 | 1 | I3 |
D’après la table de vérité présentée dans le tableau 2.18, il est clair que le résultat Y est :
Y = S0'S1'I0 + S0S1'I1 + S0'S1I2 + S0S1I3
Le schéma logique du MUX 4:1 est présenté dans la figure
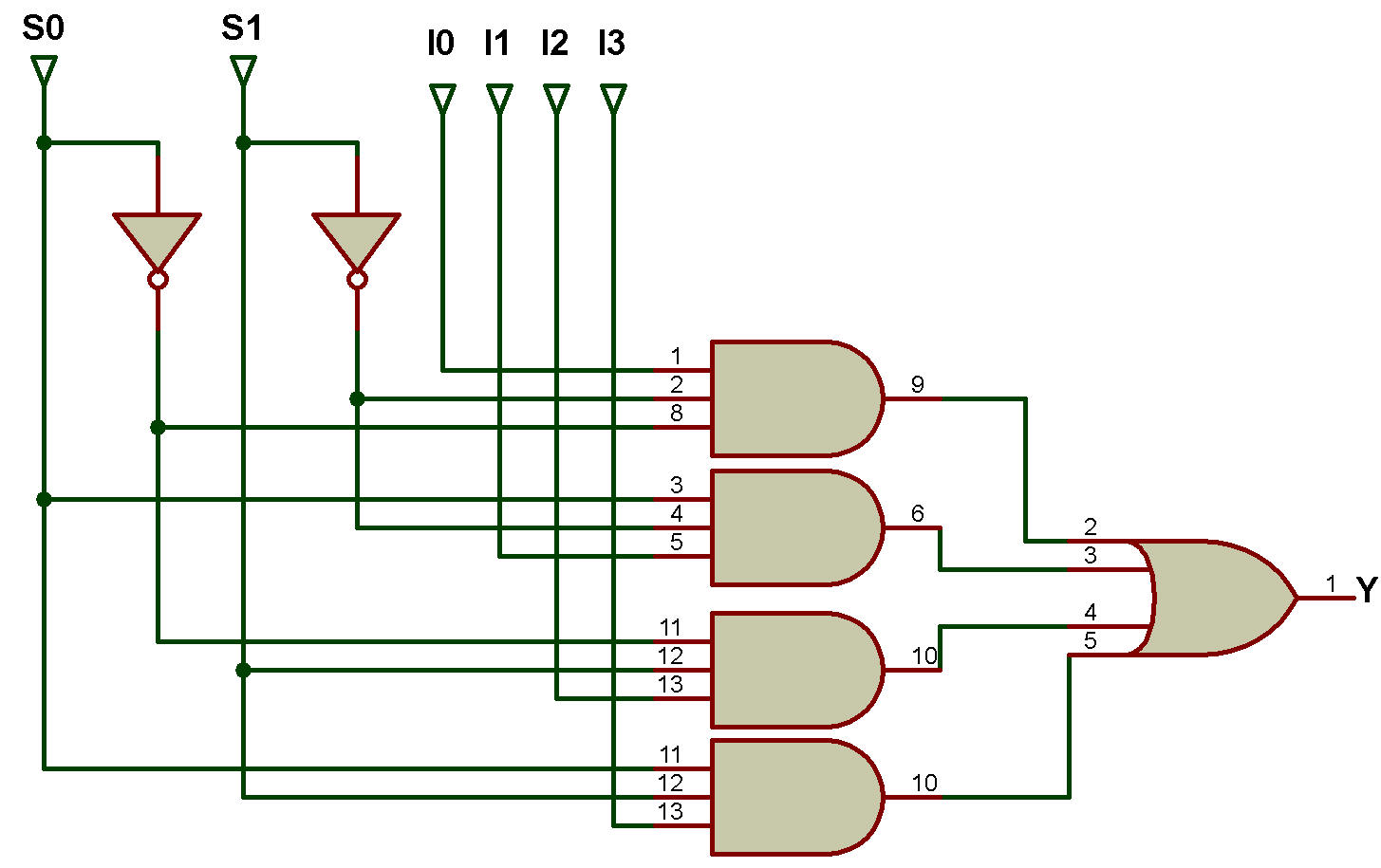
La figure ci-dessous montre le schéma fonctionnel du MUX 4:1.
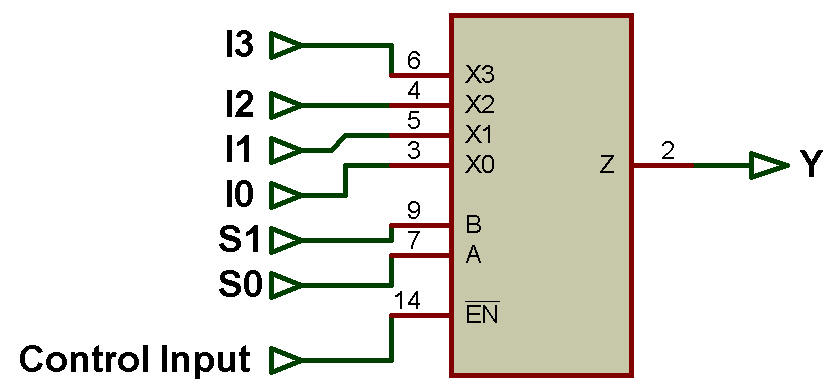
Le schéma fonctionnel montre 4 entrées - I0, I1, I2 et I3, une ligne de sortie Y et deux lignes de sélection S0 et S1.
Il y a une ligne d'entrée supplémentaire E (Enable ou Strobe). On l'appelle également entrée de contrôle.
Cette entrée E est utile lorsque nous souhaitons mettre en cascade deux ou plusieurs MUX (par exemple, mettre en cascade 4 MUX ou mettre en cascade 2 MUX selon les besoins).
La ligne d'entrée E est active à l'état bas, ce qui signifie qu'elle effectue l'opération requise lorsqu'elle est à l'état BAS (c'est-à-dire 0).
Cela signifie que lorsque E = 0, le MUX est activé. Lorsque E = 1, le MUX est désactivé et toutes les valeurs de sortie sont égales à « 0 », quelle que soit la valeur de S.
Multiplexeur 8:1
Le MUX 8:1 a huit lignes d'entrée I0, I1, I2 I3, I4, I5, I6 , et I7, trois lignes de sélection S0, S1et S2 et une ligne de sortie Y.
La table de vérité pour le MUX 4:1 est présentée dans le tableau ci-dessous:
| Select Line | Sorties | ||
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | I0 |
| 0 | 0 | 1 | I1 |
| 0 | 1 | 0 | I2 |
| 0 | 1 | 1 | I3 |
| 1 | 0 | 0 | I4 |
| 1 | 0 | 1 | I5 |
| 1 | 1 | 0 | I6 |
| 1 | 1 | 1 | I7 |
D’après la table de vérité présentée dans le tableau, il est clair que le résultat Y est :
Y = S0'S1'S2'I0 + S0S1'S2'I1 + S0'S1S2'I2 + S0S1S2'I3 + S0'S1'S2I4 + S0S1'S2I5 + S0'S1S2I6 + S0S1S2I7
Le schéma fonctionnel du MUX 8:1 est illustré dans la figure ci-dessous:
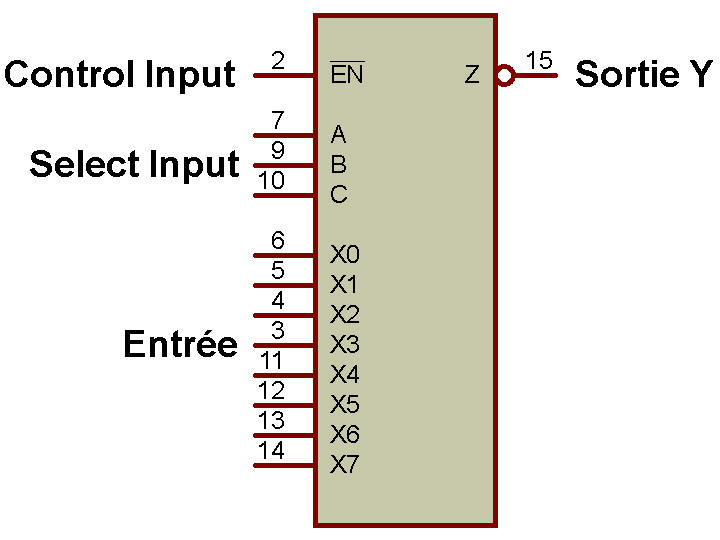
Nous allons maintenant discuter de certains IC MUX.
Multiplexeurs extensibles (ou en cascade)
Nous pouvons étendre le MUX pour former un MUX plus grand.
Cela se fait en mettant en cascade deux ou plusieurs MUX pour former un MUX plus grand.
Par exemple, deux MUX 4:1 peuvent être mis en cascade pour former un MUX 8:1.
Deux MUX 16:1 peuvent être mis en cascade pour former un MUX 32:1.
Prenons un exemple de conception de grands MUX utilisant deux ou plusieurs MUX connectés ensemble (en cascade).
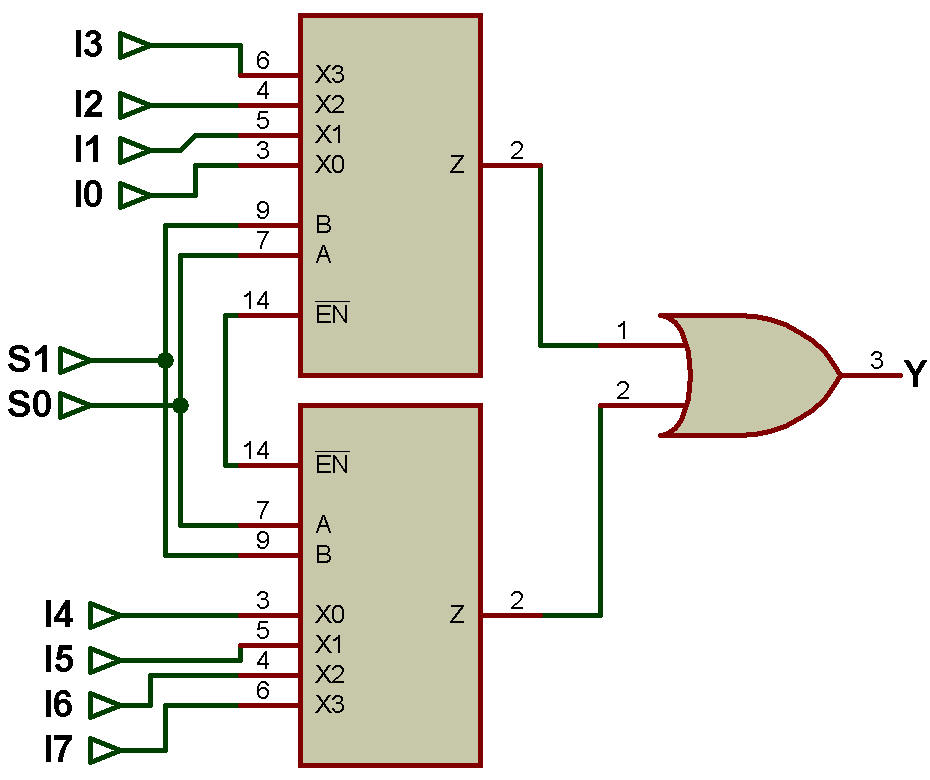
Exemple : Concevoir un MUX 8:1 en utilisant deux MUX 4:1.
Solution : ceci est illustré à la figure ci-dessous:
Implémentation de la fonction booléenne à l'aide de multiplexeurs
Discutons de quelques exemples d'implémentation de la fonction booléenne à l'aide de MUX.
Exemple: Implémentez la fonction booléenne «F» en utilisant un 8:1 MUX. F(X,Y,Z) = Σm(2,4,6,7)
Solution :
L'implémentation de la fonction booléenne F(X,Y,Z) = Σm(2,4,6,7) est illustrée à la figure ci-dessous:
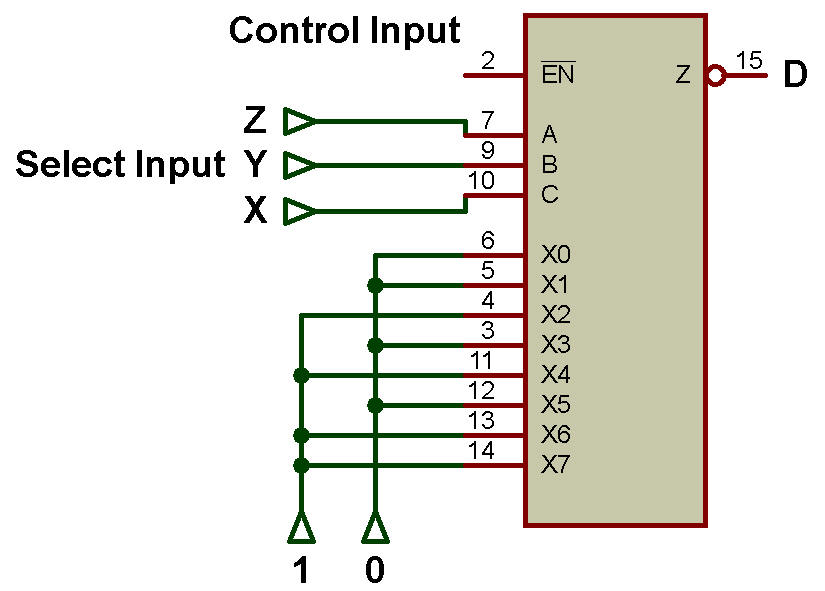
Les variables X, Y, Z sont utilisées comme ligne d'entrée de sélection pour MUX.
Les minterms 2,4,6,7 présents dans la fonction booléenne 'F' sont connectés à une ligne d'entrée ayant la valeur logique 1 (High).
Reste que tous les autres minterms 0,1,3,5 qui ne sont pas présents dans la fonction booléenne 'F' sont connectés à la valeur logique '0' (Faible).
Les entrées sont notées I0, I1, I2 I3, I4, I5, I6 , I7 et la sortie est notée D.
La méthode discutée dans l'exemple implémente la fonction booléenne avec des variables 'n' en utilisant un 2 : 1 MUX.
Cependant, il existe également une autre méthode alternative pour implémenter la fonction booléenne.
Cette méthode alternative dit que si une fonction booléenne a une variable 'n', utilisez les variables 'n-1' comme lignes de sélection et une variable restante comme ligne d'entrée dans MUX.
Ainsi, la fonction booléenne peut être implémentée en utilisant 2n-1: 1 MUX.
L'exemple ci-dessous implémente la fonction booléenne de l'exemple ci-haut en utilisant une méthode alternative.
Ainsi, la fonction booléenne de l'exemple ci-haut est implémentée en utilisant le MUX 4:1 dans l'exemple ci-dessous plutôt que le MUX 8:1.
Ceci est illustré à la figure ci-dessous.
Exemple: Implémentez la fonction booléenne «F» en utilisant un MUX 4:1 . F(X,Y,Z) = Σm(2,4,6,7)
Solution :
L'implémentation de la fonction booléenne F(X, Y, Z) = Σm (2,4,6,7) en utilisant 4:1 MUX est illustrée à la figure ci-dessous:
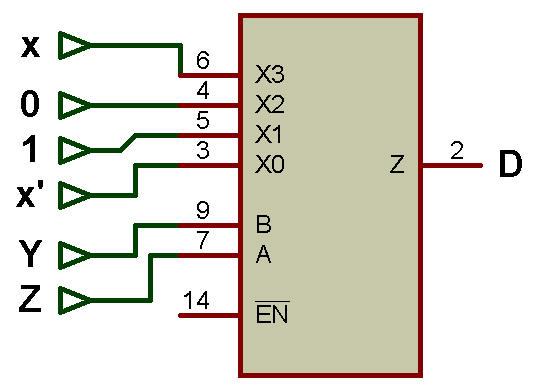
La fonction booléenne 'F' a 3 variables X, Y et Z, donc n=3. Par conséquent, 'n-l' = '3 - 1' = 2 variables sont utilisées comme lignes de sélection et la variable '1' restante est connectée à la ligne d'entrée.
Supposons que les 2 variables Y et Z de la fonction booléenne F soient utilisées comme lignes de sélection et que la variable X soit utilisée comme ligne d'entrée.
Les entrées de MUX sont 0, 1, X et X'. La sortie est « D ».
La table de vérité est présentée dans le tableau ci-dessous:
| Minterm | X | Y | Z | D |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 |
Le MUX montré sur la figure possède 4 entrées - I0 connectée à X, I1 connectée à 0, I2 connectée à 1, I3 connectée à X'.
Ces connexions d'entrée sont décidées à l'aide du tableau de mise en œuvre résumé dans le tableau ci-dessous:
| Col 1 | Col 2 | Col 3 | Col 4 | |
| Ligne 1 -> | I0 | I1 | I2 | I3 |
| Ligne 2 -> X | 0 | 1 | 2 | 3 |
| Ligne 3 -> X' | 4 | 5 | 6 | 7 |
| x | 0 | 1 | x' |
Comme le montre le tableau, nous avons la première ligne contenant les entrées de MUX, c'est-à-dire - I0, I1, I2 et I3.
Ensuite, dans les deuxième et troisième lignes, tous les minterms (0 à 7) sont disposés.
Comme le montre la table de vérité, X = 0 pour les minterms 0, 1, 2 et 3 et X = 1 pour les minterms 4, 5, 6 et 7.
La deuxième ligne est désignée par X et la troisième ligne par X'.
Les minterms présents dans la fonction booléenne 'F' sont misent en caractères gras puis en utilisant les règles suivantes (règles 1 à 4) les entrées I0, I1, I2 et I3 sont connectées à X, 0, 1 et X', respectivement.
Les règles décrites ci-dessous sont des règles générales et appliquées à toute implémentation de fonctions booléennes utilisant un MUX.
Règle 1 : Si le minterm de la deuxième ligne est encerclé et que le minterm de la première ligne n'est pas encerclé, alors I0 = X , signifie que I0 est connecté à l'entrée X [voir colonne 1].
Règle 2 : Si le minterm dans une colonne particulière n'est pas encerclé, alors I1 = 0, signifie I, est connecté à l'entrée 0 [Voir Colonne 2].
Règle 3 : Si les deux minterms sont encerclés dans une colonne particulière, alors I2 = 1, signifie que I2 est connecté à l'entrée 1 [Voir colonne 3].
Règle 4 : Si le minterm de la première ligne est encerclé et que le minterm de la deuxième ligne n'est pas encerclé, alors I3 = X', signifie que I3 est connecté à l'entrée X' [Voir colonne 4].
Notez que, dans l'exemple F(X, Y, Z) = Σ(2, 3, 4, 6), les variables Y et Z sont utilisées comme lignes de sélection.
Au lieu de cela, X et Y peuvent également être utilisés comme entrée de sélection et Z peut être connecté à la ligne d'entrée.
Dans ce cas, le tableau de mise en œuvre différera du tableau de mise en œuvre présenté dans le tableau ci-haut.
Comme le montre la table de vérité du tableau, Z =0 pour les minterms 0, 2, 4 et 6 et Z = 1 pour les minterms 1, 3, 5 et 7.
Le tableau de mise en œuvre est donc celui indiqué dans le tableau ci-dessous:
| Col 1 | Col 2 | Col 3 | Col 4 | |
| Ligne 1 -> | I0 | I1 | I2 | I3 |
| Ligne 2 -> Z' | 0 | 2 | 4 | 6 |
| Ligne 3 -> Z | 1 | 3 | 5 | 7 |
| 0 | 1 | Z' | Z |
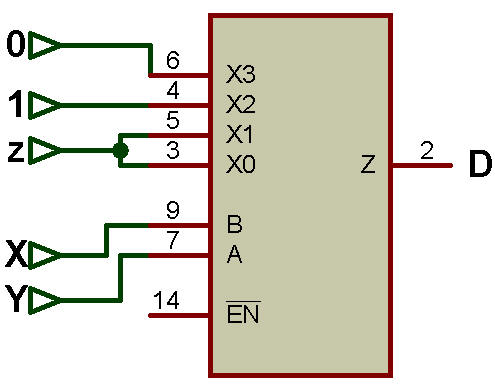
La figure ci-dessous montre l'implémentation de la fonction booléenne 'F' en utilisant le tableau d'implémentation tel que résumé dans le tableau, un MUX 4:1 est utilisé.
Exemple: Implémentez la fonction booléenne «F» en utilisant un MUX 8:1 . F (W, X, Y, Z) = Σm(0, 1,4, 7, 8, 11, 15)
Solution :
La table de vérité pour la fonction booléenne F (W, X, Y, Z) = Σm(0,1,4,7,8,11, 15) est présentée dans le tableau ci-dessous:
| Minterm | W | X | Y | Z | D |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 0 |
| 14 | 1 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 1 | 1 | 1 |
Le tableau de mise en œuvre est présenté dans le tableau ci-dessous et la mise en œuvre utilisant un MUX 8:1 est présentée dans la figure ci-dessous. X, Y et Z sont utilisés comme lignes de sélection et W est connecté à la ligne d'entrée.
Le tableau de mise en œuvre est présenté dans le tableau ci-dessous:
| Col 1 | Col 2 | Col 3 | Col 4 | Col 5 | Col 6 | Col 7 | Col 8 | |
| Ligne 1 -> | I0 | I1 | I2 | I3 | I4 | I5 | I6 | I7 |
| Ligne 2 -> W' | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Ligne 3 -> W | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 1 | W' | 0 | W | W' | 0 | 0 | 1 |
L'implémentation utilisant un MUX 8:1 est illustrée dans la figure ci-dessous:
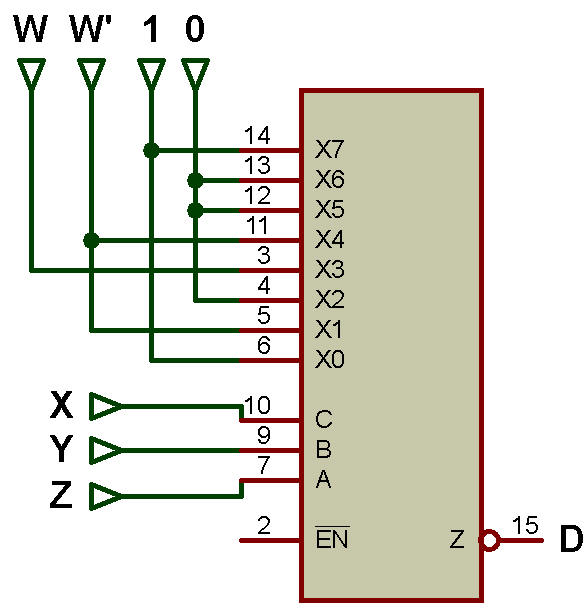
Implémentation d'un circuit combinatoire utilisant des multiplexeurs
Exemple: Concevoir un générateur de parité ODD pour 4 bits en utilisant un MUX 8:1.
Solution : La table de vérité pour le générateur de parité ODD pour 4 bits est présentée dans le tableau ci-dessous:
| W | X | Y | Z | ODD |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Le tableau de mise en œuvre est présenté dans le tableau ci-dessous.
I0, I1, I2... I7 sont des entrées. La sortie est D.
| Col 1 | Col 2 | Col 3 | Col 4 | Col 5 | Col 6 | Col 7 | Col 8 | |
| Ligne 1 -> | I0 | I1 | I2 | I3 | I4 | I5 | I6 | I7 |
| Ligne 2 -> W' | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Ligne 3 -> W | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| W' | W | W | W' | W | W' | W' | W |
L'implémentation utilisant un MUX 8:1 est illustrée dans la figure ci-dessous:
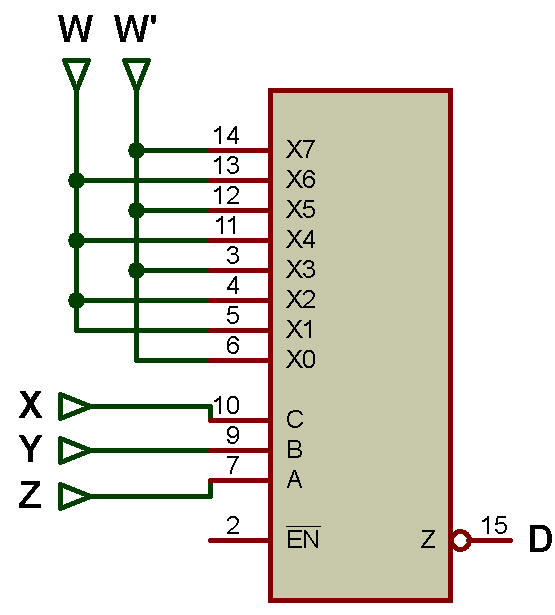
Applications du MUX
i. Utilisé comme sélecteur de données pour sélectionner une sortie parmi plusieurs lignes d'entrée.
ii. Implémentez un circuit logique combinatoire et une fonction booléenne.
iii. Registre pour enregistrer le transfert de données.
iv. Générateur de train d'impulsions.
v. Système de multiplexage temporel et fréquentiel.
vi. Conversions A/D (Analogique-Numérique) et D/A (Numérique-Analogique) et bien d'autres encore...
