Nombres binaires non signés et signés
Nombres binaires non signés
Les nombres non signés sont des nombres non négatifs. Comme son nom l'indique, non signé signifie des nombres qui ne nécessitent pas de signe pour se représenter.
Ainsi, tous les nombres positifs (car les nombres positifs ne nécessitent pas de signe) sont couverts par des nombres non signés.
La plage de stockage des nombres non signés à l'aide de 'n' bits est comprise entre 0 et 2n-1.
Par exemple, si n=8 bits, alors nous pouvons représenter des nombres de 0 à 28-1 = 0 à 255.
Si n = 3 bits, alors 0 à 23-1 = 0 à 7.
Comme nous le savons, les ordinateurs stockent tout sous forme binaire, donc pour stocker les nombres non signés, ils sont d'abord convertis sous forme binaire.
Supposons maintenant que pour un nombre donné de bits «n», si le nombre à stocker est inférieur à «n» bits, alors «0» est complété à gauche du nombre binaire pour obtenir un total de «n» bits.
Par exemple, étant donné n = 16, la plage va donc de 0 à 216-1.
Supposons maintenant que nous voulons mettre en mémoire (259). Les étapes sont indiquées ci-dessous :
Étape 1 : Convertissez (259)10 en binaire. (259)10= (100000011)2
Étape 2 : Étant donné que le nombre binaire ci-dessus est inférieur à 16 bits, il est donc complété par des zéro à gauche.
Étape 3 : Ainsi, le numéro (259)10 sera stocké en mémoire sous le nom (000000010000001)2.
Problème de débordement et de sous-débordement dans les numéros non signés :
Supposons que nous ayons n = 8, donc la plage va de 0 à 28-1, c'est-à-dire de 0 à 255.
Supposons maintenant qu'après quelques calculs, nous obtenions que le nombre m = 305 soit stocké avec n = 8 bits.
Cette condition est un débordement, car 305 est en dehors de la plage 0 à 255 (avec n = 8 bits).
Pour stocker 305, nous avons besoin de n - 9 bits,
comme (305)10 = (100110001)2, c'est-à-dire qu'un total de 9 bits sont requis.
Le sous-dépassement est la condition dans laquelle, après un calcul, nous obtenons un nombre « m » inférieur à zéro (nombre négatif), nous disons alors qu'un sous-dépassement s'est produit, car les nombres non signés ne peuvent stocker que des nombres positifs.
Nombres binaires signés
Les nombres signés, comme leur nom l'indique, nécessitent un signe pour représenter et stocker les nombres dans les ordinateurs.
Dans les nombres signés, le MSB (Most Significant Bit) est utilisé comme bit de signe pour stocker le signe du nombre.
Si le bit de signe=1, le nombre est négatif, si le bit de signe=0, le nombre est positif.
Les bits restants (bit de signe sortant) sont utilisés pour représenter le nombre.
Les nombres signés représentent ainsi 2n-1 nombres positifs et -(2n-1-1) nombres négatifs avec 'n' bits donnés.
Il existe deux manières utiles de représenter et de stocker les nombres négatifs signés.
Ceux-ci sont:
Représentation de la magnitude signée d'un nombre (Signed Magnitude Representation)
Système de complément ou méthode de complément (Complement system or complement method)
Discutons brièvement de chacun d'eux.
Représentation de grandeur signée
Dans la représentation de grandeur signée avec n bits, le MSB est utilisé pour le signe (1 pour un nombre négatif et 0 pour un nombre positif) et les bits (n-1) restants sont utilisés pour représenter la grandeur des nombres.
D'où le nom de la magnitude signée.
Exemple:
Représentez comment le nombre -(28)10 avec n = 8 bits est stocké en mémoire.
Solution:
-(28)10=(111100)2
Ainsi, avec n - 8 bits, -(28)10 est stocké en mémoire comme indiqué ci-dessous:
| Signe du nombre | Ajout de 0 | Magnitude du nombre | |||||
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
Exemple: Représentez comment le nombre -(3)10 avec n = 8 bits est stocké en mémoire.
Solution:
-(3)10= (10000011)2
Ainsi, avec n = 8 bits, -(3)10 est stocké en mémoire comme indiqué ci-dessous :
| Signe du nombre | Magnitude du nombre | ||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Exemple: Représentez comment les nombres -(7)10 et +(7)10 avec n = 8 bits sont stockés en mémoire.
Solution:
-(7)10= (10000111)2
Ainsi, avec n = 8 bits, -(7)10 est stocké en mémoire comme indiqué ci-dessous.
| Signe du nombre | Magnitude du nombre | ||||||
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
+(7)10=(00000111)2
Ainsi, avec n = 8 bits, +(7)10 est stocké en mémoire comme indiqué ci-dessous :
| Signe du nombre | Magnitude du nombre | ||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Exemple: Représentez comment les nombres -(7)10 et +(7)10 avec n = 4 bits sont stockés en mémoire.
Solution:
-(7)10=(1111)2
Ainsi, avec n = A bits, -(7)10 est stocké en mémoire comme indiqué ci-dessous:
| Signe du nombre | Magnitude du nombre | ||
| 1 | 1 | 1 | 1 |
+(7)10=(0111)2
Ainsi, avec n = 4 bits, +(7)10 est stocké en mémoire comme indiqué ci-dessous:
| Signe du nombre | Magnitude du nombre | ||
| 0 | 1 | 1 | 1 |
L’autre façon de représenter les nombres signés négatifs est la méthode du complément qui est expliquée ci-dessous.
Système complémentaire
Les systèmes complémentaires sont une autre façon de représenter des nombres négatifs dans un ordinateur. Les systèmes complémentaires simplifient également opération de soustraction.
Pour tout système numérique, de base b, il peut y avoir deux types de système complémentaire :
i. le complément de b's
ii. complément b - 1's
Pour la base du système de numérotation binaire b = 2, les compléments sont donc :
Le complément de b's = le complément à 2
et le complément b -1's = le complément à 1
Complément de 1's et de 2's pour les nombres binaires
Le complément d'un nombre binaire est obtenu en inversant simplement chaque bit d'un nombre binaire.
Le bit « 0 » est remplacé par « 1 » et le bit « 1 » est remplacé par « 0 ».
Exemple: Trouvez le complément à 1 de 110100101.
Solution :
Complément à 1 de 110100101 = 001011010 (chaque bit est inversé)
Exemple: Trouver le complément à 1 de 11001.
Solution :
Complément à 1 de 11001 = 00110 (chaque bit est inversé)
Si le complément à 1 est appliqué deux fois sur un nombre binaire, le nombre binaire obtenu sera le même que le nombre binaire d'origine.
Ceci est illustré ci-dessous.
Numéro binaire d'origine = 001101
complément à 1= 110010
Complément à 1 encore = 001101
Complément à deux :
Le complément à deux est obtenu en prenant le complément à un d'un nombre binaire, puis 1 est ajouté pour obtenir le complément à deux.
Exemple: Trouvez le complément à 2 de 11010.
Solution :
Complément à 1 de 11010 = 00101
Complément à 2 de 11010 = 00101 + 1 =00110
Exemple: Trouver le complément à 2 de 00011101.
Solution :
Complément à 1 de 00011101 = 11100010
Complément à 2 de 00011101 = 11100010 + 1 = 11100011
Si le complément à 2 est appliqué deux fois sur un nombre binaire, le nombre binaire obtenu sera le même que le nombre binaire d'origine.
Ceci est illustré ci-dessous.
Nombre binaire d'origine = 11001 Complément à 2 = 00111 Complément à 2 à nouveau = 11001
Représenter le nombre binaire signé en utilisant le complément à 1 et à 2
L'utilisation principale des compléments à 1 et à 2 est de représenter un nombre signé sur l'ordinateur. L'utilisation du complément à 1 et à 2 simplifie la représentation et le codage des nombres négatifs.
De plus, ce système de complément permet d'effectuer une soustraction en utilisant une addition modifiée.
Aujourd'hui, la plupart des ordinateurs effectuent des soustractions en utilisant le complément à 1 ou à 2.
Ainsi, avec les circuits d'addition, seules l'addition et la soustraction peuvent être effectuées, ce qui rend les circuits internes beaucoup plus simples.
Règles de représentation (stockage) des nombres binaires signés à l'aide du complément 1 et 2
Étape 1 : Le nombre signé donné est transformé en binaire (s'il n'est pas sous forme binaire).
Étape 2 : Si le nombre est positif, stockez ce nombre tel quel.
Étape 3 : Si le nombre est négatif, prenez le complément de 1 ou de 2 pour stocker (représenter) le nombre.
Exemple: Montrez comment le nombre +(15)10 est stocké en mémoire.
Solution:
Les étapes sont les suivantes:
Étape 1 : Le nombre donné +(15)10 est changé en binaire.
+ (15)10=(00001111)2
Étape 2 : Le nombre est positif ; stockez donc ce numéro 00001111 tel quel.
Exemple: Montrez comment les nombres + (12)10 et -(12)10 sont stockés en mémoire.
Solution:
Les étapes pour +(12)10 sont les suivantes :
Étape 1 : Le nombre donné +(12)10 est changé en binaire.
+(12)10= (00001100)2
Étape 2 : Le nombre est positif ; stockez donc ce numéro 00001100 tel quel.
Les étapes pour -(12)10 sont les suivantes :
Étape 1 : Le nombre donné -(12)10 est changé en binaire
(12)10= (00001100)2
Étape 2 : Le nombre est négatif; donc soit prendre le complément à 1, soit le complément à 2
le complément à 1 de 00001100 = 11110011
Donc, -(12)10 = 11110011 sous la forme du complément de 1.
Si le complément à 2 est pris alors le complément à 2 de 00001100 = 11110100
Donc, -(12)10 = 11110100 sous forme de complément à 2.
Exemple: Montrez comment les nombres +(50)10 et -(50)10 sont stockés en mémoire.
Solution:
Les étapes pour +(50)10 sont les suivantes :
Étape 1 : Le nombre donné +(50)10 est changé en binaire
+(50)10=(0110010)2
Étape 2 : Le nombre est positif ; stockez donc ce numéro 0110010 tel quel.
Les étapes pour -(50)10 sont les suivantes :
Étape 1 : Le nombre donné -(50)10 est changé en binaire
-(50)10 = (0110010)2
Étape 2 : Le nombre est négatif ; donc soit prendre le complément à 1, soit le complément à 2
le complément à 1 de 0110010= 1001101
Donc, -(50)10 = 1001101 sous la forme du complément à 1.
Si le complément à 2 est pris alors,
le complément à 2 de 0110010= 1001110
Donc, -(50)10= 1001110 sous forme de complément à 2.
Règles de récupération des nombres stockés en mémoire au format complément 1 ou 2 :
a. Si le LSB (Left Significant Bit) est 1, cela signifie que le nombre est négatif, donc le complément à 1 ou à 2 est appliqué pour obtenir le nombre binaire d'origine.
Si LSB est 0, alors le nombre est positif donc pas besoin de prendre le complément à 1 ou à 2.
b. Ce nombre binaire est ensuite converti et représenté en décimal.
c. Si le nombre est négatif, attachez un signe négatif.
Exemple: Récupérer l'entier 11100001 stocké en mémoire en notation complément à 1.
Solution:
a. LSB est 1, cela signifie que le nombre est négatif, nous appliquerons donc le complément à 1
11100001
00011110 complément à 1
b. Remplacez ce nombre en décimal (00011110)2 = (30)10.
c. Un signe négatif est joint. La réponse finale est donc (-30)10.
Exemple: Récupérer le nombre décimal de 1100101 stocké en notation complément à 2.
Solution:
a. LSB est 1, signifie que le nombre est négatif.
Prenez le complément à 2 car le nombre est stocké dans la notation complément à 2
1100101
0011010 Complément à 1
0011011 Complément à 2
b. Changez ce nombre en décimal
(0011011)2 = (27)10
c. Un signe négatif est joint. La réponse finale est donc (-27)10.
Exemple: Récupérer 0010111 stocké en notation complément à 2.
Solution:
a. LSB est 0, donc le nombre est positif.
b. Pas besoin de prendre le complément à 2.
Convertissez directement le nombre en décimal. (0010111)2 = (23)10
c. Le signe est facultatif puisque le nombre est positif. Donc, réponse finale (+23)10.
Affichage d'un nombre de 4
bits dans les quatre représentations
(non signé, signé, complément à 1 et
complément à 2)
Le tableau ci-dessous résume un nombre de 4 bits dans les quatre représentations :
non signé, signé, complément à 1 et complément à 2.
Tableau: Affichage d'un nombre de 4 bits dans les quatre représentations
| Nombre 4 bits | non signé | signé |
complément à 1 |
complément à 2 |
| 0000 | 0 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 | 1 |
| 0010 | 2 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 | 3 |
| 0100 | 4 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 | 5 |
| 0110 | 6 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 | 7 |
| 1000 | 8 | 0 | -7 | -8 |
| 1001 | 9 | -1 | -6 | -7 |
| 1010 | 10 | -2 | -5 | -6 |
| 1011 | 11 | -3 | -4 | -5 |
| 1100 | 12 | -4 | -3 | -4 |
| 1101 | 13 | -5 | -2 | -3 |
| 1110 | 14 | -6 | -1 | -2 |
| 1111 | 15 | -7 | 0 | -1 |
Comme le montre le tableau, avec 4 bits on peut représenter :
• 0 à 15 nombres en notation non signée 24 = 16.
• 0 à 7 (Positif) et (0 à -7) en notation signée (MSB est un signe réservé).
• 0 à 7 et 0 à -7 dans le complément à 1 (le complément à 1 comporte deux zéros).
• 0 à 7 et -1 à -8 en complément à 2 (seulement 1 zéro en complément à 2).
Débordement de nombres binaires signés
Supposons que nous ayons en mémoire +4, et que nous y ajoutions +9, le résultat devrait être +13, mais il s'agit d'un cas de débordement.
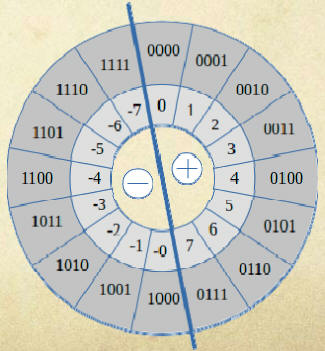
Donc pour obtenir la bonne réponse, avec la figure ci-dessous, commencer à compter à +5 et comptez 9 unités dans le sens des aiguilles d'une montre pour obtenir la réponse -5.
Représentation des débordements positifs et négatifs

De même, si nous avons le nombre -3 et que nous soustrayons -10, alors la bonne réponse n'est pas -13.
Pour obtenir la bonne réponse, commencez juste après -3 (à partir de -2) et comptez 10 unités dans le sens inverse des aiguilles d'une montre pour obtenir la bonne réponse +1.
