Procédure d'analyse
Logique séquentielle asynchrone
La procédure d'analyse d'un circuit séquentiel asynchrone consiste à comprendre le comportement de fonctionnement global du circuit donné.
Par comportement de fonctionnement, nous entendons la manière dont un circuit génère une sortie en fonction des variables d'entrée et du changement d'état interne.
La procédure d'analyse de tout circuit séquentiel asynchrone donné est effectuée en construisant une table de transition et une table de flux.
La stabilité du circuit séquentiel asynchrone donné est également analysée pour garantir de bonnes performances globales.
La table de transition, la table de flux et la stabilité du circuit séquentiel asynchrone donné sont discutées un par un dans la section à venir.
Nous discuterons également de la condition de concurrence qui est un aspect important de la procédure d'analyse.
Tableau de transition
Pour comprendre la table de transition d'un circuit séquentiel asynchrone, prenons un exemple.
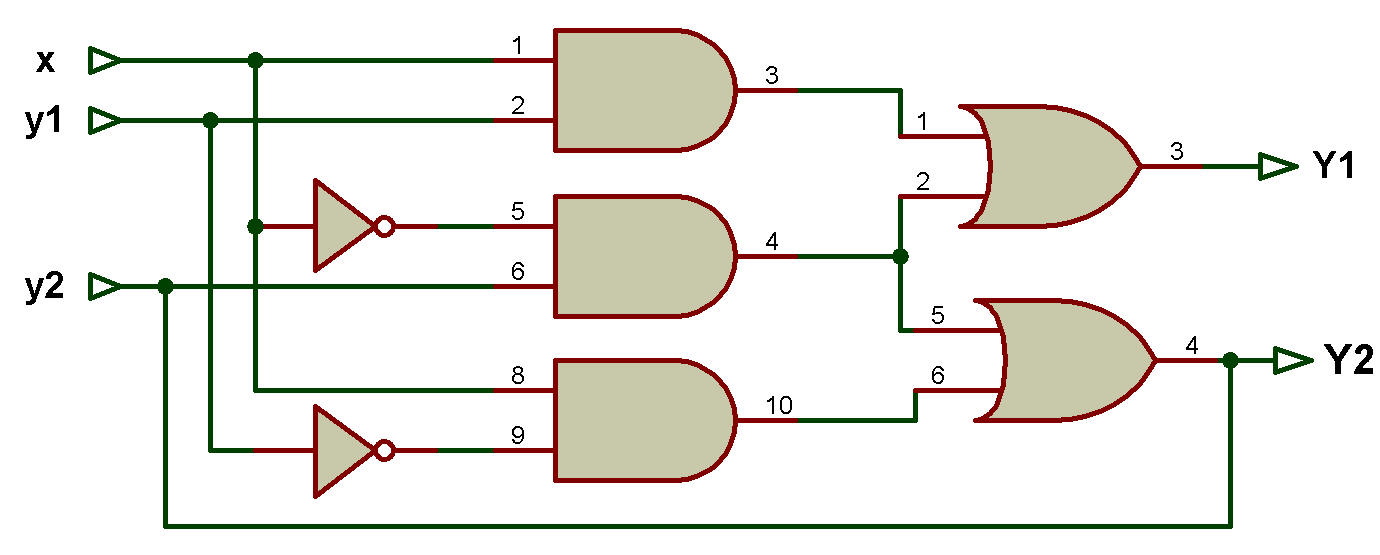
Le diagramme de l'exemple est présenté Figure ci-dessous:

De la figure, on peut noter que :
• Il existe une variable d'entrée principale x.
• Il existe deux variables secondaires y1 et y2.
• Il existe deux variables d'excitation Y1 et Y2.
L'expression booléenne des variables d'excitation Y1 et Y2 est :
Y1 = xy1 + x'y2
Y2 = xy'1 + x'y2
Nous allons maintenant dessiner une K-Map pour Y1 et Y2.
Les K-Map pour Y1 et Y2 sont représentées respectivement sur les tableaux ci-dessous:
| K-Map Y1 | K-Map Y2 | ||||||
| x | |||||||
| C1 | C2 | C3 | C4 | ||||
| x' | x | x' | x | ||||
| y1y2 | R1 | y1'y2' | 0 | 0 | R5 | 0 | 0 |
| R2 | y1'y2 | 1 | 0 | R6 | 1 | 1 | |
| R3 | y1y2 | 1 | 1 | R7 | 1 | 0 | |
| R4 | y1y2' | 0 | 1 | R8 | 0 | 1 | |
Les lignes et les colonnes des deux K-Maps reçoivent un nom, par exemple la première ligne est R1 et la première colonne est C1 dans la K-Map Y1.
De même, la première ligne est R5 et la première colonne est C3 dans la K-Map Y2 et ainsi de suite.
Le tableau de transition (TT) est présenté dans le tableau ci-dessous:
| x | ||||
| C1 | C2 | |||
| x'(0) | x(1) | |||
| y1y2 | R1 | y1'y2' (00) | 00 | 01 |
| R2 | y1'y2 (01) | 11 | 01 | |
| R3 | y1y2 (11) | 11 | 10 | |
| R4 | y1y2' (10) | 00 | 10 | |
Chaque ligne et colonne des K-Map forme un carré.
Le tableau de transition est obtenu en combinant les valeurs binaires des carrés correspondants des deux K-Maps.
Par exemple, la première ligne et la première colonne de la table de transition contiennent la valeur binaire 00. Ceci est obtenu comme suit :
Valeur binaire de la première ligne et de la première colonne du tableau de transition (TT)
R1C1 (TT) = valeur binaire de R1C1 (voir K-Map Y1) combinée avec la valeur binaire de R5C3 (voir K-Map Y2) = 00.
De même,
La valeur binaire de la première ligne et de la deuxième colonne du tableau de transition (voir K-Map Y1) = valeur binaire de R, C2 (voir la figure 5.2(b)) valeur binaire combinée de R5C4 (voir K-Map Y2) = 01.
De même, toutes les valeurs binaires de la table de transition sont obtenues. Les valeurs binaires indiquées dans le tableau de transition représentent les variables d'excitation Y1 et Y2.
Par exemple, la première ligne et la première colonne de la table de transition contiennent la valeur binaire 00, donc Y1Y2 = 00.
De même, Y1Y2 = 01 dans la première ligne et la deuxième colonne du tableau de transition, Y1Y2 = 11 dans la deuxième ligne et la première colonne du tableau de transition, etc.
Dans le tableau de transition, les entrées qui ont des variables d'excitation Y1Y2 = variables secondaires y1y2 sont en gras pour indiquer une condition d'état stable.
Par exemple, la première ligne de la première colonne du tableau de transition a des variables d'excitation Y1Y2 = 00.
Les variables secondaires y1y2 = 00 correspondent à la première ligne de la première colonne du tableau de transition.
Ainsi, Y1Y2 = y1y2 = 00 (tableau de transition première ligne, première colonne).
De même, Y1Y2 = y1y2 = 01 (tableau de transition deuxième, ligne deuxième colonne).
Y1Y2 = y1y2 = 11 (Troisième ligne, première colonne du tableau de transition).
Y1Y2 = y1y2 = 10 (tableau de transition de la quatrième rangée et de la deuxième colonne).
Dans le tableau de transition, toutes les entrées en gras affichent un état stable et les autres entrées affichent un état instable.
Les quatre états stables en transition sont les suivants :
y1y2x = 000, 011, 110 et 101
Les quatre états instables du tableau de transition sont :
y1y2x = 001, 010, 111 et 100.
Le table d'état est présenté dans le tableau ci-dessous:
Tableau d'état
|
Variables d'entrée secondaires |
Variables d'excitation (État suivant) | ||||
| État actuel | Pour x = 0 | Pour x = 1 | |||
| y1 | y2 | Y1 | Y2 | Y1 | Y2 |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 |
La table d'état est obtenue à partir de la tableau de transition.
Voir la figure ci-dessous pour la définition des variables d'entrée secondaires et des variables d'excitation.
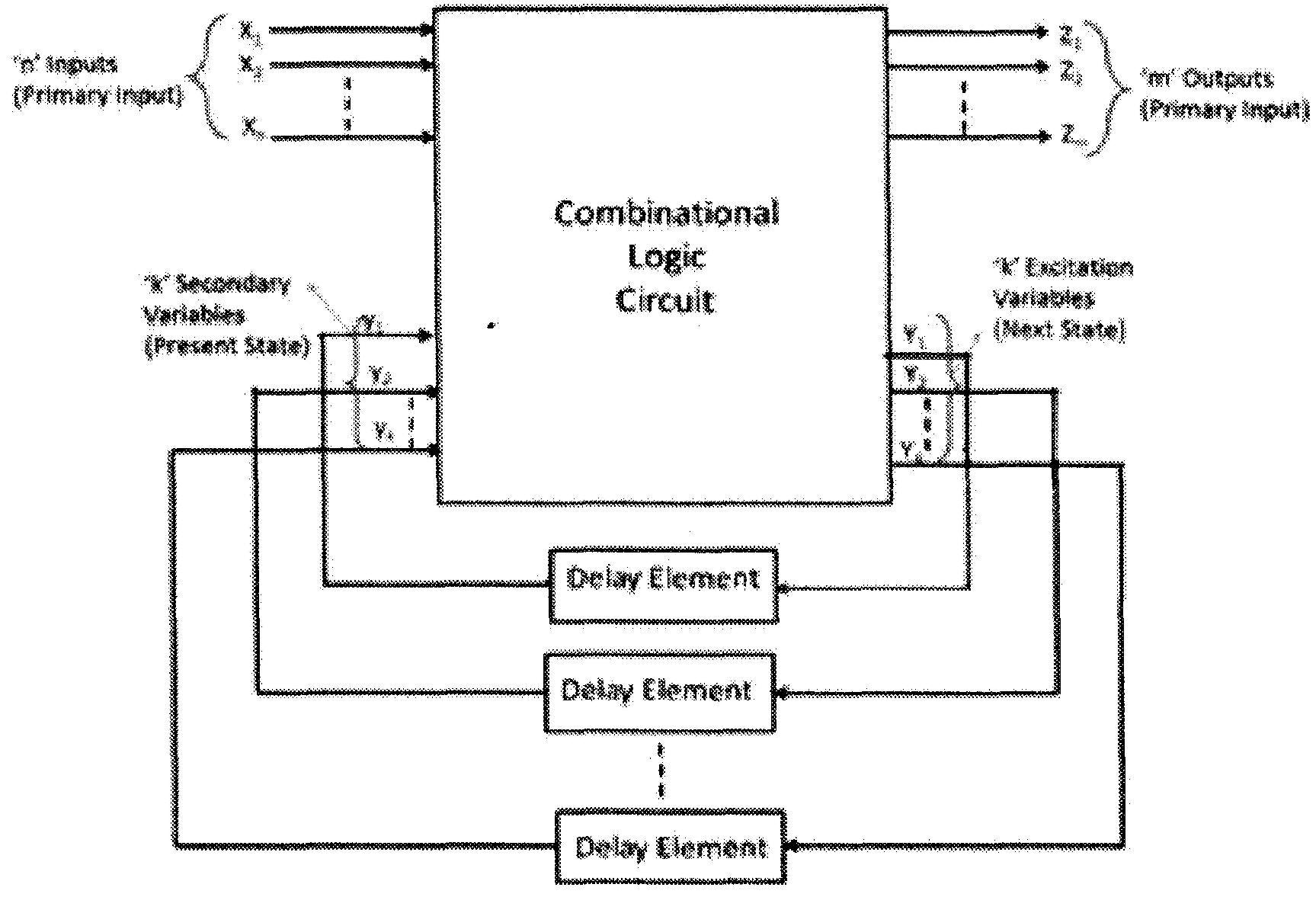
Table de flux
La table de flux est très similaire à la table de transition, à l'exception d'une petite différence.
Dans la table de transition, les états internes sont représentés par des valeurs binaires tandis que dans la table de flux, les états sont représentés par une lettre (a, b, c... ou x, y, ... etc).
Nous savons que dans la table de transition, chaque ligne représente un état.
Considérons à nouveau la table de transition ci-haut.
La première ligne (premier état) a la valeur binaire 00, la deuxième ligne (deuxième état) a la valeur binaire 01, la troisième ligne (troisième état) a la valeur binaire 11 et la quatrième ligne (quatrième état) a la valeur binaire 10.
Pour construire une table de flux nous attribuerons une lettre à chacun de ces états.
Soit a = 00, b = 01, c = 11 et d = 10.
Le tableau de flux est présenté à la figure ci-dessous:
| x | |||
| x'(0) | x(1) | ||
| y | a | a | b |
| b | c | b | |
| c | c | d | |
| d | a | d | |
Aussi y = y1y2 avec y1y2 = 00 à 11.
Le tableau de flux de la figure contient :
• 4 états : a, b, c et d.
• Une entrée principale x.
• Et 4 états stables.
La table de flux qui n'a qu'un seul état stable dans chaque ligne est une table de flux primitive.
Étant donné que la table de flux illustrée dans le tableau a un état stable dans chaque ligne, il s'agit d'une table de flux primitive.
Le tableau ci-dessous montre un autre tableau de flux.
| x1x2 | ||||||
| C1 | C2 | C3 | C4 | |||
| 00 | 01 | 11 | 10 | |||
| y | R1 | a (0) | a,0 | a,0 | a,0 | b,0 |
| R2 | b (1) | a,0 | a,0 | b,1 | b,0 | |
Ce tableau de flux contient :
• 2 états : a et b.
• Deux entrées primaires X1 et x2.
• Une sortie x. La valeur binaire de la sortie x est écrite avec le nom de l'état séparé par une virgule. Par exemple, a, 0 dans la première ligne de la première colonne, b, 1 dans la deuxième ligne de la troisième colonne et ainsi de suite.
• 5 états stables.
À partir du tableau de flux de la figure 5.3(b), on peut noter que :
Si x1 = 0, le circuit est dans l'état 'a'.
Le x1 = 0 dans la première ligne, première colonne (R1C1), la première ligne, deuxième colonne (R1C2), la deuxième ligne, première colonne (R2C1) et dans la deuxième ligne, deuxième colonne (R2C2).
Si x1 = 1 et x2 = 0, le circuit est dans l'état 'b' .
Le x1x2 = 10 dans la première rangée, quatrième colonne (R1C4) et dans la deuxième rangée, quatrième colonne (R2C4).
Si x1 = 1 et x2 = 1, le circuit peut être dans l'état 'a' ou dans l'état 'b'.
Le x1 x2 = 11 et = 1 dans la troisième colonne de la première rangée (R1C3) et dans la troisième colonne de la deuxième rangée (R2C3).
Noter que:
L'état 'b' est maintenu si l'entrée x1x2 passe de 10 à 11.
L'état 'a' est maintenu si l'entrée x1x2 passe de 01 à 11.
Supposons maintenant que nous souhaitions concevoir un diagramme logique à partir d’une table de flux donnée.
Faire cela:
1.Tout d’abord, le nom de l’état dans l’organigramme se verra attribuer des valeurs binaires. Ceci est fait de manière à convertir la table de flux donnée en table de transition.
Les valeurs indiquées dans le tableau de transition sont Y. À l'aide du tableau de transition, nous obtiendrons la valeur de la variable d'excitation « Y ».
2. Deuxièmement, la K-Map pour la sortie z est construit.
La valeur binaire de la sortie « z » est indiquée dans le tableau de flux à côté de chaque nom d'état séparé par une virgule.
À l'aide de cette valeur binaire, K-Map est dessiné.
3. Troisièmement, à l'aide de la table de transition et de K-Map, le schéma logique est dessiné.
Ceci est illustré par l’exemple suivant :
Reprenons l'exemple de tableau de flux ci-haut.
1. Tout d’abord, le nom de l’état dans l’organigramme se verra attribuer des valeurs binaires.
Supposons que l'état « a » reçoive la valeur binaire « 0 » et que l'état « b » reçoive la valeur binaire « 1 ».
La table de transition pour la table de flux du tableau ci-haut est celle illustrée dans le tableau ci-dessous:
| x1x2 | |||||
| 00 | 01 | 11 | 10 | ||
| y | y' (0) | 0 | 0 | 0 | 0 |
| Y (1) | 0 | 0 | 1 | 0 | |
La valeur indiquée dans le tableau de transition est Y.
La valeur binaire de Y = 1 pour l'état « b » et Y = 0 pour l'état « a ».
La table de transition est simplifiée pour obtenir Y = x1x2' + x1y.
La table de transition est simplifiée de la même manière que nous simplifions K-Map.
Certaines valeurs de Y en gras montrent un état stable.
2. La valeur binaire de la sortie z est écrite à côté de chaque nom d'état séparé par une virgule dans le tableau de flux.
| x1x2 | ||||||
| C1 | C2 | C3 | C4 | |||
| 00 | 01 | 11 | 10 | |||
| y | R1 | a (0) | a,0 | a,0 | a,0 | b,0 |
| R2 | b (1) | a,0 | a,0 | b,1 | b,0 | |
Par exemple, la valeur binaire de la sortie z est « 0 » dans la première colonne de la première ligne (R1C1), la valeur binaire de z est « 0 » dans la quatrième colonne de la première ligne (R1C4), la valeur binaire de z est « 1 » dans la seconde ligne troisième Colonne (R2C3) et ainsi de suite.
Le K-Map pour la sortie z est illustrée à la figure ci-dessous:
| x1x2 | |||||
| x1'x2' | x1'x2 | x1x2 | x1x2' | ||
| 00 | 01 | 11 | 10 | ||
| y | y' (0) | 0 | 0 | 0 | 0 |
| Y (1) | 0 | 0 | 1 | 0 | |
z = x1x2y.
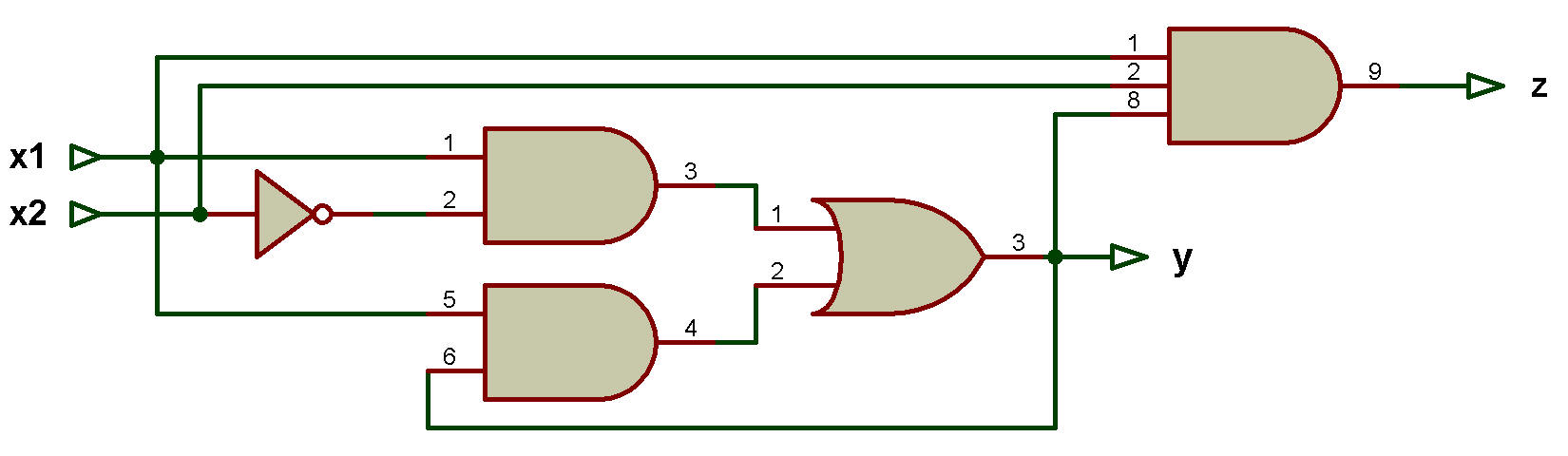
3. Le schéma logique est présenté dans la figure ci-dessous: