Procédure de conception
Logique séquentielle asynchrone
La procédure de conception d'un circuit séquentiel asynchrone commence par l'énoncé du problème. Une fois l’énoncé du problème connu, diverses étapes de conception sont suivies, ce qui conduit finalement à un diagramme logique.
Ce schéma logique obtenu décrit le fonctionnement du circuit selon l'énoncé du problème donné.
Fondamentalement, les étapes suivies lors de la procédure de conception sont :
1. Un tableau de flux primitif est obtenu à partir de l’énoncé du problème. Une table de flux primitive est une table de flux qui n'a qu'un seul état stable dans chaque ligne.
2. La table de flux est ensuite réduite à un nombre minimum d'états.
3. Ensuite, les états reçoivent une valeur binaire à partir de laquelle nous obtenons la table de transition.
4. Enfin, à partir de la table de transition, le schéma logique est obtenu. Ce schéma logique est soit un circuit combinatoire avec rétroaction, soit un circuit avec des verrous SR.
Comprenons la procédure de conception avec un exemple.
Exemple de procédure de conception :
L'énoncé du problème donné indique de concevoir un circuit de verrouillage à porte ayant :
Deux entrées : G (porte) et D (données) Et une sortie : Q
La condition est la suivante :
Lorsque G = 1, les données binaires présentes à l'entrée D sont transférées telles quelles vers la sortie Q.
Cela signifie que si G = 1 et D = 1 alors les données en « D », c'est-à-dire « 1 » seront transférées vers Q de sorte que Q = D = 1 et si G = 1 et D = 0 alors les données en « D », c'est-à-dire que « 0 » sera transféré à Q de sorte que Q = D = 0.
Lorsque G = 0, alors tout changement de valeur binaire de l'entrée D n'est pas transféré à Q.
Cela signifie que tant que G = 0, la sortie Q continue de maintenir sa valeur binaire actuelle malgré les changements de valeur binaire de D.
Les étapes de conception suivies sont désormais :
1. La première étape consiste à obtenir une table de flux primitive.
Pour obtenir le tableau de flux primitif, nous allons d'abord dessiner un tableau d'états totaux pour montrer tous les états possibles pour les combinaisons d'entrée D et G données.
Ce tableau est présenté dans le tableau ci-dessous:
| État | Entrées | Sorties | Remarques | ||
| D | G | Q | |||
| Condition 1 | a | 0 | 1 | 0 | G=1, Donc Q=D=0 |
| Condition 2 | b | 1 | 1 | 1 | G=1, Donc Q=D=1 |
| Condition 3 | a | 0 | 1 | 0 | G=1, Donc Q=D=0 |
| c | 0 | 0 | 0 | Après l'état « a », G
devient 0. Donc Q maintient sa valeur binaire « 0 » comme il l'était dans l'état « a ». |
|
| Condition 4 | c | 0 | 0 | 0 | G=0 |
| d | 1 | 0 | 0 | Après l'état 'c', 6= 0 mais
D devient 1. Puisque G = 0, donc Q conserve sa valeur binaire '0' comme il l'était dans l'état 'c' |
|
| c | 0 | 0 | 0 | Après l'état 'd', G= 0 mais
D redevient 0 à partir de X. Puisque G = 0, donc Q maintient sa valeur binaire '0' telle qu'elle était dans l'état d' |
|
| Condition 5 | b | 1 | 1 | 1 | G=1, Donc Q=D=1 |
| e | 1 | 0 | 1 | Après l'état 'b', G devient
0. Donc Q conserve sa valeur binaire 1 telle qu'elle était dans l'état 'b' |
|
| Condition 6 | e | 1 | 0 | 1 | G=0 |
| f | 0 | 0 | 1 | Après l'état 'e', G= 0
mais D devient impair à partir de 1. Puisque G = 0, donc Q conserve sa valeur binaire 1 telle qu'elle était dans l'état 'e' |
|
| e | 1 | 0 | 1 | Après l'état 'f, G= 0 mais
D redevient 1 à partir de 0. Puisque G =0, donc Q maintient sa valeur binaire 1 telle qu'elle était dans l'état 'f |
|
Dans le tableau, il y a au total 6 états possibles auxquels sont attribuées des lettres : a, b, c, d, e et f.
Notez que : les variables d'entrée DG ne peuvent pas changer de DG = 01 à 10 ou DG = 00 à 11, cela signifie que D et G ne peuvent pas changer en même temps (dans la même transition).
C'est pourquoi le tableau ne comporte pas cette transition (DG = 01 à 10 ou DG = 00 à 11).
À l'aide de ce tableau, nous dessinerons une table de flux primitive.
Le tableau de flux primitif est illustré ci-dessous:
| 00 | 01 | 11 | 10 | |
| a | c,- | a,0 | b,1 | -,- |
| b | -,- | a,- | b,1 | e,- |
| c | c,0 | a,- | -,- | d,- |
| d | c,- | -,- | b,- | d,0 |
| e | f,- | -,- | b,- | e,1 |
| f | f,1 | a,- | -,- | e,- |
Les étapes pour dessiner une table de flux primitive sont les suivantes :
i. Les lignes représentent l'état et les colonnes représentent une combinaison d'entrée possible.
Il y a donc 6 lignes pour six états : a, b, c, d, e et f ; et 4 colonnes pour une combinaison d'entrée possible de DG :
DG = 00, DG=01, DG=10 et DG = 11
ii. Maintenant, pour chaque état (a, b, ..., f représenté par la ligne du tableau de flux primitif), nous verrons le tableau pour toutes les combinaisons d'entrées DG (DG = 00 à DG = 11) où il existe un état stable et puis correspondant à cette combinaison d'entrée DG, nous ferons une entrée.
L'entrée contiendra le nom de l'état et la valeur binaire de la sortie Q séparés par une virgule.
Par exemple, commencez par l’état « a ».
L'état « a » est stable pour DG = 01 (voir tableau, première ligne).
Ainsi, sur le tableau de flux primitif, nous ferons l'entrée a,0 dans la ligne 1 colonne 2 (la colonne 2 correspond à DG = 01).
L'entrée a, 0 indique l'état « a » et « 0 » est la valeur binaire de la sortie Q.
De même, l'état « b » est stable pour DG = 11 (voir tableau, deuxième ligne).
Ainsi, dans le tableau de flux primitif, nous ferons l'entrée b,1 dans la ligne 2 colonne 3 (la colonne 3 correspond à DG =11).
L'entrée b,1 indique l'état « b » et « 1 » est la valeur binaire de la sortie Q.
De même, les entrées pour les états c, d, e et le tarif sont effectuées dans le tableau de flux primitif.
iii. Ensuite, nous savons que les variables d'entrée D et G ne peuvent pas changer en même temps (dans la même transition).
Cela signifie que DG ne peut pas passer de DG = 01 à 10 ou DG = 00 à 11.
Maintenant, pour chaque ligne (état), nous allons saisir deux tirets dans les colonnes qui diffèrent par deux variables ou plus des variables d'entrée associées au état stable.
Par exemple, l'état « a » est stable pour DG = 01 et donc la variable d'entrée associée à cet état « a » est 01.
Puisque les variables d'entrée D et G ne peuvent pas changer en même temps, donc pour cet état, les variables d'entrée DG peuvent passez à 00 ou 11 car une seule variable D ou G est modifiée à la fois, mais DG ne peut pas passer à 10 car D et G sont modifiés.
Ainsi, deux tirets sont inscrits dans la ligne 1 (état a) colonne 4 (DG = 10 dans la colonne 4) (voir Figure le tableau de flux primitif).
De même, une entrée pour les états b, c, d, e et f est effectuée dans le tableau de flux primitif.
iv. Nous allons maintenant remplir les deux colonnes restantes (combinaison DG d'entrée) correspondant à chaque ligne (état).
Nous le remplirons à l'aide des conditions et remarques indiquées dans le tableau pour chaque État.
Par exemple, l'état « c » peut venir après l'état « a » comme indiqué dans la condition 3 du tableau ou peut venir après l'état « d » comme indiqué dans la condition 4 du tableau.
Ainsi, la ligne 3 (état c), la colonne 2 (DG = 01) est marquée par 'a,-' et la ligne 3 (état c) la colonne 4 (DG = 10) est marquée par 'd,-' , '-' représente je m'en fiche et peut être 0 ou 1.
De même, l'état « e » peut venir après l'état « b » comme indiqué dans la condition 5 du tableau ou peut venir après l'état « f » comme indiqué dans la condition 6 du tableau.
Ainsi, la ligne 5 (état e), la colonne 1 (DG = 00) est marquée par « f,- » et la ligne 5 (état e), la colonne 3 (DG = 11) est marquée par « b,- ».
De la même manière, la valeur pour les autres états est déterminée.
2. La deuxième étape de la procédure de conception est la réduction de la table de flux primitive au nombre minimum d'états.
Nous savons que la table de flux primitive n'a qu'un seul état stable dans chaque ligne. La table de flux peut avoir un nombre réduit de lignes si deux états stables ou plus sont placés dans la même ligne.
Le regroupement d’états stables de différentes lignes en une seule ligne commune est appelé fusion.
Notez que : les colonnes ne peuvent pas être réduites car les colonnes représentent une combinaison d'entrée possible de DG.
La combinaison d'entrée possible restera la même avec DG = 00 à 11.
Notez également que : '-' (tiret) dans la table de flux peut être utilisé pour représenter n'importe quel état et '-' peut être '0' ou '1' pour la sortie.
Pour comprendre comment fusionner deux lignes ou plus en une seule ligne, nous reviendrons à nouveau à notre tableau de flux primitif.
En voyant ce tableau de flux primitif, nous constatons que :
À partir de la première colonne :
Ligne 1 (état a) Colonne 1 est: c,-
Ligne 3 (état c) Colonne 1 est: c,0
Ligne 4 (état d) Colonne 1 est : c,-
Cela signifie que l'état a, c, d pour la colonne 1 (DG = 00) a le même état « c » et la sortie est soit « 0 » soit « - » (peu importe qui peut être 0 ou 1).
Passage à la deuxième colonne,
Ligne 1 (état a) La colonne 2 est : a,0
Ligne 3 (état c) la colonne 2 est : a,-
Ligne 4 (état d) La colonne 2 est : -,-
Cela signifie que l'état a, c, d pour la colonne 2 (DG = 01) a le même état « a » ou « - », « - » (tiret) peut être associé à n'importe quel état, et la sortie est soit 0, soit « - », « - » représente ne s'en soucie pas qui peut être 0 ou 1.
Passons à la troisième colonne,
Ligne 1 (état a) La colonne 3 est : b,-
Ligne 3 (état c) La colonne 3 est : -,-
Ligne 4 (état d) La colonne 3 est : b,-
Cela signifie que l'état a, c, d pour la colonne 3 (DG = 11) a le même état « b » ou « - » et la sortie est « - » (peu importe qui peut être 0 ou 1).
Passer à la dernière (quatrième) colonne,
Ligne 1 (état a) La colonne 3 est : -,-
Ligne 3 (état c) La colonne 3 est : d,-
Ligne 4 (état d) La colonne 3 est : d,0
Cela signifie que l'état a, c, d pour la colonne 4 (DG = 10) a le même état « d » ou « - » et la sortie est soit 0, soit « - » (peu importe qui peut être 0 ou 1).
Ainsi, les états a, c et d peuvent être fusionnés car après avoir fusionné ces 3 états, nous n'avons aucun conflit concernant les états ou la sortie.
De même, nous pouvons fusionner b, e et f (voir les lignes et colonnes pour b, e et f comme indiqué ci-dessus, procédure pour a, c et d).
Nous avons donc deux groupes : (a, c, d) et (b, e, f).
Le tableau ci-dessous montre le groupe -(a, c, d) et le groupe - (b, e, f).
| groupe -(a, c, d) | groupe - (b, e, f) | ||||||||
| DG | DG | ||||||||
| 00 | 01 | 11 | 10 | 00 | 01 | 11 | 10 | ||
| a | c,- | a,0 | b,- | -,- | b | -,- | a,- | b,1 | e,- |
| c | c,- | a,- | -,- | d,- | e | f,- | -,- | b,- | e,1 |
| d | c,- | -,- | b,- | d,0 | f | f,1 | a,- | -,- | e,- |
Maintenant, ces deux groupes, comme le montrent le tableau, peuvent être fusionnés comme suit :
La première colonne (DG = 00) du tableau montre l'état « c » dans les trois lignes et affiche un « 0 » ou un « - » (tiret).
Puisque « - » est une condition indifférente, il peut être associé à n’importe quel état ou sortie.
Ainsi, le « - » dans la première colonne de la première ligne et la première colonne de la troisième ligne est rendu « 0 » pour que les trois lignes soient identiques à « c,0 ».
Ceci est illustré dans la première ligne, première colonne du tableau ci-dessous:
| groupe -(a, c, d) | ||||
| DG | ||||
| 00 | 01 | 11 | 10 | |
| a,c,d | c,0 | a,0 | b,- | d,0 |
| b,e,f | f,1 | a,- | b,1 | c,1 |
De même, la deuxième colonne (DG = 01) du tableau affiche l'état « a » ou « - » dans les trois lignes et la sortie sous la forme « 0 » ou « - » (tiret).
Puisque « - » est une condition indifférente, il peut être associé à n’importe quel état ou sortie.
Ainsi, le « - » avant la virgule dans la première colonne de la troisième ligne est transformé en « a » et le « - » après la virgule est transformé en « 0 » pour que les trois lignes soient identiques à « a,0 ».
Ceci est illustré dans la première ligne, deuxième colonne du tableau ci-haut.
Les autres lignes et colonnes sont remplies de la même façon.
Le groupe - (a, c, d) comme indiqué dans la première rangée du tableau peut recevoir le nom d'état « a » et le groupe - (b, e, f) comme indiqué dans la deuxième rangée peut recevoir le nom d'état 'b'.
Le tableau de débit réduit de le tableau ci-haut peut être reconstruit comme le montre le tableau ci-dessous:
| DG | ||||
| 00 | 01 | 11 | 10 | |
| a | a,0 | a,0 | b,- | a,0 |
| b | b,1 | a,- | b,1 | b,1 |
3. La troisième étape de la procédure de conception consiste à attribuer une valeur binaire à chaque état afin que la table de transition puisse être dessinée.
Une fois que nous avons réduit le tableau de flux au nombre minimum d’états, nous allons maintenant attribuer des valeurs binaires aux états.
Le tableau de flux d'état réduit obtenu est présenté dans le tableau ci-haut.
Ici, nous donnons la valeur binaire « 0 » à l'état « a » et la valeur binaire « 1 » à l'état « b ».
À l'aide du tableau ci-haut, nous obtenons la table de transition comme le montre le tableau ci-dessous:
| DG | |||||
| 00 | 01 | 11 | 10 | ||
| Y | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | |
La table de transition du tableau B est dessinée comme décrit ci-dessous.
Le tableau de débit réduit comporte l'entrée « a, 0 » dans la première ligne, première colonne.
Ici, « a » est l'état et « 0 » est la valeur binaire de la sortie.
Ainsi, dans le tableau de transition, nous avons « 0 » dans la première ligne, première colonne car l'état « a » a la valeur binaire « 0 ».
De même, le tableau de débit réduit comporte l'entrée « b,- » dans la troisième colonne de la première rangée.
Ici, «b» est l'état et «-» (peu importe, peut être 0 ou 1) représente la sortie.
Ainsi, dans le tableau de transition, nous avons « 1 » dans la première ligne de la première colonne car l'état « b » a la valeur binaire « 0 ».
De même, les autres lignes et colonnes sont remplies dans le tableau de transition.
Notez que la table de transition n'a d'entrée que pour les états et n'a pas d'entrée pour les valeurs binaires de sortie, donc seules les valeurs binaires des états sont affichées dans la table de transition.
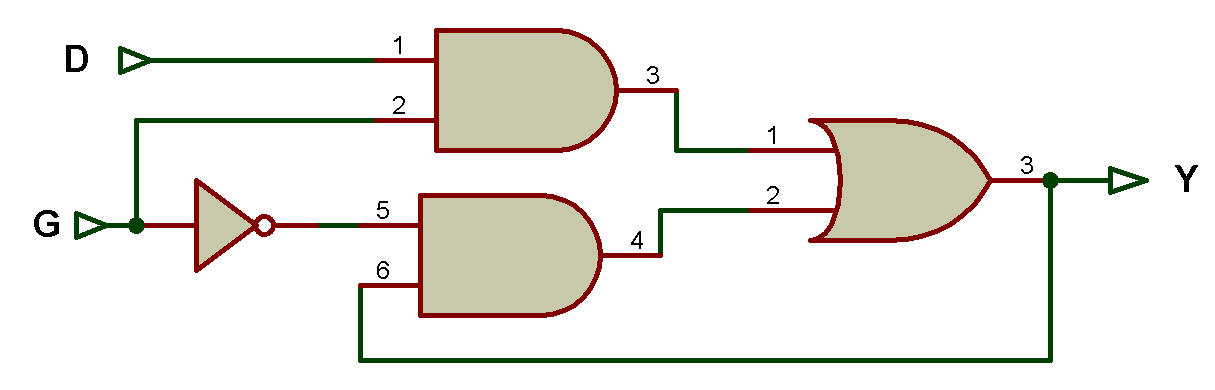
De la table de transition Y = DG + G¢y.
Nous allons maintenant attribuer des valeurs à « - » (peu importe) qui apparaissent après la virgule (comme « b,- » dans la première ligne, troisième colonne.
Puisque '-' représente peu importe, aucune valeur 0 ou 1 ne peut lui être attribuée.
Si nous attribuons des valeurs au '-' (peu importe) comme le montre le tableau ci-dessous, il est possible d'obtenir une sortie
Q = Y = DG + G'y
| DG | |||||
| 00 | 01 | 11 | 10 | ||
| Y | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | |
Si nous attribuons des valeurs au « - » (peu importe) comme le montre le tableau ci-dessous, il est possible d'obtenir une sortie Q = y.
| DG | |||||
| 00 | 01 | 11 | 10 | ||
| Y | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | |
4. La dernière étape de la procédure de conception consiste à construire un diagramme logique à partir de la table de transition.
Le diagramme logique peut être construit à l'aide de portes et le chemin de rétroaction est illustré à la figure ci-dessous en utilisant l'expression booléenne de Y obtenue à partir de la table de transition et l'expression booléenne de Q obtenue à partir du tableau ci-haut.

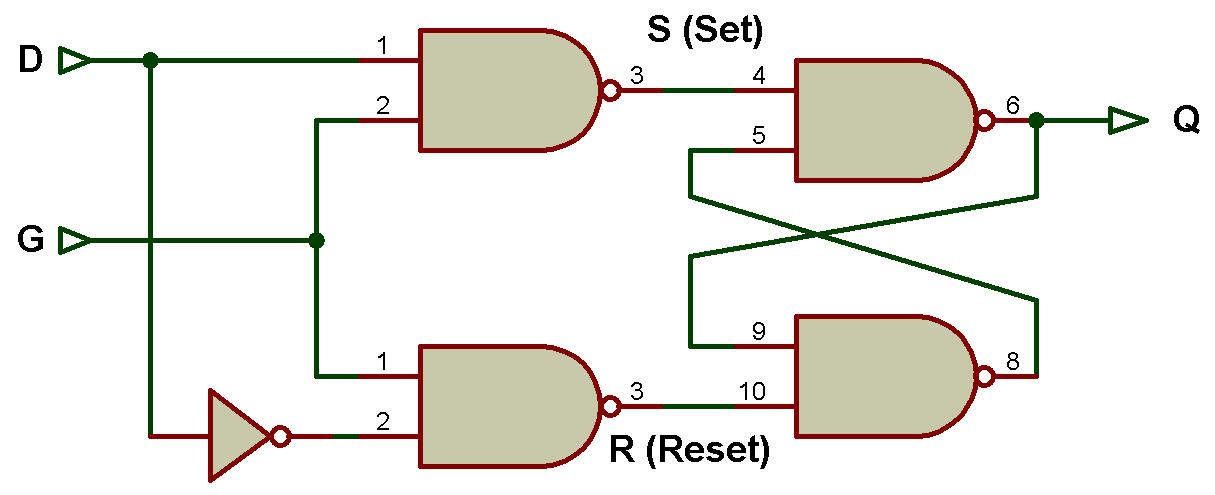
Le diagramme logique peut également être construit à l’aide du verrou SR.
Pour cela, dérivez d’abord la fonction booléenne pour S et R à l’aide de la table d’excitation SR Latch et de la table de transition donnée dans le tableau.
Le tableau d’excitation du verrou SR est présenté dans le tableau ci-dessous:
Y
État actuel
Y
État suivant
S
R
0
0
0
x
0
1
1
0
1
0
0
1
1
1
x
0
La procédure pour dériver la fonction booléenne pour S et R à l'aide de la table d'excitation du verrou SR et de la table de transition donnée est discutée dans la section Circuit avec Latch.
Les K-Maps pour S et R sont présentées respectivement dans le tableau ci-dessous:
| K-Map Pour S | K-Map Pour R | ||||||||
| DG | |||||||||
| 00 | 01 | 11 | 10 | 00 | 01 | 11 | 10 | ||
| Y | 0 | 0 | 0 | 1 | 0 | x | x | 0 | x |
| 1 | x | 0 | x | x | 0 | 1 | 0 | 0 | |
Le diagramme logique est présenté à la figure ci-dessous: