Réduction des tables d'état et de flux
Logique séquentielle asynchrone
La procédure de réduction d'état pour une table d'état donnée est effectuée à l'aide d'un algorithme qui combine deux états dans une table d'état en un seul s'ils sont équivalents.
Les deux états sont dits équivalents si :
"Pour chaque entrée possible, ils donnent exactement le même résultat et passent aux mêmes états suivants ou à des états suivants équivalents".
Il arrive souvent qu’une paire d’états n’aient pas les mêmes états suivants mais qu’ils passent à des états suivants équivalents.
Considérons le tableau d'état présenté dans le tableau ci-dessous:
| État actuel | État suivant | Sorties | ||
| x=0 | x=1 | x=0 | x=1 | |
| A | C | B | 0 | 1 |
| B | D | A | 0 | 1 |
| C | A | D | 1 | 0 |
| D | B | D | 1 | 0 |
Les états actuels A et B ont la même sortie pour la même entrée. Leurs états suivants pour X = 0 sont C et D, et les états suivants pour X = 1 sont B et A.
Si nous pouvons montrer que la paire d'états (C,D) sont équivalents, alors la paire d'états (A,B) seront également équivalents, car ils auront les états suivants identiques ou équivalents.
Lorsque cette relation existe on dit que (A,B) implique (C,D).
Cela signifie que si A et B sont équivalents alors C et D doivent être équivalents.
De même, les deux dernières lignes du tableau montrent que la paire d'états (C,D) implique la paire d'états (A,B).
Ainsi, la caractéristique des états équivalents est la suivante :
"Si (A,B) implique (C,D) et (C,D) implique (A,B), alors les deux paires d'états sont équivalentes"
Cela signifie que si A a les états suivants pour B sont équivalents, alors C et D le sont aussi.
Ainsi, les quatre lignes du tableau peuvent être réduites à deux lignes en combinant A et B dans un état, et C et D dans un deuxième état.
Afin de vérifier l'équivalence possible de chaque paire d'états avec d'autres états pour une table donnée, on peut le faire à l'aide d'une table d'implication.
Le tableau d’implication est en fait un graphique composé de carrés un pour chaque paire d’états possible.
À l’aide de cette table d’implication, on peut déterminer toutes les paires d’états équivalents.
Considérons le tableau d'état présenté dans le tableau ci-dessous:
| État actuel | État suivant | Sorties | ||
| x=0 | x=1 | x=0 | x=1 | |
| A | D | B | 0 | 0 |
| B | E | A | 0 | 0 |
| C | G | F | 0 | 1 |
| D | A | D | 1 | 0 |
| E | A | D | 1 | 0 |
| F | C | B | 0 | 0 |
| G | A | E | 1 | 0 |
Nous déterminerons toutes les paires d'états équivalents dans cet état dans le tableau à l'aide du tableau d'implication. La procédure pour ce faire est décrite ci-dessous.
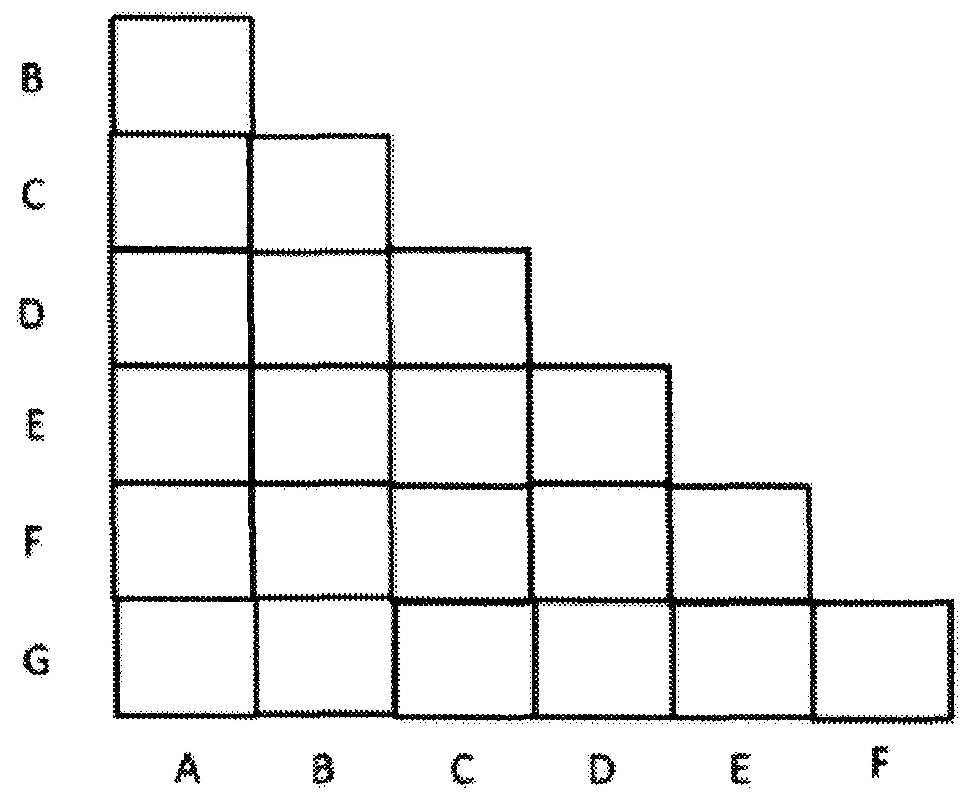
Tout d’abord, nous dressons un tableau d’implication.
Le tableau d'implication est présenté dans la figure ci-dessous:

Il y a 6 lignes et 6 colonnes. Les lignes montrent tous les états B à Q à l'exception du premier état A.
De même, les colonnes en bas montrent tous les états A à F, à l'exception du dernier état G.
Il y a 21 carrés affichés à l'intersection de la ligne et de la colonne. Ces carrés représentent toutes les combinaisons possibles de deux états quelconques.
Désormais, chaque carré affiché à l'intersection d'une ligne et d'une colonne pour les deux états sera testé pour son équivalence et sera rempli en conséquence.
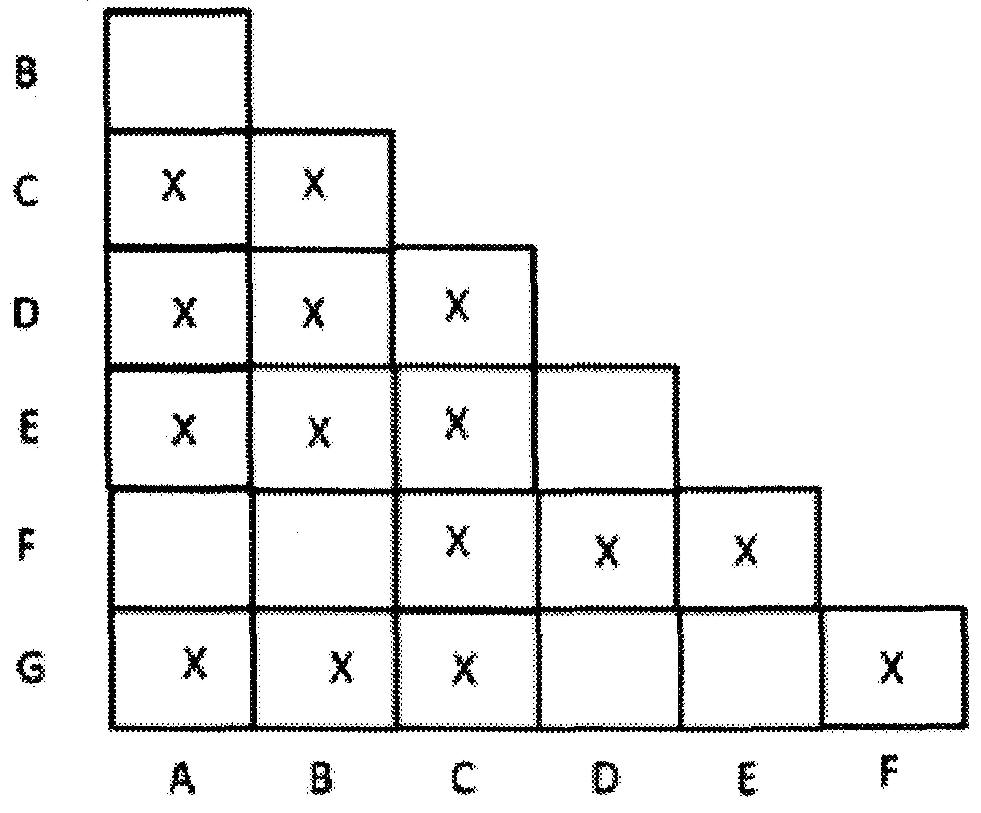
Les règles pour remplir la table de transition sont :
1. Marquez « X » dans tous les carrés correspondant à une paire d'états dont les sorties pour X = 0 et X = 1 ne sont pas égales aux sorties des autres états.
Dans notre état donné, selon le tableau, nous pouvons voir que :
• Les sorties de l'état C (pour X = 0 et X = 1) ne sont pas égales aux sorties des autres états. Marquez donc 'X' dans les lignes et colonnes correspondant à l'état C.
• Les sorties d'état D et A (pour X = 0 et X = 1) ne sont pas égales. Marquez donc 'X' dans le carré correspondant aux états D et A.
• Les sorties d'état D et B (pour X = 0 et X = 1) ne sont pas égales. Marquez donc 'X' dans le carré correspondant aux états D et B.
• De même, les autres paires d'états sont :
État E et A, État E et B, État F et D, État F et E, État G et A, État G et B, État G et F.
Marquez « X » dans le carré correspondant à toutes ces paires d'états.
Ceci est illustré dans la figure ci-dessous:
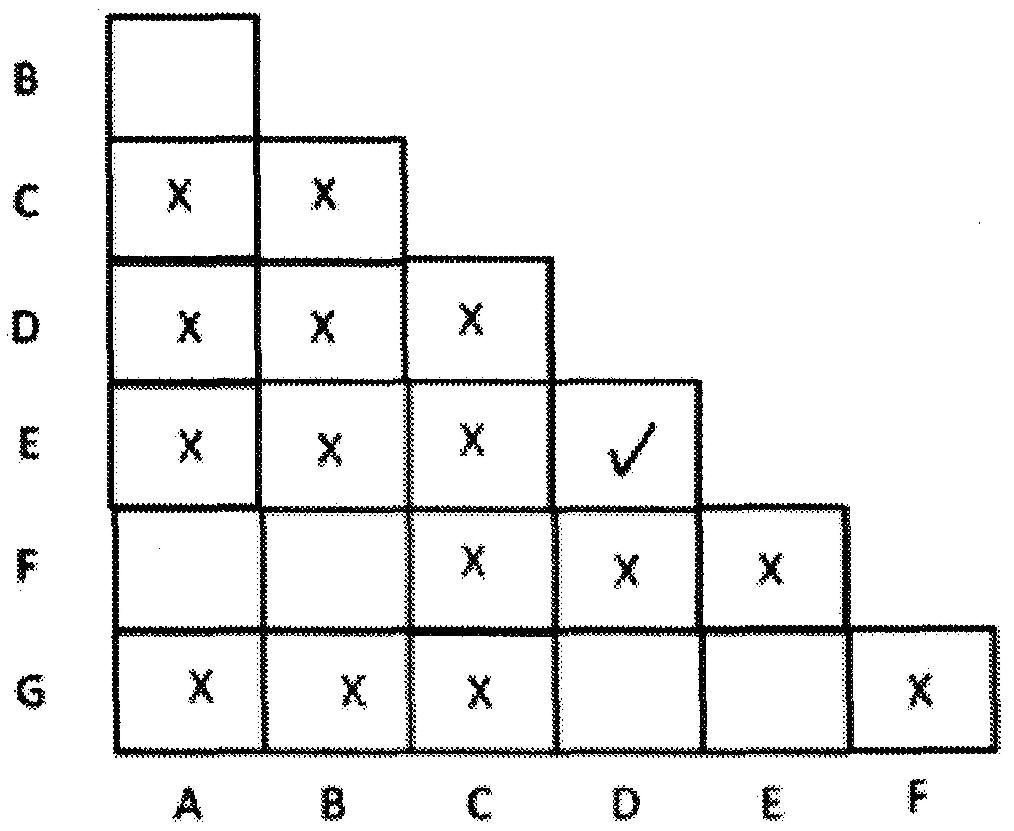
2. Marquez √ dans tous les carrés correspondant à une paire d’états équivalents.
Deux états sont équivalents si leurs états suivants sont identiques et que leurs sorties pour X = 0 et X = 1 sont égales.
Dans notre tableau d'états donné, nous pouvons voir que les états D, E sont équivalents. Marquez donc 'X' dans le carré correspondant à D et E.
Ceci est illustré dans la figure ci-dessous:
3. Nous allons maintenant remplir les carrés restants.
• En commençant par la paire A, B, nous avons l'état suivant D, E pour X = 0 et l'état suivant B, A pour X = 1.
Écrivez donc D,E dans le carré de la ligne B et de la colonne A. Marquez également comme la paire D,E a dans leur carré d'intersection correspondant.
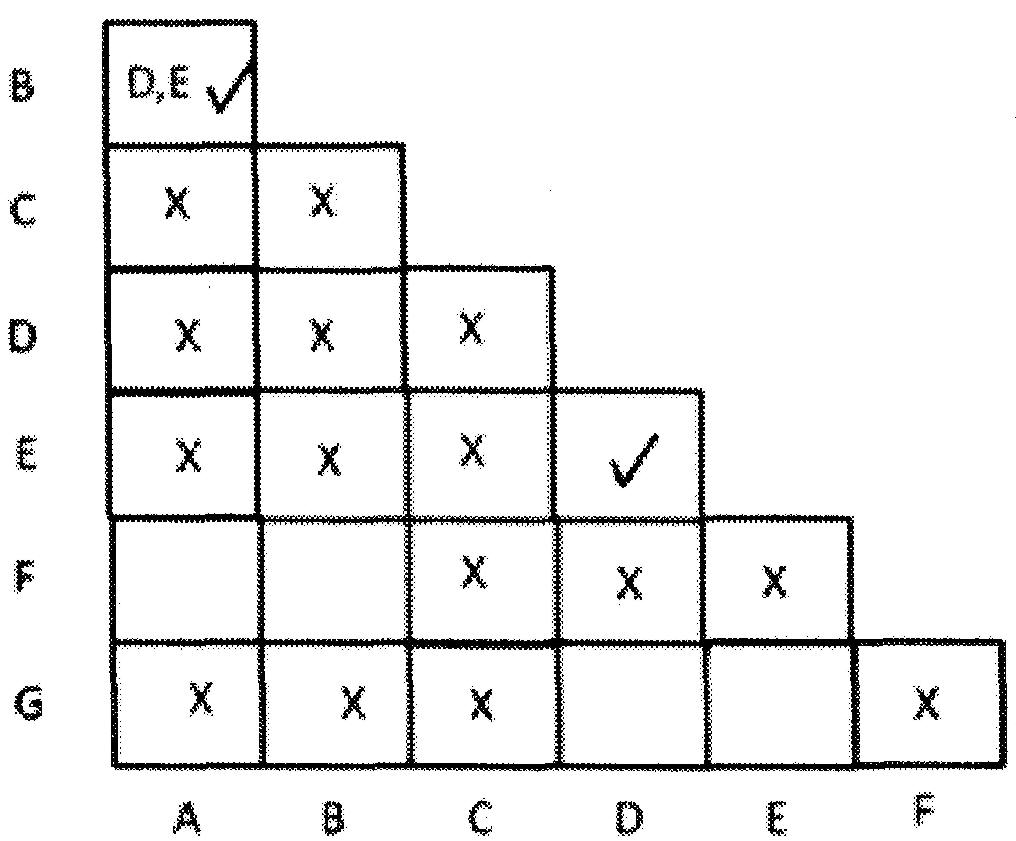
Pour la paire F,A nous avons le prochain état C,D pour X = 0 et le prochain état B,B pour X = 1.
Écrivez donc C,D au carré de la ligne F et la la colonne A.
Marquez également « X » comme paire D, E, un « X » dans leur carré d'intersection correspondant.
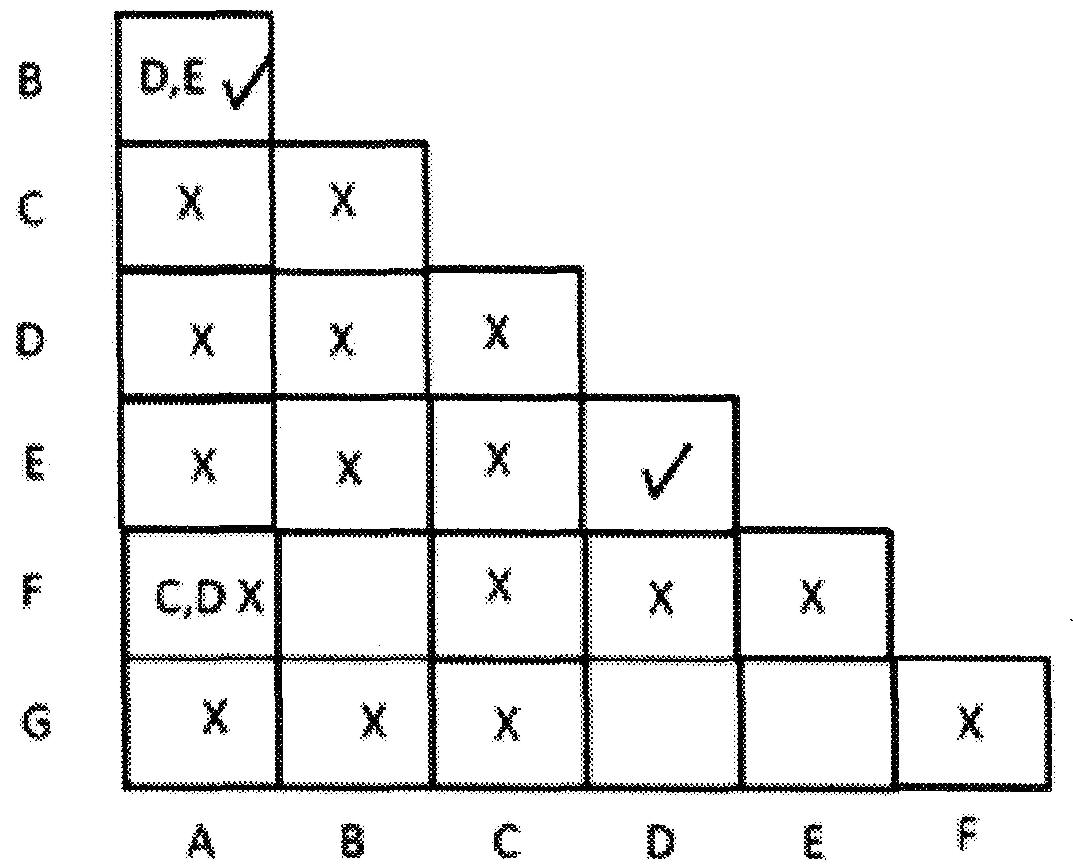
Pour la paire F,B nous avons le prochain état C,E pour X = 0 et le prochain état B,A pour X = 1.
Écrivez donc C,E et A,B au carré de la ligne F et de la colonne B . Marquez également « X » comme paire C,E, un « X » dans son carré d'intersection correspondant.
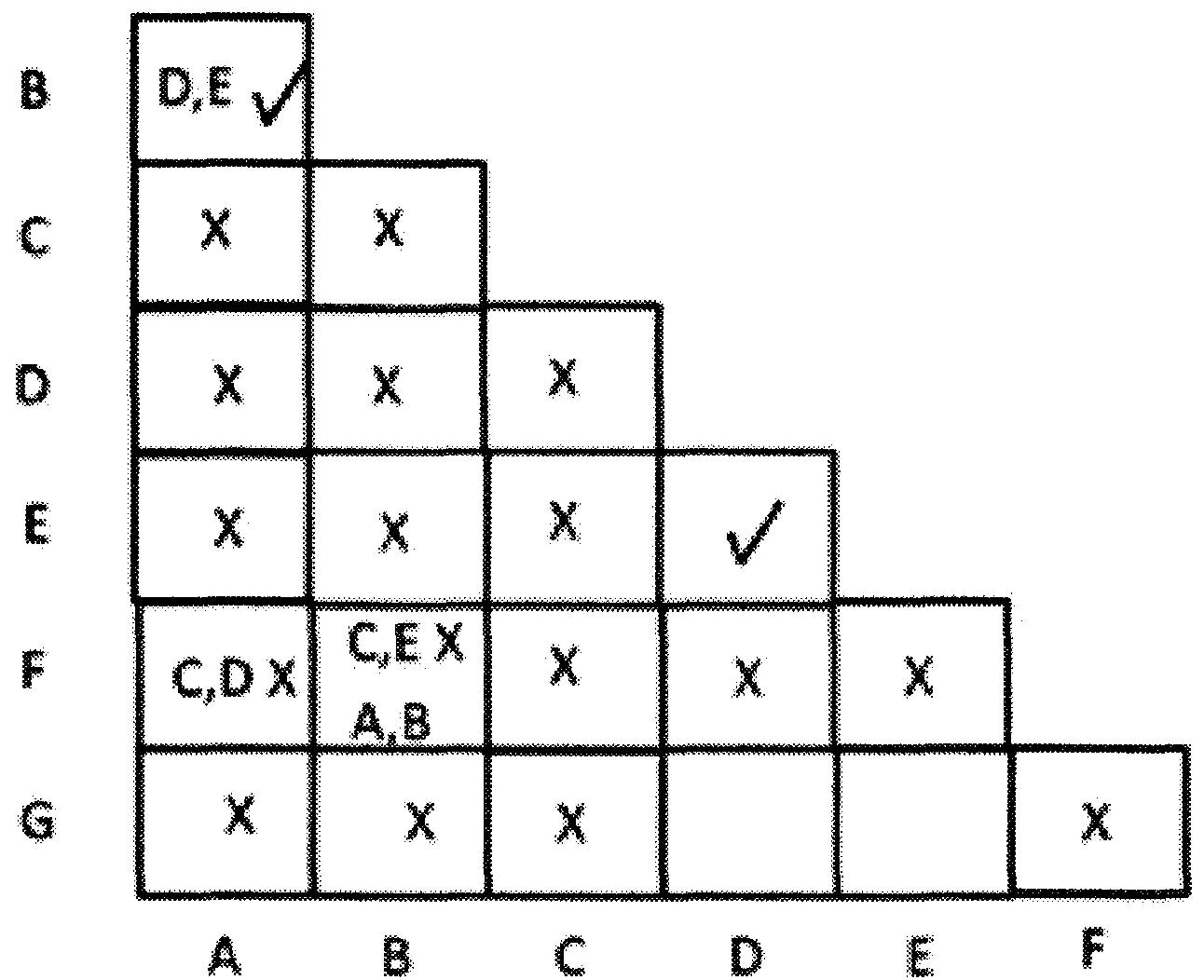
Pour la paire G,D nous avons l'état suivant A, A pour X = 0 et l'état suivant D,E pour X = 1.
Écrivez donc D,E au carré de la ligne G et de la colonne D . Marquez également comme la paire D,E, dans leur carré d'intersection correspondant.
Pour la paire G,E, nous avons l'état suivant A,A pour X = 0 et l'état suivant D,E pour X = 1.
Écrivez donc D,E dans la ligne G et le carré de la colonne E. Marquez également comme la paire D,E dans leur carré d'intersection correspondant
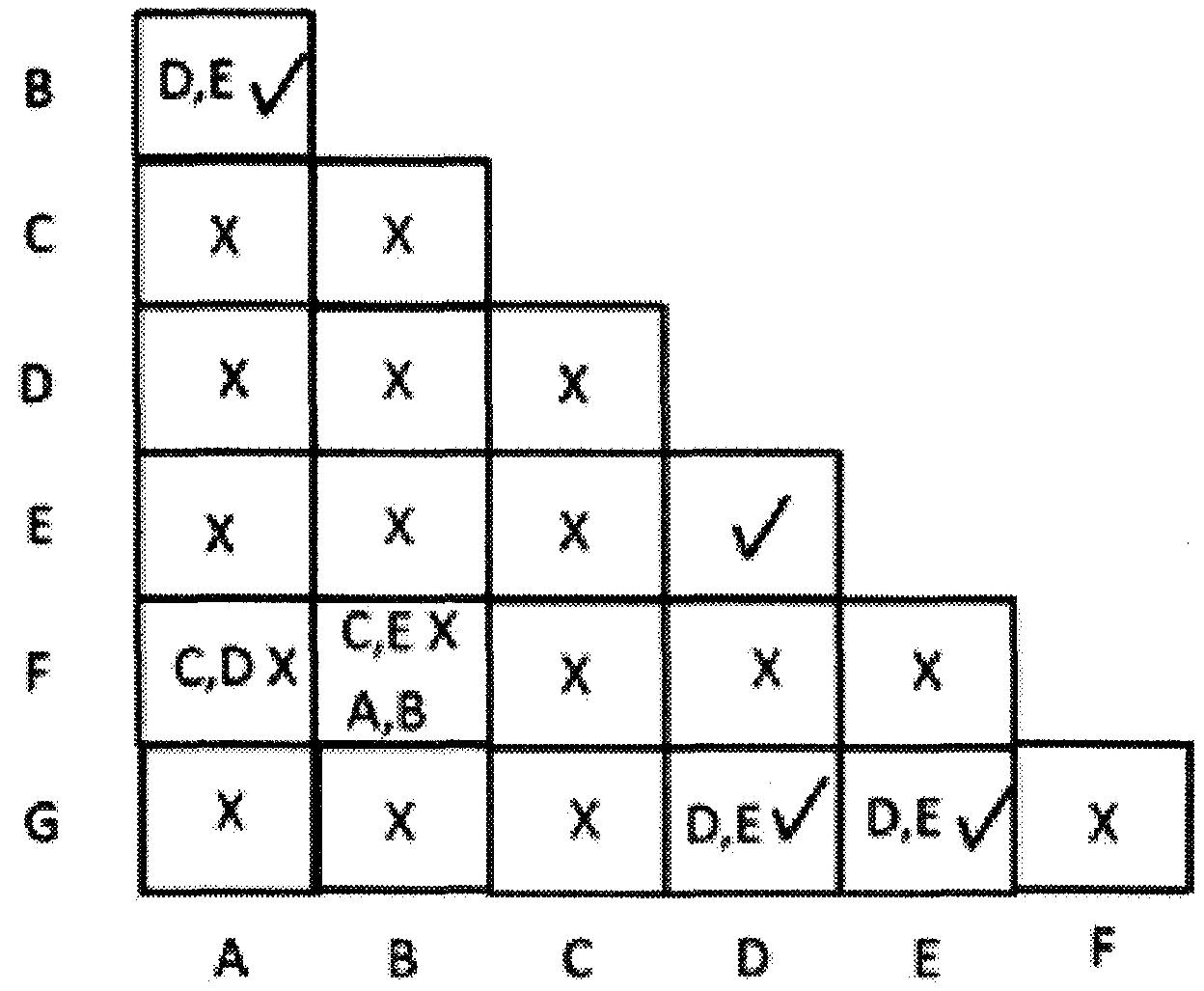
Ainsi, tous les carrés sont désormais remplis.
Tous les carrés qui ont √ montrent des paires d'états équivalents.
Dans la figure ci-haut Les états équivalents sont :
(A,B) (D,E) (D,G) (E,G)
Puisque D est équivalent à E, D est équivalent à G et G est équivalent à E, nous pouvons donc combiner les trois dernières paires pour former un groupe plus grand - (D,E,G).
Ainsi, le tableau peut être réduit de sept États à quatre États.
Ces quatre états sont : (A,B) (C) (D,E,G) (F).
Le tableau des états réduits est présenté dans le tableau ci-dessous.
Ce tableau est obtenu en remplaçant l'état B par A et les états E et G par D.
| État actuel | État suivant | Sorties | ||
| x=0 | x=1 | x=0 | x=1 | |
| A | D | A | 0 | 0 |
| B | D | F | 0 | 1 |
| D | A | D | 1 | 0 |
| F | C | A | 0 | 0 |
