Quelques machines complexes

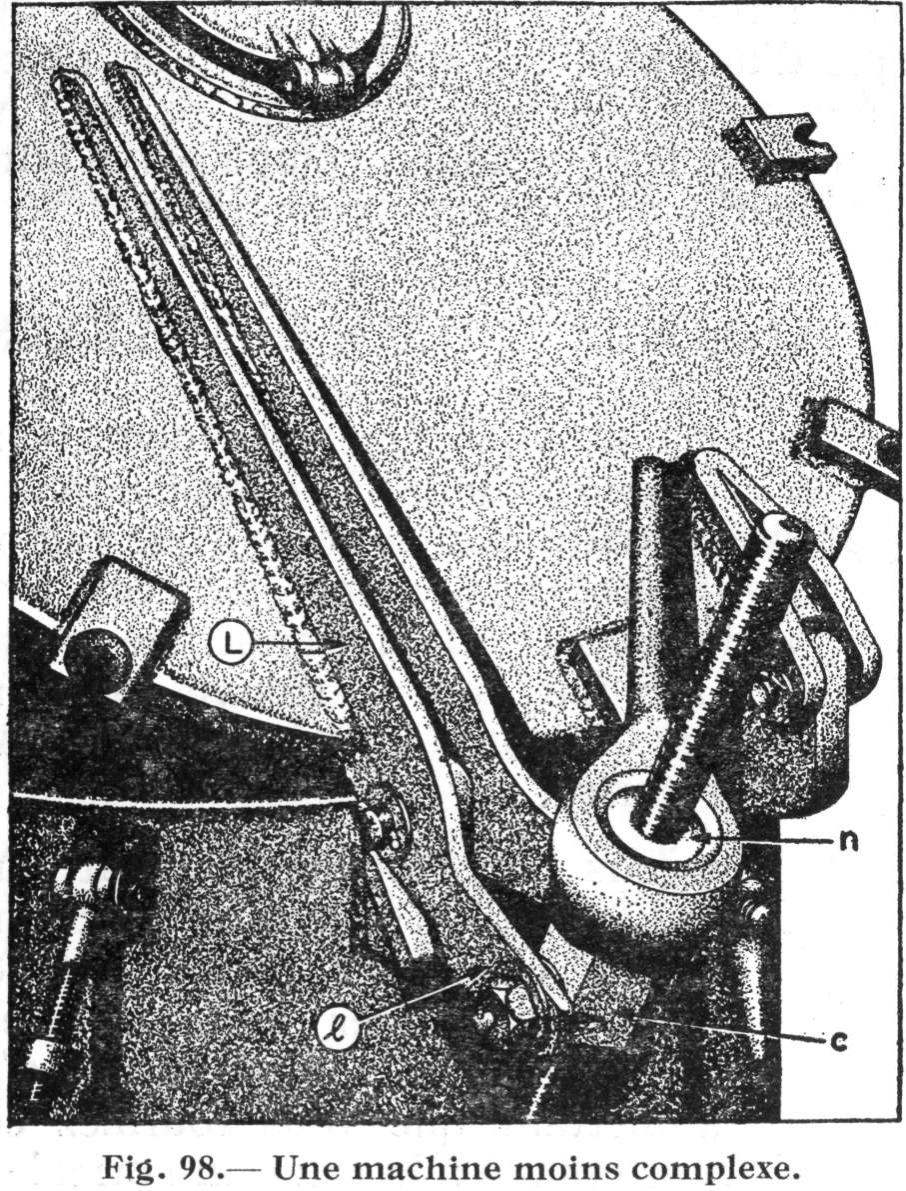
Voici une machine complexe dont le mécanisme est assez facile à comprendre. La trappe d'écoutille (hatch cover) que fait voir notre fig. 98 pèse une couple de cent livres. Le dispositif qui sert à l'ouvrir est une machine complexe. En fait, on y trouve deux machines simples qui sont: un vérin et un levier du premier genre.

Commençons par trouver le point où la force doit être appliquée pour faire fonctionner le dispositif. La clé à vis paraît bien être l'article. Il faut considérer toute clé de ce genre, on s'en souviendra, comme la raie d'une roue. En admettant que vous tourniez cette clé dans le sens opposé à la rotation normale des aiguilles d'une montre, vous dévisserez par le fait même l'écrou "n" qui s'élèvera de bas en haut sur le boulon fileté. Un tour complet de la clé fera monter l'écrou d'un pas de filet entier. Le collier "c" suivra l'écrou et fera monter le bras de levier "l", tandis que l'autre bras "L" du même levier s'abaissera en pivotant sur la charnière. Mais comme le bras "l" est beaucoup plus court que l'autre, le mouvement descendant de la trappe sera considérablement plus rapide que le mouvement ascendant du collier le long du boulon fileté. Nous avons affaire ici à un dispositif qui accélère le mouvement.

On ferme la trappe d'écoutille en tournant la clé à vis dans le sens contraire au mouvement des aiguilles d'une montre, mais on l'ouvre en procédant à l'inverse. Cette combinaison de deux machines simples est mécaniquement plus efficace qu'une machine unique.

Voici comment s'effectuent les calculs relatifs au fonctionnement d'une machine de ce genre. On commence par trouver le point où l'énergie est appliquée, puis on examine les organes de la machine qui y sont reliés. "C'est un vérin!" se dit-on, ou une roue mandrinée à son axe, ou encore une autre application d'une machine élémentaire.

"Si je fais tourner le vérin à droite, cette pièce va se déplacer dans tel sens. Par conséquent, le bras de levier s'en ira vers la droite. Et du fait que le levier est du premier genre, l'autre bras s'en ira vers la gauche".

A chaque étape, vous raisonnez de la même manière, en ayant soin de vous assurer du sens et de l'ampleur des mouvements.

Peut-être désirez-vous connaître l'intensité de la force qui s'exerce à un point quelconque de la machine, ou encore l'avantage mécanique obtenu à ce même point. Dans ce cas, il convient de ne pas oublier le principe que l'avantage mécanique que procure une machine complexe est égal au produit de l'avantage mécanique de chacune des machines simples dont elle est constituée.

Revenons au cas de notre trappe d'écoutille (fig. 98) et voyons un peu comment on peut en trouver les avantages mécaniques. Pour les besoins de la cause, admettons que la clé à vis du vérin est longue de 18 pouces à partir de son extrémité externe jusqu'au centre du boulon. Disons que le pas du filet a J de pouce. Le collier est fixé à l'extrémité du petit bras "l" à 5 pouces du point d'appui formé par la charnière, et le centre de la trappe se trouve à 18 pouces de cette même charnière, le long du bras "L".

L'avantage mécanique théorique du vérin peut se trouver en employant la formule:

Mais comme les vérins ont rarement une efficacité supérieure à 30 pour cent, il sera sage de réduire proportionnellement cet avantage mécanique théorique, soit 452 X 0.30 = 136.

Vous avez donc un avantage mécanique théorique de 136 à ce point de la machine.

Trouvons maintenant ce que le levier assure en fait d'avantage mécanique. L'avantage mécanique théorique d'un levier se calcule en divisant la longueur du bras de résistance par la longueur du bras où l'effort est appliqué.

L'avantage mécanique du levier est donc inférieur à 1. Chaque fois que pareille chose se présente, on sait que la vitesse ou la distance du mouvement a été accrue au détriment de la force. Dans le cas sous considération, on peut se permettre de sacrifier la force en faveur de la distance.

Ceci étant dit, revenons au calcul de l'avantage mécanique global de la machine. Cet avantage est égal au produit des deux avantages mécaniques, c'est-à-dire à 136 x 0.278 x 37.8.

Cet exemple fait voir de quelle manière il faut s'y prendre pour trouver l'avantage mécanique d'une machine complexe quelconque.

Recherche personnalisée