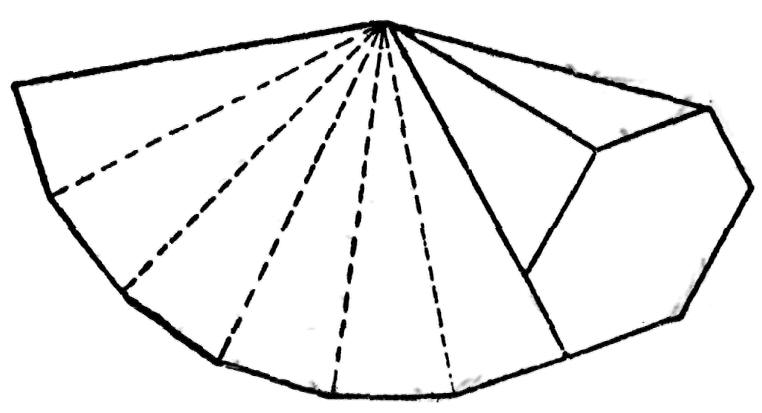
Fig. 182.— Déroulement d'une pyramide sur une surface plane.
Développement des pyramides et des cônes
Dessin et développement des tôles
Jusqu'ici, nous avons étudié des développements en traits parallèles. Le développement des surfaces pyramidales et coniques (radial development), c'est-à-dire qui convergent vers un point donné, présente une technique un peu différente.
Une pyramide est formée de parois planes qui lui assurent une base polygonale. Si elle a quatre parois placées à angle droit, c'est une pyramide régulière à base carrée; si elle a six côtés, c'est une pyramide régulière à base hexagonale, etc.
Le cône, par ailleurs, a une base circulaire; les cônes dont il sera question ici sont des cônes circulaires droits, c'est-à-dire dont le sommet (apex) se trouve placé directement au-dessus du centre de la base.
Pyramide droite
On peut illustrer la forme du patron développé d'une pyramide droite en tenant le sommet de cette pyramide sur un point fixe et en la déroulant comme fait voir notre fig. 182, de manière que les arêtes et les parois s'impriment sur la surface qui sert à l'expérience. Le patron qu'on obtient par ce procédé converge vers un point et tous les éléments en sont de longueur uniforme.

Fig. 182.— Déroulement d'une pyramide sur une surface plane.
La fig. 183 nous fait voir la méthode dite radiale dont on se sert pour développer une pyramide de ce genre. Les deux vues procurent une description des formes et dimensions. Tous les côtés sont numérotés de manière qu'ils puissent être identifiés sur les deux vues. On prend le sommet de la pyramide comme centre C et l'on décrit un arc AB de longueur indéterminée en prenant comme rayon l'une des arêtes extérieures de la pyramide.
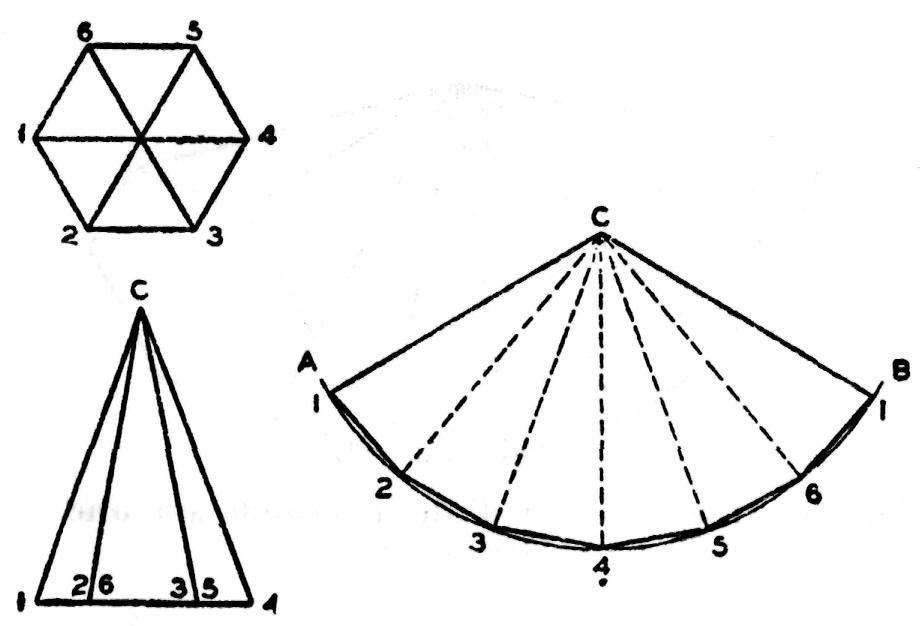
Fig. 183.— Développement d'une pyramide par la méthode dite radiale.
Bien que tous les côtés soient égaux, ils ne paraissent pas tels sur la vue de face ou élévation à cause de leur inclinaison. Il s'ensuit que seules les arêtes extérieures indiquent les vraies longueurs qui peuvent servir de rayon à l'arc.
On choisit un point sur cet arc comme premier élément et, à l'aide du compas, dont l'écartement est réglé d'après la largeur d'un côté de la base, les autres éléments sont reportés le long de l'arc. Les points ainsi repérés sont ensuite reliés par des traits droits pour former le contour du patron.
Des lignes sont tracées à partir de ces points vers le centre C afin d'indiquer où les plis devront être faits pour donner à l'objet sa forme réelle.
S'il s'agissait de développer une pyramide régulière à base carrée, on procéderait comme le montre notre fig. 184. Le développement Total se compose de la base carrée et de quatre triangles isocèles ayant pour base le côté C et pour côtés la longueur A de l'arête. L'arête ms, mv étant parallèle, la distance s'm' en donne la vraie grandeur.
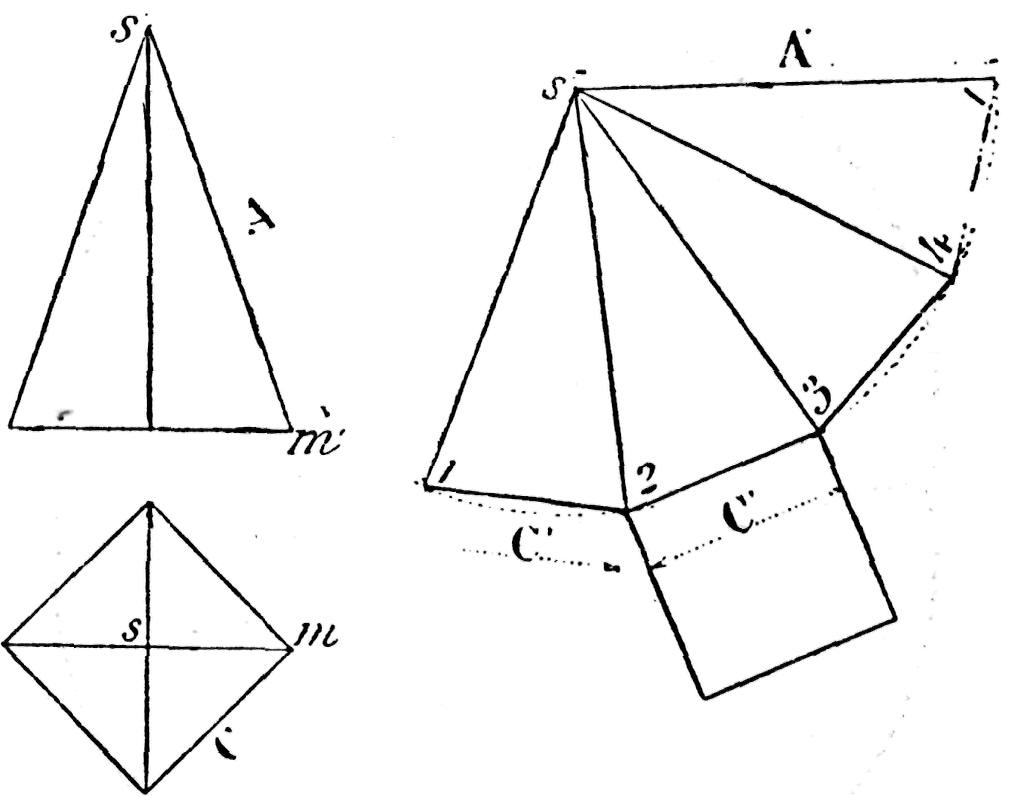
Fig. 184.— Développement d'une pyramide régulière à base carrée.
Le travail de développement proprement dit est identique à celui que nous venons de décrire pour la pyramide hexagonale, sauf que, pour former la représentation d'un solide, on construit le carré C en prenant pour l'un de ses côtés la base de l'un des triangles.
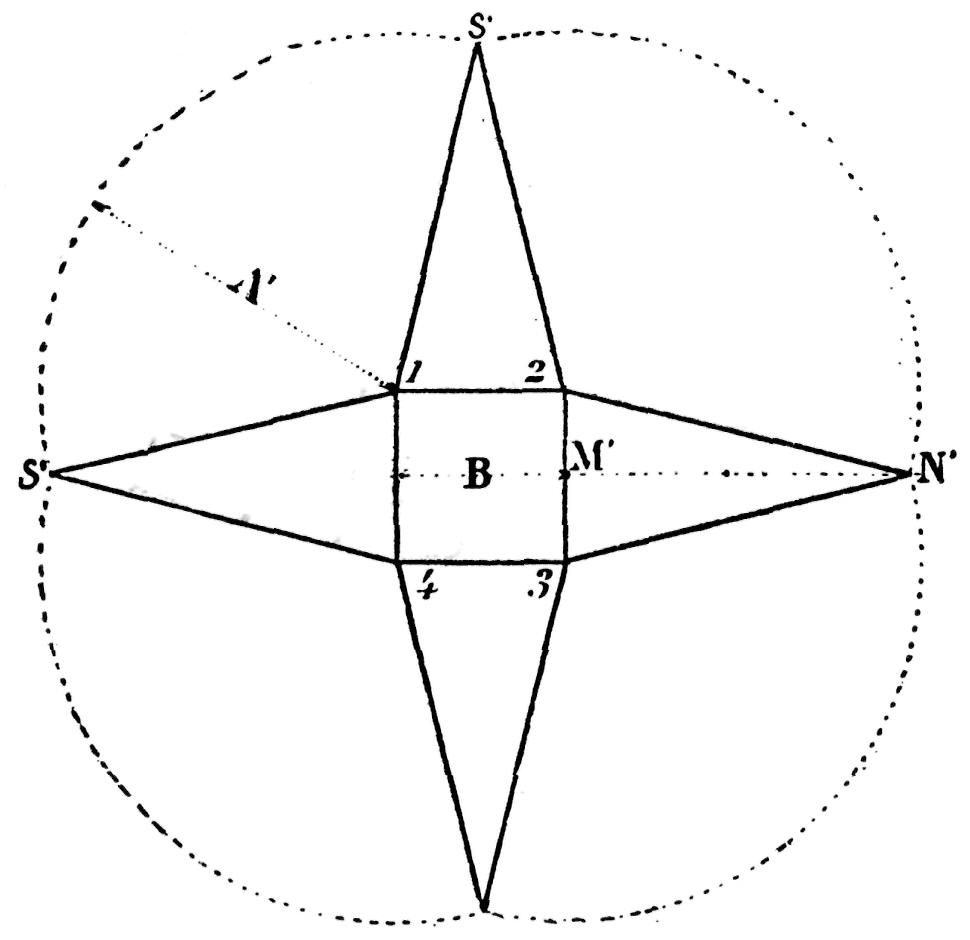
Fig. 185.— Disposition en étoile du développement d'une pyramide à base
carrée.
On pourrait tout aussi bien développer le solide d'une pyramide régulière à base carrée en disposant les quatre triangles non plus en éventail comme nous venons de le voir, mais plutôt en étoile (fig. 185). Dans ce cas, il faut pouvoir disposer d'une surface de papier beaucoup plus grande.
Après avoir construit la base B, on décrit à partir des points 1, 2, 3, 4, des arcs d'un rayon A' égal à l'arête latérale de la pyramide. Ces arcs déterminent les sommets des quatre triangles isocèles de la surface latérale.
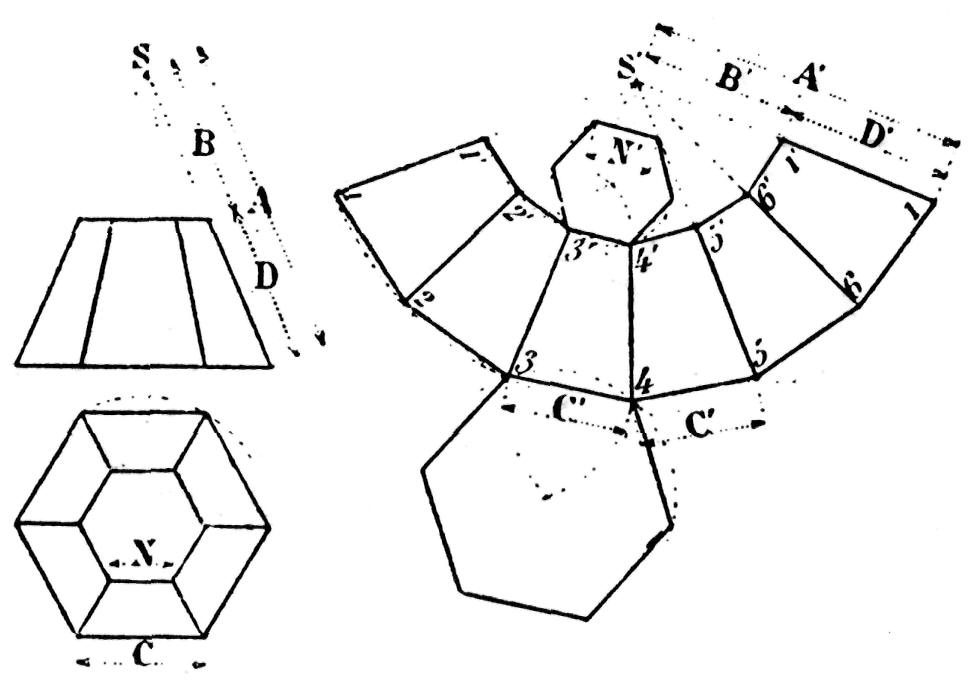
Fig. 186.— Développement du solide d'un tronc de pyramide régulière
hexagonale, à bases parallèles.
TRONC DE PYRAMIDE
Le développement des surfaces d'un tronc de pyramide (fig. 186) est identique à celui de la pyramide entière. Le développement du solide se compose de deux hexagones réguliers formant les bases et de six trapèzes symétriques formant les surfaces latérales.
Après avoir construit le développement de la pyramide comme si elle était entière (fig. 186), on décrit, du sommet S', un arc de rayon B' égal à B.
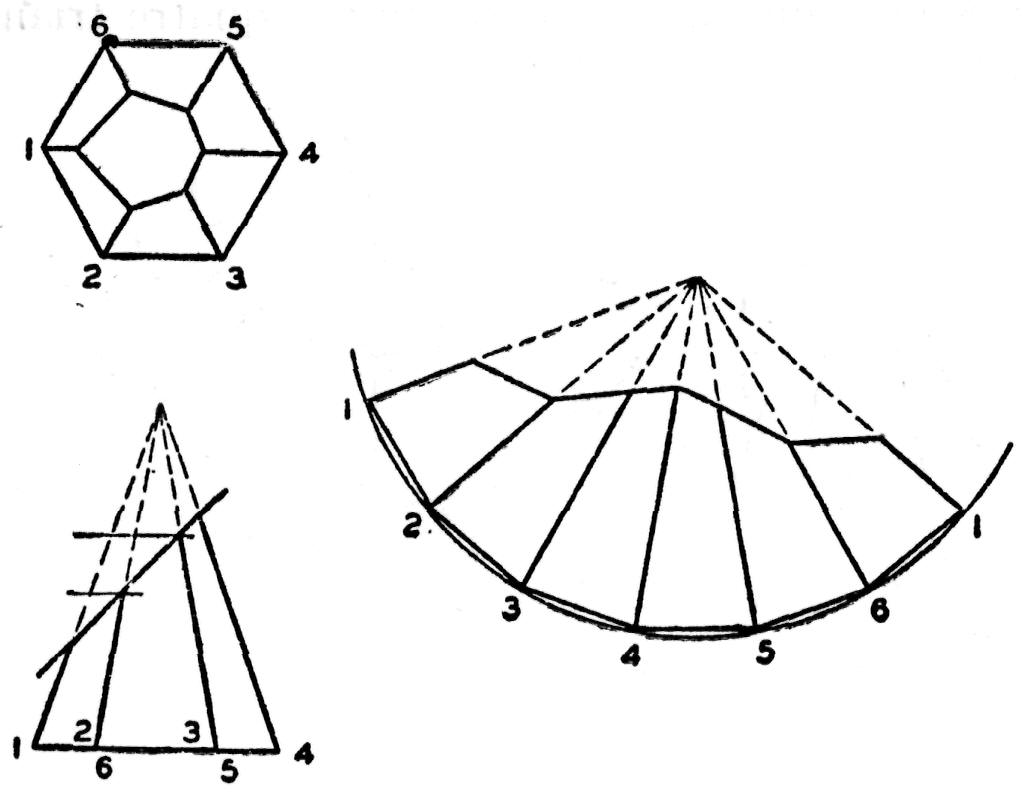
Fig. 187.— Développement d'une pyramide tronquée obliquement.
On joint ensuite par des droites les points d'intersection 1', 2', 3', 4', etc. La base supérieure, ayant pour côté N, est ensuite ajoutée au-dessus de la petite base de l'un des six trapèzes ainsi obtenus.
S'il s'agit, par ailleurs de développer une pyramide tronquée obliquement, on commence par dessiner deux vues de l'objet afin d'en déterminer la forme et les dimensions. La vue en élévation doit être construite de manière à laisser voir le sommet de la pyramide (fig. 187), mais il n'est pas nécessaire de terminer la partie supérieure du dessin dans tous ses détails; des pointillés suffisent à fournir les renseignements essentiels.
La vue de dessus donne le contour de la base et, partant, la largeur des côtés de la pyramide. Comme point de départ, on choisit un centre et, de ce centre, le patron entier de la pyramide est développé comme nous l'avons décrit ci-dessus à propos de la pyramide hexagonale.
En admettant qu'on veuille commencer le patron par l'élément le plus court, on trouvera la vraie grandeur de cet élément dans la vue d'élévation.
Quant à l'élément 2, la vue en élévation n'en montre pas la vraie grandeur du fait qu'il se trouve incliné par rapport au plan de projection; pour trouver cette grandeur, on imagine que la pyramide est tournée de manière que cette arête se place dans la position de l'élément 1 afin que sa vraie forme puisse être vue.
On arrive à cela en traçant une ligne horizontale à partir de l'extrémité supérieure de l'élément 2 jusqu'au point où elle recoupera l'élément 1. La vraie grandeur de l'élément 3 est trouvée de la même manière. L'élément 4 est montré en vraie grandeur. A ce point, on a la moitié du patron; l'autre moitié en est la réplique exacte.
Cône droit
Le développement d'un cône circulaire Droit (right cône) (fig. 188) se compose du Cercle de base et d'un secteur de cercle ayant pour rayon la hauteur inclinée du cône lui-même.
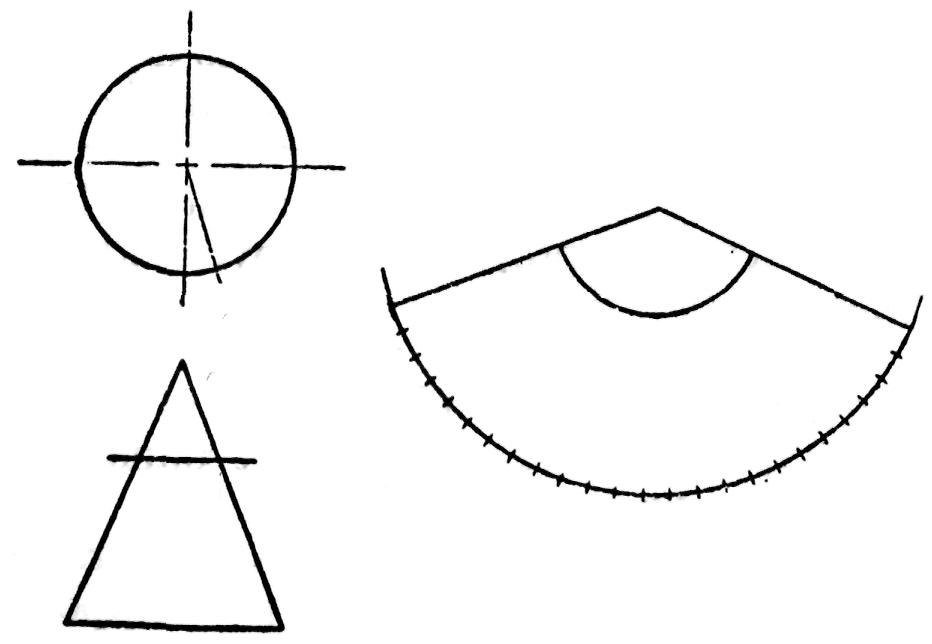
Fig. 188.— Développement d'un cône droit.
Du fait que l'un des côtés du patron (le secteur) doit toujours être équivalent en longueur à la circonférence de la base du cône, on commence par établir cette distance sur la circonférence la plus grande du patron. Pour cela, on a recours à la méthode approximative que nous avons précédemment décrite (Développement en trait parallèle). Il suffit ensuite de relier par des lignes droites les points établis de cette manière avec le centre pour achever le développement.
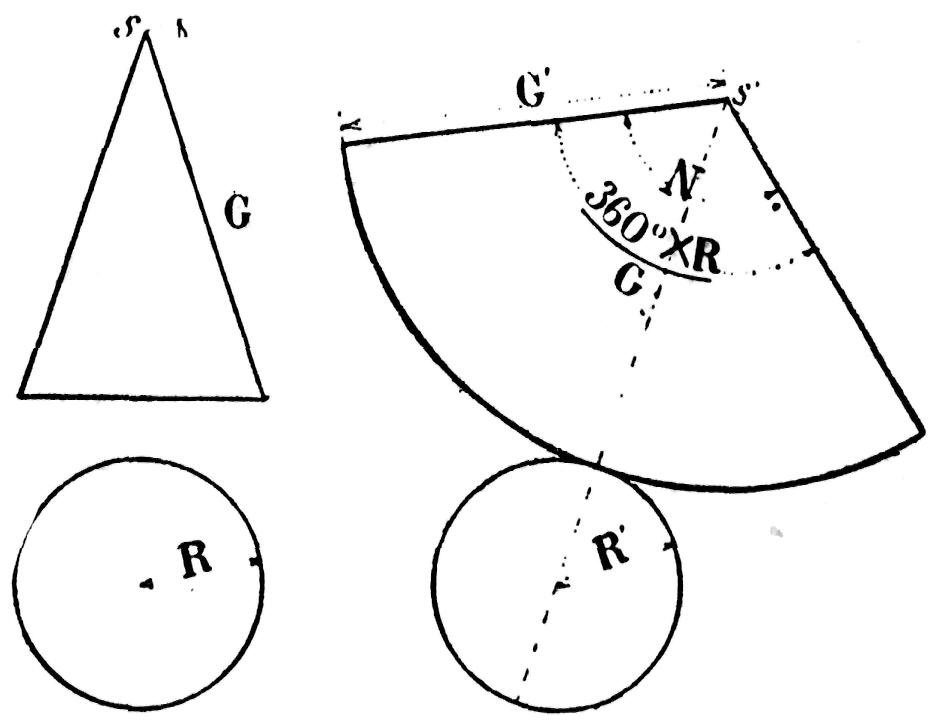
Fig. 189.—- Développement du solide d'un cône circulaire droit.
Si l'on voulait obtenir un cône tronqué, il suffirait de prendre comme rayon d'un arc — Dont le centre resterait le centre du patron — La longueur de la partie tronçonnée prise sur la pente même du cône.
Une fois le patron découpé, les deux côtés rectilignes du segment sont rapprochés pour former le cône.
Pour obtenir le développement des solides, tant pour le cône que pour le tronc de cône, il suffit d'y ajouter les bases comme le montrent les figs. 189 et 190.
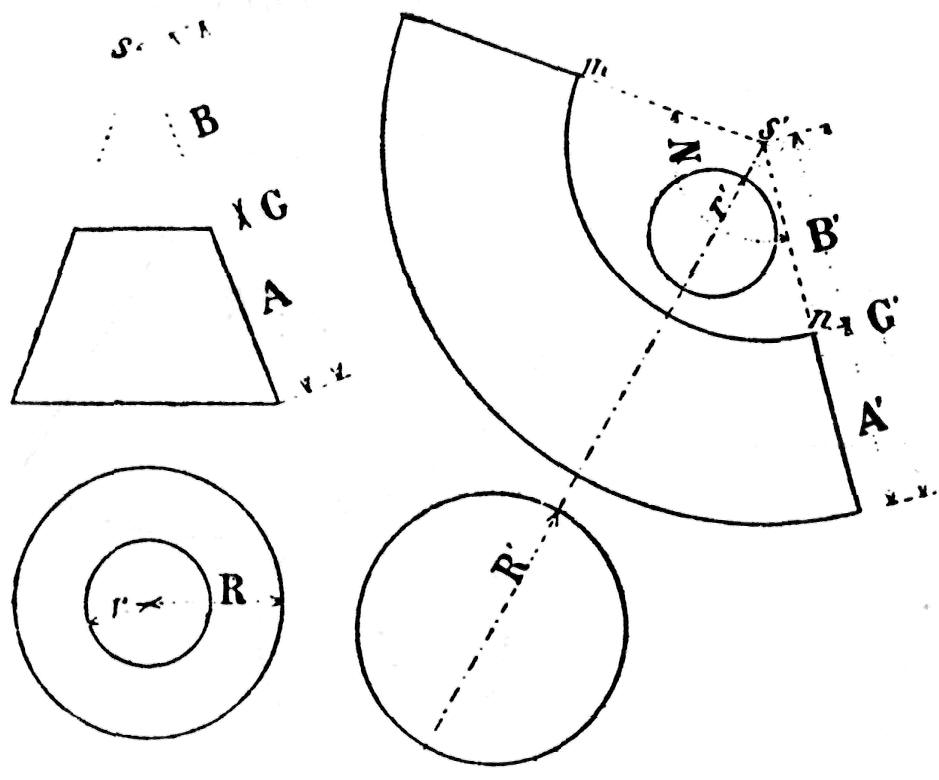
Fig. 190.— Développement du solide d'un tronc de cône circulaire droit, à
bases parallèles.
Le patron d'un cône droit tronqué obliquement (fig. 191) s'inspire des mêmes procédés d'ensemble que nous venons d'exposer. Les éléments du cône sont prolongés jusqu'à leur point de rencontre de manière à fournir l'arc du patron.
La circonférence de la base du cône est développée sur cet arc par la méthode approximative. Chacune des divisions ainsi obtenues est reliée au centre. La moitié inférieure du cercle est reportée sur la vue de dessus grâce au compas à pointes sèches en gardant le même écartement pour chacune des divisions.
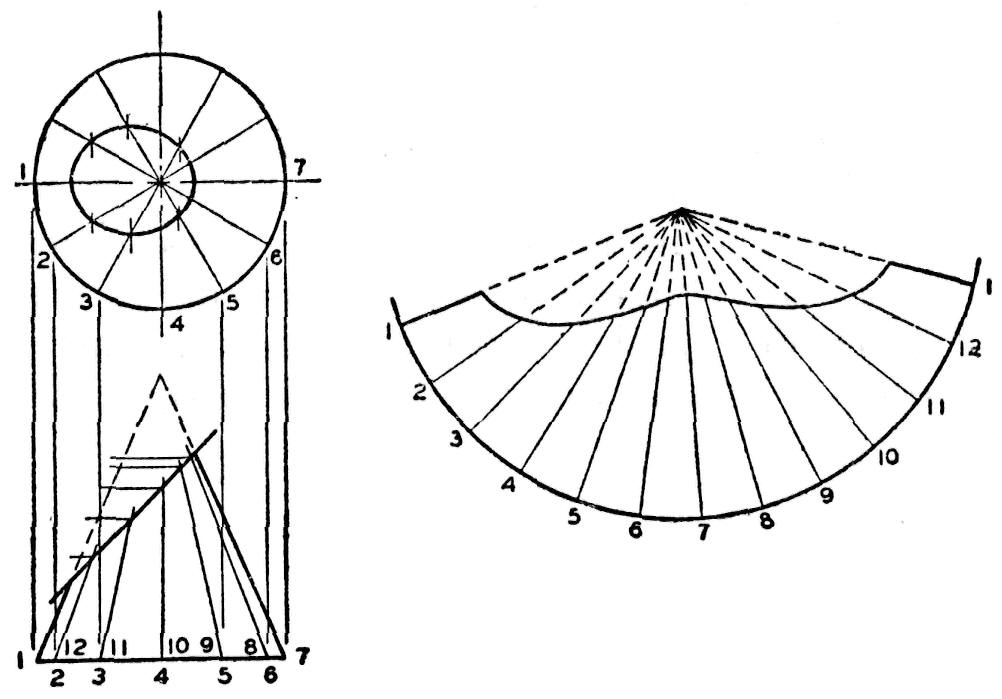
Fig. 191.— Développement d'un cône droit tronqué obliquement.
Des points ainsi repérés sur le cercle, des lignes verticales sont abaissées vers la base du cône jusqu'à ce qu'elles recoupent la ligne de celle-ci dans la vue en élévation. De ces points d'intersection, on trace des lignes se dirigeant vers le sommet du cône; ces lignes doivent s'arrêter au point où elles recoupent le trait oblique qui délimite le sommet du cône tronqué.
Ces lignes forment les éléments qui correspondent à ceux qu'on a développés sur le patron. Pour trouver la vraie grandeur de chaque ligne de la vue en élévation, on projette une horizontale à partir de chaque point de l'oblique formant sommet jusqu'au point où elle recoupe l'élément en vraie grandeur du cône. Ces lignes horizontales repéreront des longueurs correspondant aux vraies grandeurs de chaque ligne. Il est préférable de numéroter les éléments correspondants sur chacune des vues afin de faciliter le report des vraies grandeurs de la vue en élévation à la vue qui forme le développement du patron.
