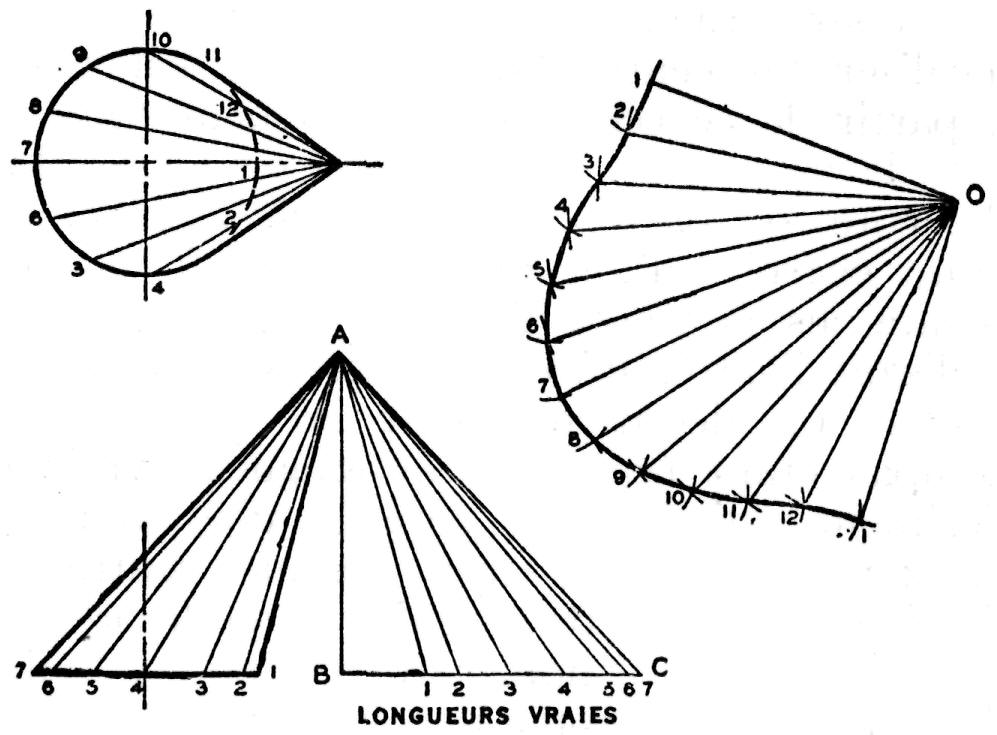
Fig. 192.— Développement par triangulation d'un cône oblique, à base circulaire.
Développement par triangulation
Dessin et développement des tôles
II arrive fréquemment, dans les problèmes qui se rattachent au développement de certaines surfaces, que les vues orthographiques de l'objet à développer ne font pas voir les vraies dimensions des surfaces qui doivent constituer le patron.
Ce cas s'est présenté à propos de la pyramide tronquée (fig. 187), dans laquelle certains éléments ne sont pas dessinés d'après leur vraie grandeur, à cause de leur position inclinée.
Comme tous les éléments d'un cône droit sont d'égale longueur, les vraies grandeurs des lignes raccourcies d'une vue sont trouvées en faisant tourner l'objet sur un axe vertical jusqu'à ce que la ligne — ou l'élément — prenne sur le dessin une position qui en montre la vraie grandeur.
On parvient à ce résultat sur le dessin en projetant une ligne horizontale à partir du sommet de l'élément et qui se dirige vers le côté du cône. Cette ligne recoupe l'élément montré en vraie grandeur à une distance égale à la vraie grandeur de l'élément raccourci.
Dans un développement effectué à l'aide de la triangulation, on imagine que l'élément incliné est l'hypoténuse d'une section triangulaire droite, dont la base est le rayon de la base du cône et l'altitude sa hauteur verticale. Le triangle est alors tourné jusqu'à ce que l'hypoténuse soit parallèle au plan de projection, montrant ainsi sa vraie grandeur.
Il s'ensuit que la triangulation est basée sur l'utilisation d'un triangle rectangle droit pour déterminer les vraies grandeurs de chaque ligne sur la surface à développer. Dans certains cas, il est nécessaire de montrer les éléments en deux vues afin de trouver le moyen d'établir leurs vraies grandeurs. Une vue en élévation fait voir la hauteur verticale d'un élément et un plan ou vue de dessus fait voir la distance horizontale couverte par ce même élément. Si, alors, ces deux distances sont développées comme les côtés d'un triangle rectangle droit, l'hypoténuse du triangle donne la vraie longueur de l'élément.
En guise d'application de la théorie un peu abstraite que nous venons d'exposer, prenons le cas d'un cône oblique à base circulaire dont la surface doit être développée (fig. 192).

Fig. 192.— Développement par triangulation d'un cône oblique, à base
circulaire.
Les vues en élévation et en plan sont dessinées, puis divisées en éléments. Dans la vue en élévation, le côté le plus court (A1) du cône est celui dont la largeur est la moindre sur le patron (O1) et le côté le plus long (A7) est celui dont la largeur est la plus grande sur le patron (O7).
Ces deux lignes correspondent aux éléments qui s'abaissent sur la ligne d'axe horizontale de la vue en plan, d'où l'on conclut Que toute ligne d'élément qui est horizontale dans la vue en plan, paraît en vraie grandeur dans la vue en élévation.
Dans la vue en élévation, la distance verticale AB du sommet du cône à la ligne de base est la hauteur verticale de tous les éléments, tandis que les longueurs de tous les éléments que fait voir la vue en plan sont développées à angle droit de cette hauteur verticale AB le long de BC. L'hypoténuse de chacun des triangles ainsi formés est la vraie longueur de l'élément auquel elle correspond.
Pour former le patron, on commence par localiser un centre O. Une ligne est tracée à partir de ce centre d'une longueur égale au côté le plus court du cône afin de former l'un des côtés du patron. Les branches du compas étant écartées d'une distance égale à celle qui sépare les éléments dans la vue en plan, et utilisant l'extrémité externe de la ligne comme centre, on décrit un petit arc.
Ensuite, le compas étant écarté de la longueur vraie de l'élément adjacent au côté le plus court, et prenant l'axe du patron comme centre, on décrit un autre petit arc qui recoupe le premier. Ce point d'intersection marque l'une des limites du contour du patron à développer.
Les pointes du compas étant ensuite réglées sur le premier rayon utilisé et en prenant comme centre l'intersection des deux arcs précédemment décrits, on décrit un nouvel arc; la vraie longueur du prochain élément est alors utilisée pour recouper ce nouvel arc comme tout à l'heure, ce qui donne un nouveau point pour le contour du patron. Le même manège est continué jusqu'à ce qu'on ait trouvé la vraie longueur de tous les éléments, puis les points où deux arcs se recoupent sont reliés au moyen d'une légère courbe, tracée au pistolet, pour donner l'approximation finale du contour du patron.
Voici une deuxième application un peu plus simple et qui contribuera à mieux faire comprendre la marche à suivre. Il s'agit, cette fois, d'un capot de moteur (engine cowling). Le développement de cette pièce en tôle s'exécute facilement à l'aide de la triangulation (fig. 193).

Fig. 193.— Développement par triangulation d'un capot de moteur en tôle.
Observez d'abord que les vues de cet objet ne sont pas présentées selon les règles conventionnelles du dessin de machines. Lorsqu'il s'agit du développement des tôles, les dessinateurs préfèrent souvent une présentation pratique à un dessin trop technique; l'essentiel est d'être parfaitement compris.
On commence par dessiner la vue de côté I et la vue de face II en vraie grandeur. Dans le présent cas, l'extrémité avant et l'extrémité arrière forment des demi-cercles — dans d'autres cas, il arrive souvent qu'on ait affaire à des courbes plus ou moins régulières.
On divise ensuite l'extrémité arrière en un nombre convenable de parties égales — disons sept — que l'on numérote de 1 à 7. L'extrémité avant est ensuite divisée du même nombre de parties qui seront identifiées par des lettres de A à G.
Reliez par des lignes droites le point 1 au point A, puis A à 2, 2 à B, et ainsi de suite pour former de petits triangles.
A un endroit approprié du dessin, tracez une ligne horizontale AX (vue III) d'une longueur égale à la longueur du bord horizontal de l'objet. A l'extrémité gauche de cette ligne, élevez une perpendiculaire de longueur indéterminée.
La première chose à faire dans la construction du développement consiste à trouver la longueur vraie du côté du triangle A1. Avec votre compas, reportez la longueur de la ligne A1 de la vue II à la ligne verticale X2 de la vue III. Sur cette ligne verticale, inscrivez le point 1.
Ensuite tracez la ligne 1A qui représente la longueur vraie de A1 sur l'objet. A l'aide du compas, reportez cette longueur ailleurs sur votre feuille de papier à dessin ou sur la tôle même pour obtenir la ligne A1 de la vue IV. (Sur notre fig. 193 cette ligne est brisée parce qu'il y aura au-dessus de la ligne A1 une autre partie du capot de moteur que ne fait pas voir le développement).
Avec votre compas, mesurez maintenant la distance de 1 à 2, sur la vue II et, vous servant du point 1, vue IV, comme centre, décrivez un arc.
Trouvez la longueur vraie de A2 de la même manière que vous avez trouvé celle de A1 et reportez cette distance sur le développement.
Vous y parviendrez en plaçant l'une des branches du compas sur A et en décrivant un arc qui recoupera le petit arc obtenu en prenant 1 comme centre. Tracez la ligne A2. Ceci complète les deux côtés du premier triangle. Ne reliez pas les points 1 et 2 tant que le développement n'aura pas été entièrement terminé.
Pour trouver le deuxième triangle, prenez la distance AB (vue II) et, vous servant de cette distance comme rayon, décrivez un arc ayant le point A de la vue IV comme centre.
Puis, de la même manière que précédemment décrit, trouvez la longueur vraie de B2.
Décrivez un arc du point 2 pour recouper le petit arc (précédemment décrit avec A comme centre), et tracez la ligne B2.
Continuez ainsi jusqu'à ce que vous ayez développé la moitié du capot de moteur. Reliez les points A à G et 1 à 7, afin de compléter la moitié gauche de votre développement.
Du fait que l'objet est symétrique, il ne sert de rien de prolonger le travail de développement.
En prenant la ligne A1 comme centre, le contour de l'autre moitié du capot peut être tracé en utilisant le revers de la moitié déjà développée.
Raccords de transition
Les raccords de transition dont la fig. 194 nous fait voir un échantillon typique, servent à relier entre elles des ouvertures dont les surfaces de section sont de formes différentes. Le développement de ces raccords s'accomplit, comme le précédent, au moyen de la triangulation.

Fig. 194.— Développement par triangulation d'un raccord de transition.
Dans le cas qui nous occupe, il s'agit d'un raccord servant à relier une canalisation carrée à un tuyau circulaire, les deux ayant le même axe.
Vous commencez par décrire un cercle et un carré (vue I) représentant une vue de dessus de l'objet.
Les dimensions du cercle et du carré sont déterminées par celle des deux conduites que l'on veut raccorder.
De manière à s'emboîter parfaitement sur les tuyaux, la transition doit avoir quatre sur- Faces triangulaires plates qui vont en diminuant vers un point du cercle, et quatre segments coniques qui vont en diminuant vers un point aux angles du carré.
Commencez par diviser la moitié du cercle (vue I) en huit arcs égaux en vous servant du compas; ensuite reliez les cinq points ainsi repérés sur chaque quart du cercle avec l'angle correspondant du carré.
Numérotez chaque point. La vue de dessus permet maintenant de voir la moitié des quatre segments coniques et la moitié des quatre surfaces triangulaires plates. Du fait que ce raccord de transition est symétrique, il suffira de n'en développer qu'une moitié.
Faites alors vos projections de manière à développer la vue de côté II.
A un endroit convenable de votre feuille de papier ou de tôle, tracez une ligne horizontale XY (vue III) d'une hauteur égale à celle du raccord. Érigez une perpendiculaire XZ de longueur indéterminée.
Normalement, pour fabriquer cette pièce de transition en tôle, on ferait le joint en A1 (vue I).
C'est l'endroit tout désigné pour servir de point de départ au développement. Pour trouver la longueur vraie de A1, reportez, à l'aide du compas, la longueur de A1 de la vue à la ligne verticale de la vue III.
Sur cette ligne verticale, marquez le point A. Ensuite, tracez la ligne AX, qui représente la longueur vraie de A1 sur le raccord de transition même.
Passons maintenant à vue IV. A un endroit convenable, tracez la ligne A1 et marquez les extrémités.
Avec le compas, mesurez la distance de A à B dans la vue I, et avec le point A de la vue IV comme centre, décrivez un arc. Trouvez la vraie longueur de Bl de la même manière que vous avez trouvé celle de A1 et reportez cette distance sur le développement en utilisant A1 comme rayon et le point B de la vue IV comme centre pour décrire un arc qui recoupera le petit arc antérieurement décrit avec A comme centre.
Marquez l'intersection B et tracez la droite AB. Ceci complète le triangle AB1.
Réglez l'écartement des branches de votre compas à la longueur de 1-2 sur le cercle de la vue I et ensuite, sur la vue IV, décrivez un arc en prenant le point 1 comme centre.
Pour trouver le deuxième triangle, servez-vous d'un rayon de la vraie longueur de la ligne B2 et décrivez un arc avec le point B de la vue IV comme centre, de manière à recouper le petit arc antérieurement décrit avec le point 1 comme centre. Ceci vous donne deux côtés du triangle 1B2.
Procédez de la même manière pour localiser les points 3, 4, et 5. La ligne B5 est d'une longueur égale à la ligne C5, et la ligne BC de la vue IV est égale à la ligne BC de la vue I.
Construisez le triangle BC5 de la vue IV.
Localisez les points 6, 7, 8 et 1 de la même manière que vous avez repéré les points 1, 2, 3, 4 et 5.
Construisez le triangle CD1, qui est semblable au triangle AB1.
Reliez les points 1, 2, 3, 4, 5, 6, 7, 8 et 1 par une courbe légère, tracée au pistolet, ce qui terminera la moitié de votre développement. Comme ce raccord est symétrique, servez-vous — comme précédemment à propos du capot de moteur — de cette première moitié en guise de gabarit pour tracer la deuxième moitié.
Votre développement est maintenant terminé.
Si les deux canalisations n'avaient pas le même axe, il serait nécessaire de construire la totalité du développement en ayant recours à la triangulation.
On peut procéder plus simplement pour développer ce même raccord de transition (fig. 194) du fait que chaque quart en est de forme absolument identique aux autres.
Construisez le triangle AB1.
Repérez les points 1, 2, 3, 4 et 5.
Construisez le triangle B5K.
Sachant que cette pièce de transition est de forme symétrique, il est clair que 1A doit égaler 5K et que AB doit égaler BK. Vous servant de la vraie longueur de 1A comme rayon, et du point 5 (vue IV) comme centre, décrivez un petit arc.
Ensuite, vous servant de la vraie longueur de AB comme rayon et du point B (vue IV) comme centre, décrivez un autre arc qui viendra recouper celui qui vient d'être tracé.
Marquez l'intersection K et tracez des droites pour compléter le triangle B5K. Vous avez un quadrant.
Projetez les lignes A1 et K5 jusqu'à ce qu'elles se recoupent au point L, de manière à établir le centre de votre développement.
Du point L comme centre, décrivez un rayon qui passe par les points 1, 2, 3, 4 et s'arrête à 5.
Si vous pliez sur la ligne LK le développement 12345KBA1, vous aurez le patron exact du développement 56781DCK5.
Développements spéciaux

Fig. 195.— Autre développement d'un raccord de transition.

Fi. 196.— Exercices de développement de raccords divers en tôle.

Fig. 197.— Raccord de transition dont une extrémité forme ellipse.

Fig. 198.— Intersection de deux cylindres circulaires dont l'un est
obliqué par rapport à l'autre.
Fig. 199.— Raccordement de deux cylindres sans intersection.

Fig. 200.— Pénétrations: a) cylindres égaux; b) prisme et sphère; c)
Prisme et cône; d) deux cylindres inégaux.

Fig. 201.— Intersection à angle droit d'un cylindre N avec le cylindre P.

Fig. 202a.— Divers exercices de développement et de construction relatifs
à des canalisations d'air. Ces travaux peuvent être exécutés avec des modèles en
papier fort en observant les dimensions suggérées.
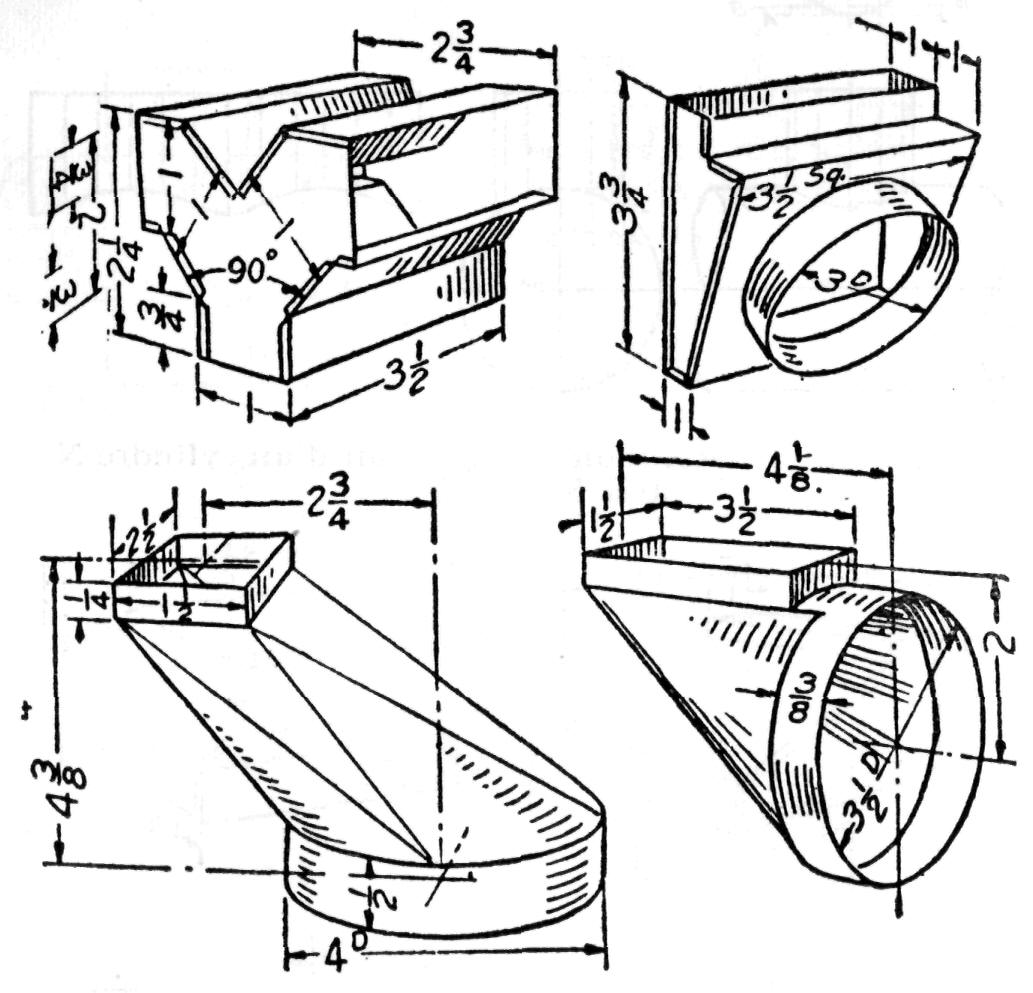
Fig. 202b.— Autres exercices de développements en tôlerie. Ces exercices
peuvent être exécutés d'abord avec du carton et doivent se conformer aux
dimensions indiquées.
