Cylindres

Cylindres tronqués

Il arrive fréquemment qu'un cylindre soit modifié par d'autres surfaces, le plus souvent par des plans. La figure 6.33 en fournit quelques exemples.

Figure 6.33
Cylindres tronqués.

En (a), la coupe exécutée sur le cylindre introduit deux surfaces planes4 qui sont facilement reconnues par les profils 15-16 et 13-16 dans la vue de droite. La distance de la ligne 3-4 au centre du cercle est égale à 13-E.

En (b), les coupes introduisent quatre surfaces planes dont les profils, dans la vue de droite, sont 23-24, 24-21, 21-22 et 22-19. La distance entre 5-6 et 7-8 est égale à 21-22 tandis que la largeur 9-10 est la même que 5-6.

En (c), une coupe horizontale pratiquée sur deux cylindres concentriques introduit une surface plane de forme en T dans la vue de dessus. Notez que la ligne 8-9 est cachée, car elle représente la partie inférieure de l'arc 22. Les largeurs 2-3 et 14-15 sont respectivement égales à 17-20 et à 18-19.

La facette 6-7-10-9 est appelée techniquement méplat ou plat.

Cylindres et ellipses

Si un cylindre est tronqué par un plan incliné, tel que celui illustré à la figure 6.34.a, la surface inclinée est limitée par une ellipse.

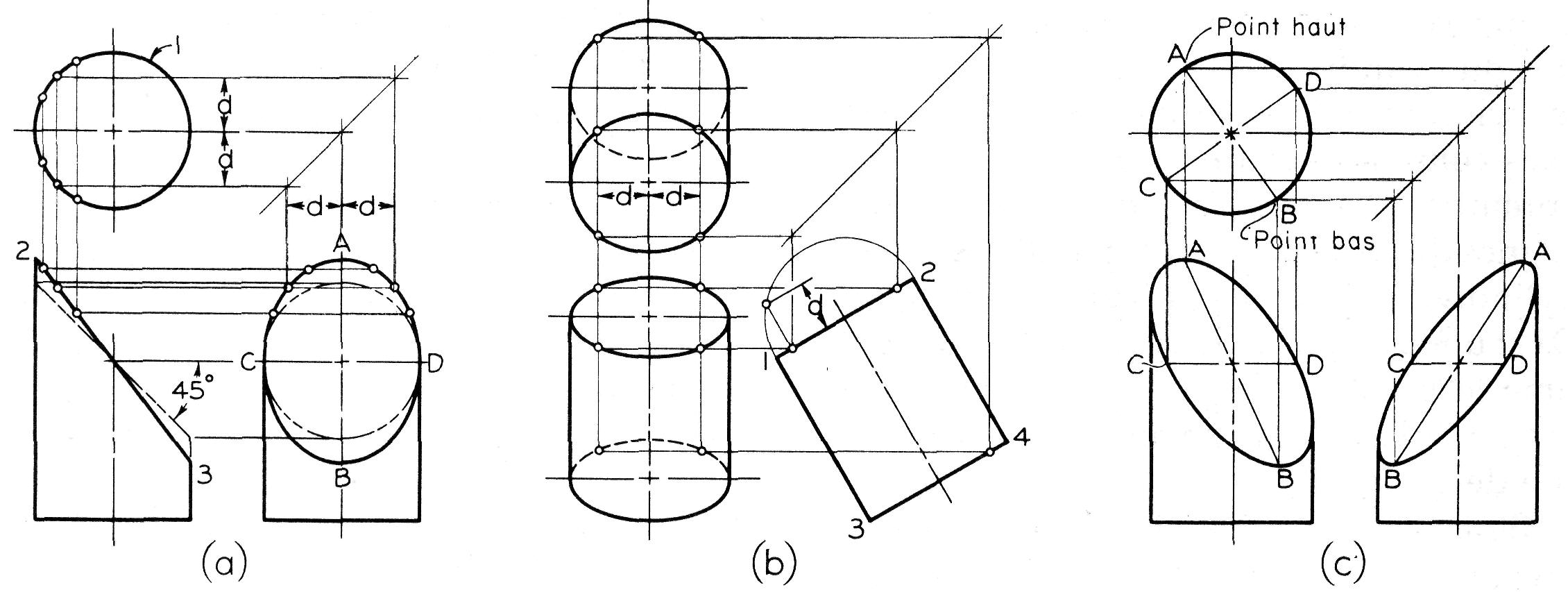
Figure 6.34
Cylindres et ellipses

Celle-ci apparaît comme le cercle 1 dans la vue de dessus, comme la droite 2-3 dans la vue de face et comme l'ellipse ADBC dans la vue de droite.

Notez que, quelle que soit l'inclinaison du plan de coupe (voir les lignes discontinues), l'ellipse est toujours vue de dessus comme le vrai cercle 1. Pour déterminer la vraie grandeur de l'ellipse, il faut utiliser une vue auxiliaire.

Les axes AB et CD de l'ellipse étant connus, on peut tracer celle-ci à l'aide d'un gabarit (figure 4.55) ou en appliquant une des méthodes illustrées aux figures 4.48 à 4.50 et 4.52.a.

Si le cylindre est penché vers l'avant (figure 6.34.b), ses bases 1-2 et 3-4 seront vues comme des ellipses dans les vues de dessus et de face.

Les points des ellipses peuvent être déterminés à partir de la vue en bout d'une extrémité du cylindre (illustrée comme un demi-cercle sur le dessin), les distances d de la vue de droite sont reportées à la vue de dessus. Les méthodes citées ci-dessus peuvent aussi être utilisées.

Si le cylindre est coupé par un plan oblique (figure 6.34.c), la face elliptique apparaîtra comme des ellipses dans deux des vues.

Dans la vue de dessus, les points A et B sont connus et représentent respectivement le point haut et le point bas de l'ellipse dans l'espace. Tracez CD perpendiculaire au diamètre AB. AB et CD sont respectivement les projections du grand axe et du petit axe de l'ellipse réelle dans l'espace.

Dans la vue de face, les élévations de A et de B sont connues au préalable, CD est nécessairement horizontal, car il est projeté en vraie grandeur, comme le petit axe de l'ellipse réelle, dans la vue de dessus.

Les axes AB et CD dans les vues de face et de droite sont les axes conjugués des ellipses et ils ne sont pas des axes de symétrie. Pour tracer les ellipses, utilisez les méthodes déjà citées.

La figure 6.35 illustre l'intersection d'un plan incliné et d'une moulure quart-de-rond I (a) ainsi que celle d'un plan incliné et d'un cavet (b).

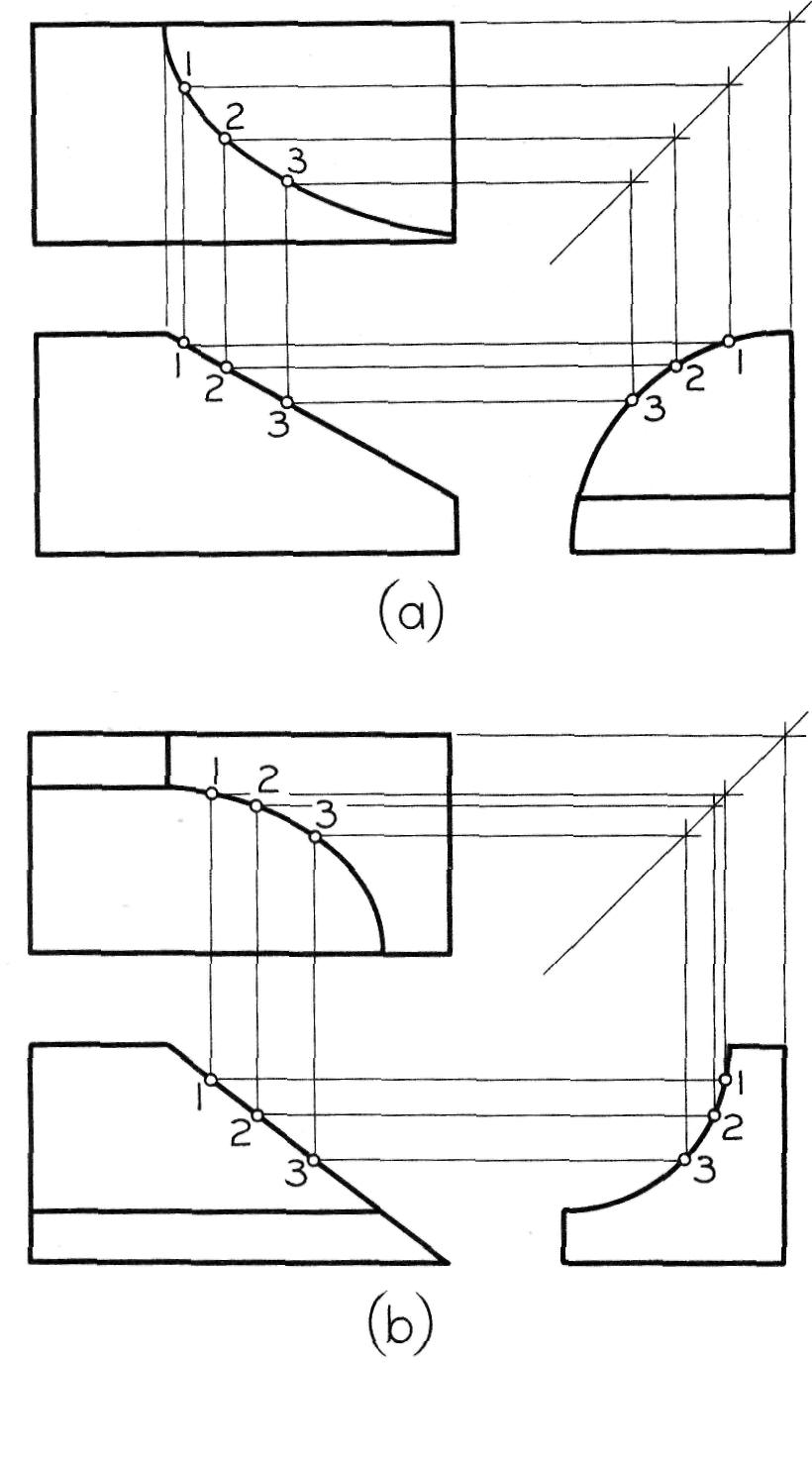
Figure 6.35
Tracé d'une courbe elliptique.

Dans chaque cas, il suffit de déterminer les points, choisis au hasard sur les vues de face et de droite, et de les relier ensuite à l'aide d'un pistolet.