Comment les circuits comprennent les uns et les zéros
Mes premiers pas en Électronique
Les téléphones portables, les ordinateurs, les téléviseurs, les consoles de jeux vidéo et presque toutes les autres technologies que vous voyez autour de vous sont composés d'électronique numérique.
Si vous avez déjà observé l'intérieur d'un ordinateur, les circuits peuvent paraître complexes, mais une fois décomposés, c'est en réalité assez simple : chaque action d'un ordinateur dépend de la présence d'une tension élevée ou basse sur un circuit.
Vous avez utilisé des transistors pour créer des circuits de contrôle, et dans cette section, vous apprendrez les bases de l'électronique numérique pour créer des circuits encore plus intelligents.
Vous allez découvrir un nouveau
système numérique, ce que sont les bits et les octets, et comment les utiliser
pour créer des messages électriques.
Uns et zéros comme tensions
À l'école, mon professeur m'a expliqué que les ordinateurs utilisaient
des uns et des zéros pour communiquer, mais il ne m'a pas donné plus
d'explications. Je voulais en savoir plus, alors j'ai décidé de demander à mon
père.
Les ordinateurs étant des machines complexes, je pensais que leur
utilisation des uns et des zéros serait également complexe, mais mon père m'a
dit :
« Dans un ordinateur, un est juste un fil sous tension, et un zéro est un fil sans tension. »
(Par « sans tension », mon père voulait dire que la tension était nulle.)
Dans « Comment régler la vitesse de sortie du temporisateur 555 » à la section Construire un instrument de musique, j'ai brièvement mentionné que les broches du temporisateur 555 pouvaient être hautes ou basses.
Les broches des circuits intégrés d'un ordinateur fonctionnent de la même manière : hautes pour un, basses pour zéro. Les circuits numériques fonctionnent en inversant les tensions sur différents fils entre haute et basse.
Découvrez le système de numération binaire (voir aussi Le code Binaire et Le code Binaire Suite...)
Normalement, lorsqu'on parle de nombres, on utilise des nombres décimaux, qui sont en base 10.
En base 10, un chiffre peut avoir une des 10 valeurs possibles, de 0 à 9.
Mais les circuits numériques ne peuvent fonctionner qu'avec deux tensions (haute et basse), et ne peuvent donc comprendre que les nombres binaires.
Le système binaire est également appelé système de numération en base 2, et les chiffres d'un nombre binaire n'ont que deux valeurs possibles : 0 et 1.
Voici comment compter jusqu’à 10 en décimal et en binaire :
| Nombre décimal | Nombre binaire |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
Que se passe-t-il ici ?
Le nombre 2 en décimal est égal
à 0010 en binaire, et le nombre 4 en décimal est égal à 0100 en binaire !
On peut déterminer la valeur de n’importe quel nombre dans n’importe quel
système en utilisant les chiffres et leur position. Le chiffre le plus à droite
est toujours multiplié par 1.
En allant vers la gauche, la
valeur de chaque position est égale à la base multipliée par la valeur de la
position précédente.
En décimal, la base est 10, donc la valeur de la
deuxième position est 10, soit 10 × 1 ; la valeur de la troisième position est
100, soit 10 × 10 ; la valeur de la quatrième position est 1 000, soit 10 ×
100 ; et ainsi de suite.
Voici un exemple :

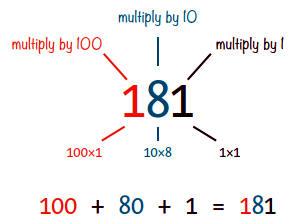
Dans le nombre 181, le premier chiffre est 1, le deuxième 8 et le troisième 1.
Une fois ces chiffres multipliés par leurs valeurs de position, vous pouvez additionner les valeurs obtenues pour obtenir 181.
Cette méthode n'est cependant
pas nécessaire pour calculer les nombres décimaux. Il est clair que 181 est égal
à 181 !
Cette méthode est très utile pour trouver la valeur des nombres
binaires. Le binaire suit les mêmes règles, mais utilise une base de 2.
Projet n° 18 : Conversion de binaire en décimal
Dans ce projet,
vous allez convertir un nombre binaire en décimal. Convertir un nombre dans une
autre base consiste simplement à calculer sa valeur et à l'écrire avec les
chiffres de cette nouvelle base.
Outils
Un stylo ou un crayon pour
écrire.
Du papier pour écrire.
Une calculatrice pour additionner des nombres. Si vous êtes doué pour les calculs de tête, essayez ce projet sans calculatrice.
Étape 1 : Écrivez-le sur papier
Tout d'abord, écrivez un nombre binaire à huit chiffres sur papier, en laissant un espace entre les chiffres, au-dessus et en dessous.
Je vais convertir le nombre binaire 1011 0101, et je l'écris ainsi :

Étape 2 : Écrire les valeurs des positions
Ensuite, inscrivez la valeur de chaque position au-dessus de chaque chiffre. Le binaire fonctionne de la même manière que le décimal, mais la base est 2.
Cela signifie que la valeur de la position la plus à droite est 1,
et pour trouver la position suivante à gauche, il faut multiplier la valeur de la position précédente par 2.
Par exemple, la valeur de la deuxième position est 2 × 1 = 2 ;
la valeur de la troisième position est 2 × 2 = 4 ;
la valeur de la quatrième position est 4 × 2 = 8 ; et ainsi de suite.
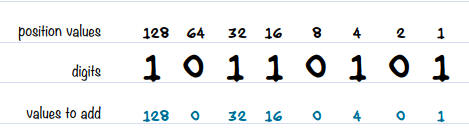
Utilisez une calculatrice si vous ne voulez pas tout calculer de tête. En écrivant ces valeurs, vous devriez obtenir quelque chose comme ceci :

Étape 3 : Calculer la valeur de chaque chiffre
Regardez chaque chiffre du nombre binaire que vous avez noté.
Si un chiffre est 0, inscrivez 0 en dessous.
Si le chiffre est 1, inscrivez la valeur de cette position en dessous. Ce sont ces valeurs que vous additionnerez pour obtenir votre nombre décimal final.
Étape 4 : Additionner les nombres
Vous devriez maintenant avoir trois lignes de nombres.
Additionnez les nombres de la ligne du bas (il peut être utile d'écrire un signe + entre chaque paire de nombres) pour obtenir la somme, qui correspond à la valeur décimale de votre nombre binaire.
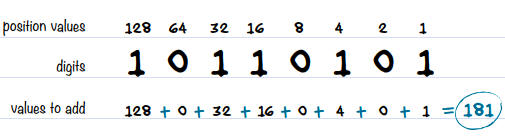
Le nombre binaire 1011 0101 est 181 en décimal.
Si vous avez suivi la méthode
avec ce nombre et que votre réponse est différente, reprenez les étapes et
comparez vos résultats aux miens pour trouver l'erreur.
Essayez :
Transformer d'autres nombres binaires
Pour vous entraîner avec les uns et les zéros, intégrons d'autres nombres binaires au monde décimal.
En voici quelques exemples :*
1010
0011 1111
1000 0000
0011 1011 0101
* En décimal, ces nombres binaires sont 10, 63, 128 et 949.
Bits et octets
Chaque chiffre d'un nombre binaire est appelé un bit (abréviation de « bit-digit » binary digit), et les ordinateurs traitent les nombres par blocs de huit bits appelés octets.
Le nombre binaire 1011 0101 possède huit bits, c'est donc un octet.
Vous pouvez interagir avec un
ordinateur de nombreuses manières, mais tous vos clics de souris, vos frappes de
touches, vos vidéos webcam, etc., doivent être convertis en bits et en octets
pour que l'ordinateur puisse les comprendre.
En fait, lorsque vous
travaillez avec des ordinateurs et autres appareils numériques, vous voyez
généralement des nombres bien plus grands qu'un seul octet.
Tous les fichiers d'un ordinateur sont des ensembles d'octets, mais si vous essayiez de décrire leur taille uniquement en octets, ces nombres seraient énormes !
C'est pourquoi les fichiers sont généralement décrits en unités plus grandes, comme les kilo-octets* (Ko), les mégaoctets (Mo), les gigaoctets (Go), les téraoctets (To), etc.
Voici la signification de ces unités :
1 kilo-octet équivaut à 1 024 octets (binaire). 1 Ko = 210 octets en base 2.
1 Ko = 1 024 octets
1 Mo =
1 024 Ko = 1 048 576 octets
1 Go = 1 024 Mo =
1 048 576 Ko =
1 073 741 824 octets
1 To = 1 024 Go =
1 048 576 Mo =
1 073 741 824 Ko = 1 099 511 627 776 octets
Si le disque dur d’un ordinateur peut contenir 1 To de données, il peut alors contenir mille milliards d’octets, soit huit mille milliards de uns et de zéros !
Les nombres peuvent être tout et n’importe quoi
Vous vous demandez peut-être : « Pourquoi aurais-je besoin de huit mille milliards de uns et de zéros dans mon ordinateur ? »
En réalité, que vous utilisiez un ordinateur pour écrire des histoires, dessiner, discuter avec vos amis, jouer à des jeux vidéo ou autre, vous utilisez ces uns et ces zéros.
Par exemple, comment un ordinateur affiche-t-il une image sur un écran ?
Un écran d'ordinateur est composé d'une multitude de petits points appelés pixels, et chaque pixel peut être réglé sur une couleur qui est un mélange de rouge, de vert et de bleu.
Pour obtenir un pixel d'un jaune éclatant, vous utiliserez des nombres pour indiquer à l'ordinateur de régler l'intensité des rouges et des verts de ce pixel à son maximum et de régler son bleu à zéro (car un mélange de rouge et de vert donne une couleur jaune).
De cette façon, vous pouvez traduire les nombres en une image à l'écran.
Projet n° 19 : Jeu de devinettes de couleurs
Dans ce projet, vous allez créer un jeu de devinettes de couleurs de pixels utilisant des valeurs binaires. Il s'agit d'un jeu à deux joueurs où vous et un ami incarnez tour à tour « l'ordinateur » et « l'utilisateur ».
L'ordinateur définit la couleur du pixel en sélectionnant une combinaison de trois boutons. Lorsque l'ordinateur est prêt, l'utilisateur doit essayer de deviner la couleur du pixel.
Lorsque l'utilisateur est prêt à deviner, il doit prononcer la couleur choisie à voix haute, puis appuyer sur le bouton révélateur de couleur pour afficher la couleur réelle.
Si l'utilisateur devine correctement, il marque un point et peut recommencer. En cas d'erreur, les rôles sont inversés. Le premier à atteindre trois points remporte la manche.
Découvrez la LED RGB
Pour créer le pixel de ce projet, vous utiliserez une LED rouge-vert-bleu (RGB), qui combine une LED rouge, une LED verte et une LED bleue en un seul composant.
En allumant et en éteignant chacune de ces LED, vous pouvez créer différentes couleurs. Par exemple, en allumant uniquement les LED rouge et verte, vous obtiendrez du jaune.
Il existe deux types de LED RGB : à anode commune et à cathode commune.
Voici à quoi ressemble une LED RGB à anode commune, ainsi que son symbole :
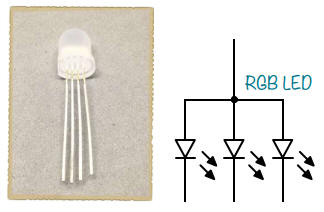
Les LED RGB ont quatre pattes.
Trois d'entre elles servent à régler la couleur, et la quatrième patte est la patte commune.
Dans les LED RGB à anode commune, les pôles positifs (anode) des trois LED sont combinés en une seule broche ; les LED RGB à cathode commune combinent les pôles négatifs (cathode) en une seule broche.
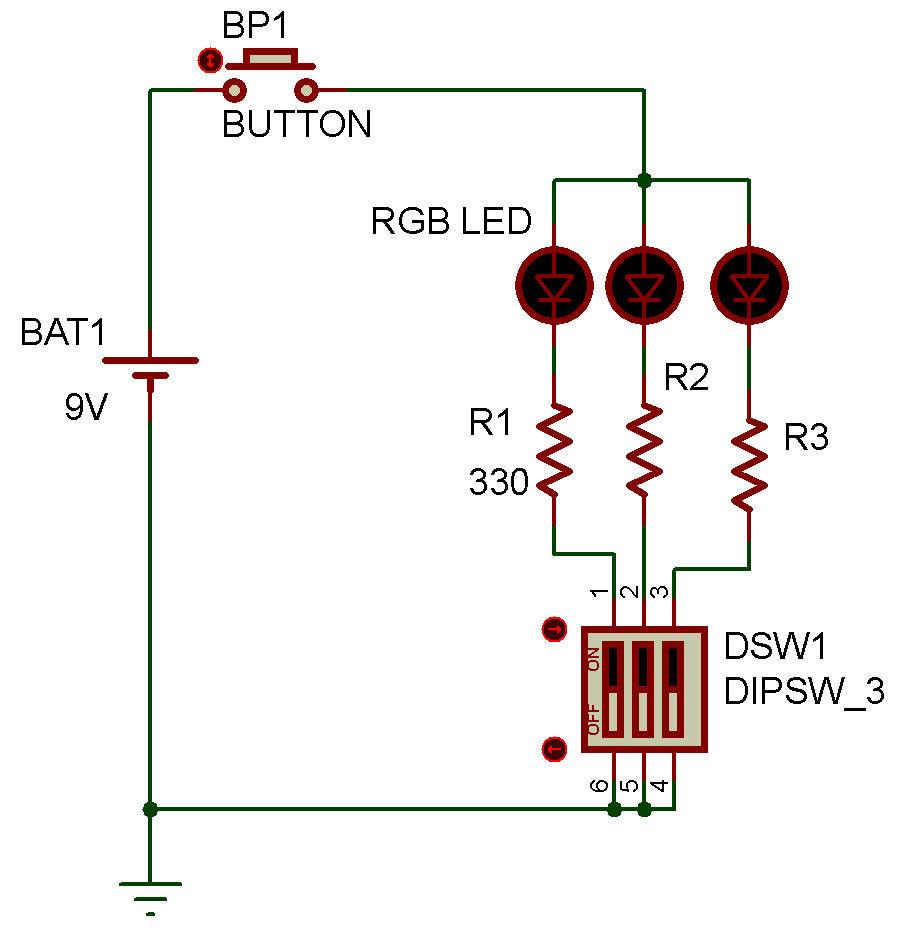
Dans ce projet, vous allez construire le circuit suivant, qui utilise une LED RGB à anode commune et des boutons.
Découvrez l'interrupteur DIP (commutateur DIP, DIP switch)
Ce circuit utilise 3 interrupteurs pour définir la valeur binaire, mais il serait fastidieux de connecter autant de boutons individuels sur votre platine d'expérimentation.
Heureusement, vous pouvez simplement utiliser un interrupteur DIP, un composant composé d'une rangée d'un ou plusieurs mini-interrupteurs.
| 3 positions | 8 positions |
 |
 |
Remarque : DIP signifie « double boîtier en ligne », ce qui correspond à la disposition des broches.
Un composant dont le nom contient « DIP » possède deux rangées de broches que vous pouvez brancher sur une plaque d'essai.
Le commutateur DIP de ce projet possède 3 commutateurs individuels.
Liste de courses Voir Fournitures utiles
Une pile standard de 9 V pour alimenter le circuit.
Une clip ou un support pour pile de 9 V pour connecter la pile au circuit.
Une platine d'essai (Breadboard) d'au moins 30 rangées.
Des fils de liaison pour faciliter la connexion des composants. (Un fil de raccordement standard convient également.)
Trois résistances de 330 Ω pour limiter le courant de la LED.
LED RGB à anode commune pour créer des couleurs.
Un bouton poussoir pour afficher les couleurs.
Un interrupteur DIP à 3 positions pour régler les couleurs.
Étape 1 : Placer les interrupteurs du sélecteur de couleurs
Orientez votre platine d'expérimentation de manière à ce que l'encoche centrale soit orientée verticalement.
Placez ensuite l'interrupteur DIP à droite en bas ;
Cela devrait vous laisser suffisamment d'espace pour connecter les composants de chaque côté des boutons, et vous pourrez ainsi séparer plus facilement les boutons de l'ordinateur de celui de l'utilisateur.
Une fois votre interrupteur en place, connectez trois fils de liaison entre la broche inférieure droite et la borne négative de l'alimentation.

Étape 2 : Connexion de la LED RGB
Au milieu de la carte, connectez votre LED RGB.
La branche la plus longue de la LED RGB est l'anode commune.
Laissez-la libre pour le moment.
Connectez une résistance de 330 Ω à chaque broche de l'interrupteur.
Connectez un cavalier à chaque branche de LED.
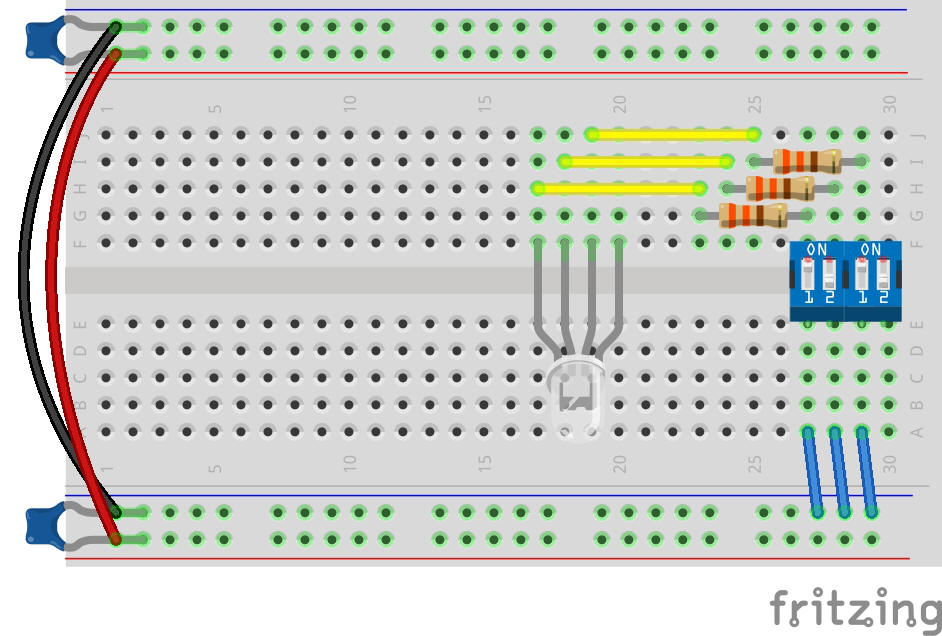
Étape 3 : Connexion du bouton révélateur de couleur
Ensuite, ajoutez le bouton qui révèle la couleur choisie par l'ordinateur à l'utilisateur.
Placez un bouton-poussoir tout en haut de la plaque d'essai, au niveau de l'encoche centrale.
Connectez un cavalier reliant la borne commune de l'anode de la LED RVB à la broche supérieure droite du quatrième bouton-poussoir.
Ensuite, connectez un cavalier reliant la broche inférieure gauche de ce bouton-poussoir à la colonne d'alimentation positive à droite.
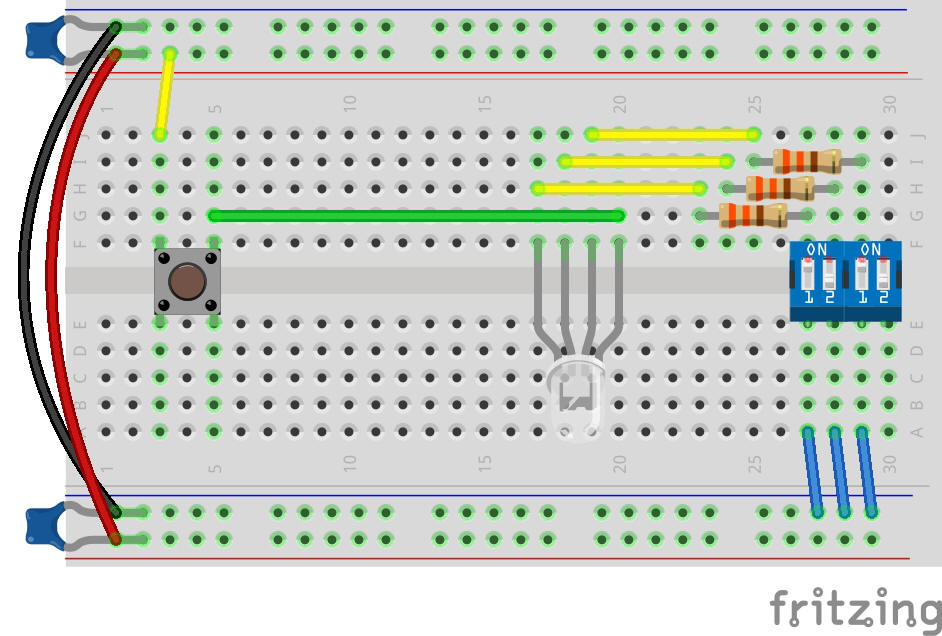
Étape 4 : Testez les couleurs
Connectez la batterie aux bornes d'alimentation et testez !
Mettez à on quelque sélecteur de l'interrupteur DIP à ON, puis sur le bouton de révélation de couleur pour voir la couleur.
Vous devriez voir les sept couleurs suivantes, selon les boutons enfoncés :
Couleur :sélecteur 1, sélecteur 2, sélecteur 3
Rouge : ON (1), OFF (0), OFF (0),
Vert : OFF (0), ON (1), OFF (0),
Bleu : OFF (0), OFF (0), ON (1),
Jaune : ON (1), ON(1), OFF (0),
Cyan : OFF (0), ON (1), ON (1),
Magenta : ON (1), OFF (0), ON (1),
Blanc : ON (1), ON (1), ON (1),
Si vos boutons ne correspondent pas à ces couleurs, inversez les fils reliant les trois résistances aux broches afin qu'ils correspondent.
Étape 5 : Que faire si le jeu ne fonctionne pas ?
Si vous ne voyez aucune couleur, vérifiez que vos connexions correspondent au schéma du circuit.
Si les connexions sont correctes et que vous ne voyez toujours aucune couleur lorsque vous appuyez sur le bouton de révélation de couleur, il se peut que vous ayez une LED à cathode commune au lieu d'une anode commune.
Pour vérifier cela, il suffit d'inverser les bornes positive et négative de la batterie.
Une fois que vous avez vérifié
que toutes les couleurs fonctionnent, invitez un ami à jouer !
Essayez :
Soudez le jeu de devinettes de couleurs
Ce circuit est idéal pour vous entraîner à la soudure. Procurez-vous une carte de prototypage et soudez le circuit dessus pour avoir un jeu de devinettes de couleurs permanent à emporter avec vous lors de vos longs trajets en voiture.
Comment les nombres binaires peuvent créer des mots
Les images ne sont pas les seules choses pouvant être stockées sous forme de nombres binaires ; on peut aussi représenter des lettres sous forme de nombres.
Une façon de procéder consiste à utiliser le code ASCII, un ensemble standard d'octets que les ordinateurs interprètent comme des majuscules et des minuscules, des chiffres, des signes de ponctuation, etc.
Les nombres de ce tableau représentent les minuscules de l'alphabet anglais.
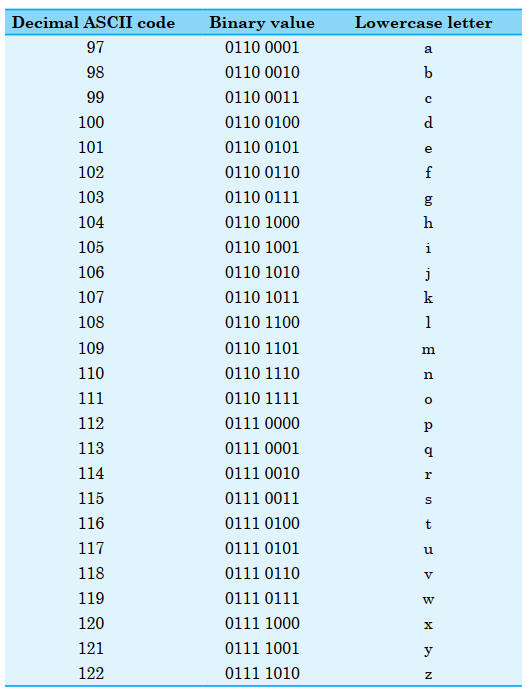
Par exemple, la lettre a peut être représentée par le nombre décimal 97, qui est le nombre binaire 0110 0001.
Vous pouvez utiliser ce tableau pour coder et décoder des messages secrets écrits uniquement avec des uns et des zéros.
Projet n° 20 : La machine à messages secrets
Ce projet est un circuit affichant des nombres binaires de huit bits grâce à des LED.
Une LED allumée correspond à 1, et une LED éteinte à 0. Vous utiliserez des interrupteurs pour définir le nombre binaire et un bouton-poussoir pour afficher le nombre binaire sur les LED.
Huit bits suffisent pour représenter un caractère ASCII ; vous pouvez donc utiliser ce projet pour générer des messages secrets déchiffrables uniquement par une personne connaissant le binaire !
Cette machine à messages secrets terminée affiche la lettre w, soit 0111 0111.
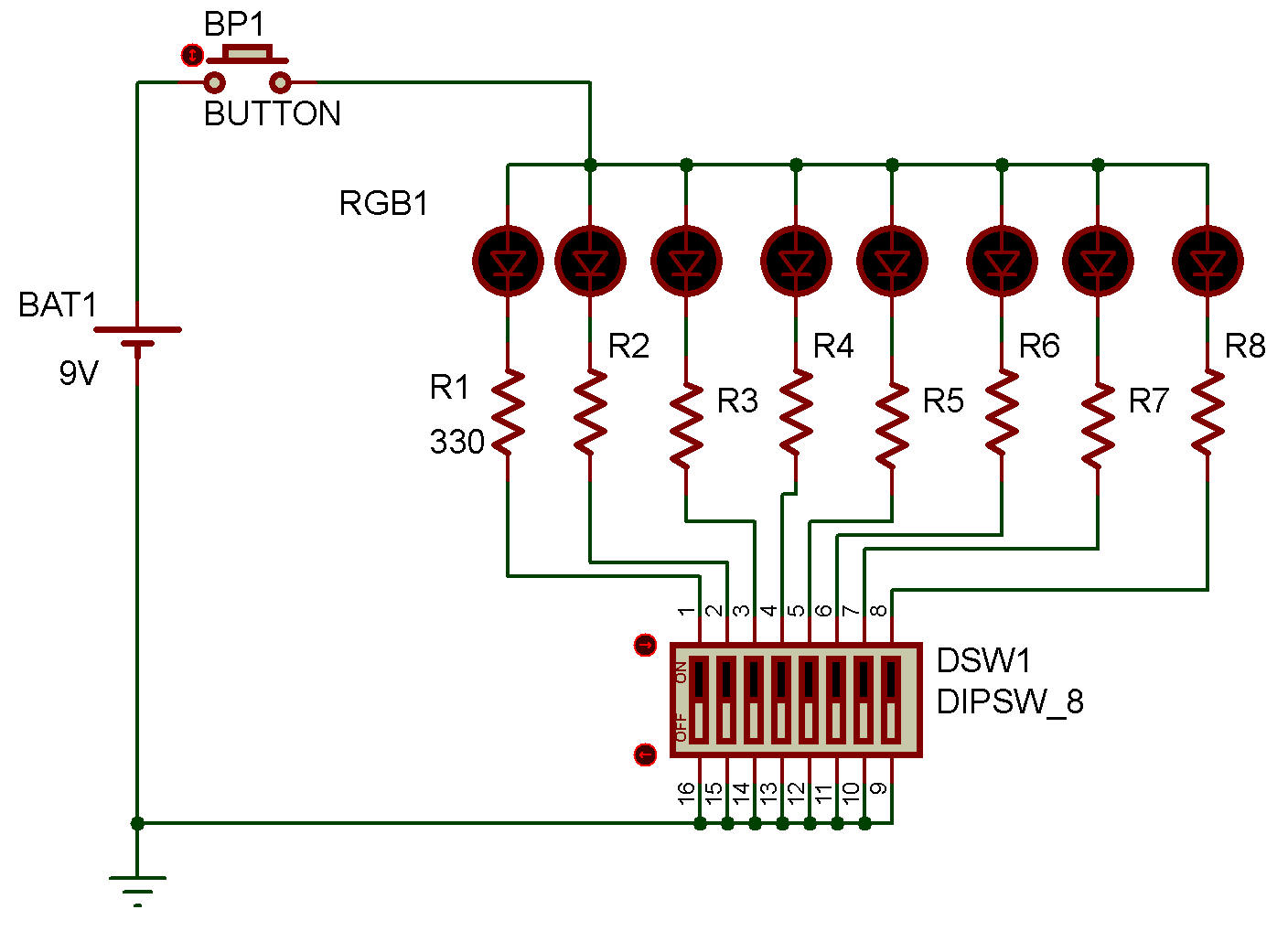
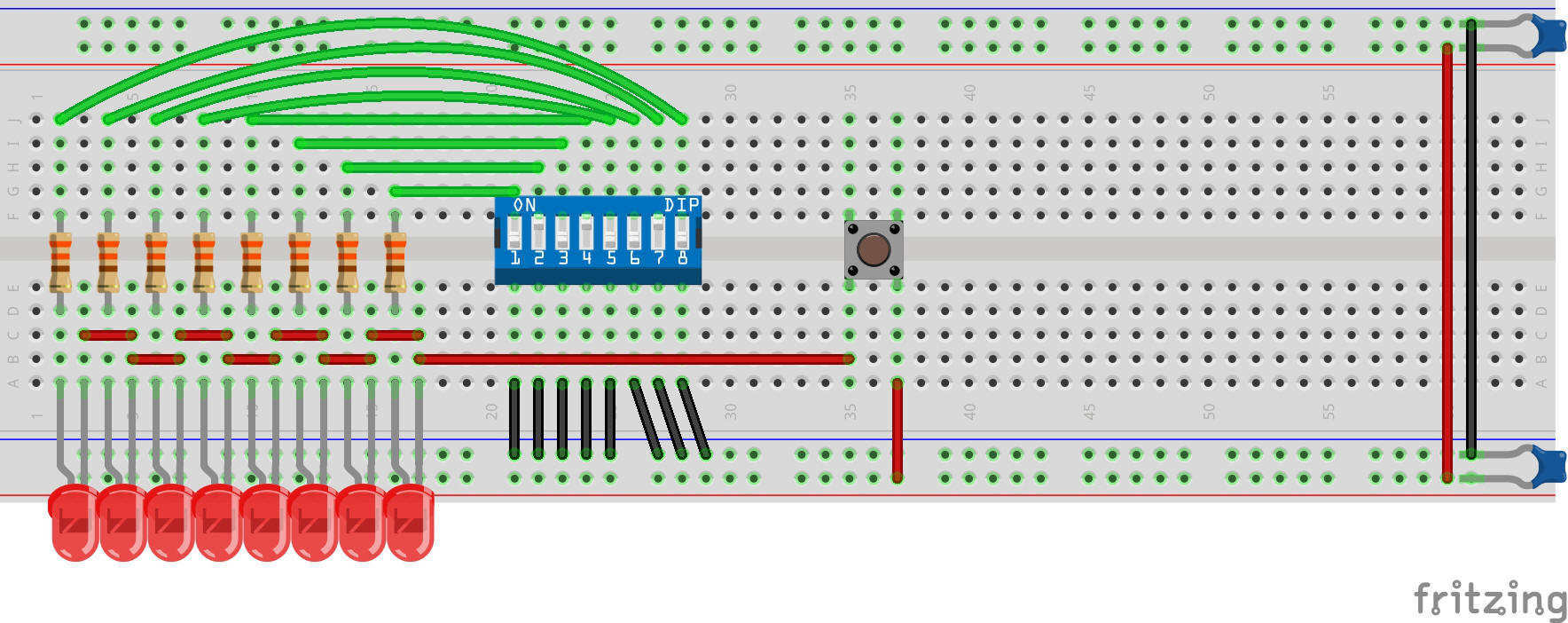
Liste de courses Voir Fournitures utiles
Une pile standard de 9 V pour alimenter le circuit.
Une clip ou un support pour pile de 9 V pour connecter la pile au circuit.
Une platine d'essai (Breadboard) d'au moins 60 rangées (Full).
Des fils de liaison pour faciliter la connexion des composants. (Un fil de raccordement standard convient également.)
Huit résistances de 330 Ω pour limiter le courant de la LED.
Huit LED pour afficher le nombre binaire.
Un bouton poussoir pour afficher le code.
Un interrupteur DIP à 8 positions pour régler les couleurs.
Étape 1 : Envoyez un message secret !
Connectez le pôle négatif de la batterie au rail négative du breadbord, puis le pôle positif au rail positif du breadbord.
Ensuite, allumez tous les interrupteurs, maintenez le bouton enfoncé pour voir si toutes les lumières s'allument, puis éteignez chaque LED une par une.
Si toutes les LED fonctionnent, il est temps de jouer !
Invitez un ami et utilisez ce circuit pour lui parler sans parler.
Asseyez-vous de chaque côté d'une table, écrivez un mot sur une feuille de papier pour votre référence personnelle et cachez-le à votre ami.
Consultez le tableau des codes ASCII et réglez les interrupteurs sur les valeurs binaires de la première lettre de votre mot.
Par exemple, l'interrupteur de la photo suivante est réglé pour afficher un a minuscule.
OFF (0) ON (1) ON (1) OFF (0) OFF (0) OFF (0) OFF (0) ON (1)
Lorsque votre bloc de commutation est prêt à afficher une lettre, appuyez sur le bouton pour allumer les LED. Maintenez le bouton enfoncé pendant que votre ami écrit la valeur binaire.
Relâchez ensuite le bouton et définissez la valeur binaire du caractère suivant.
Répétez l'opération jusqu'à ce que vous ayez affiché tous les caractères de votre mot.
Lorsque vous avez terminé, montrez le tableau des codes ASCII à votre ami pour qu'il puisse essayer de déchiffrer votre mot.
Étape 5 : Que faire si la machine à messages secrets ne fonctionne pas ?
Vous avez déjà connecté de nombreux circuits de LED, mais celui-ci comporte de nombreux composants.
Il est facile de se tromper de
connexion. Si votre circuit ne fonctionne pas immédiatement, vérifiez
soigneusement chaque connexion par rapport au schéma de ce projet.
Si
aucune lumière ne fonctionne, vérifiez d’abord que les bornes positive et
négative de la batterie sont correctement connectées.
Ensuite, vérifiez que les LED sont orientées dans le bon sens et que les résistances ont les bonnes valeurs.
Si certaines lumières fonctionnent et d’autres non, il est possible que certaines pattes des LED ou des résistances se touchent.
Inspectez-les attentivement
pour trouver l’erreur.
Pourquoi les ordinateurs utilisent des uns et
des zéros ?
Les ordinateurs utilisent des uns et des zéros au lieu
des nombres décimaux de 0 à 9, car avec seulement deux valeurs, la construction
de circuits électroniques est beaucoup plus facile, ce qui facilite les calculs
et le stockage des valeurs.
Par exemple, comme chaque chiffre n'a que deux valeurs possibles, un ou zéro, il est facile de créer un bloc mémoire simple pour stocker des nombres binaires à l'aide de commutateurs, comme vous l'avez fait avec le commutateur DIP du projet n° 20.
Il est possible de sauvegarder les uns et les zéros de différentes manières, créant ainsi de la mémoire.
Aux débuts de l'informatique, il était courant de sauvegarder des ensembles de uns et de zéros sur des cartes physiques perforées.
Aujourd'hui, de nombreux disques durs stockent les uns et les zéros sur des disques magnétiques, voire via des électrons stockés dans un circuit intégré.
Et ensuite ?
Dans cette section, vous avez appris le fonctionnement des nombres binaires.
Vous avez vu comment les uns et les zéros peuvent être utilisés pour afficher des images sur votre écran d'ordinateur et comment décoder des uns et des zéros apparemment aléatoires en texte lisible.
Pour explorer les nombres binaires plus en détail, inventez vos propres codes binaires pour les lettres de l'alphabet. Il y a 26 lettres de a à z.
Combien de chiffres faut-il pour représenter ces 26 lettres ?
Pour le savoir, vous pouvez commencer par dire que le nombre binaire 1 signifie a. Le nombre binaire suivant, 10, est b. Le suivant, 11, est c.
Notez ce nombre et continuez à augmenter jusqu'à atteindre z. Ensuite, comptez le nombre de chiffres nécessaires pour le z.
C'est le nombre minimum de chiffres dont vous avez besoin.
Voici une autre chose à essayer.
Normalement, si vous comptez avec vos doigts, vous pouvez compter jusqu'à 10, n'est-ce pas ?
Sans les pouces, on ne peut compter que jusqu'à 8. Mais qu'en est-il si l'on compte en binaire ?
Un doigt tendu vaut 1, et un doigt plié vaut 0.
Jusqu'où peut-on compter avec huit doigts maintenant ?
Les valeurs numériques ont une autre utilité très importante : elles permettent de créer des circuits logiques, qui prennent des décisions selon que certains fils présentent une tension élevée ou basse.
Une tension élevée est généralement considérée comme « vraie », et une tension basse comme « fausse ».
Si ces fils sont associés à des questions simples de type vrai ou faux et que les tensions sont les réponses, on peut alors considérer la sortie d'un circuit logique comme une conclusion obtenue après avoir posé une série de questions.
La logique permet de créer des circuits mathématiques, comme additionner deux nombres, ou des circuits qui ne fonctionnent que sous certaines conditions, comme une serrure qui ne s'ouvre que si l'on saisit la bonne combinaison de chiffres.
À la section suivante Des circuits qui font des choix, je vous présenterai quelques-uns des éléments constitutifs de la logique numérique et comment les utiliser pour créer des circuits intelligents.