Mathématiques de dessin Partie 1
Voir Aussi Mathématiques de dessin Partie 2
Introduction
Depuis la nuit des temps, l'homme a toujours voulu mesurer le monde qui l'entoure, mais ses compétences en matière de mesure ont souvent varié au cours de sa longue histoire.
A l'époque de l'homme des cavernes, par exemple, toutes les mesures étaient prises simplement en étirant les bras ou en comparant une certaine distance à la longueur de son pied ou de sa main.
Les mesures des mêmes distances variaient naturellement en fonction de la taille de l'homme. Bien que cette forme de mesure soit adaptée aux besoins de l'homme à cette époque, elle était inexacte.
L'une des premières mesures standard enregistrées a été développée par la civilisation des peuples vivant le long du Nil. Cette première mesure standard était appelée la coudée. Des traces de la coudée ont été retrouvées datant de 6000 av. J.-C.
Cette coudée était la distance entre l'avant-bras plié à la pointe du coude et le bout du doigt de la main tendue. Elle équivalait à environ 18 pouces.
Deux mille ans après le premier enregistrement de la coudée, elle a été fixée à exactement 18,24 pouces.
L'empan était utilisé pour les distances inférieures à une coudée. Cette distance équivalait à la mesure entre le bout du pouce et le petit doigt de la main tendue. Elle était égale à 9 pouces, soit une demi-coudée.
Une étude des dimensions des pyramides montre que toutes leurs mesures sont des multiples ou des fractions de la coudée.
L'industrie moderne exige des dimensions infiniment plus précises que celles utilisées pour construire les pyramides.
La plupart des objets que nous utilisons dans notre vie quotidienne ne pourraient pas être produits de manière économique sans l'utilisation de mesures précises. L'étude des mesures a beaucoup progressé depuis la construction des pyramides.
Il est maintenant possible de mesurer avec précision au millionième de pouce.
Les dessins des pièces de machines doivent être soigneusement dimensionnés. Le calcul des valeurs des dimensions représente une part surprenante du temps d'un dessinateur de machines.
La plupart des mathématiques qu'il utilise ne sont pas plus compliquées que l'utilisation ordonnée de processus arithmétiques relativement simples. Ces mathématiques consistent essentiellement à additionner, multiplier, soustraire et diviser, ainsi qu'à mettre au carré et à trouver les racines carrées de nombres.
Les mathématiques avancées requises par l'industrie moderne sont utilisées par des ingénieurs de conception et de développement spécialement formés.
Certains de leurs problèmes typiques incluent le calcul de la contrainte, des forces, des pressions et de la vitesse des pièces mobiles d'un produit.
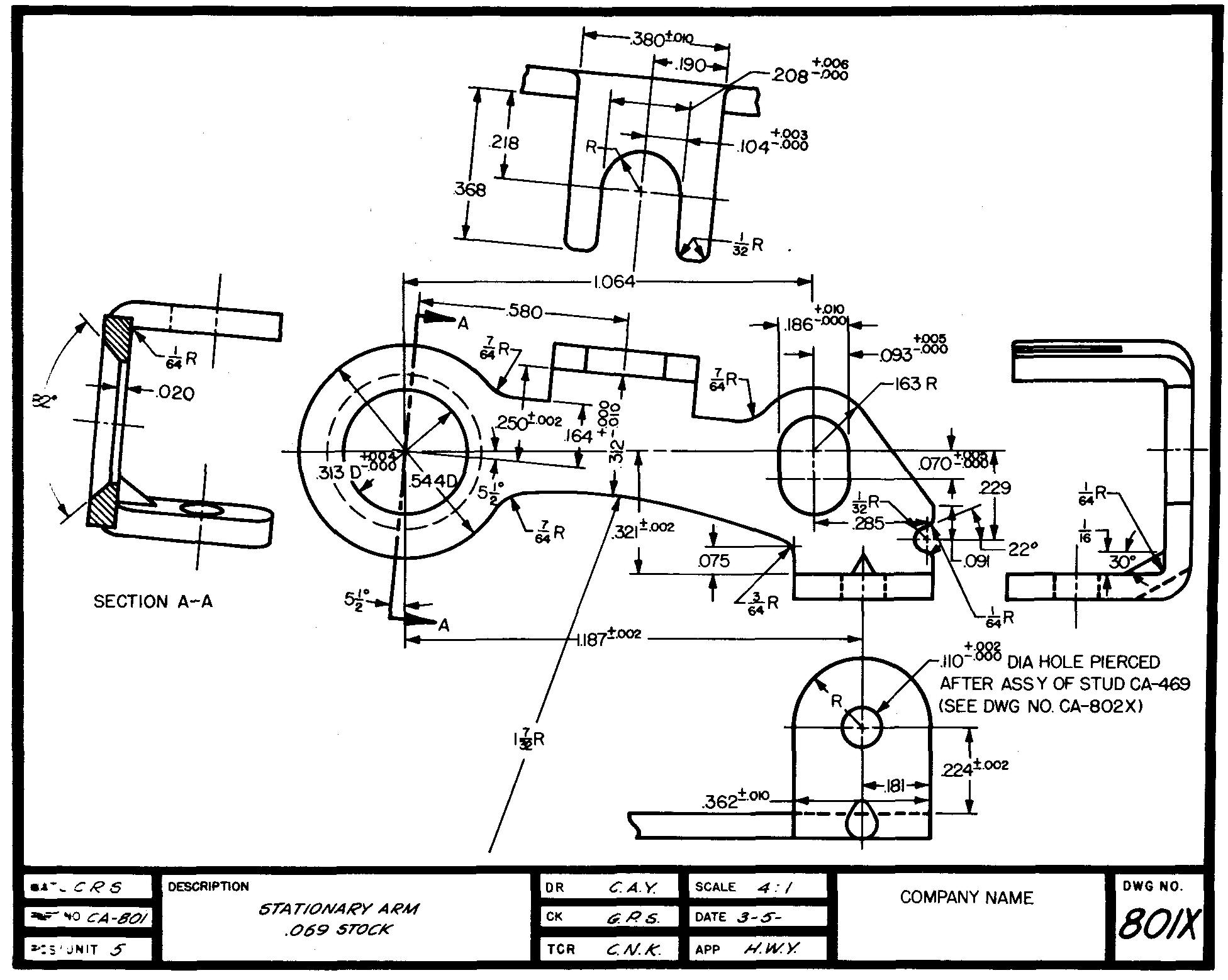
La figure 10-1 est un dessin détaillé d'une pièce de machine complexe.
Fig. 10-1. Une pièce de machine compliquée

Presque toutes les dimensions
indiquées sur le dessin ont été obtenues en utilisant des processus
arithmétiques de base.
Le dessinateur a commencé par sélectionner une échelle
de dessin appropriée (dans ce cas quatre fois la taille).
Pour vérifier l'adéquation de l'échelle, il a utilisé l'arithmétique qui impliquait de diviser, multiplier, additionner et soustraire des nombres. Il savait alors que les vues s'adapteraient parfaitement sur la feuille.
Avant de pouvoir dessiner les vues de cette pièce, le dessinateur a dû calculer les distances et les tailles de chacun des éléments de la pièce.
Une fois les vues dessinées, le dessinateur a utilisé ces calculs pour appliquer les dimensions aux dessins.
Le dessinateur doit penser à donner toutes les dimensions nécessaires à la réalisation de la pièce. L'ouvrier doit pouvoir réaliser la pièce à partir du dessin sans avoir à calculer lui-même les dimensions.
Lors de la préparation du dessin de la figure 10-1, le dessinateur a également déterminé l'emplacement des trous et des autres éléments de la pièce. Ils ont été soigneusement vérifiés pour éviter toute interférence entre un élément et un autre.
Le dessinateur a également dû utiliser l'arithmétique pour obtenir les informations nécessaires aux notes de perçage, d'alésage et de filetage.
Comme vous pouvez le constater, la connaissance des mathématiques de base est si importante pour le dessinateur de machines qu'il ne pourrait pas faire son travail sans elle.
Cette section illustrera certains des termes, formules et processus mathématiques les plus courants utilisés par les dessinateurs de machines dans leur travail. Des exemples pratiques sont donnés dans chaque cas, reliant les mathématiques à des situations de dessin spécifiques.
Résolution de problèmes
Il est important pour le dessinateur de machines de développer une procédure ordonnée pour résoudre les problèmes. La plupart des dessinateurs à succès commencent la résolution d'un problème en préparant un croquis à main levée, comme le montre la figure 10-2.
Fig. 10-2. Un croquis de problème
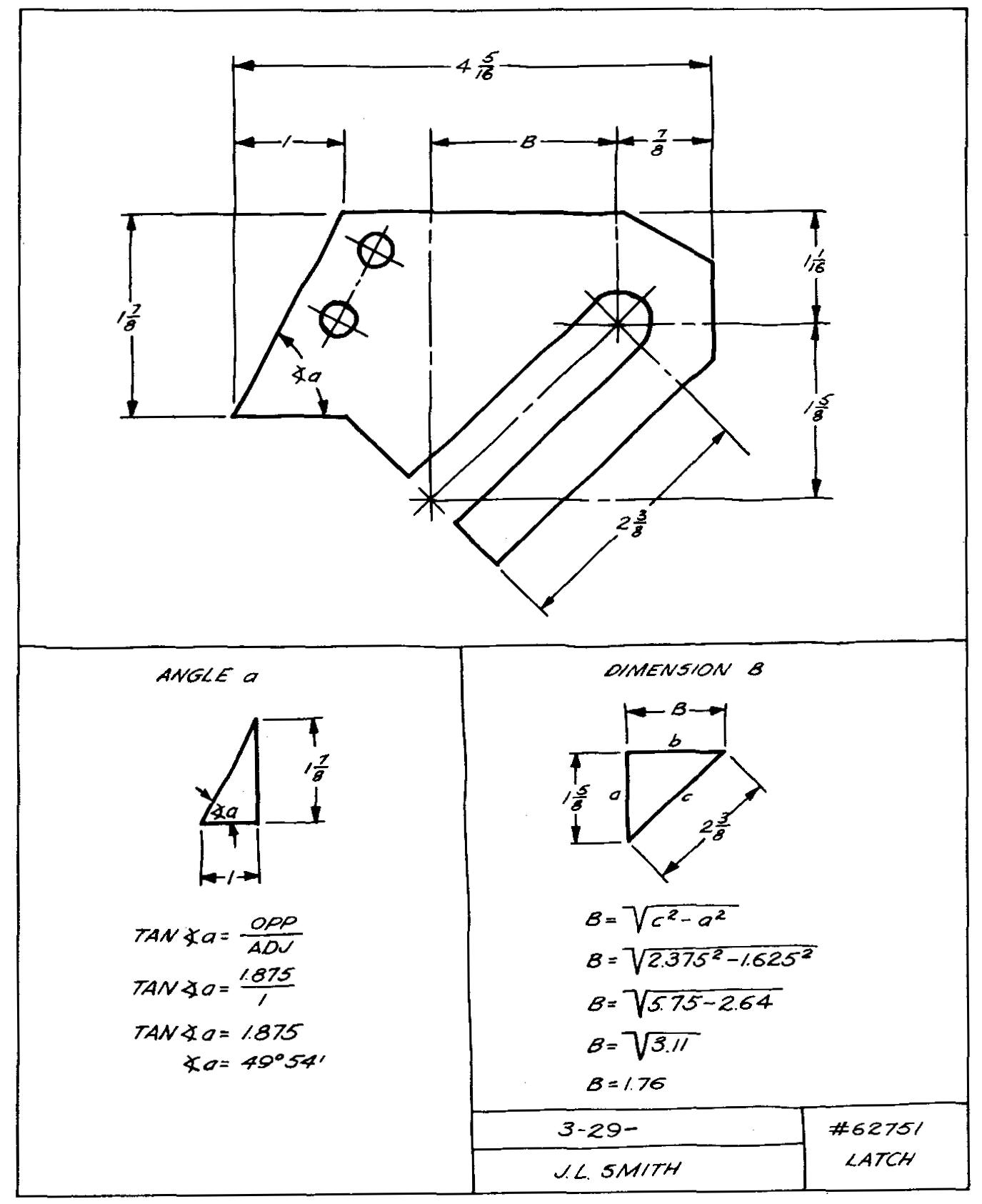
Sur ce croquis, le dessinateur peut montrer toutes les informations connues. Il peut relier ces informations aux facteurs qui sont inconnus au début de son travail (angle a et dimension B sur la Fig. 10-2).
Cette approche est appelée mise en place du problème. Dans certains cas, il peut être utile d'utiliser différentes couleurs de mine de crayon pour représenter les informations requises sur le croquis.
Sur la feuille contenant le croquis, le dessinateur énumère toutes les formules nécessaires qu'il prévoit d'utiliser. Pour simplifier le travail, le dessinateur énumère chaque étape de son processus du début à la réponse finale. Cette liste aide le dessinateur à vérifier si une telle vérification devient nécessaire plus tard.
Un titre doit être ajouté au croquis, indiquant le nom et le numéro de la pièce, le nom du dessinateur et la date à laquelle le problème a été résolu.
Toute autre information appropriée doit également être indiquée.
La plupart des entreprises fournissent aux dessinateurs des blocs de papier de 8-1/2 pouces sur 11 pouces pour résoudre les problèmes. Le papier peut être uni, à lignes régulières ou à lignes pour graphiques.
Une fois que tous les dessins d'une machine ou d'une structure sont terminés, ils sont soigneusement inspectés par un dessinateur ou un ingénieur expérimenté, appelé vérificateur. Chaque ligne, note et dimension est ainsi vérifiée deux fois pour en vérifier l'exactitude.
Il est judicieux pour le dessinateur de conserver ses figures et ses croquis jusqu'à ce que les dessins définitifs aient été vérifiés et envoyés à l'atelier. La sauvegarde des figures permet de s'y référer si le vérificateur découvre une erreur ou s'il a des questions à leur sujet.
Les vérificateurs souhaitent souvent avoir une preuve des calculs de dessin. Les avantages obtenus en sauvegardant les calculs ne peuvent être surestimés.
Changer les fractions en décimales
Pour résoudre des problèmes impliquant des nombres fractionnaires tels que 1/2, 29/32 et 3-5/16, il est souvent plus pratique de remplacer les fractions par leurs équivalents décimaux.
Cela peut être fait rapidement en utilisant le tableau illustré à la figure 10-3. Les nombres de 1/64 à 1 sont indiqués sur ce tableau avec leurs équivalents décimaux.
Fig. 10-3. Un tableau de conversion décimale
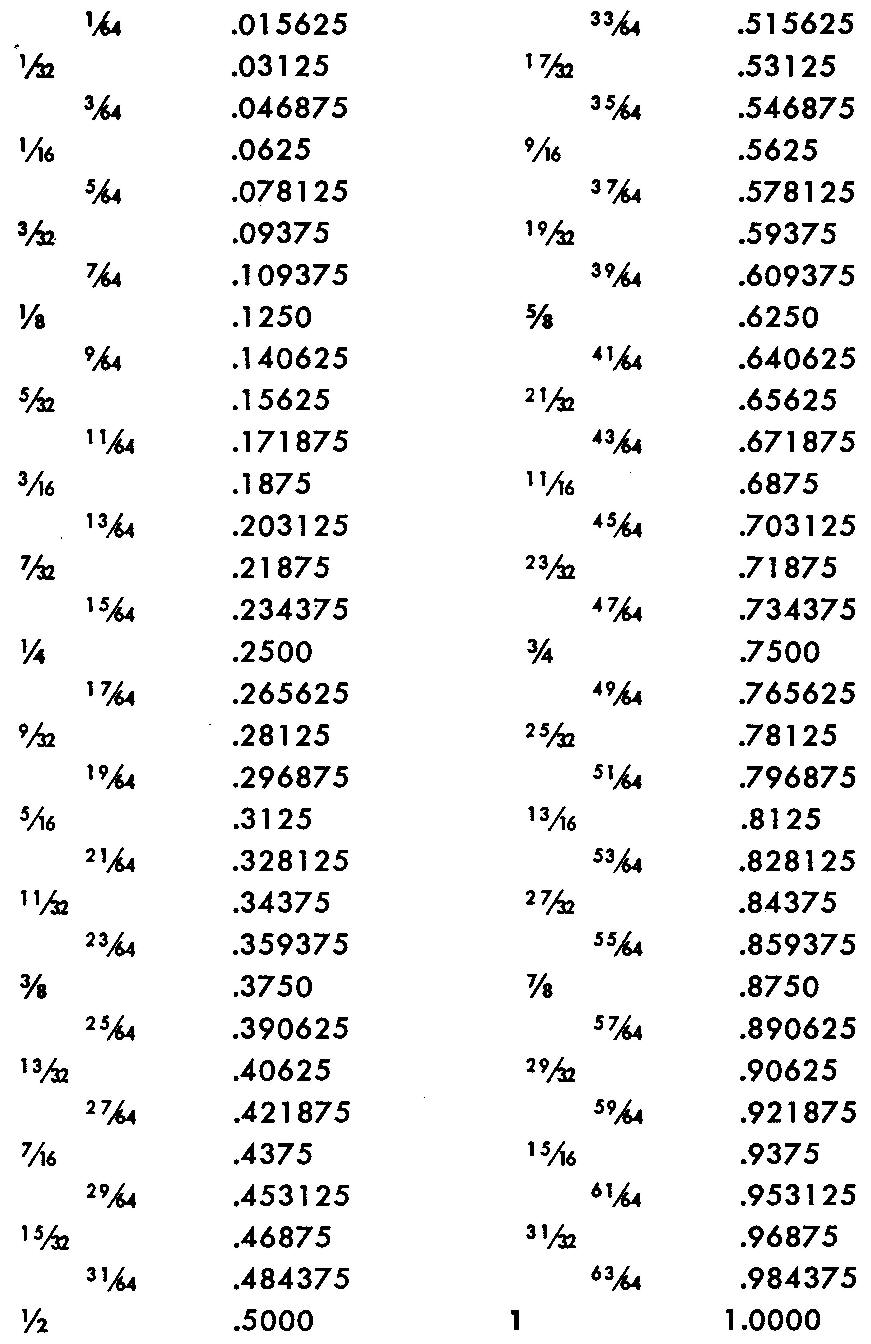
Une fraction courante peut être transformée en son équivalent décimal en divisant le numérateur de la fraction par le dénominateur. Par exemple, pour trouver l'équivalent décimal de 5/8, divisez 5 par 8.
La réponse est 0,625.
Exemple
Trouvez l'équivalent décimal pour chacun des éléments suivants :
a. 1/2 pouce. b. 2-3/4 pouces,
c. 7/8 pouces. d. 11-3/16 pouces,
e. 19/32 pouces. f. 6-15/64 pouces.
Solution
Pour a, trouvez la fraction 1/2 dans la première colonne de la figure 10-3. Lisez vers la droite pour trouver l'équivalent décimal.
a. 1/2 pouce = 0,5000 pouce.
Pour b, trouvez la fraction 3/4 dans la figure 10-3 et lisez vers la droite pour trouver l'équivalent décimal. Puisque 2-3/4 pouces incluent le nombre entier 2, le 2 doit être inclus dans l'équivalent décimal.
Les équivalents décimaux des fractions données dans l'exemple sont :
b. 2-3/4 pouces = 2,7500 pouces.
c. 7/8 po = 0,8750 po
d. 11-3/16 po = 11,1875 po
e. 19/32 po = 0,59375 po
f. 6-15/64 po = 6,234375 po
Travailler avec des constantes
Certaines valeurs connues et immuables, appelées constantes, simplifient l'arithmétique de nombreuses formules.
Les constantes ne sont utilisées que pour les figures géométriques régulières ou proportionnelles telles que les triangles, les carrés, les rectangles et les cercles.
Par exemple, dans le triangle équilatéral illustré à la figure 10-4, notez que l'altitude est donnée comme étant égale à 0,866s.
Fig. 10-4. Un triangle équilatéral
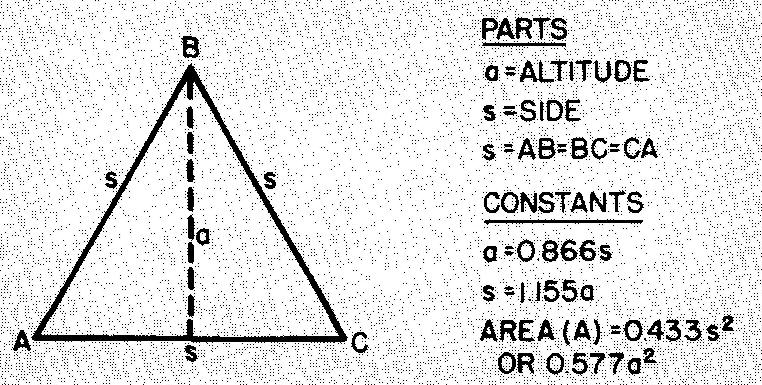
Cela signifie que chaque triangle équilatéral, quelle que soit sa taille, a une altitude égale à 0,866 fois ou 86,6 pour cent de la mesure d'un côté de ce triangle.
La plupart des exemples qui
suivent utilisent des constantes comme raccourcis pour résoudre les parties
inconnues de diverses figures régulières.
Triangles équilatéraux
Le triangle équilatéral, une figure régulière avec trois côtés égaux et trois angles égaux de 60°, est représenté sur la figure 10-4.
La figure 10-4 donne également quelques formules pour le triangle équilatéral. Notez l'utilisation de constantes dans ces formules.
Exemple de dimensions de filetage
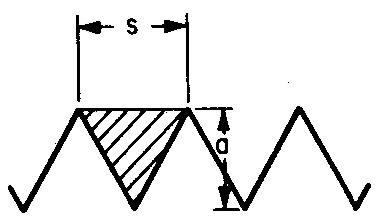
Quelle est la profondeur du filetage pour le filetage 1/4-20 NC représenté sur la figure 10-5 ?
fig. 10-5.
Solution
a = profondeur du filetage, s = pas du filetage. Pour 20 filetages par pouce, le pas (s) est égal à 1/20 de pouce, soit 0,05 pouce.
Comme le montre la figure 10-4, a = 0,866 S.
En remplaçant s par 0,05 :
a = (0,866) (0,05), ou 0,866 fois 0,05.
a = 0,0433 po.
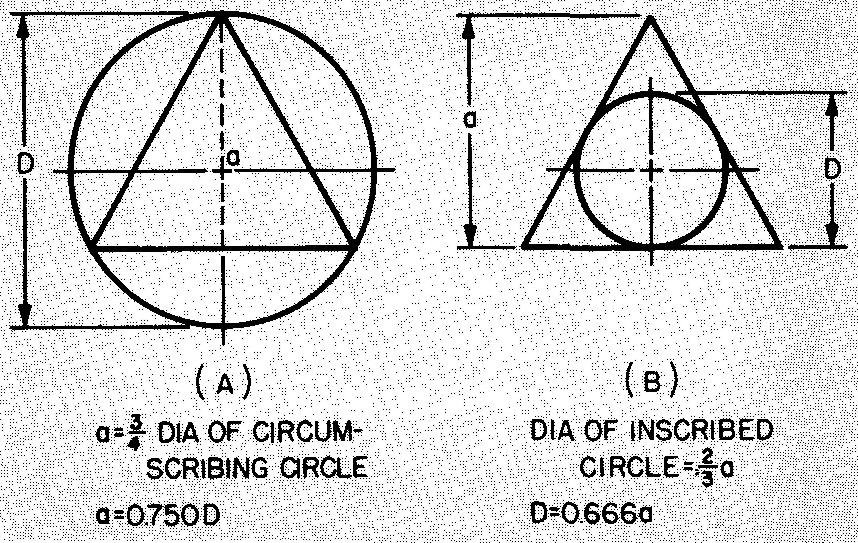
Relations entre triangle équilatéral et cercle
Les relations entre les
triangles équilatéraux et certains cercles sont illustrées dans la figure 10-6.
Fig. 10-6. Relations entre les triangles équilatéraux et les cercles
Exemple 1 : dimensionnement des trous de boulons
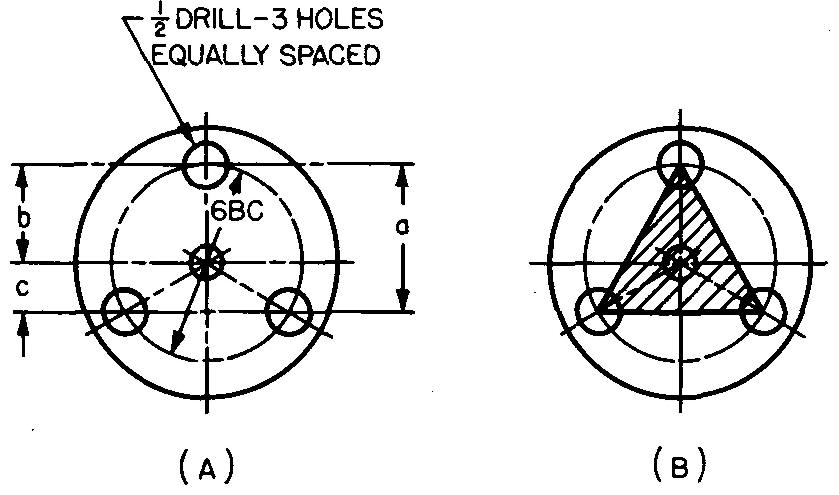
Calculez les dimensions a, b et c dans la Fig. 10-7 A.
Fig. 10-7.
Solution
Les lignes tracées reliant les centres des trois trous espacés de manière égale sur un cercle de boulons forment un triangle équilatéral, comme illustré dans la Fig. 10-7B.
ÉTAPE 1 : Comme illustré dans la Fig. 10-6, a = 0,75D.
En remplaçant D par 6 (donné dans la Fig. 10-7A) : a = (0,75) (6). a = 4,5 po.
ÉTAPE 2 : Comme illustré dans la Fig. 10-7, b = 6/2. b = 3 po. ÉTAPE 3 : Comme illustré dans la Fig. 10-7, c — a — b.
En remplaçant a par 4,5 (ÉTAPE 1) et b par 3 (ÉTAPE 2) : c = 4,5 - 3. c = 1,5 po.
Exemple 2 : dimensionnement d'un dessin
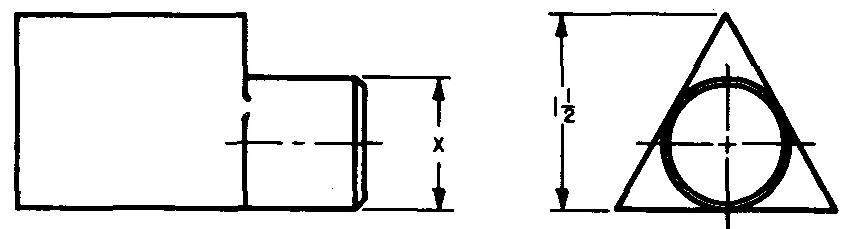
Calculez la dimension x dans la Fig. 10-8.
Fig. 10-8.
Solution
Comme le montrent les figures 10-6 et 10-8, D = 0,666a et D = x.
En remplaçant x par D : x = 0,666a.
Comme le montre la figure 10-8, a = 1,5 po.
En remplaçant 1,5 par a : x= (0,666) (1,5). x = 0,999 po.
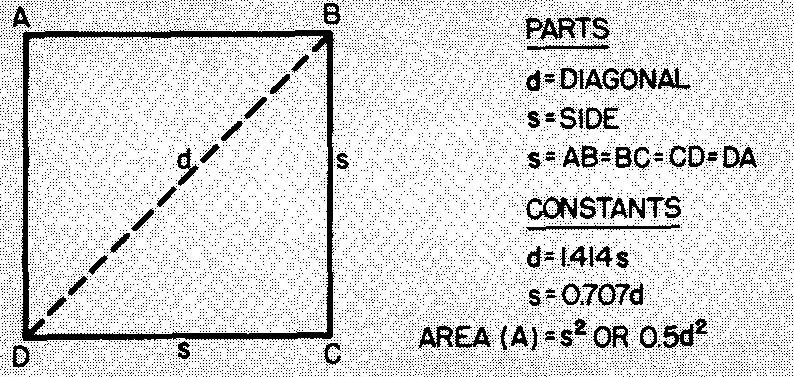
Les Carrés
Un carré est un rectangle à quatre côtés égaux. (Un rectangle est une figure à quatre côtés avec des angles de 90°.)
La figure 10-9 donne quelques formules pour les carrés.
Fig. 10-9. Un carré
exemple 1 calcul du jeu d'angle pour un écrou carré
Quelle est la distance entre les angles de l'écrou carré illustré à la Fig. 10-10 ?
Fig. 10-10.
Solution
Comme le montre la figure 10-9, d = 1,4145.
En remplaçant s par 1,0625 (donné dans la figure 10-10) : d = (1,414)(1,0625). d = 1,502 po.
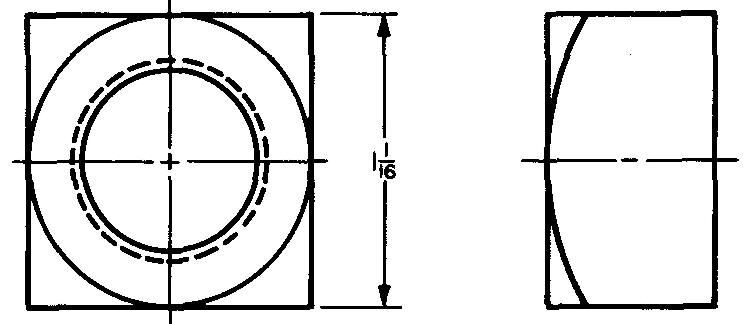
Exemple 2 : dimensionnement d'un dessin
Calculez la dimension x dans la Fig. 10-11.
Fig. 10-11.
Solution
Comme le montre la Fig. 10-9, d = 1,414s.
En remplaçant s par 0,75 (donné dans la Fig. 10-11) :
d= (1,414) (0,75). d = 1,061 po.
Hexagones
Les figures avec six côtés égaux et six angles égaux de 120° sont appelées hexagones réguliers.
La figure 10-12 donne quelques formules pour les hexagones. Un hexagone régulier peut être divisé en six triangles équilatéraux égaux (ou congruents) comme indiqué dans la figure 10-13.
Fig. 10-12. Un hexagone
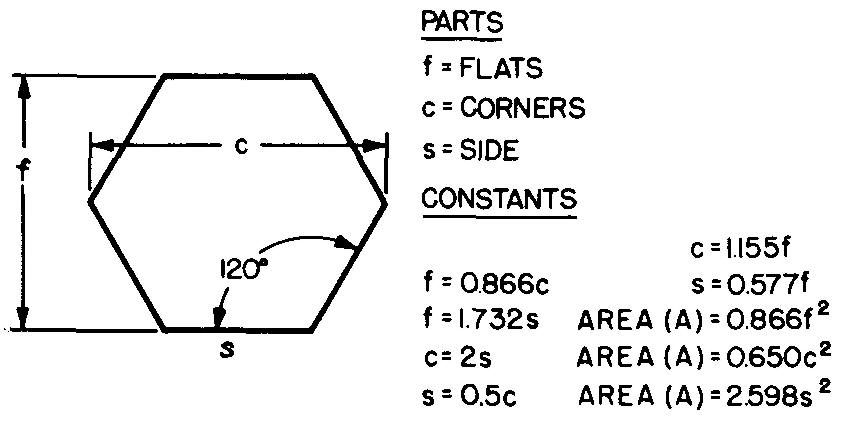
Fig. 10-13
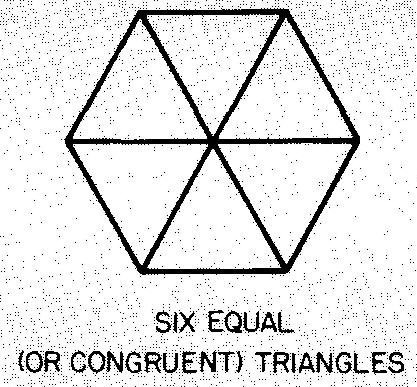
Exemple 1
dimensionnement des trous de boulons
Dans la figure 10-14A, six trous de boulons sont également espacés sur un cercle de boulons de 6 pouces de diamètre. Calculez les dimensions s et x.
Fig. 10-14
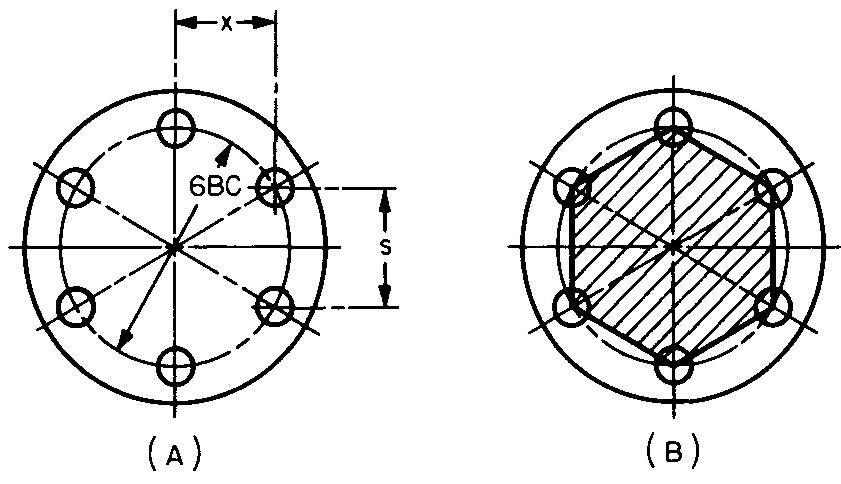
Solution
Les lignes reliant les centres des six trous adjacents également espacés sur un cercle de boulons forment l'hexagone ombré illustré dans la figure 10-14B.
ÉTAPE 1 : Comme indiqué dans la figure 10-12 : 5 = 0,5c.
En remplaçant c par 6 (donné dans la Fig. 10-14) : s=(0,5)(6). s = 3 po.
ÉTAPE 2 : La dimension x correspond à la hauteur d'un triangle équilatéral.
Comme le montre la Fig. 10-4, a = 0,866 s.
La Figure 10-14 donne x = a.
En remplaçant a par 0,866 s : x = 0,866 s.
En remplaçant s par 3 (de l'ÉTAPE 1) : x = (0,866) (3). x = 2,598 po.
Exemple 2 Calcul du jeu d'angle pour un écrou hexagonal
Quelle est la distance entre les angles de l'écrou hexagonal illustré à la Fig. 10-15 ?
Fig. 10-15
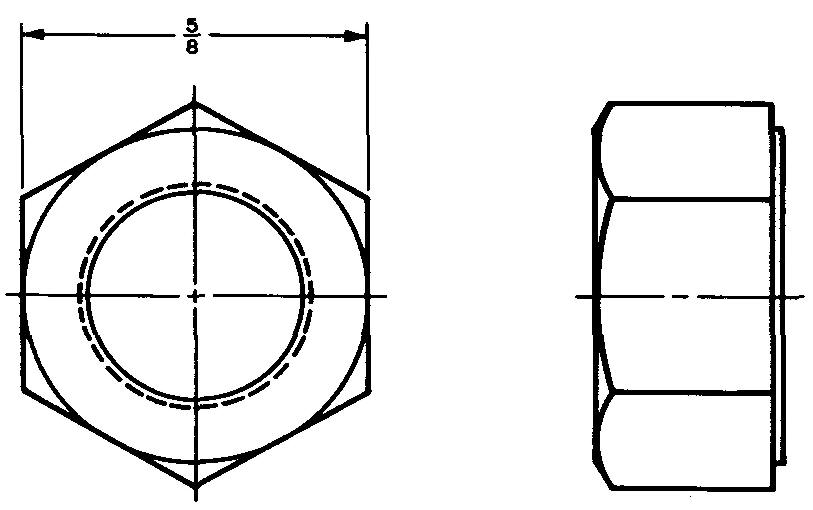
Solution
Comme le montre la Fig. 10-12, c = 1,155f.
En remplaçant 0,625 par / (donné à la Fig. 10-15) : c= (1,155)(0,625). c = 0,722 po.
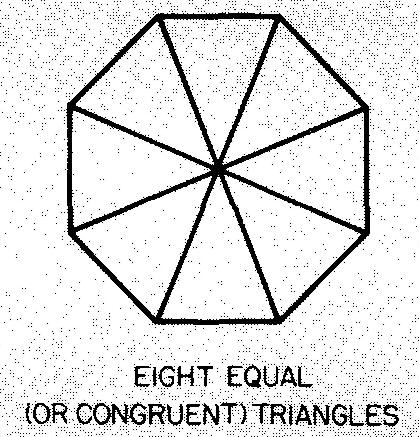
Octogones
Une figure avec huit côtés égaux et huit angles égaux de 135° est appelée octogone régulier. La Figure 10-16 donne les formules de l'octogone. Un octogone régulier peut être divisé en huit triangles égaux (ou congruents) comme le montre la Fig. 10-17.
Fig. 10-16. Un octogone
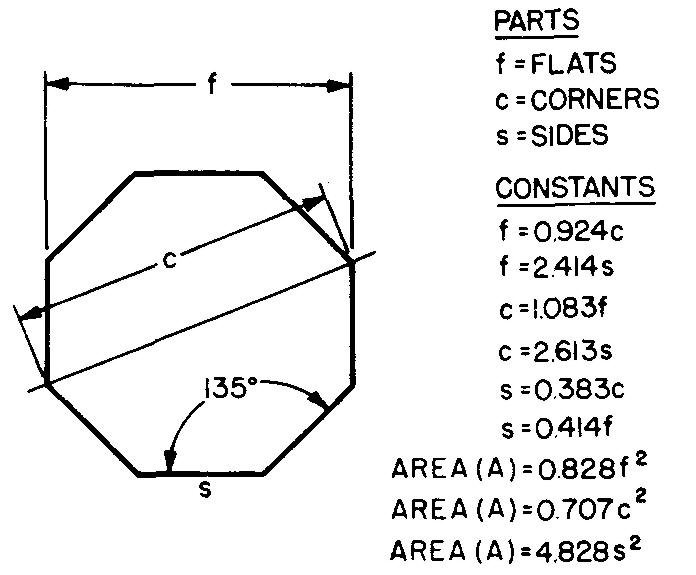
Fig. 10-17
Exemple 1 : dimensionnement d'un dessin
Un octogone doit être découpé dans un morceau de bois carré de 3-3/4 pouces comme indiqué sur la figure 10-18. Résolvez la dimension x.
Fig. 10-18
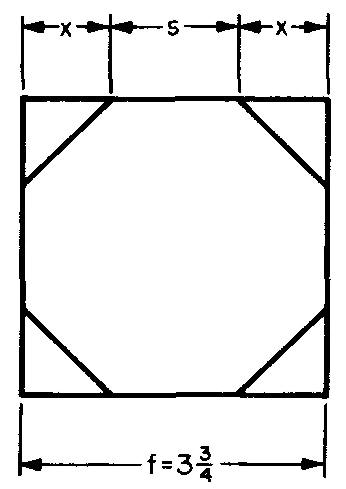
Solution
ÉTAPE 1 : Comme le montre la Fig. 10-16, s = 0,414f. En remplaçant f par 3,75 (donné dans la Fig. 10-18) :
s= (0,414) (3,75).
s= 1,553 po.
ÉTAPE 2 : Comme le montre la Fig. 10-18, f — s = 2x.
En remplaçant / par 3,75 (donné
dans la Fig. 10-18) et s par 1,553 (de l'ÉTAPE 1) : X = 3,75 - 1,553 / 2
x= 1,099 po.
Exemple 2 : dimensionnement des trous de boulons
Calculez les dimensions f, a et s et l'angle b dans la Fig. 10-19.
Fig. 10-19.
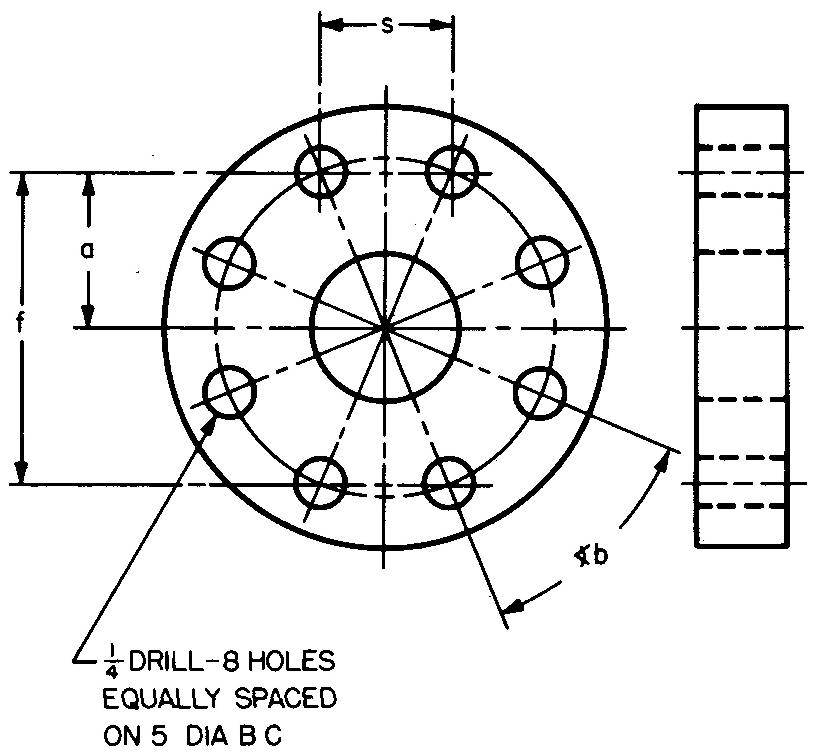
Solution
La note dessinée sur les trous de la Fig. 10-19 indique qu'il y a huit trous équidistants. Les lignes tracées reliant les centres des huit trous forment un octogone.
Les trous opposés sont espacés de 5 pouces. (Le cercle de boulons a un diamètre de 5 pouces.)
Cela représente c dans la Fig. 10-16. ÉTAPE 1 : Comme indiqué dans la Fig. 10-16, / = 0,924c.
En remplaçant c par 5 (donné dans la Fig. 10-19) : f= (0,924) (5).
f = 4,62 po.
ÉTAPE 2 : Comme indiqué dans la Fig. 10-19, a = f/2
En remplaçant f par 4,62 (de l'ÉTAPE 1) :
a = 4,62 / 2
f = 2,31 po.
ÉTAPE 3 : Comme indiqué dans la Fig. 10-16, s = 0,383c. En remplaçant c par 5 (donné dans la Fig. 10-19) : 5= (0,383)(5). s = 1,915 po.
ÉTAPE 4 : L'angle b mesure l'espacement angulaire entre les trous adjacents.
Il y a huit trous espacés de manière égale sur un cercle. Un cercle contient 360°.
Par conséquent
<b = 360° / 8 = 45°.
Trigonométrie
Les techniques de trigonométrie peuvent être utilisées pour trouver la mesure des côtés et des angles des triangles.
La trigonométrie est un outil extrêmement précieux pour le dessinateur de machines, car un grand nombre de problèmes de dessin et d'atelier peuvent être résolus en appliquant des relations trigonométriques.
Remarquez comment nous continuons à utiliser l'arithmétique de base pour résoudre les problèmes trigonométriques dans les exemples suivants de problèmes de dessin.
Nous allons discuter des problèmes qui ne concernent que le triangle rectangle. Un triangle rectangle a toujours un angle de 90°. Remarquez les termes qui décrivent chaque côté du triangle dans la figure 10-20A.
Fig. 10-20. Un triangle rectangle
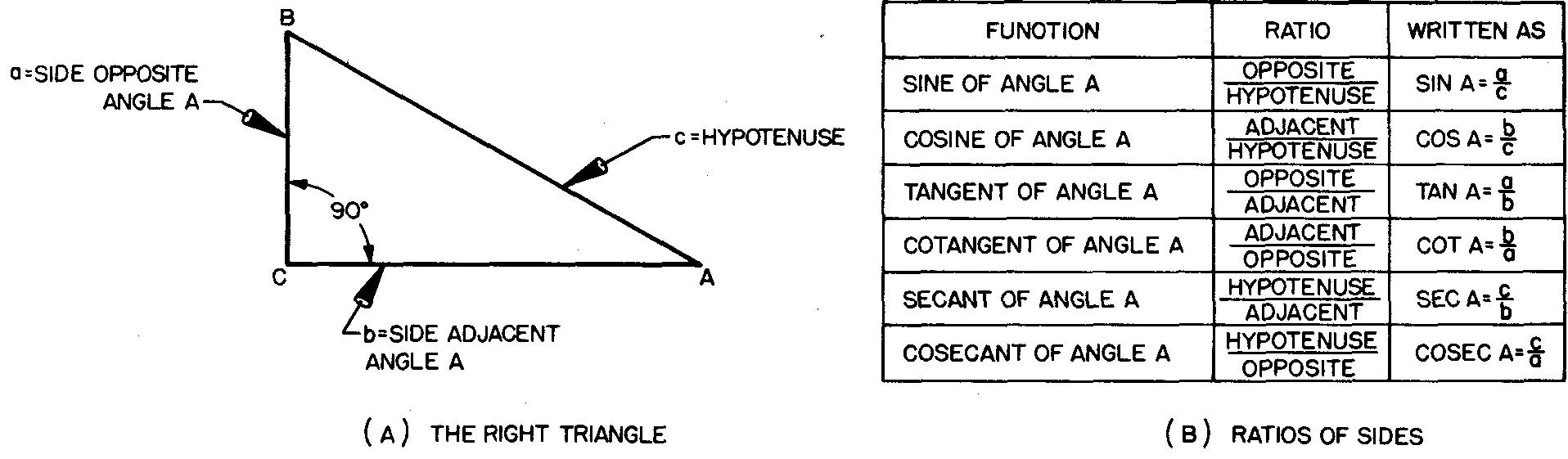
Le côté a est opposé à l'angle A et le côté b est adjacent à (le long du côté de) l'angle A. Le côté c est appelé l'hypoténuse. L'hypoténuse est toujours le côté le plus long d'un triangle rectangle. Les côtés formant l'angle droit sont appelés jambes.
Étant donné que la somme des mesures des trois angles d'un triangle est toujours de 180°, il est possible de trouver la mesure de l'un ou l'autre angle aigu (angle A ou angle B) si la mesure de l'autre angle est connue. Dans un triangle rectangle, l'angle C mesure 90°.
Par conséquent, la somme des angles A et B totalise toujours 90°. Ainsi, si l'angle B est connu pour être de 60°, l'angle A est de 30°.
Chacun des trois côtés d'un triangle peut être lié à chacun des autres côtés sous forme de rapport. Un rapport est une comparaison de deux nombres.
Dans les rapports de mesures, les nombres comparés doivent mesurer des éléments similaires tels que la vitesse, le temps ou les côtés d'un triangle.
Pour tout triangle, il existe six rapports possibles. Pour les triangles rectangles, les six rapports sont déterminés à partir de la taille de l'angle A. Ces rapports sont répertoriés dans la figure 10-20B.
Chaque rapport est appelé une fonction trigonométrique de l'angle A. Lorsque la mesure de l'angle A change, la valeur de chaque fonction trigonométrique change également.
Dans un triangle rectangle, la mesure de l'angle A doit être supérieure à 0° et inférieure à 90°. L'angle A peut être n'importe quelle mesure entre ces deux valeurs. Les mathématiciens ont élaboré avec précision un tableau de constantes pour les rapports des côtés des triangles rectangles pour chacun de ces angles.
Ils ont calculé les valeurs des rapports pour tous les angles de 0° à 90°. Ces valeurs sont appelées fonctions trigonométriques naturelles. Elles se trouvent dans le tableau 2.
En examinant le tableau 2, vous verrez que chaque section du tableau donne les valeurs d'un ensemble d'angles complémentaires.
C'est-à-dire que l'angle indiqué en haut de cette section du tableau plus l'angle indiqué en bas de cette section plus les 60 minutes répertoriées sur les bords de cette section du tableau sont égaux à 90°.
Vous remarquerez également que les noms des fonctions occupent des positions différentes en haut et en bas de chaque colonne.
De même, les minutes sont dans
l'ordre inverse de haut en bas sur les côtés droit et gauche de chaque section
du tableau.
Les informations fournies par ce tableau diffèrent selon que vous
lisez les colonnes de haut en bas ou de haut en bas.
Il est important de savoir dans quel sens lire. Il est également important de s'assurer que les titres de tableau utilisés donnent les informations pour le sens dans lequel le tableau a été lu.
Les exemples suivants clarifieront l'utilisation et la lecture du tableau 2.
Les relations entre les parties d'un triangle rectangle peuvent être utilisées pour trouver les mesures de toutes les parties d'un triangle rectangle donné à condition qu'un nombre minimum de faits soit connu.
Comme nous l'avons vu, nous pouvons trouver la mesure d'un angle aigu si la mesure de l'autre angle est connue. Si nous connaissons la mesure d'un côté et d'un angle aigu, nous pouvons résoudre les mesures des autres côtés.
Et si nous connaissons les mesures de deux côtés, nous pouvons trouver le troisième côté et les deux angles aigus.
Nous avons appris que les dimensions sur les dessins de détail doivent être calculées avec précision par le dessinateur de machines. Les exemples suivants illustrent les utilisations pratiques typiques de la trigonométrie pour calculer ces dimensions.
En examinant les exemples, essayez de voir comment l'application d'un triangle rectangle simplifie le problème.
La compétence du dessinateur dans l'application de la trigonométrie aux dessins de machines dépend de sa capacité à décomposer les problèmes en triangles rectangles, de sorte que les différentes parties de chaque zone puissent être plus facilement observées et résolues.
Exemple 1 : calcul des angles
Calculez l'angle A dans la Fig. 10-21.
Solution
La Figure 10-21 donne les mesures des deux côtés du triangle.
Fig. 10-21.
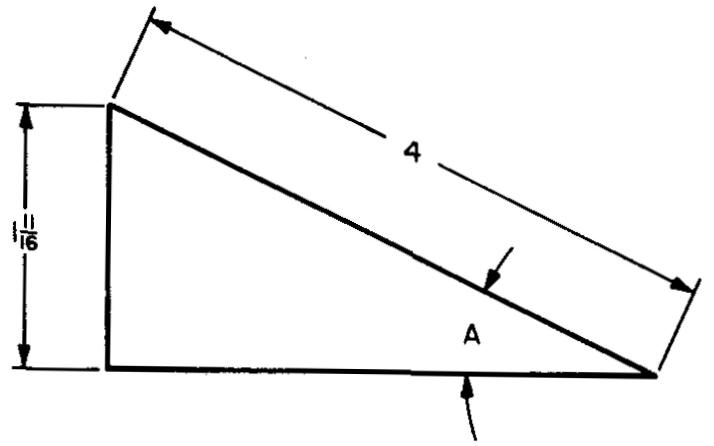
Nous connaissons le côté opposé (1,6875 po) et l'hypoténuse (4 po) et nous souhaitons trouver l'angle A.
À partir de la Fig. 10-20, nous sélectionnons un rapport impliquant les côtés a et c.
Nous pouvons utiliser soit le sinus, soit la cosécante.
Pour cet exemple, nous sélectionnerons le rapport sinus.
ÉTAPE 1 :
Comme le montre la Fig. 10-20, sin A = a/c.
En remplaçant a par 1,6875 et c par 4 (donné dans la Fig. 10-21) : sin A = 1,6875/4. sin .4 = 0,42188.
ÉTAPE 2 :
Pour trouver l'angle A, nous devons trouver le rapport calculé (ou le nombre le plus proche de sa valeur) dans le tableau 2, Fonctions trigonométriques naturelles.
En regardant sous les colonnes intitulées sin et cos, nous trouvons 0,42183 et 0,42209.
Étant donné que notre rapport calculé, 0,42188, est plus proche de 0,42183, nous utiliserons cette valeur comme notre rapport sinusoïdal.
Cette valeur a été intitulée sin en haut à gauche de cette section du tableau.
Nous prendrons donc comme mesure en degrés l'étiquette en haut à gauche, 24°, et nous lirons le côté gauche pour trouver les minutes.
Notre rapport sinusoïdal sélectionné, 0,42183, est opposé à 57'.
RÉSUMÉ :
Nous avons calculé sin A = 0,42188, ce qui correspond approximativement à 0,42183. sin 24°57' = 0,42183.
A = 24° 5 7', à la minute près.
Exemple 2 : trouver une branche d'un triangle rectangle
Calculez le côté a de la Fig. 10-22.
Fig. 10-22
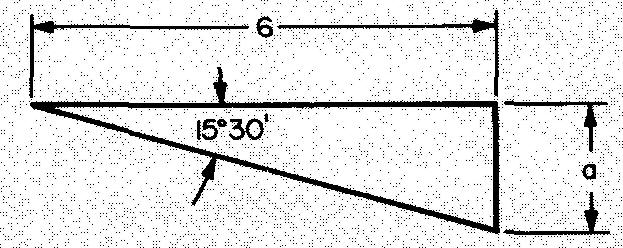
Solution
La Figure 10-22 donne la mesure de l'angle A et du côté b.
À partir de la Fig. 10-20, nous sélectionnons le rapport tangent. Nous allons résoudre le problème pour le côté a.
ÉTAPE 1 :
Comme indiqué sur la Fig. 10-20, tan A = a/b.
En remplaçant 15° 30' par < A et 6 par b (donné sur la Fig. 10-22) : tan 15°3O' = a/6. a= (tanl5°30')(6).
ÉTAPE 2 :
Trouvez tan 15°30' dans le Tableau 2.
Lisez la colonne vers le bas pour trouver 30' sur le bord gauche du tableau, puis en travers pour lire la valeur de 30' sous le coin supérieur droit, intitulé tan. tan 15°30' = 0,27732.
En remplaçant 0,27732 par tan 15°3O' dans l'équation de l'ÉTAPE 1 : a = (0,27732) (6). a = 1,664 po.
Exemple 3 application d'un triangle rectangle
Calculer la dimension x dans la Fig. 10-23.
Fig. 10-23
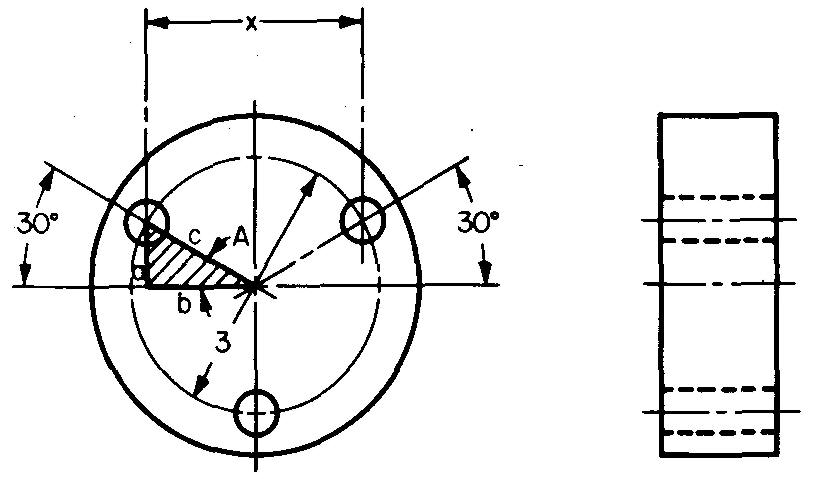
Solution
ÉTAPE 1 : La figure 10-23 donne c égal au rayon du cercle de boulons, ou c = 3/2.
c= 1,5 po.
ÉTAPE 2 : La figure 10-23 montre que x = 2b.
Pour trouver b, utilisez le rapport cosinus de la figure 10-20 :
cos A = b/c, ou b = (cos A) (c).
En remplaçant 30° par < A (donné dans la figure 10-23) et 1,5 par c (d'après l'ÉTAPE 1) : b= (cos30°)(1,5).
Dans le tableau 2, sous le titre en haut à gauche, cos, même avec le titre à gauche de 0', en lisant vers le bas, nous trouvons cos 30° = 0,86603, qui est substitué à cos 30° :
b= (0,86603) (1,5). b = 1,299 po.
ÉTAPE 3 :
La figure 10-23 donne x = 2b.
En remplaçant b par 1,299 (de l'ÉTAPE 2) : x= (2) (1,299). x = 2,598 po.
Exemple 4 : application d'un triangle rectangle
Calculez la dimension x dans la figure 10-24.
Fig. 10-24.
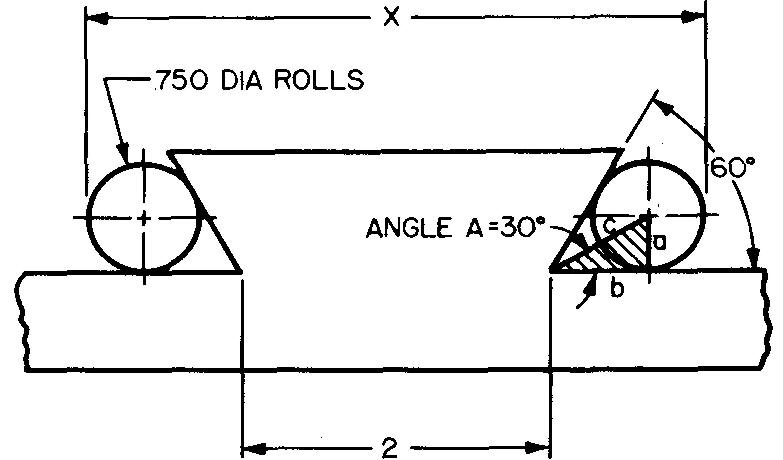
Solution
La dimension x est égale à 2 pouces plus 2 fois le côté b du triangle ombré illustré à la Fig. 10-24 plus 2 fois le rayon du rouleau.
ÉTAPE 1 :
À partir de la Fig. 10-24, nous avons a = le rayon du rouleau, soit 0,750 / 2, soit 0,375 pouces et A = la moitié de l'angle de 60°, soit 30°.
L'angle de 60° est divisé en deux par c.
À partir de la Fig. 10-20, nous sélectionnons le rapport cotangent : cot A = b/a.
En remplaçant A par 30° et a par 0,375 :
cot 30° = b / 0,375
b = (cot 30°) (0,375).
À partir du Tableau 2, en lisant vers le bas, nous trouvons cot 30° = 1,7320.
En remplaçant 1,7320 par cot 30° : b= (1,7320)(0,375). b = 0,650 po.
ÉTAPE 2 : x = 2 + 2b + 2r.
En remplaçant 0,650 par b et 0,375 par r. x = 2 + (2) (0,650) + (2) (0,375). x = 4,050 po.
Exemple 5 : application d'un triangle rectangle
Calculez l'angle de conicité dans la Fig. 10-25.
Fig. 10-25
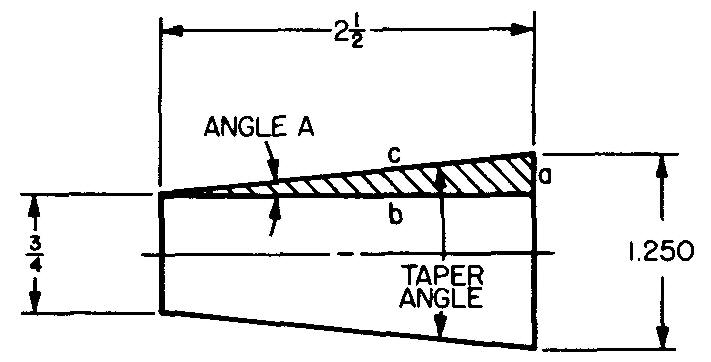
Solution
L'angle de conicité est égal à 2 fois l'angle A du triangle ombré.
À partir de la Fig. 10-20, nous sélectionnons le rapport tangent : tan A = a/b
ÉTAPE 1 :
À partir de la Fig. 10-25, nous voyons que a est égal à la moitié de la différence entre 1,25 et 0,75.
a = (1,25 - 0,75) / 2 = 0,5 ' / 2 ou 0,25 po.
b = 2,5 (donné dans la Fig. 10-25).
En remplaçant : tan A = 0,25 / 2,5
tan A = 0,10000.
En recherchant dans le Tableau 2 la valeur de tangente la plus proche de 0,10000, nous trouvons 0,09981 et 0,10011.
Notre valeur calculée, 0,10000, est plus proche de 0,10011.
Nous sélectionnons les valeurs de l'angle en haut et à gauche du tableau.
A = 5°43'.
ÉTAPE 2 : T = 2(A).
En remplaçant A par 5 °43' :
T= (2)(5°43') ou 11°26'.
Exemple 6 triangle rectangle
Calculez l'angle du cône primitif de l'engrenage représenté sur la figure 10-26.
Fig. 10-26.
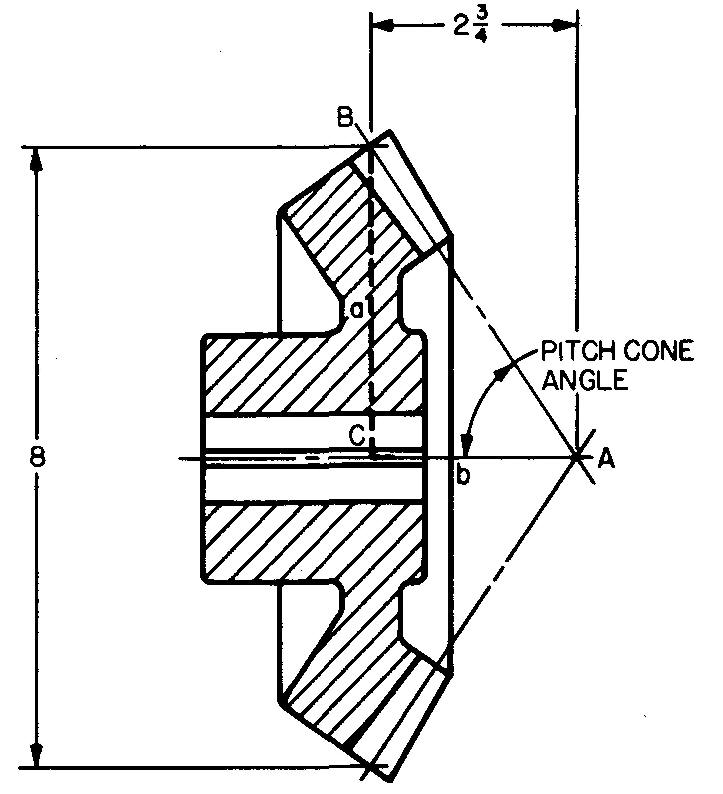
Solution
L'angle du cône primitif est égal à l'angle A du triangle ACB.
D'après la Fig. 10-26, nous voyons que le côté a = 8/2, ou 4, et b = 2,75.
D'après la Fig. 10-20, nous sélectionnons le rapport tangent : tan A = a/b.
En remplaçant : tan A = 4 / 2,75
tan A = 1,4545.
En regardant dans le Tableau 2 sous les colonnes étiquetées tan, nous trouvons 1,4541 et 1,4550. Notre rapport calculé est plus proche de 1,4541.
Nous sélectionnons les valeurs de l'angle des côtés inférieur et droit du tableau, opposés à 1,4541, en lisant les minutes en partant du bas.
A = 55°29'.
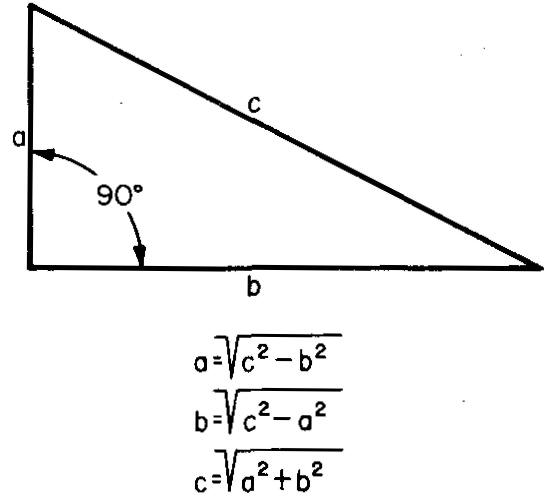
Résolution des côtés des triangles rectangles
Dans certains problèmes impliquant des triangles rectangles, ni l'angle A ni l'angle B ne sont connus. Il est possible de résoudre ces triangles en utilisant des relations trigonométriques comme indiqué dans la section ci-dessus.
Cependant, il est souvent plus simple d'utiliser l'arithmétique pour trouver un côté d'un triangle lorsque les deux autres côtés sont connus. Cette méthode plus courte utilise les formules de la figure 10-27.
Fig. 10-27
Exemple de recherche de dimensions pour les centres de poulies
Calculez la dimension c sur la Fig. 10-28.
Fig. 10-28.
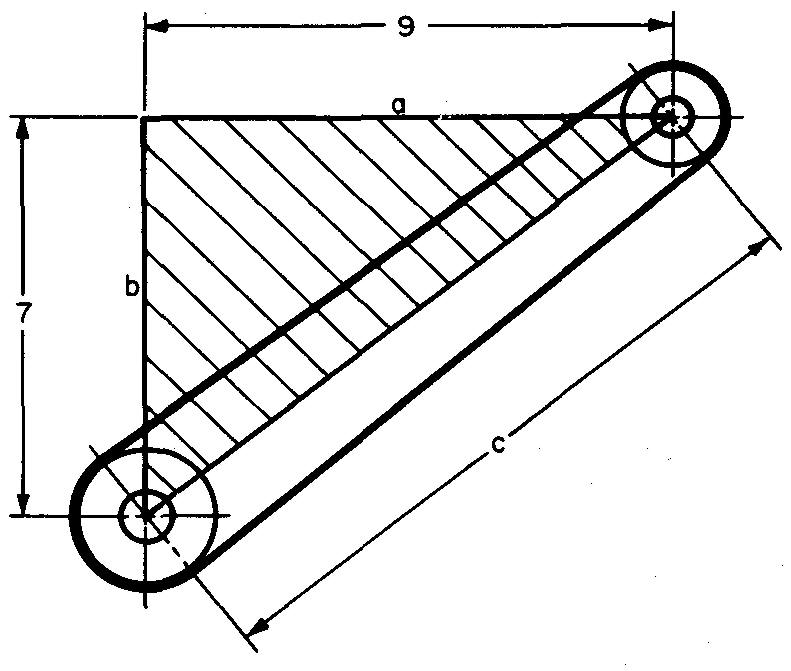
Solution
À partir de la Fig. 10-27, c = √(a2 + b2)
En remplaçant a par 9 et b par 7 (donné dans la Fig. 10-28) :
c = √(92 + 72)
À partir du Tableau 3, Fonctions des nombres, trouver la racine carrée de 130. c= 11,4018 pouces.
Résolution de l'aire des triangles rectangles
L'aire est la mesure de la surface délimitée par une figure fermée.
Les mesures d'aire standard incluent les pouces carrés et les pieds carrés. La figure 10-29 donne la formule pour trouver l'aire des triangles rectangles lorsque les mesures de deux côtés sont connues.
Fig. 10-29.
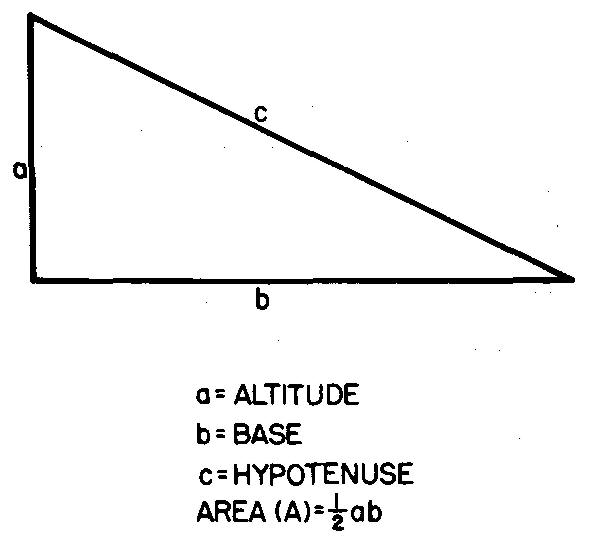
Exemple de
recherche de l'aire des triangles rectangles
Calculez l'aire d'un triangle rectangle dans lequel l'altitude = 1-1/4 pouces et la base = 2-1/2 pouces.
Solution
Comme le montre la figure 10-29, A = 1/2 ab.
En remplaçant 1,25 par a et 2,5 par b :
A = (1,25)(2,5) / 2 = 1,5625 po².
Triangles isocèles
Un triangle avec deux côtés égaux et deux angles égaux est appelé triangle isocèle.
La figure 10-30 montre que l'altitude divise le triangle isocèle en deux triangles rectangles égaux.
Fig. 10-30. Un triangle isocèle
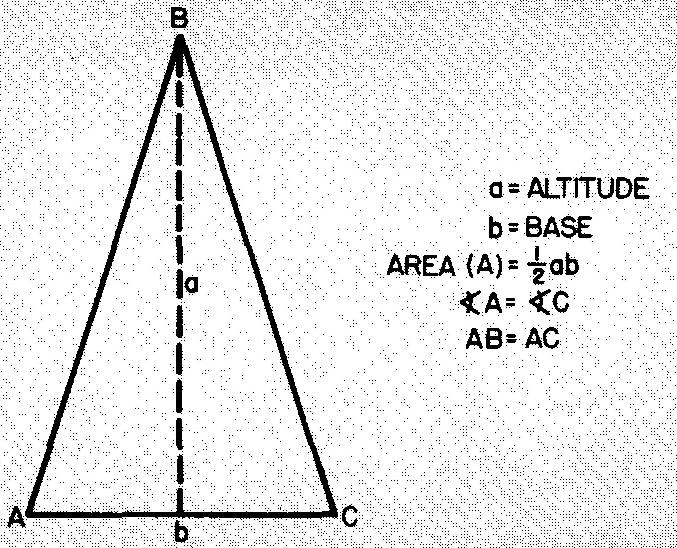
Exemple de calcul de l'aire de triangles isocèles
Calculez l'aire d'un triangle isocèle dont la base = 8 pouces et l'altitude = 10 pouces.
Solution
Comme le montre la figure 10-30, A = 1/2 ab.
En remplaçant a par 10 et b par 8 :
A = (10)(8) / 2 = 40 po².
Triangles scalènes ou obliques
Tout triangle ayant trois côtés inégaux est un triangle scalène. Les triangles rectangles scalènes peuvent être résolus comme indiqué.
Les formules pour d'autres triangles scalènes sont données dans la Fig. 10-31.
Fig. 10-31. un triangle scalène, ou oblique
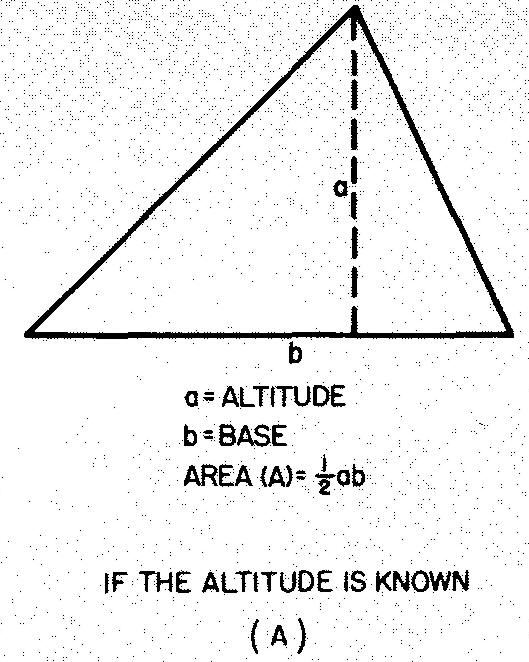
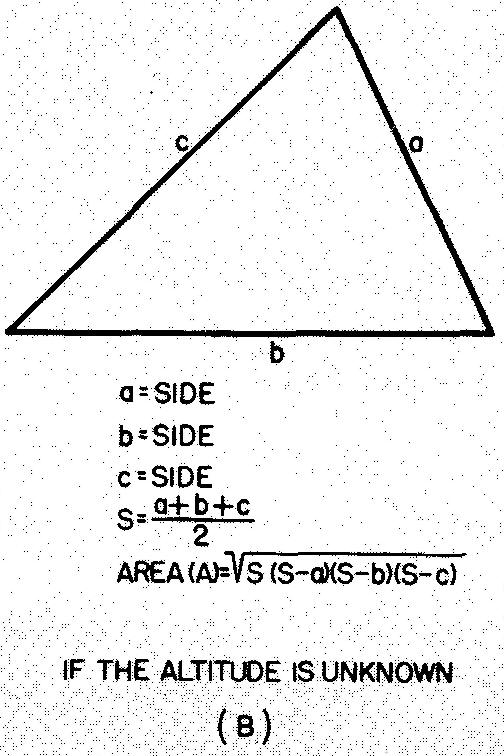
Exemple 1 : trouver l'aire des triangles scalènes
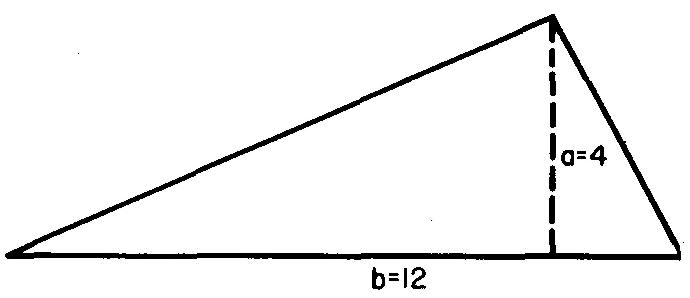
Calculer l'aire du triangle de la Fig. 10-32.
Fig. 10-32
Solution
Puisque l'altitude est connue, utiliser la formule de la Fig. 10-31 A : A = 1/2 ab.
En remplaçant 4 par a et 12 par b (donnée dans la Fig. 10-32) :
A = (4)(12) / 2 =24 pouces carrés.
Exemple 2 : trouver l'aire des triangles scalènes
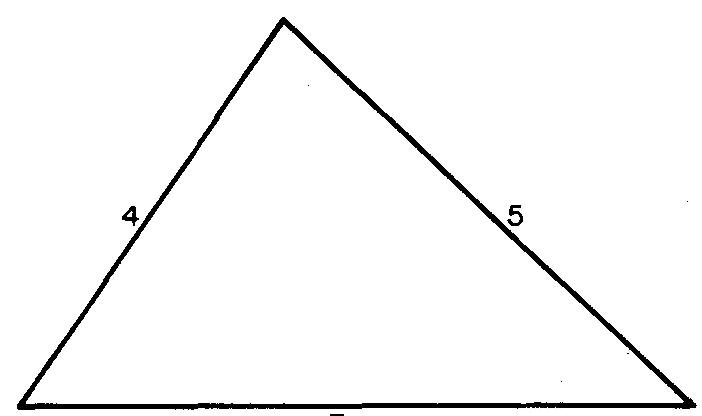
Calculer l'aire du triangle de la Fig. 10-33.
Fig. 10-33
Solution
Étant donné que l'altitude est inconnue, utilisez la formule de la Fig. 10-31B :
![]()
En remplaçant a
par 5, b par 7, c par 4 et 5 par 8 (données dans la Fig. 10-32). 5 est calculé à
partir de :
S = (a + b + c) / 2
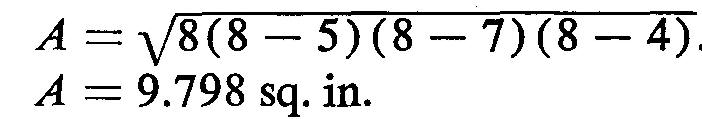
Trapèzes
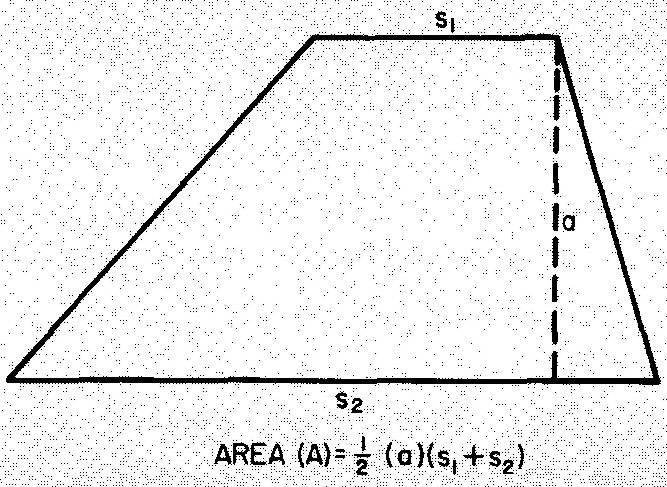
Les figures à quatre côtés avec deux et seulement deux côtés parallèles sont appelées trapèzes. La figure 10-34 donne la formule de l'aire des trapèzes.
Fig. 10-34. Un trapèze
Exemple de
recherche de l'aire des trapèzes
Solution
Comme le montre la figure 10-34
En remplaçant S1 par 8, S2 par 12 et a par 6
(donnée dans la figure 10-35) :
Fig. 10-35
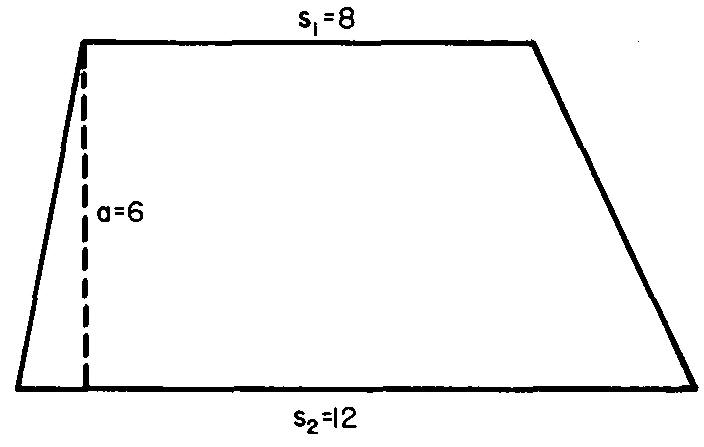
A = ((8 + 12)/2) x 6
A = 60 po².
