Mathématiques de dessin Partie 2

Dessin mécanique

Cercles

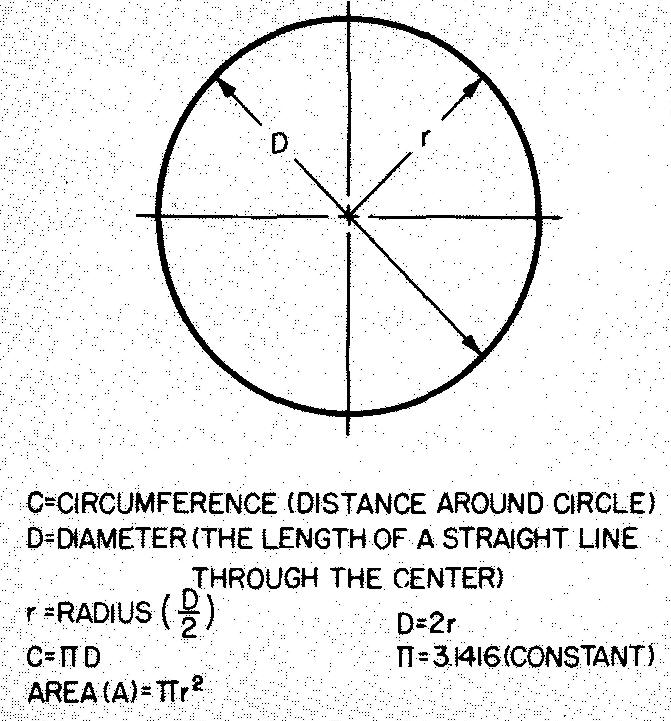
Un cercle est l'ensemble de tous les points sur un plan équidistants d'un point appelé le centre du cercle. Le centre du cercle se trouve dans la surface délimitée par le cercle.

La figure 10-36 donne les formules des cercles.

Fig. 10-36. Un cercle

Exemple 1 : trouver la circonférence d'une poulie

Calculez la circonférence d'une poulie d'un diamètre de 11-1/4 pouces.

Solution

Comme le montre la figure 10-36, C = πD

En remplaçant π par 3,1416 (donné dans la figure 10-36) et D par 11,25 :

C=(3,1416)(11,25) = 35,343 pouce

Exemple 2 : trouver l'aire délimitée par un cercle

Calculez l'aire d'une extrémité d'un réservoir cylindrique d'un diamètre de 14 pouces.

Solution

Comme le montre la figure 10-36,

A = = πr²

En remplaçant π par 3,1416 (donné dans la figure 10-36) et r par 7 calculé en divisant D par 2 ; D = 14 pouces, donc r = 7 pouces :

A = (3,1416) (72) = 153,9384 pouces carrés.

Arcs et secteurs

La figure 10-37 illustre un arc et un secteur d'un cercle. Un secteur est une partie de l'aire d'un cercle délimitée par un arc et par deux rayons.

Fig. 10-37. Un arc et un secteur

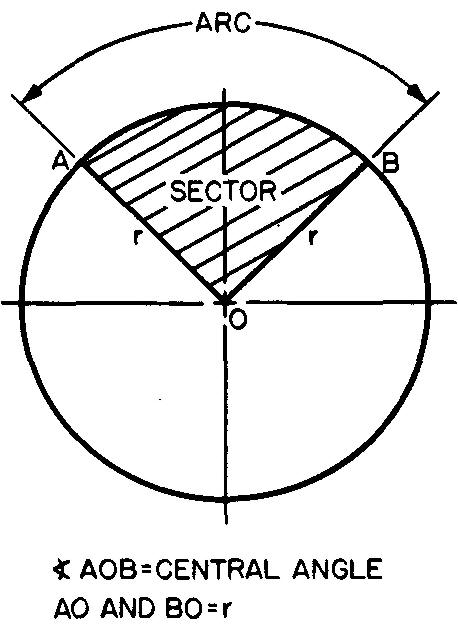
Un secteur peut être considéré comme une part de tarte. Il est mesuré par l'angle au centre, ou l'angle formé par les côtés droits de la tranche de tarte. Un arc est n'importe quelle portion d'un cercle. Un arc est mesuré par son angle au centre.

Exemple 1 : calculer la longueur d'un arc

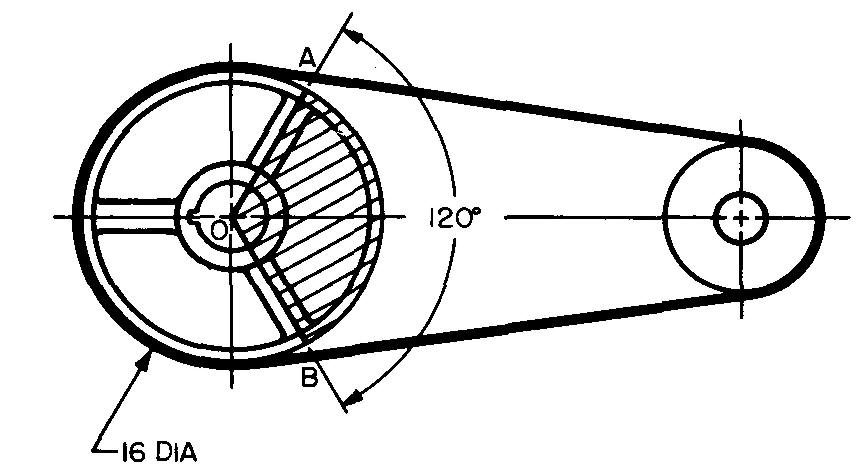
Calculez la longueur de l'arc AB de la partie ombrée de la grande poulie illustrée à la Fig. 10-38.

Fig. 10-38

Solution

ÉTAPE 1 :

Pour trouver la circonférence du cercle entier, utilisez C = πD de la Fig. 10-36.

En remplaçant π (donné à la Fig. 10-36) par 3,1416 et D par 16 (donné à la Fig. 10-38) :

C = (3,1416) (16) = 50,2656 po.

ÉTAPE 2 :

Trouvez la longueur de l'arc AB en pourcentage de la circonférence entière. La figure 10-38 donne une mesure de 120° pour l'arc AB.

Par conséquent, l'arc AB — 120/360 de la circonférence totale, soit 0,333 fois la circonférence du cercle.

AB = 120/360 C

En remplaçant C par 50,2656 (de l'ÉTAPE 1) :

AB = (0,333)(50,2656) = 16,738 po.

Exemple 2 : trouver l'aire des secteurs

Calculez l'aire du secteur ombré ABO dans la figure 10-38.

Solution

ÉTAPE 1 :

pour trouver l'aire du cercle entier, utilisez A = = πr² de la figure 10-36.

En remplaçant π par 3,1416 (donné dans la Fig. 10-36) et r par 8 (calculé à partir de la Fig. 10-38. D = 16 po, donc r = 8 po) :

A = (3,1416)(82) = 201,06 po².

ÉTAPE 2 : Trouvez l'aire du secteur AOB en pourcentage de l'aire totale.

A = 120/360 Aire du cercle, ou 0.333 X Aire du cercle.

En remplaçant 201,06 par l'aire du cercle (de l'ÉTAPE 1) :

A = (0,333) (201,06) = 66,95 po².

Segments

Une autre partie de la zone délimitée par un cercle est appelée segment. Un segment est délimité par un arc et un accord. Un accord est toute ligne droite passant par le cercle à deux points.

Un segment est une partie d'un secteur et, comme un secteur, il est mesuré par l'angle central.

La figure 10-39 illustre un segment d'un cercle. Il est délimité par l'arc du cercle et par accord AB.

Fig. 10-39. Un segment

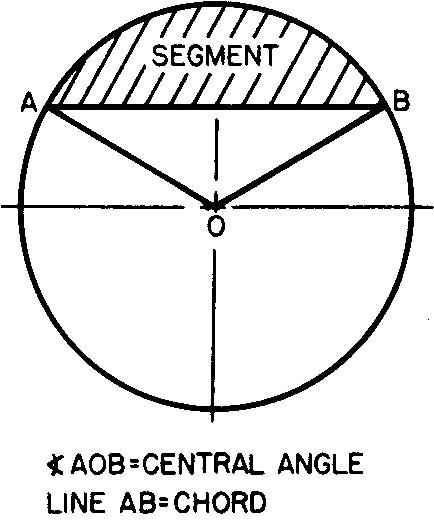
Exemple Trouver la zone des segments

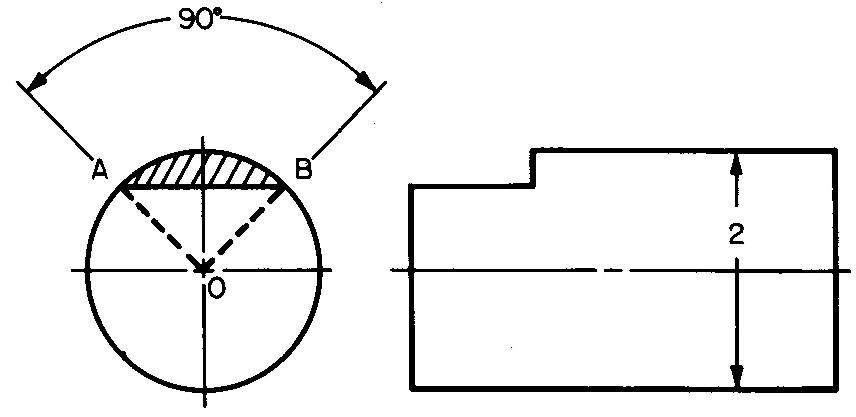
Calculez la zone du segment ombré de la partie machine qui est illustrée à la figure 10-40.

Fig. 10-40

Solution

Zone du segment = zone du secteur - zone du triangle AOB.

Étape 1: comme développé dans la Sec. 10.17, zone du secteur = à πr² (90/360).

La figure 10-40 donne l'angle central pour le secteur à 90 °.

Remplacer 3.1416 par π (Fig. 10-36) et 1 par R (calculé à partir de la figure 10-40. D = 2in., donc r = 1 po.):

A = (3,1416) (L2) (0,25) = 0,7854 sq. po.

Étape 2: De la figure 10-29, zone de triangle = 1/2 ab.

Remplacer 1 pour A et 1 pour B (Fig. 10-40 donne A et B comme 1 po. Les rayons du cercle):

A = 1/2 (1) (1) = 0,5 po.

Étape 3: zone du segment = zone du secteur - zone du triangle.

Remplacement de 0,7854 à la superficie du secteur (à partir de l'étape 1) et de 0,5 à la superficie du triangle (à partir de l'étape 2):

A = 0,7854 - 0,5. A = 0,2854 sq. po.

Prismes et cylindres

Des figures solides avec des bases congruentes et parallèles et des bords parallèles sont appelés prismes. Ils sont uniformes en section transversale.

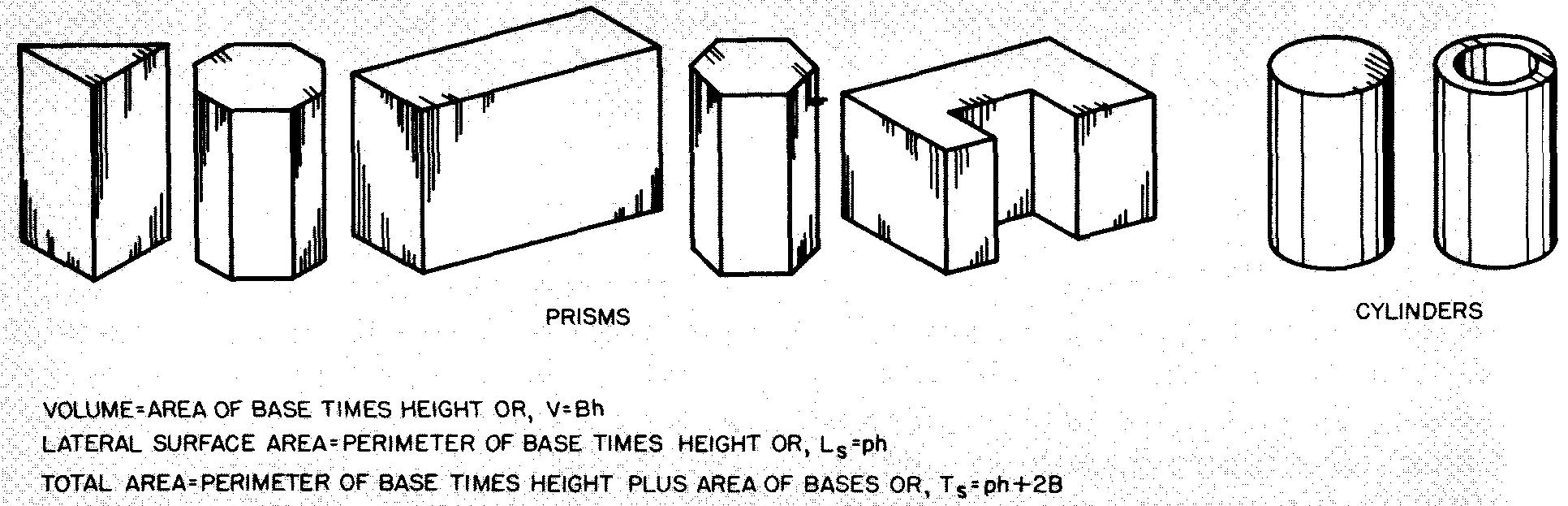
Comme le montre la figure 10-41, les cylindres peuvent être distingués des prismes par leurs bases circulaires.

Fig. 10-41. Prismes et cylindres

Exemple 1 Calcul de poids

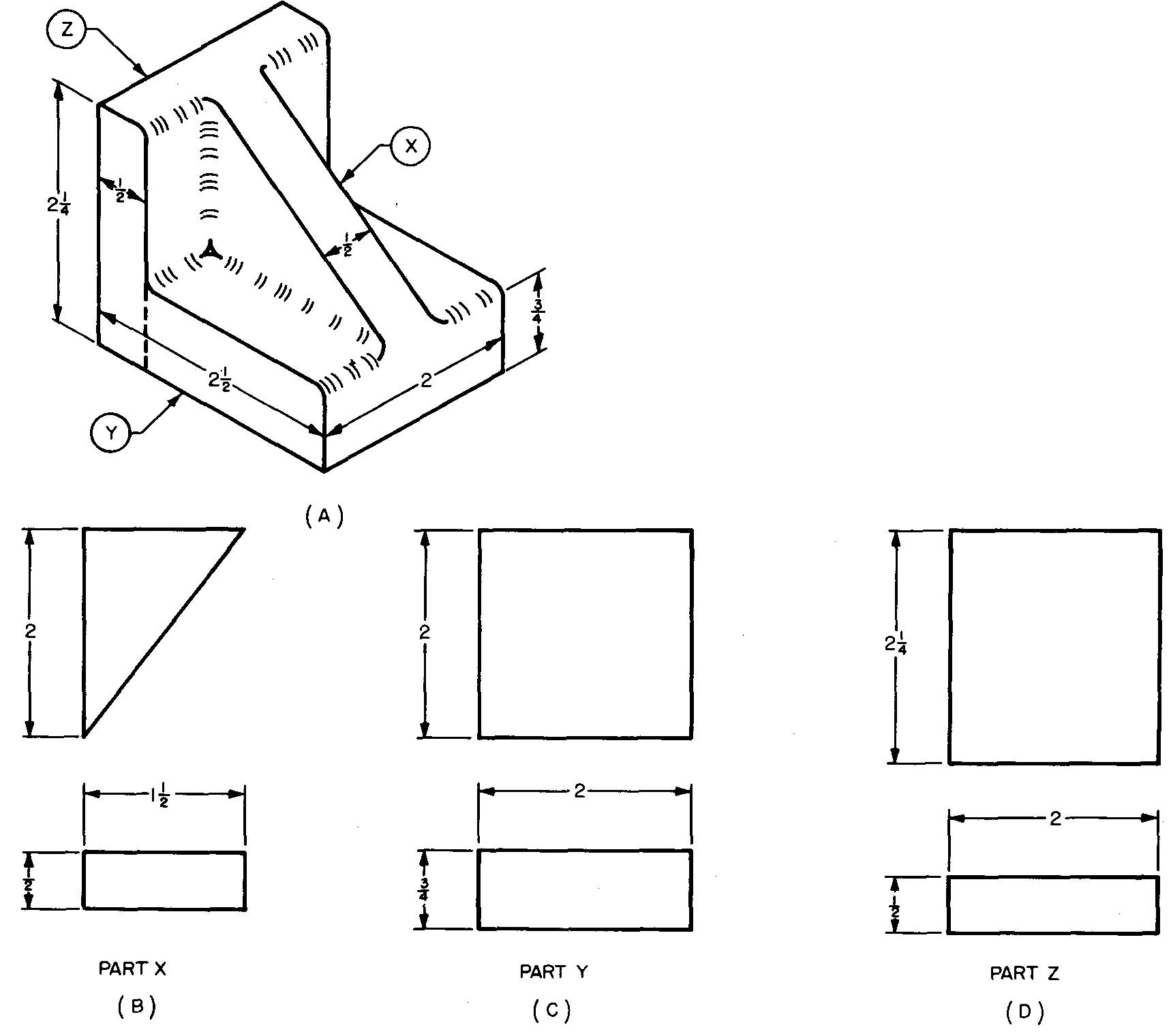
Calculez le poids de la coulée sur la figure 10-42A. Ignorer les filets et les rondes. La fonte pèse 0,26 livres par pouce cube.

Fig. 10-42

Solution

Pour plus de simplicité, divisez la coulée dans les trois parties indiquées séparément sur la figure 10-42b via D. Trouvez le volume de chaque partie. Ajoutez ensuite ces volumes pour trouver le volume total.

Enfin, multipliez le volume total par le poids par pouce cube pour trouver le poids total.

Étape 1: Pour trouver le volume de la partie x (Fig. 10-42B), utilisez la formule de la figure 10-41:

V = bh.

Pour trouver la zone de la base (b), utilisez la formule de la figure 10-29: A = 1/2 AB.

Substituant cela par b: v = (1/2 ab) h.

Remplacer 2 par A, 1,5 par B et 0,5 par H (donné sur la figure 10-42B):

V = (0,5) (2) (1,5) (0,5) = 0,75 cu. po.

Étape 2: Pour trouver le volume de la partie Y (Fig. 10-42C), utilisez la formule V = BH.

Pour trouver B, utilisez la formule de la figure 10-9: A = S².

Substituant cela par b: V = s²h.

Remplacer 2 par S et 0,75 par H (donné sur la figure 10-42C):

V = (22) (0,75) = 3 cu. po.

Étape 3: Pour trouver le volume de la partie Z (Fig. 10-42D), utilisez la formule V = BH.

Pour trouver B, utilisez la formule pour un rectangle: a = lw.

En substituant cela par b: v = iwh.

Remplacer 2 ppour I, 2,25 pour W et 0,5 pour H (donné sur la figure 10-42d):

V = (2) (2,25) (0,5) = 2,25 cu. po.

Étape 4: Pour trouver le volume total, ajoutez les volumes:

Vt = x + y + z.

Remplacer 0,75 par x (à partir de l'étape 1), 3 par Y (à partir de l'étape 2) et 2,25 par Z (à partir de l'étape 3):

Vt = 0,75 + 3 + 2,25 = 6 Cu. dans.

Étape 5: La fonte pèse 0,26 livres par pouce cube.

Le poids total (Wt) est égal à Vt X Poids par unité de volume (W).

Remplacer 6 par Vt et 0,26 par W:

Wt = (6) (0,26) = 1,56 lb.

Exemple 2 Calcul de Volume

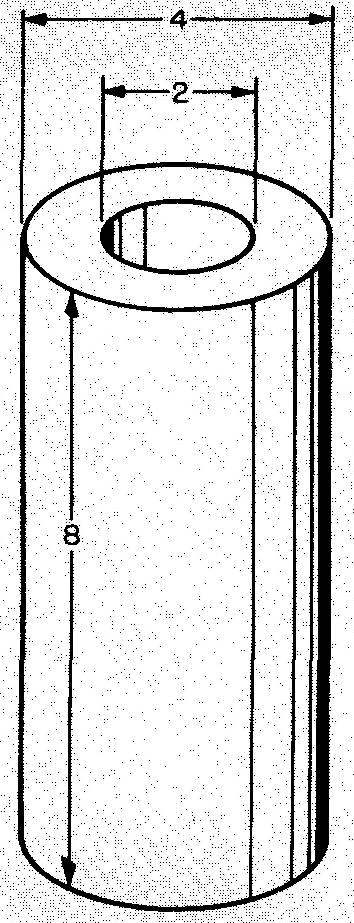
Calculez le volume du tuyau illustré à la Fig. 10-43.

Fig. 10-43

Solution

Trouvez le volume du cylindre entier.

Trouvez ensuite le volume du trou.

La différence entre ces deux valeurs correspondra au volume du tuyau.

ÉTAPE 1 : Pour trouver le volume du cylindre entier, utilisez la formule :

V = Bh

Pour trouver B, utilisez la formule de la Fig. 10-36 : A =πr².

En remplaçant B par ceci : V = (πr²) h.

En remplaçant π par 3,1416 (Fig. 10-36), r par 2 (calculé à partir de la Fig. 10-43. D = 4 po,

donc r = 2 po), et h par 8 (donné à la Fig. 10-43) :

V= (3,1416) (22) (8). V= 100,5312 pi³.

ÉTAPE 2 : Pour trouver le volume du trou, utilisez la même formule :

V = Bh, ou F= (πr²)h

En remplaçant π par 3,1416 (Fig. 10-36), r par 1 (calculé à partir de la Fig. 10-43.

D = 2 po, donc r= 1 po), et h par 8 (donné dans la Fig. 10-43) :

V= (3,1416)(12)(8) = 25,1328 po³

ÉTAPE 3 : Pour trouver le volume du tuyau, soustrayez le volume du trou du volume du cylindre.

À partir de l'ÉTAPE 1, le volume du cylindre = 100,5312 po³ et à partir de l'ÉTAPE 2, le volume du trou = 25,1328 po³.

V = 75,3984 po³.

Exemple 3 : calcul de la surface latérale et totale

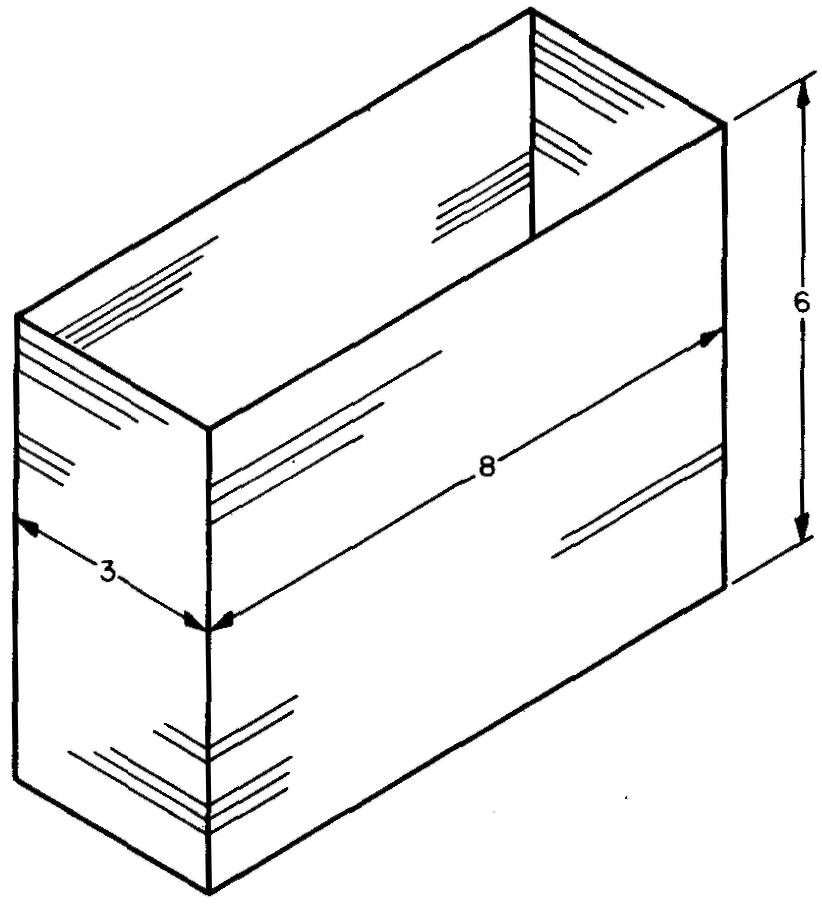
Calculez la surface latérale et extérieure totale du réservoir en tôle illustré à la Fig. 10-44. Le réservoir est ouvert en haut.

Fig. 10-44

Solution

ÉTAPE 1 : Comme illustré à la Fig. 10-41, Ls = ph. p = 2w + 21

En remplaçant p par ceci : L8= (2w + 2l)h.

En remplaçant 3 par w, 8 par l et 6 par h (donné à la Fig. 10-44) :

L= [(2)(3) + (2)(8)]6 = 132 po².

ÉTAPE 2 : Pour trouver la surface totale, utilisez la formule de la Fig. 10-41 : Ts = La + B.

N'oubliez pas que ce réservoir a une base.

Pour trouver B, utilisez la formule : A = Iw.

En remplaçant B par ceci : Ts = Ls + Iw.

En remplaçant Ls par 132 (de l'ÉTAPE 1), l par 8 et w par 3 (donné dans la Fig. 10-44) :

Ts= 132+ (8)(3) = 156 po².

Pyramides droites et cônes

Une pyramide est un solide, généralement doté d'une figure plane équilatérale pour base et de trois faces triangulaires équilatérales ou plus qui se rencontrent en un point appelé sommet.

Une pyramide droite est une pyramide dont le sommet se trouve sur la ligne perpendiculaire au centre de sa base. Une pyramide droite est représentée sur la figure 10-45A.

Fig. 10-45. Une pyramide et un cône

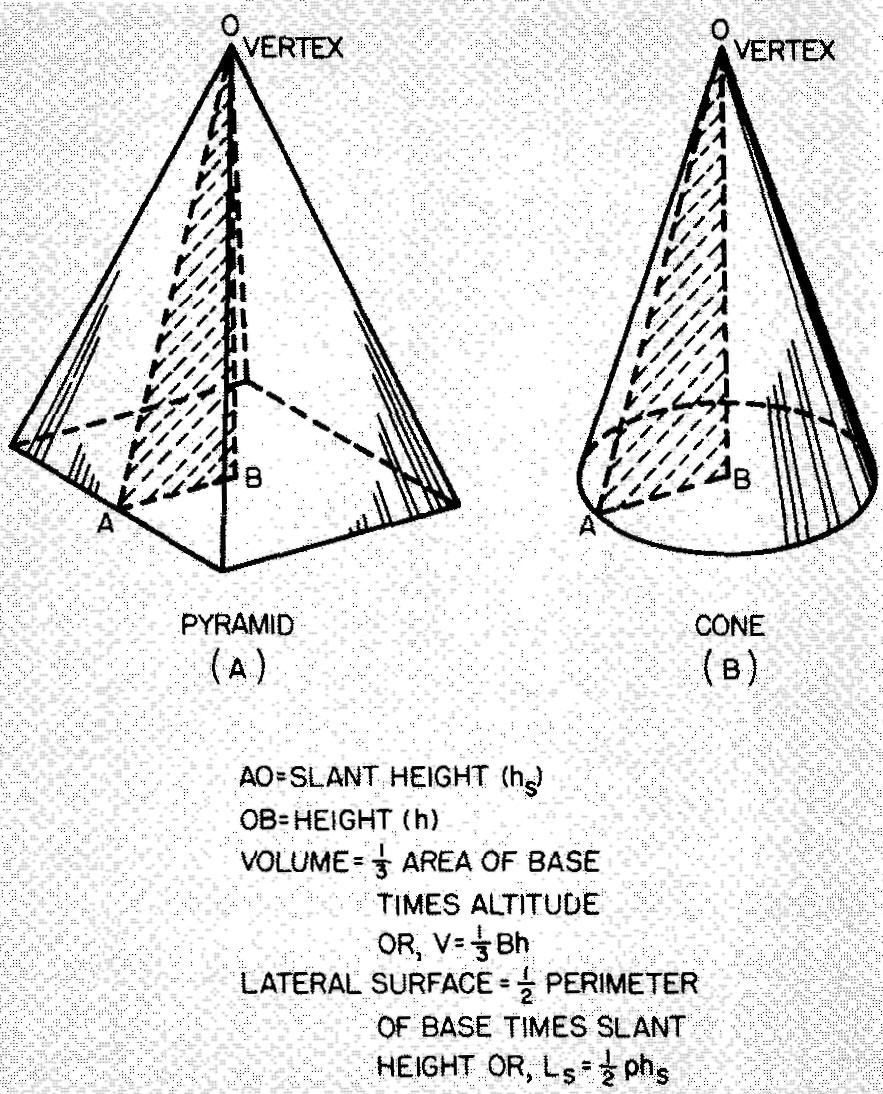
Un cône est une figure solide formée d'une surface latérale et d'une base unique délimitée par un cercle. Le sommet d'un cône droit se trouve sur une ligne perpendiculaire à la base au centre de la base. La figure 10-45B montre un cône droit.

Exemple 1 : calcul du volume et de l'aire latérale

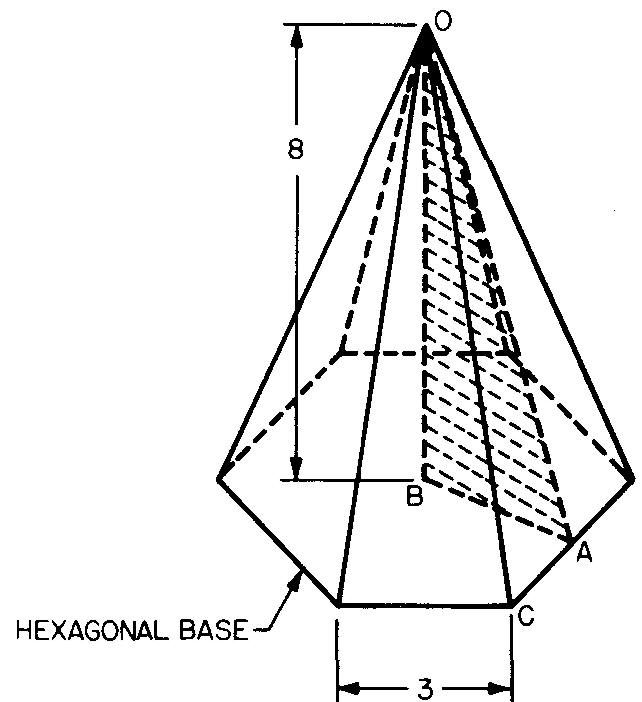
Calculez le volume et l'aire latérale de la pyramide représentée sur la figure 10-46.

Fig. 10-46

solution

ÉTAPE 1 : Comme indiqué dans la Fig. 10-45, V = 1/3 Bh.

Pour trouver B, utilisez la formule de la Fig. 10-12 : A = 2,598s²

En remplaçant B par ceci : V= 1/3 (2,598s²) h.

En remplaçant s par 3 et h par 8 (donné dans la Fig. 10-46) :

V = 1/3(2,598)(3²) (8) = 62,352 cu. in.

ÉTAPE 2 : Pour trouver l'aire latérale (Ls), utilisez la formule donnée dans la Fig. 10-45 : Ls = 1/2 phs.

La hauteur oblique (hs) peut être trouvée en trouvant la longueur de l'hypoténuse du triangle ombré A OB dans la Fig. 10-46.

Pour trouver hs, utilisez la formule : c =√(a2 + b2)

Soit la droite AB = a, BO = b et AO = c.

D'après les informations données dans les Fig. 10-46 et 10-12, a = 1/2 f. La Figure 10-12 donne f = 1,732s

En remplaçant s par 3 (donné dans la Fig. 10-46) :

f = (1,732)(3) = 5,196.

En remplaçant f dans a = 1/2 f :

a= (1/2)(5,196) = 2,598 po.

En remplaçant a par 2,598 et b par 8 (donné dans la Fig. 10-46) :

c = √(2,598² + 8) = 8,41 po.

ÉTAPE 3 : Pour trouver l'aire latérale (Ls), utilisez la formule : Ls = 1/2 phs.

Pour trouver p, multipliez s par le nombre de côtés.

D'après la Fig. 10-46, 5 = 3 po et il y a 6 côtés, donc p = 18.

En remplaçant p par 18 et hs par 8,41 (d'après l'ÉTAPE 2) :

Ls = (1/2) (18) (8,41) = 75,69 po².

Exemple 2 : calcul du volume et de l'aire latérale

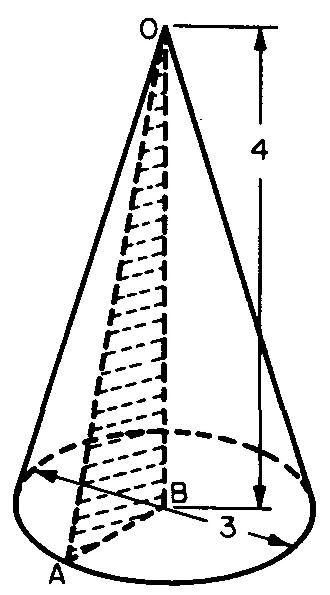
Calculez le volume et l'aire latérale du cône représenté sur la Fig. 10-47.

Fig. 10-47

Solution

ÉTAPE 1 : Pour trouver le volume, utilisez la formule de la Fig. 10-45 : V= 1/3 Bh.

Pour trouver B, utilisez la formule de la Fig. 10-36 : A = πr².

En remplaçant B par ceci : V = 1/3(πr²)h.

En remplaçant 3,1416 (Fig. 10-36), 1,5 par r (calculé à partir de la Fig. 10-47. D = 3 po, donc r= 1,5 po), et 4 par h (donné sur la Fig. 10-47) :

V= 1/3(3,1416) (1,5²) (4) = 9,4248 pi3.

ÉTAPE 2 : Pour trouver l'aire latérale (Ls), utilisez la formule Ls = 1/2 phs.

La hauteur oblique (hs) est l'hypoténuse du triangle ombré AOB dans la Fig. 10-47.

c = √(a² + b²)

En remplaçant a par 1,5 et b par 4 :

c = √(1,5² + 4²)

c = 4,27 po.

Pour trouver p, utilisez la formule de la Fig. 10-36, C = πD.

En remplaçant π par 3,1416 (Fig. 10-36) et D par 3 (donné dans la Fig. 10-47) :

C = (3,1416) (3) = 9,4248 po.

En remplaçant p par 9,4248 et h₈ par 4,27 :

L₈ = (9,4248) (4,27) / 2 = 20,1219 po.ca.

Conicités

Lorsqu'une pièce de machine se rétrécit, le dessinateur peut avoir besoin de calculer la quantité de cône par pouce. À d'autres moments, il peut avoir besoin de calculer la quantité de cône pour la longueur de la pièce.

Dans d'autres cas, le dessinateur peut connaître la quantité de cône et la mesure d'un diamètre et peut avoir besoin de calculer la mesure de l'autre diamètre.

Les exemples suivants illustrent les calculs nécessaires pour ces différentes situations.
Exemple 1 Calcul de la quantité de cône

La conicité par pouce sur une pièce est de 0,05 pouce. Quelle est la conicité en 8 pouces ?
Solution

La conicité est de 0,05 pouce pour chaque pouce. Ainsi, la conicité en 8 pouces est de 8 fois 0,05 pouce.

Conicité = (8) (0,05), ou 0,4 po.

Exemple 2 Calcul de la quantité de cône

Quelle est la conicité par pouce si la conicité par pied est de 5/8 pouce ?

Solution

La conicité est de 5/8 pouce pour chaque pied. Ainsi, la conicité par pouce est de 1/12 de 5/8 pouce.

Conicité par pouce = 0,625 / 12, ou 0,052 po.

Exemple 3 calcul de la quantité de conicité

Calculez la conicité par pied pour la Fig. 10-48.

Fig. 10-48

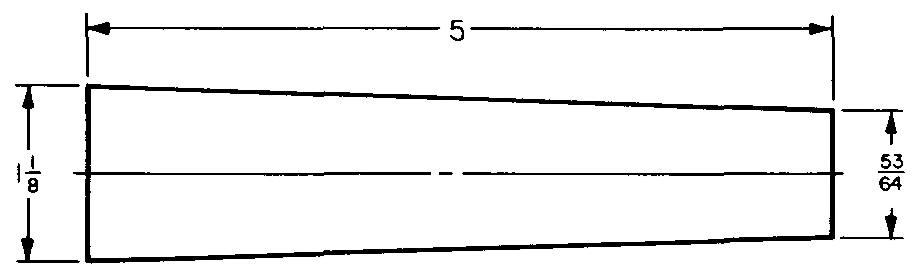
Solution

Conicité de la pièce = D - d.

En remplaçant 1,125 par D et 0,828125 par d (donné dans la Fig. 10-48) :

Conicité de la pièce = 1,125 - 0,828125.

Conicité de la pièce = 0,296875.

Conicité par pouce = Conicité divisée par la longueur.

En remplaçant 0,296875 par la conicité de la pièce et 5 par la longueur de la pièce (données dans la Fig. 10-48) :

Conicité par pouce = 0,296875 / 5.

Conicité par pouce = 0,059357 po.

Conicité par pied = 12 X Conicité par pouce.

Conicité par pied = (12) (0,059357), soit 0,7125 po.

Exemple 4 : calcul du diamètre

Calculez le petit diamètre de la Fig. 10-49. La conicité est de 0,6 pouce par pied.

Fig. 10-49.

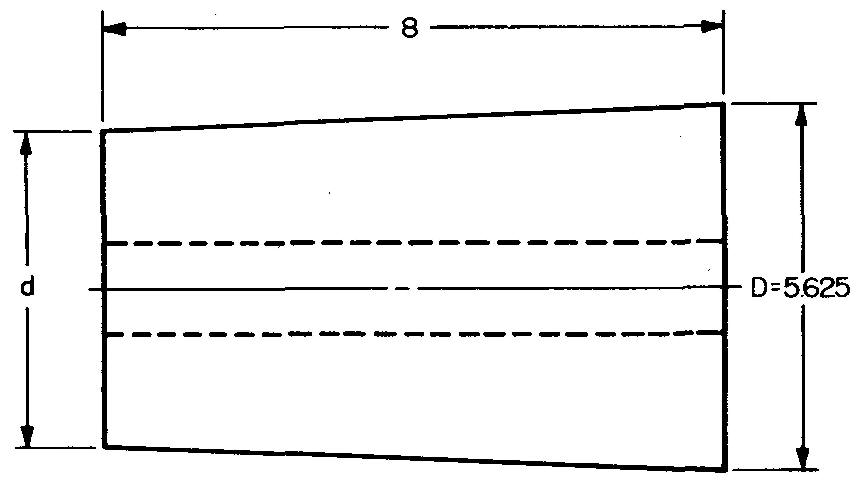
Solution

Conicité par pouce = Conicité par pied divisée par 12.

Conicité par pouce = 0,6/12, ou 0,05 po.

Conicité en 8 pouces = (8) (0,05), ou 0,4 po.

d = D - Conicité

En remplaçant 5,625 (donné dans la Fig. 10-49) par D et 0,4 par Conicité :

d = 5,625 - 0,4 = 5,225 po.

Exemple 5 : calcul du diamètre

Calculez le grand diamètre de la Fig. 10-50. La conicité est de 1/16 pouce par pouce.

Fig. 10-50

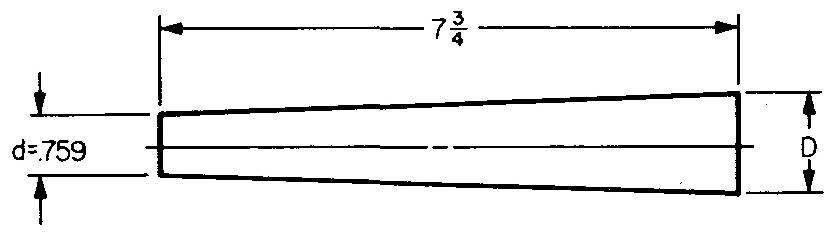
Solution

Conicité = Conicité par pouce multipliée par la longueur de la pièce.

Conicité = 0,0625 X 7,75, ou 0,484275 po. D = d + Conicité.

En remplaçant d par 0,759 (donné dans la Fig. 10-50) et par 0,484275 pour Taper : D = 0,759 + 0,484275, soit 1,243275 po.

Problèmes : révision des mathématiques de dessin (Les réponses ne sont pas données)

Ces problèmes de révision de cette section illustrent certains des types de problèmes mathématiques les plus courants et les plus courants qu'un dessinateur de machines devrait être capable de résoudre.

Pour chaque problème, déterminez les réponses pour les dimensions manquantes qui sont représentées par des lettres.

N'oubliez pas qu'un croquis à main levée sera souvent d'une grande aide pour mettre en place le problème et pour trouver la solution au problème.

Certains des problèmes concernent des filetages de vis.

Certains symboles et termes répertoriés dans ces problèmes peuvent ne pas être clairement compris. Il est suggéré qu'avant de commencer ces problèmes, l'étudiant se réfère à la section 12 (Opérations d'usinage de base) pour ces informations

problème 10-1	problème 10-2
problème 10-3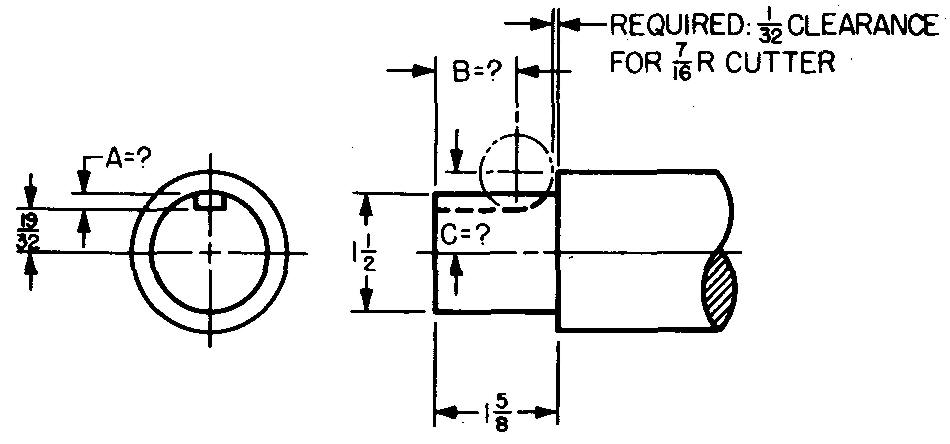	problème 10-4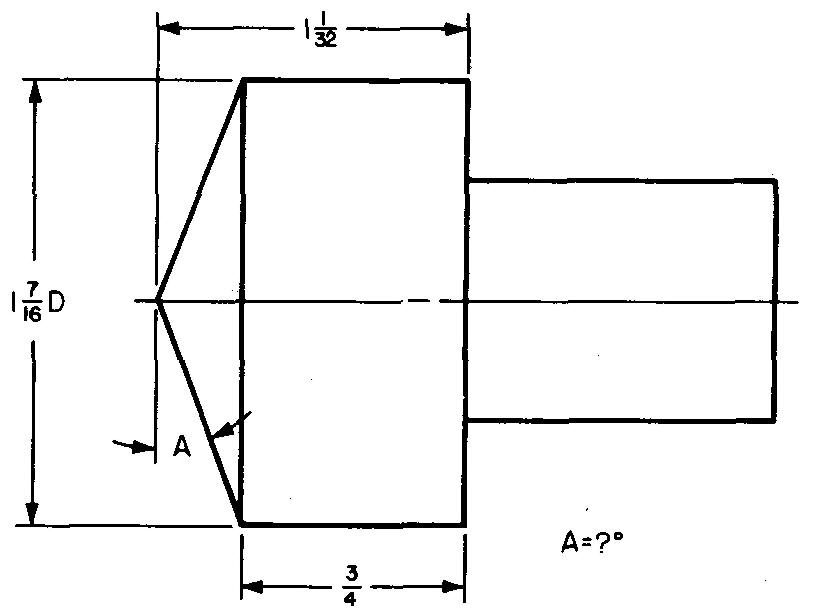
problème 10-5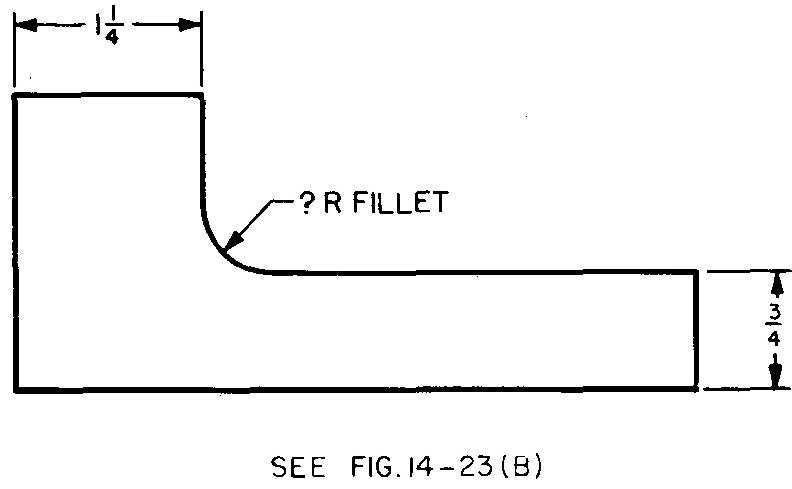	problème 10-6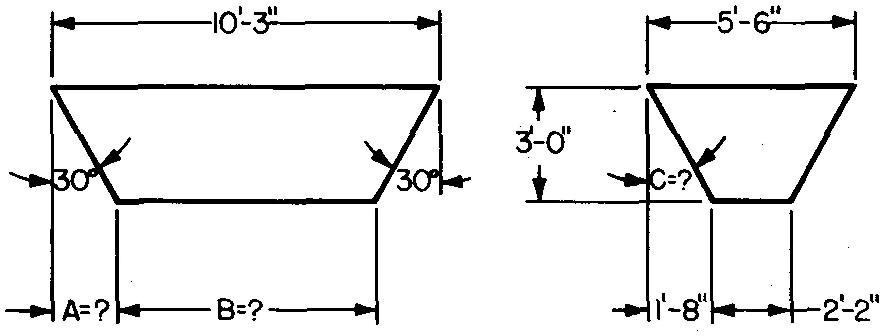
problème 10-7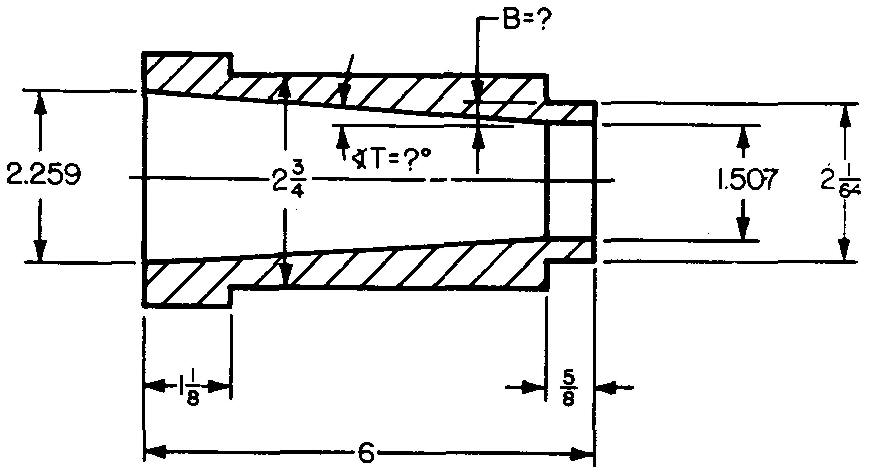	problème 10-8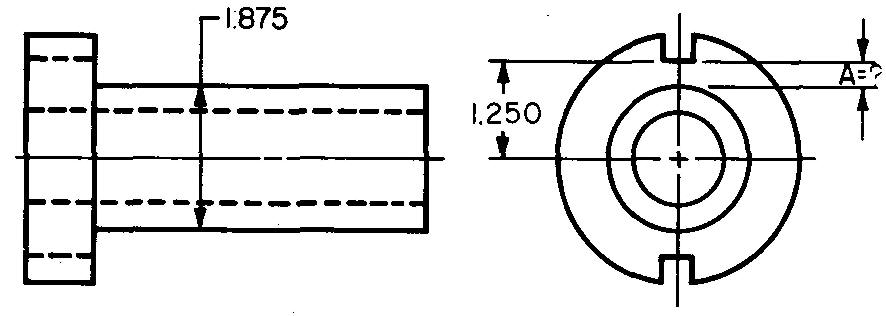
problème 10-9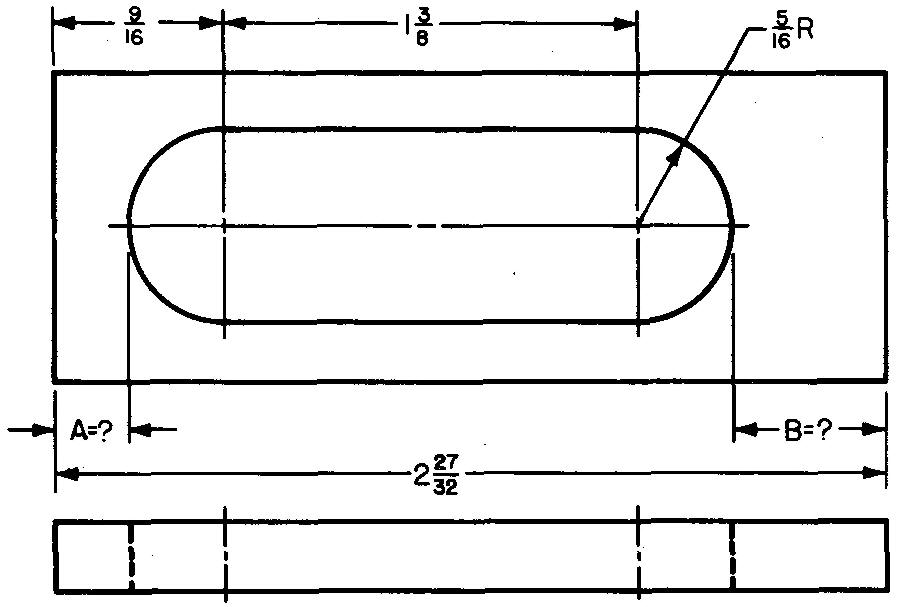	problème 10-10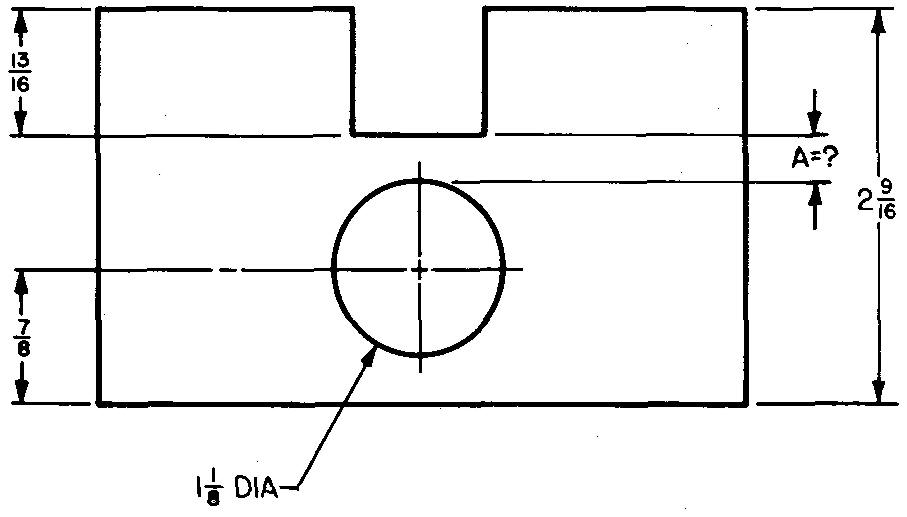
problème 10-11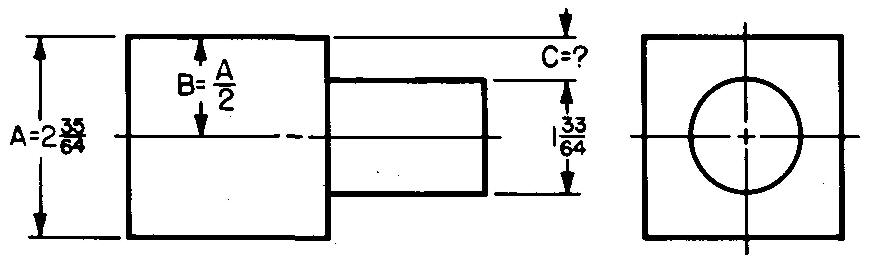	problème 10-12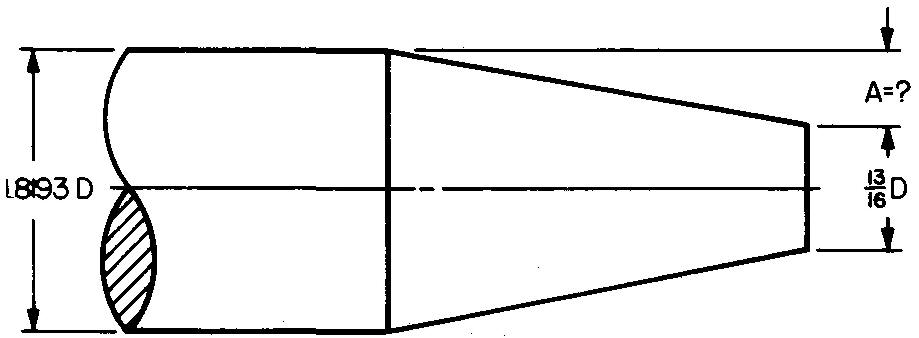
problème 10-13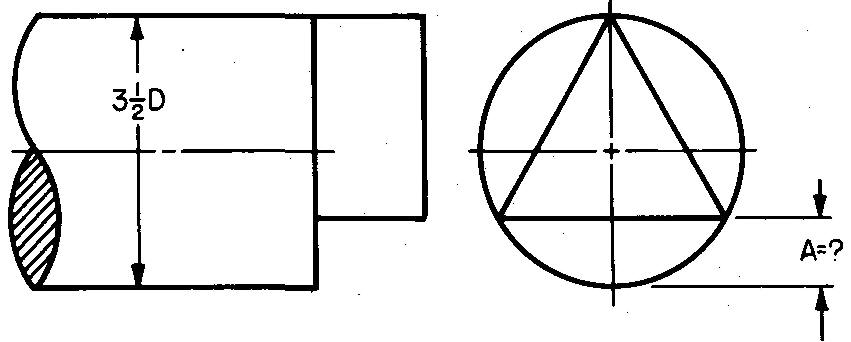	problème 10-14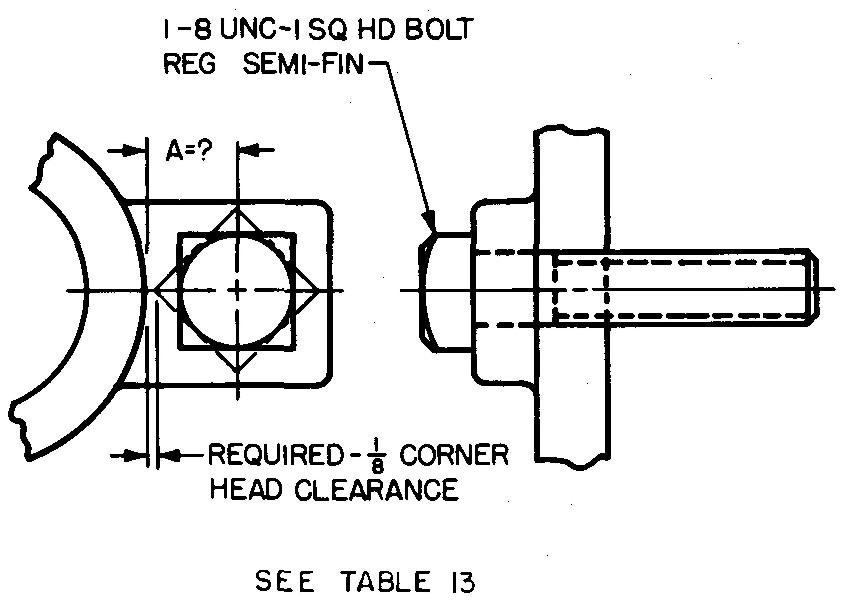
problème 10-15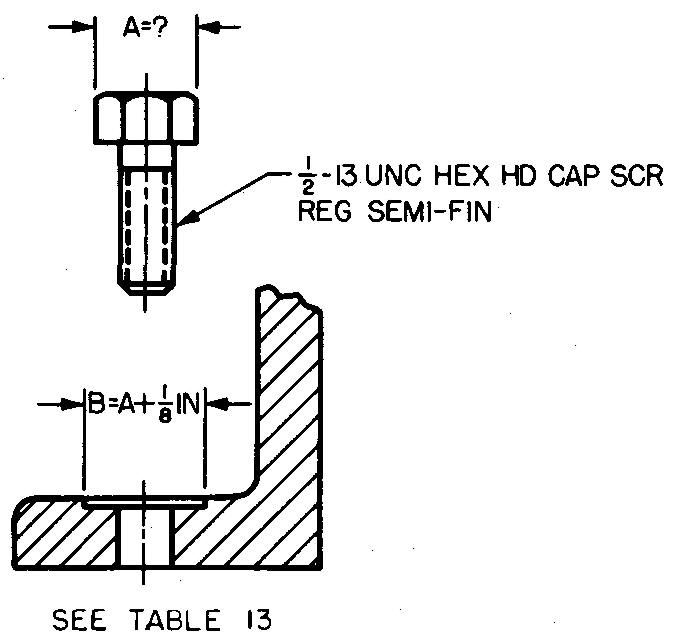	problème 10-16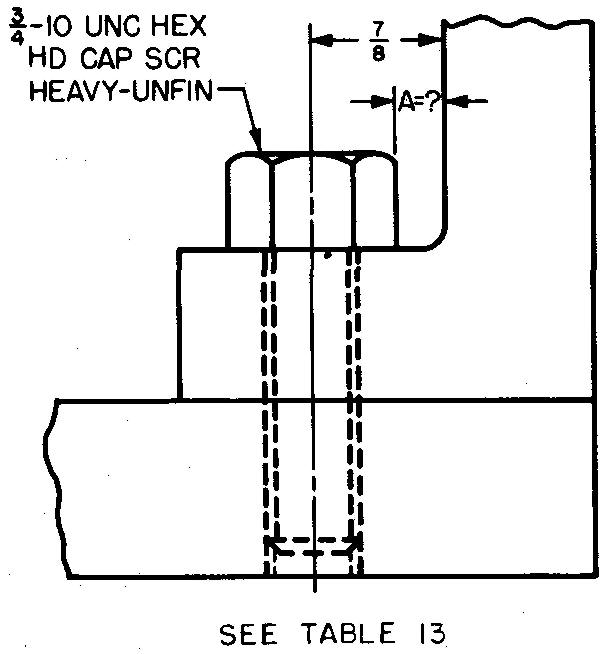
problème 10-17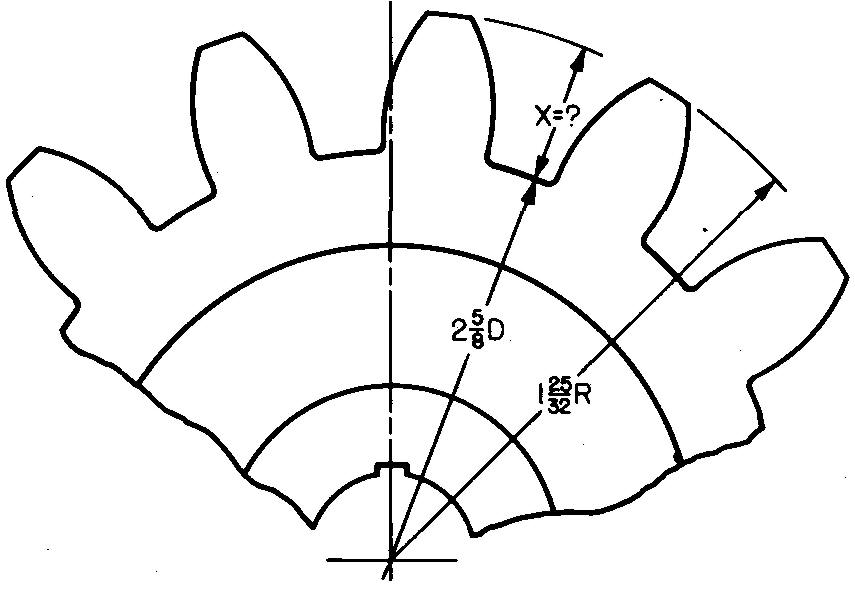	problème 10-18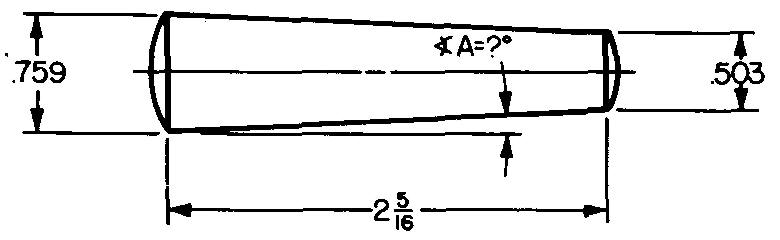
problème 10-19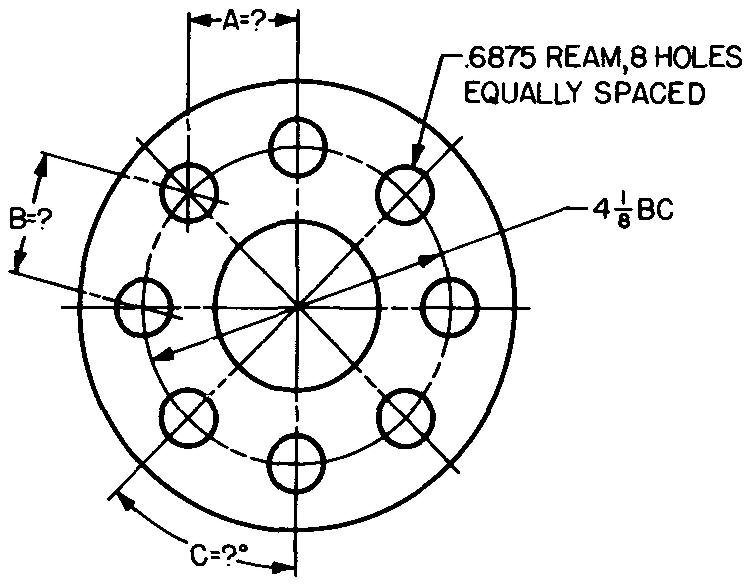	problème 10-20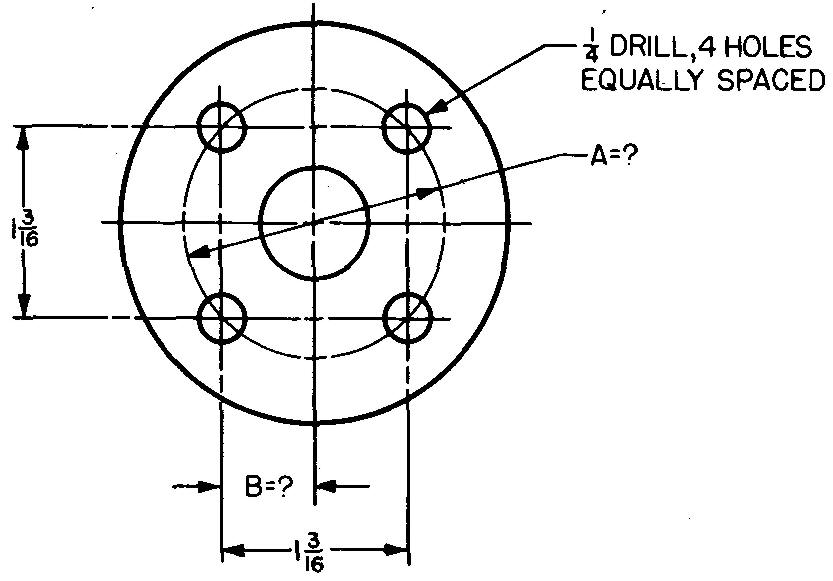
problème 10-21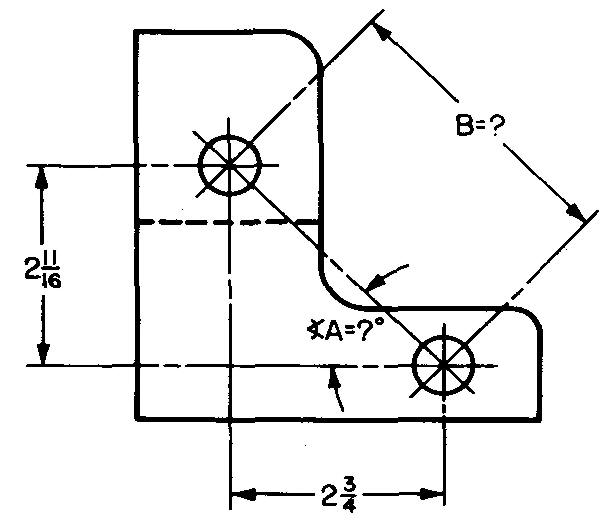	problème 10-22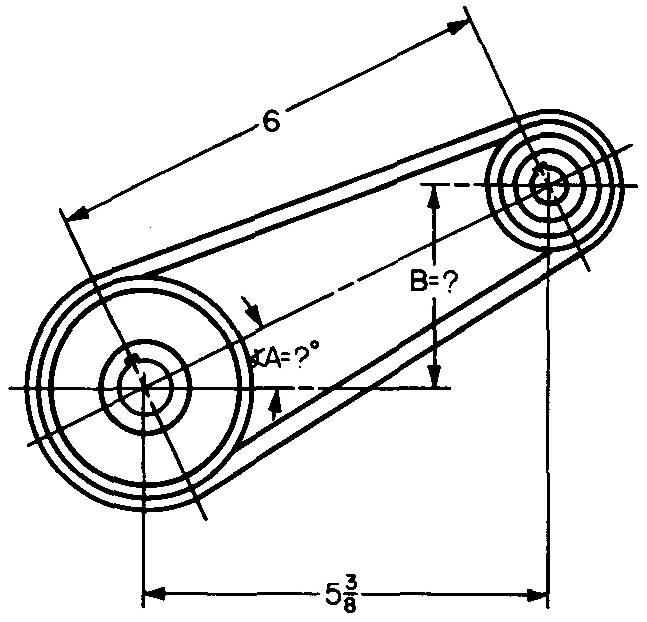
problème 10-23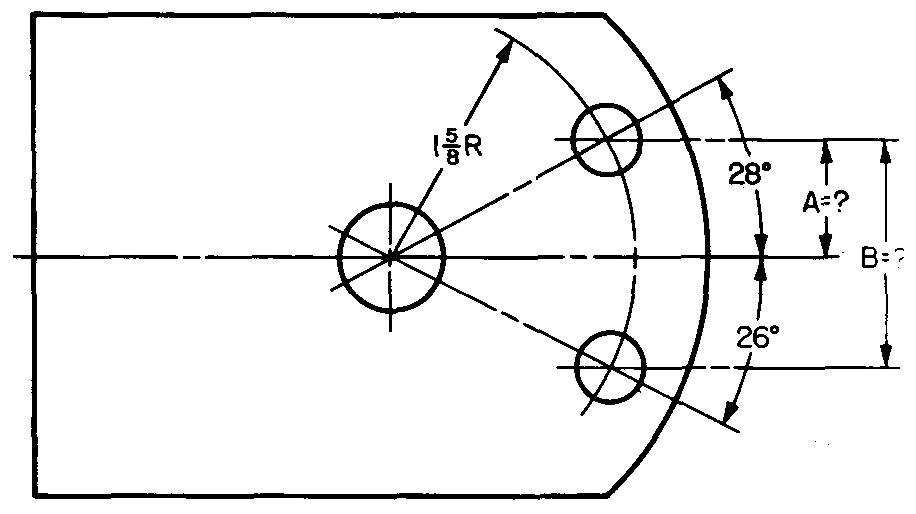	problème 10-24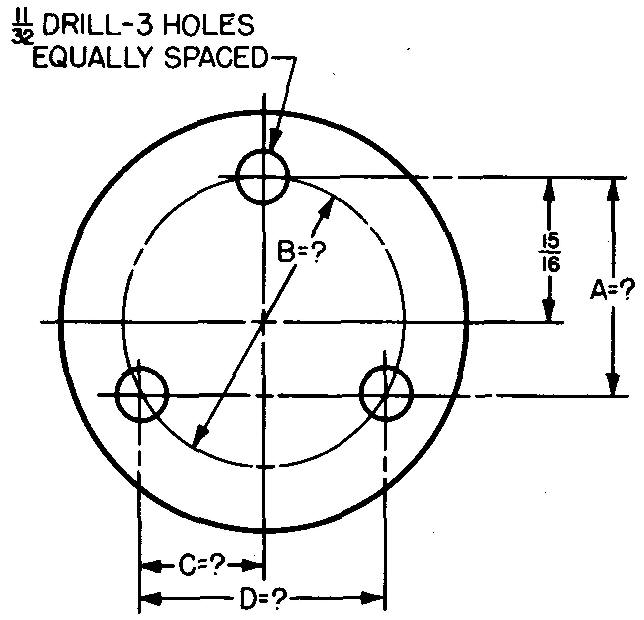
problème 10-25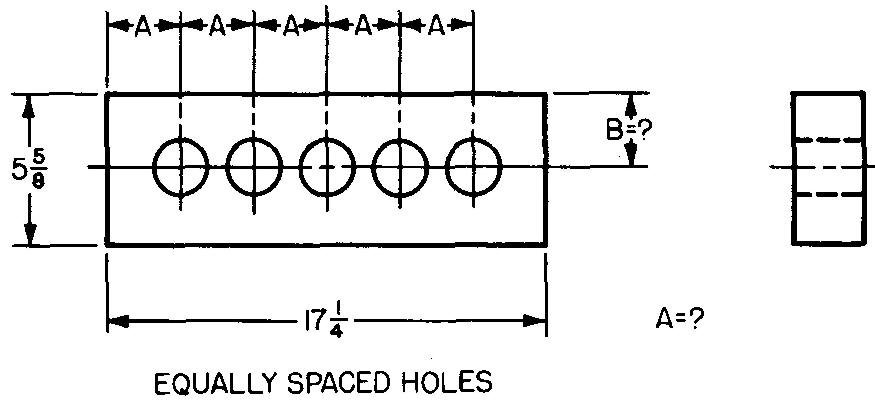	problème 10-26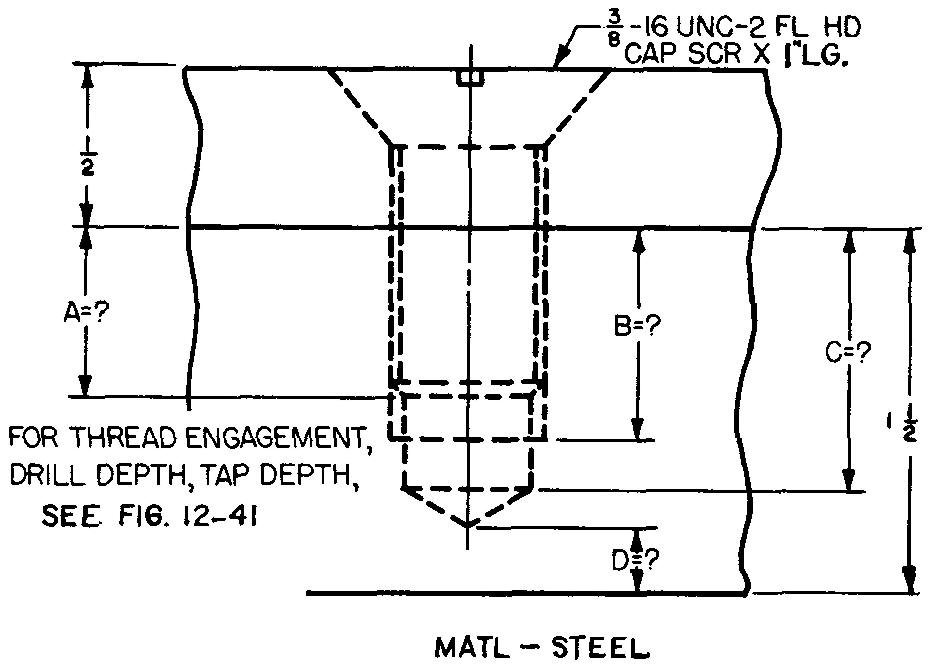
problème 10-27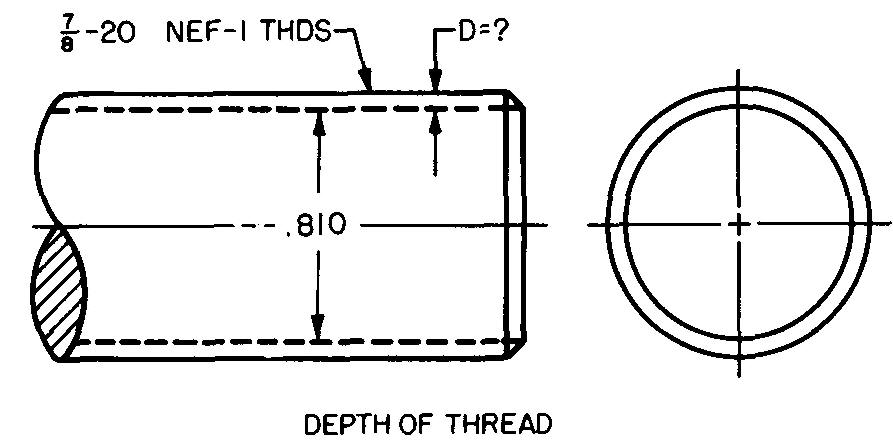	problème 10-28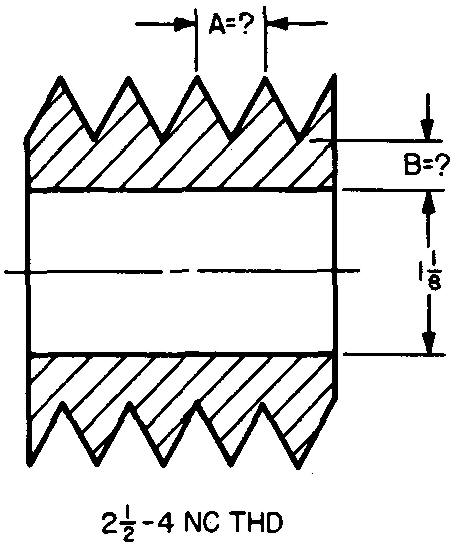
problème 10-29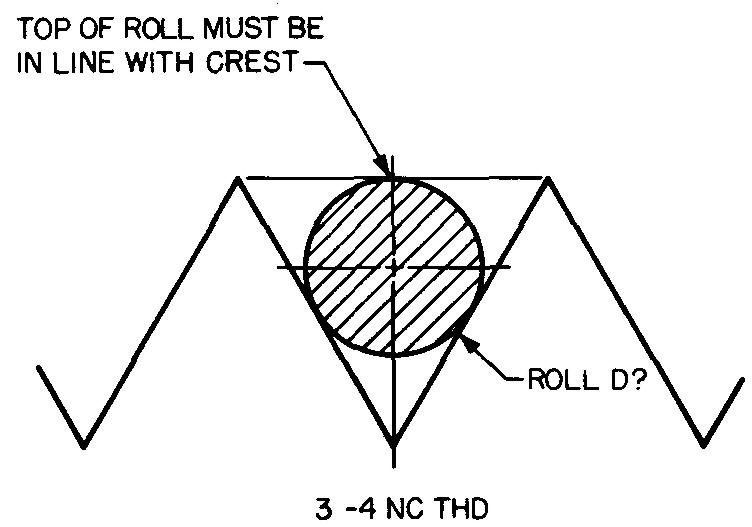	problème 10-30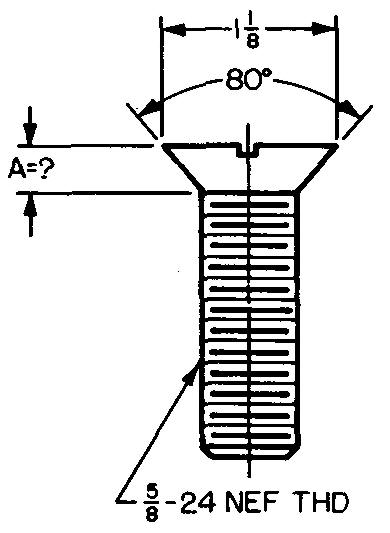
problème 10-31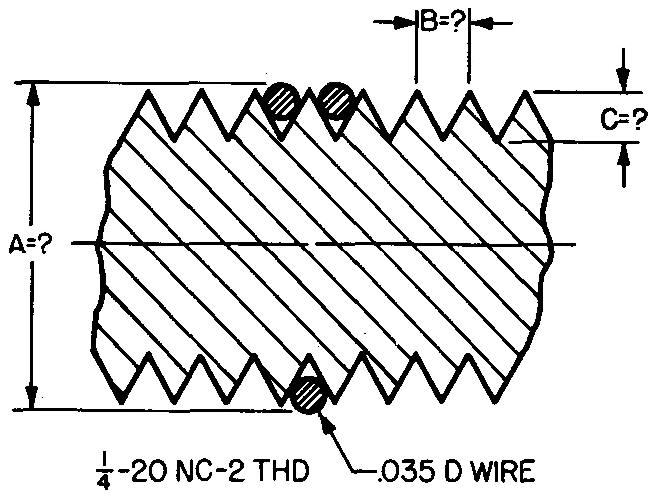	problème 10-32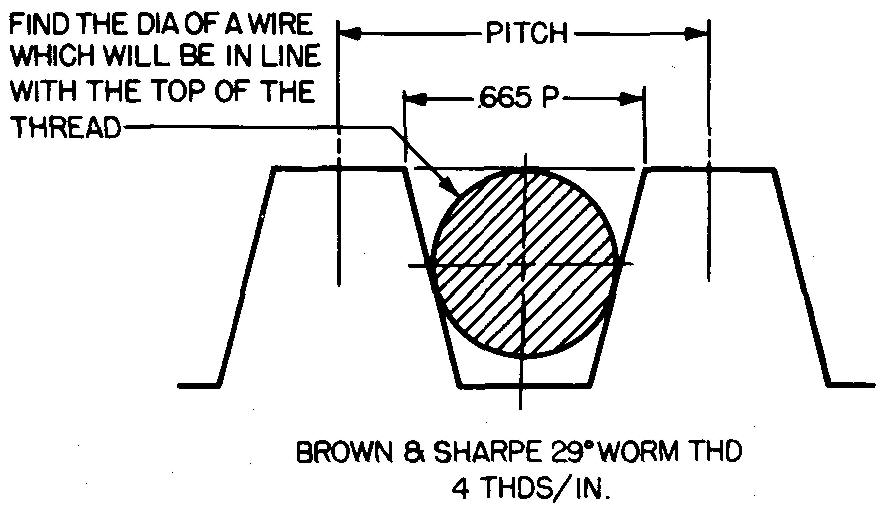
problème 10-33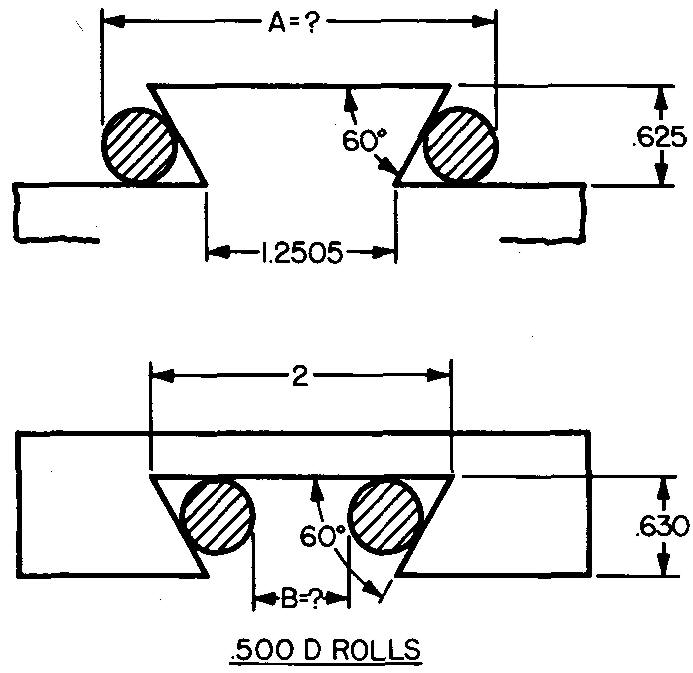	problème 10-34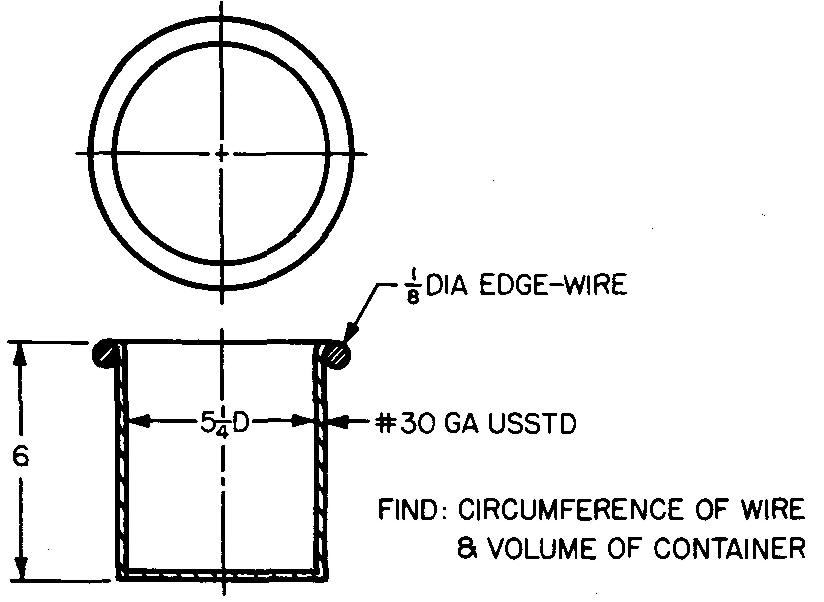
problème 10-35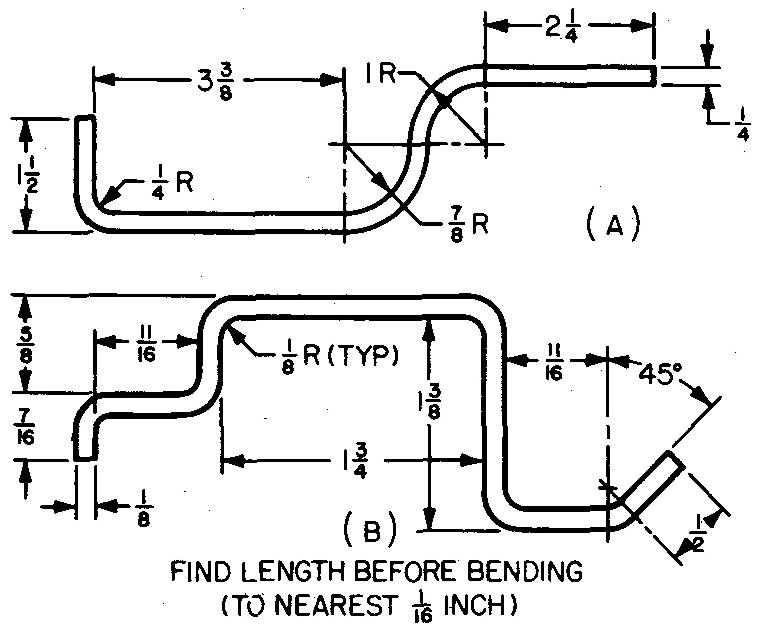	problème 10-36