Drafting mathematics Part 2
Circles
A circle is the set of all points on a plane equidistant from a point called the center of the circle. The center of the circle lies in the surface bounded by the circle.
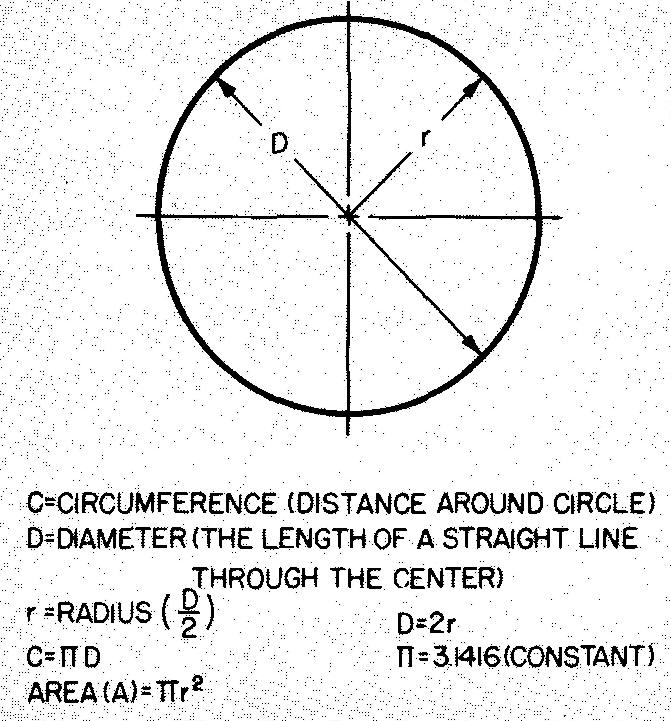
Figure 10-36 gives the formulas for circles.
Fig. 10-36. A circle

Example 1 finding the circumference of a pulley
Calculate the circumference of a pulley with a diameter of 11-1/4 inches.
Solution
As shown in Fig. 10-36, C = πD
Substituting 3.1416 for π (given in Fig. 10-36) and 11.25 for D:
C=(3.1416)(11.25) = 35.343 in
Example 2 finding the area enclosed by a circle
Calculate the area of one end of a cylindrical tank with a diameter of 14 inches.
Solution
As shown in Fig. 10-36,
A = πr²
Substituting 3.1416 for π (given in Fig. 10-36) and 7 for r
calculated by dividing D by 2; D = 14 in., so r = 7 in:
A = (3.1416) (72) = 153.9384 sq. in.
Arcs and sectors
Figure 10-37 illustrates an arc and a sector of a circle. A sector is a portion of the area of a circle bounded by an arc and by two radii.
Fig. 10-37. An arc and a sector
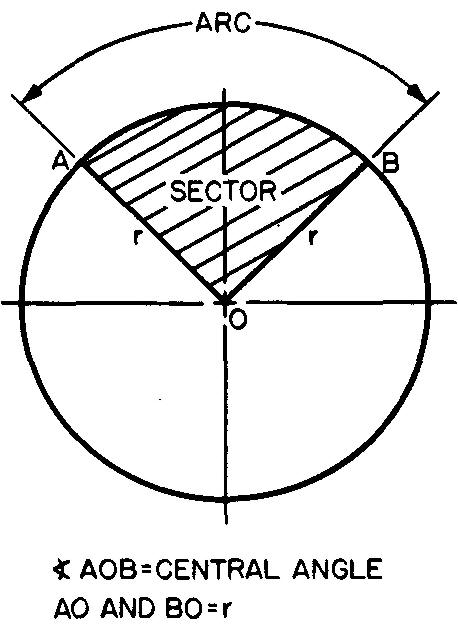
A sector may be thought of as a slice of pie. It is measured by the central angle, or the angle formed by the straight sides of the slice of pie. An arc is any portion of a circle. An arc is measured by its central angle.
Example 1 calculating the length of an arc
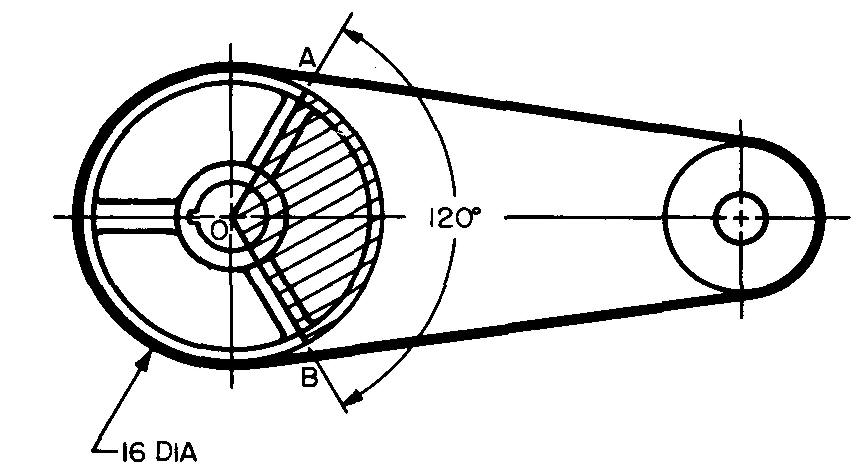
Calculate the length of arc AB of the shaded portion of the large pulley shown in Fig. 10-38.
Fig. 10-38
Solution
STEP 1:
To find the circumference of the whole circle, use C = πD from Fig. 10-36.
Substituting 3.1416 for π (given in Fig. 10-36) and 16 for D (given in Fig. 10-38):
C = (3.1416) (16) = 50.2656 in.
STEP 2:
Find the length of arc AB as a percent of the whole circumference. Figure 10-38 gives a measurement of 120° for arc AB.
Therefore arc AB — 120/360 of the whole circumference, or 0.333 times the circumference of the circle.
AB = 120/360 C
Substituting 50.2656 for C (from STEP 1):
AB = (0.333)(50.2656) = 16.738 in.
Example 2 finding the area of sectors
Calculate the area of the shaded sector ABO in Fig. 10-38.
Solution
STEP 1: To find the area of the whole circle, use A — Tir2 from Fig. 10-36.
Substituting 3.1416 for π (given in Fig. 10-36) and 8 for r (calculated from Fig. 10-38. D = 16 in., so r = 8 in.):
A = (3.1416)(82) = 201.06 sq. in.
STEP 2: Find the area of sector AOB as a percent of the whole area.
A = 120/360 Area of Circle, or 0.333 X Area of Circle.
Substituting 201.06 for Area of Circle (from STEP 1):
A = (0.333) (201.06) = 66.95 sq. in.
Segments
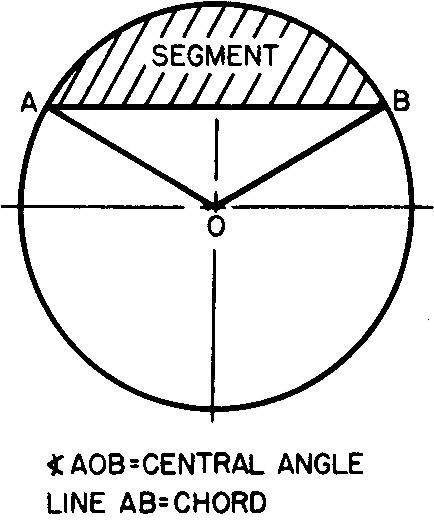
Another portion of the area bounded by a circle is called a segment. A segment is bounded by an arc and a chord. A chord is any straight line passing through the circle at two points.
A segment is a portion of a sector and, like a sector, it is measured by the central angle.
Figure 10-39 illustrates a segment of a circle. It is bounded by the arc of the circle and by chord AB.
Fig. 10-39. A segment
Example finding the area of segments
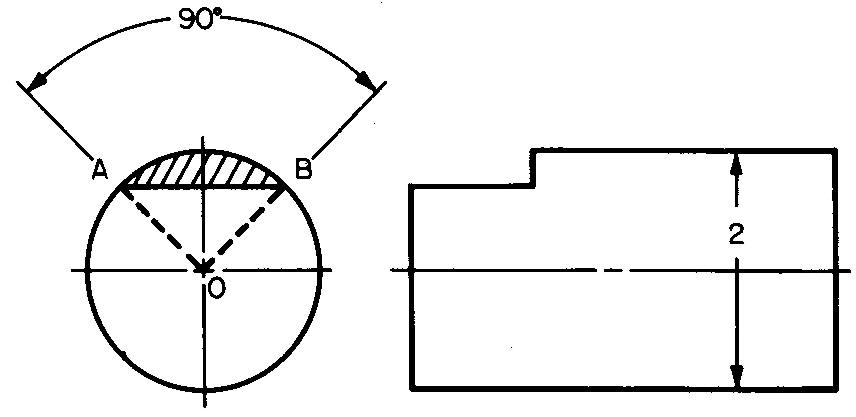
Calculate the area of the shaded segment of the machine part that is shown in Fig. 10-40.
Fig. 10-40
Solution
Area of Segment = Area of Sector - Area of Triangle AOB.
STEP 1: As developed in Sec. 10.17, Area of Sector = πr² (90/360).
Figure 10-40 gives the central angle for the sector as 90°.
Substituting 3.1416 for π (Fig. 10-36) and 1 for r (calculated from Fig. 10-40. D = 2in., so r = 1 in.):
A = (3.1416)(l2)(0.25) = 0.7854 sq. in.
STEP 2: From Fig. 10-29, Area of Triangle = 1/2 ab.
Substituting 1 for a and 1 for b (Fig. 10-40 gives a and b as 1 in. radii of the circle):
A = 1/2(1)(1) = 0.5 sq. in.
STEP 3: Area of Segment = Area of Sector - Area of Triangle.
Substituting 0.7854 for Area of Sector (from STEP 1) and 0.5 for Area of Triangle (from STEP 2):
A = 0.7854 - 0.5. A = 0.2854 sq. in.
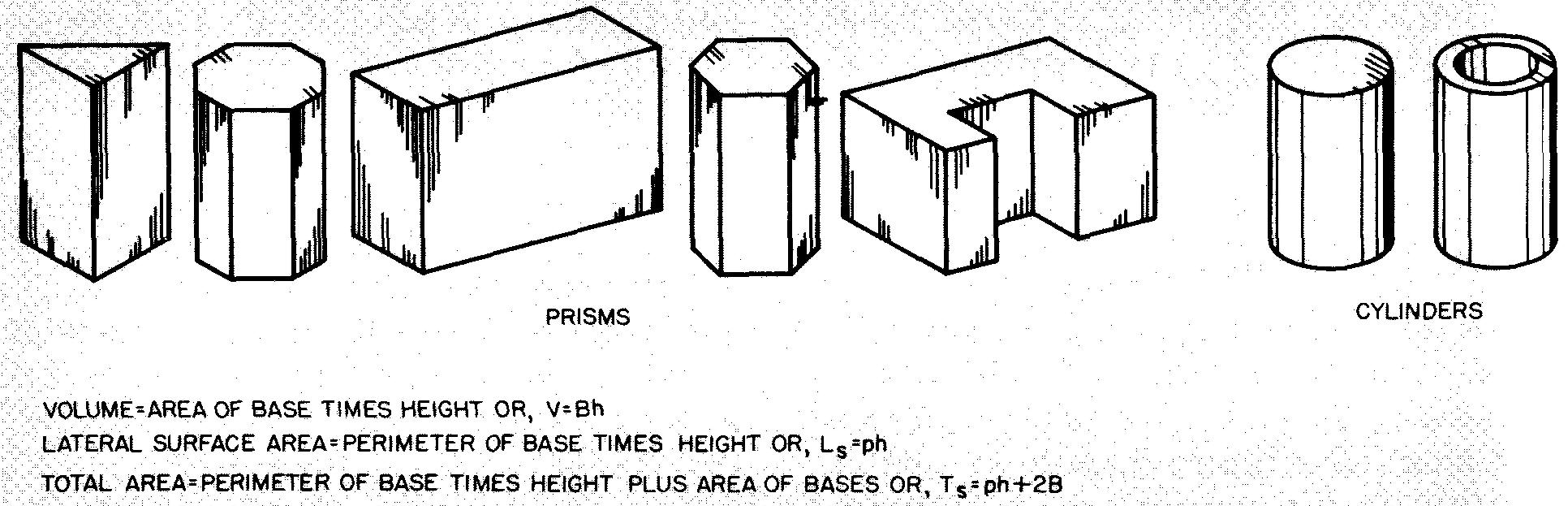
Prisms and cylinders
Solid figures with congruent and parallel bases and parallel edges are called prisms. They are uniform in cross section.
As shown in Fig. 10-41, cylinders can be distinguished from prisms by their circular bases.
Fig. 10-41. Prisms and cylinders
Example 1 calculating weight
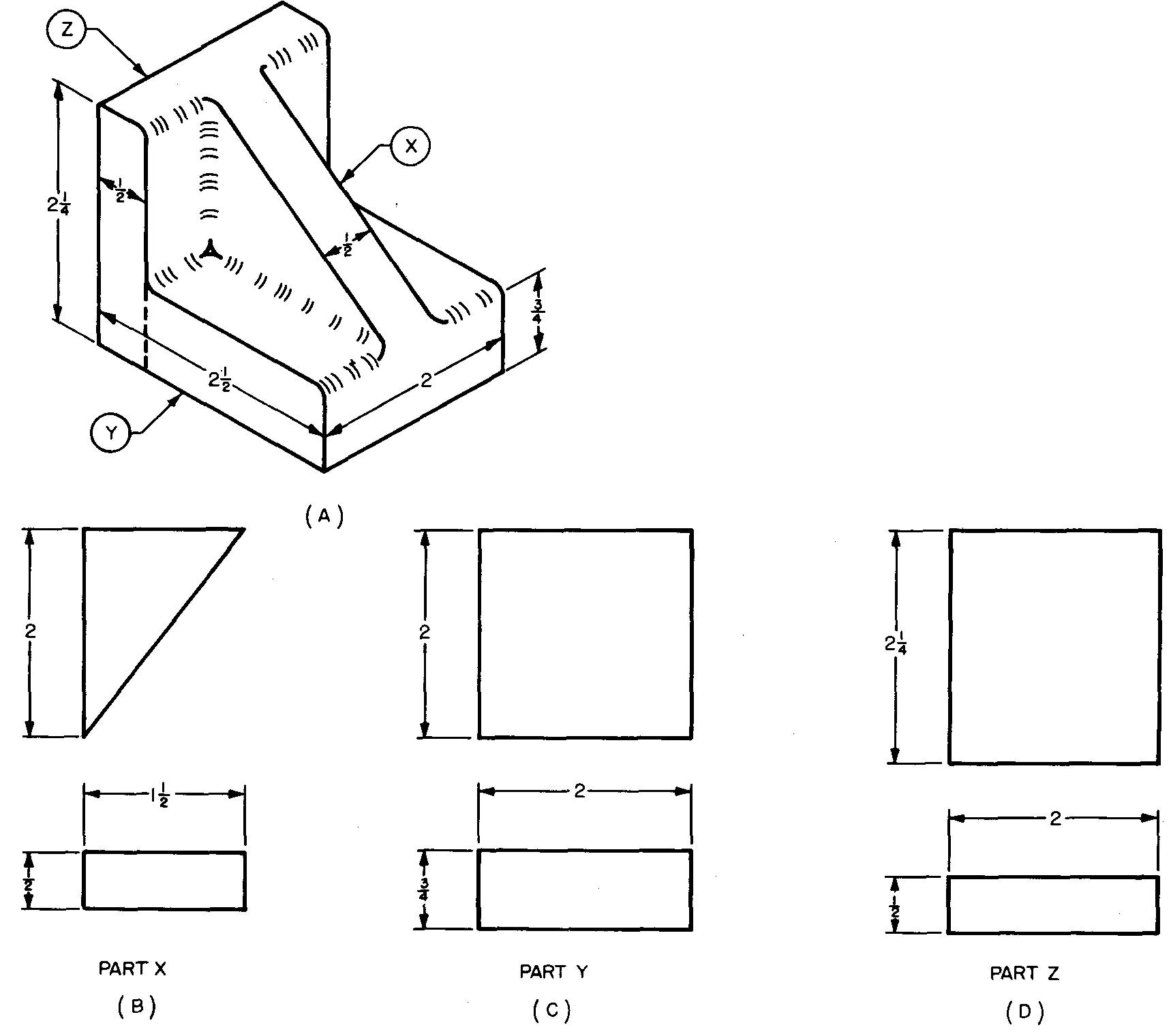
Calculate the weight of the casting in Fig. 10-42A. Disregard the fillets and rounds. Cast iron weighs 0.26 pounds per cubic inch.
Fig. 10-42
Solution
For simplicity, divide the casting into the three parts shown separately in Fig. 10-42B through D. Find the volume of each part.
Then add these volumes together to find the total volume.
Finally, multiply the total volume by the weight per cubic inch to find the total weight.
STEP 1: To find the volume of part x (Fig. 10-42B), use the formula from Fig. 10-41:
V = Bh.
To find the area of the base (B), use the formula from Fig. 10-29: A = 1/2 ab.
Substituting this for B: V = (1 /2 ab) h.
Substituting 2 for a, 1.5 for b, and 0.5 for h (given in Fig. 10-42B):
V= (0.5) (2) (1.5) (0.5) = 0.75 cu. in.
STEP 2: To find the volume of part y (Fig. 10-42C), use the formula V = Bh.
To find B, use the formula from Fig. 10-9: A=s².
Substituting this for B: V = s²h.
Substituting 2 for s and 0.75 for h (given in Fig. 10-42C):
V= (22) (0.75) = 3 cu. in.
STEP 3: To find the volume of part z (Fig. 10-42D), use the formula V = Bh.
To find B, use the formula for a rectangle: A =lw.
Substituting this for B: V = Iwh.
Substituting 2 for I, 2.25 for w, and 0.5 for h (given in Fig. 10-42D):
V= (2) (2.25) (0.5) = 2.25 cu. in.
STEP 4: To find the total volume, add the volumes:
Vt = x + y + z.
Substituting 0.75 for x (from STEP 1), 3 for y (from STEP 2), and 2.25 for z (from STEP 3):
Vt = 0.75 + 3 + 2.25 = 6 cu. in.
STEP 5: Cast iron weighs 0.26 pounds per cubic inch.
Total weight (Wt) equals Vt X weight per unit volume (w).
Substituting 6 for Vt and 0.26 for w:
WT= (6) (0.26) = 1.56 lb.
Example 2 calculating volume
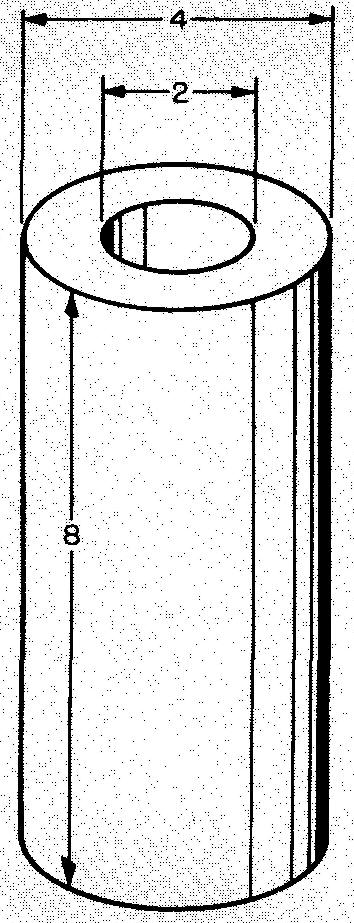
Calculate the volume of the pipe shown in Fig. 10-43.
Fig. 10-43
solution
Find the volume of the entire cylinder.
Then find the volume of the hole.
The difference between these will be the volume of the pipe.
STEP 1: To find the volume of the entire cylinder, use the formula:
V = Bh
To find B, use the formula from Fig. 10-36: A =πr².
Substituting this for B: V = (πr²) h.
Substituting 3.1416 for π (Fig. 10-36), 2 for r (calculated from Fig. 10-43. D = 4 in.,
so r = 2 in.), and 8 for h (given in Fig. 10-43):
V= (3.1416) (22) (8). V= 100.5312 cu. in.
STEP 2: To find the volume of the hole, use the same formula:
V = Bh, or F= (πr²)h
Substituting 3.1416 for π (Fig. 10-36), 1 for r (calculated from Fig. 10-43.
D = 2 in., so r= 1 in.), and 8 for h (given in Fig. 10-43):
V= (3.1416)(12)(8) = 25.1328 cu. in.
STEP 3: To find the volume of the pipe, subtract the volume of the hole from the volume of the cylinder.
From STEP 1, the volume of the cylinder = 100.5312 cu. in. and from STEP 2, the volume of the hole = 25.1328 cu. in.
V = 75.3984 cu. in.
Example 3 calculating lateral and total area
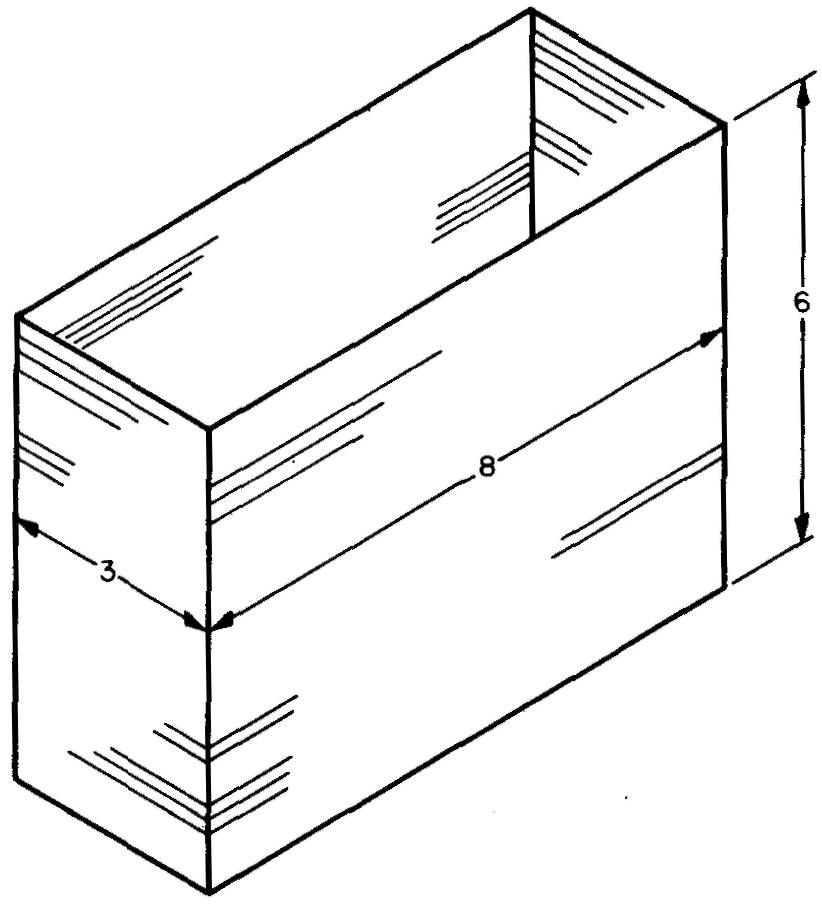
Calculate the lateral and total outside area of the sheet-metal tank shown in Fig. 10-44. The tank is open at the top.
Fig. 10-44
Solution
STEP 1: As shown in Fig. 10-41, Ls = ph. p = 2w + 21
Substituting this for p: L8= (2w + 2l)h.
Substituting 3 for w, 8 for /, and 6 for h (given in Fig. 10-44): L.= [(2)(3) + (2)(8)]6. Ls= 132 sq. in.
STEP 2: To find the total area, use the formula from Fig. 10-41: Ts = La + B. Remember this tank has one base.
To find B, use the formula: A = Iw.
Substituting this for B: Ts = Ls + Iw.
Substituting 132 for Ls (from STEP 1), 8 for / and 3 for w (given in Fig. 10-44): Ts= 132+ (8) (3). Ts = 156 sq. in.
Right pyramids and cones
A pyramid is a solid, usually with an equilateral plane figure for a base and three or more equilateral triangular faces which meet at a point called a vertex.
A right pyramid is a pyramid in which the vertex is in the line that is perpendicular to the center of its base. A right pyramid is shown in Fig. 10-45A.
Fig. 10-45. A pyramid and a cone
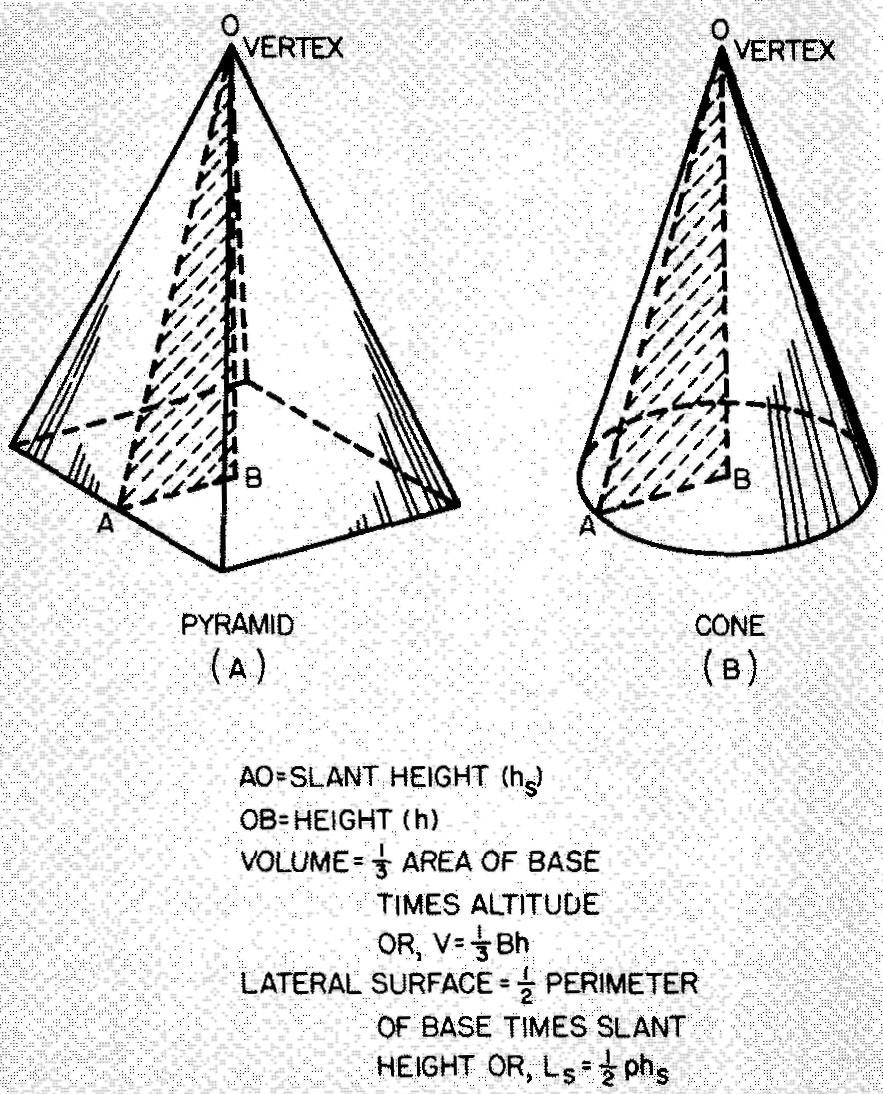
A cone is a solid figure which is formed by a lateral surface and a single base bounded by a circle. The vertex for a right cone lies on a line perpendicular to the base at the center of the base. Figure 10-45B shows a right cone.
Example 1 calculating volume and lateral area
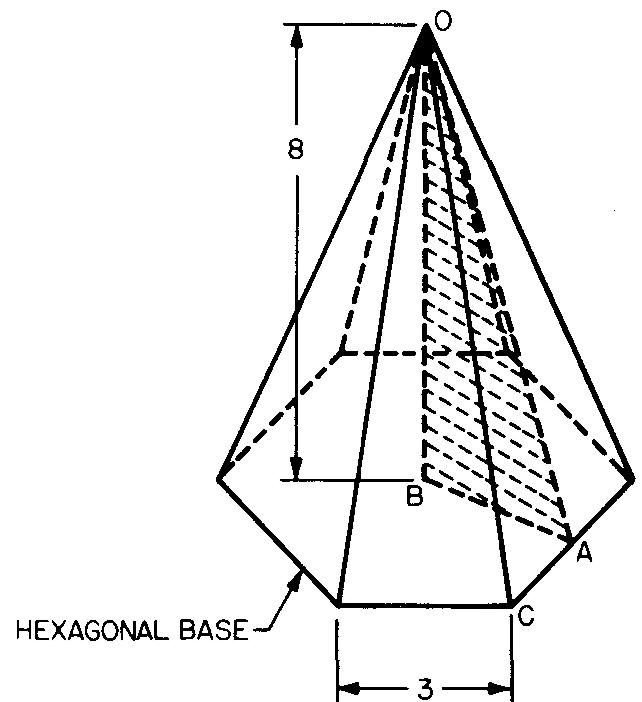
Calculate the volume and lateral area of the pyramid shown in Fig. 10-46.
Fig. 10-46
solution
STEP 1: As given in Fig. 10-45, V = 1/3 Bh.
To find B, use the formula from Fig. 10-12: A = 2.598s²
Substituting this for B: V= 1/3 (2.598s²) h.
Substituting 3 for s and 8 for h (given in Fig. 10-46):
V = 1/3(2.598)(3²) (8) = 62.352 cu. in.
STEP 2: To find the lateral area (Ls), use the formula given in Fig. 10-45: Ls = 1/2 phs.
The slant height (hs) can be found by finding the length of the hypotenuse of shaded triangle A OB in Fig. 10-46.
To find hs, use the formula c =√(a2 + b2)
Let line AB = a, BO = b, and AO = c.
From information given in Figs. 10-46 and 10-12, a = 1/2 f. Figure 10-12 gives f = 1.732s
Substituting 3 for s (given in Fig. 10-46):
f = (1.732)(3) = 5.196.
Substituting for f in a = 1/2 f:
a= (1/2)(5.196) = 2.598 in.
Substituting 2.598 for a and 8 for b (given in Fig. 10-46):
c = √(2.598² + 8) = 8.41 in.
STEP 3: To find the lateral area (Ls), use the formula: Ls = 1/2 phs.
To find p, multiply s by the number of sides.
From Fig. 10-46, 5 = 3 in. and there are 6 sides, so p = 18.
Substituting 18 for p and 8.41 for hs (from STEP 2):
Ls = (1/2) (18) (8.41) = 75.69 sq. in.
Example 2 calculating volume and lateral area
Calculate the volume and lateral area of the cone shown in Fig. 10-47.
Fig. 10-47
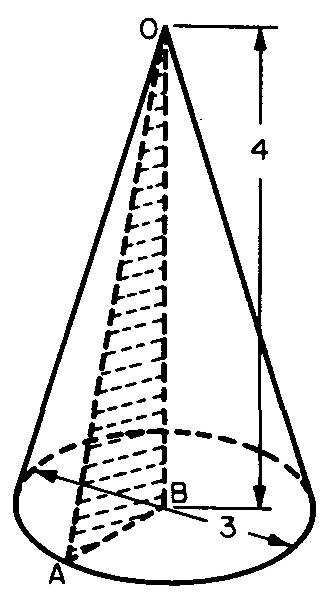
Solution
STEP 1: To find the volume, use the formula from Fig. 10-45: V= 1/3 Bh.
To find B, use the formula from Fig. 10-36: A = πr².
Substituting this for B: V = 1/3(πr²)h.
Substituting 3.1416 for it (Fig. 10-36), 1.5 for r (calculated from Fig. 10-47. D = 3 in., so r= 1.5 in.), and 4 for h (given in Fig. 10-47):
V= 1/3(3.1416) (1.5²) (4) = 9.4248 cu. in.
STEP 2: To find the lateral area (Ls), use the formula Ls = 1/2 phs.
The slant height (hs) is the hypotenuse of the shaded triangle AOB in Fig. 10-47.
c = √(a² + b²)
Substituting 1.5 for a and 4 for b:
c = √(1.5² + 4²)
c = 4.27 in.
To find p, use the formula from Fig. 10-36, C = πD.
Substituting 3.1416 for π (Fig. 10-36) and 3 for D (given in Fig. 10-47):
C = (3.1416) (3) = 9.4248 in.
Substituting 9.4248 for p and 4.27 for h8:
L8 = (9.4248) (4.27) / 2 = 20.1219 sq. in.
Tapers
When a machine part tapers, the draftsman may need to compute the amount of taper per inch. At other times he may need to compute the amount of taper for the length of the part.
On other occasions the draftsman may know the amount of taper and the measurement of one diameter and may need to compute the measurement of the other diameter.
The following examples illustrate computations needed for these differing situations.
Example 1 calculating the amount of taper
The taper per inch on a piece of work is 0.05 inch. What is the taper in 8 inches?
Solution
The taper is 0.05 inch for every inch. Thus the taper in 8 inches is 8 times 0.05 inch.
Taper = (8) (0.05), or 0.4 in.
Example 2 calculating the amount of taper
What is the taper per inch if the taper per foot is 5/8 inch?
Solution
The taper is 5/8 inch for every foot. Thus the taper per inch is 1/12 of 5/8 inch.
Taper per inch = 0.625 / 12, or 0.052 in.
Example 3 calculating the amount of taper
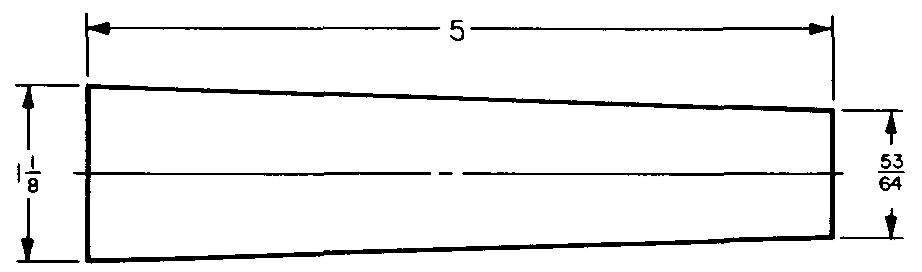
Calculate the taper per foot for Fig. 10-48.
Fig. 10-48
Solution
Taper of piece = D - d.
Substituting 1.125 for D and 0.828125 for d (given in Fig. 10-48):
Taper of piece = 1.125 - 0.828125.
Taper of piece = 0.296875.
Taper per inch = Taper divided by length.
Substituting 0.296875 for taper of piece and 5 for length of piece (given in Fig. 10-48):
Taper per inch = 0.296875 / 5.
Taper per inch = 0.059357 in.
Taper per foot = 12 X Taper per inch.
Taper per ft. = (12) (.059357), or 0.7125 in.
Example 4 calculating the diameter
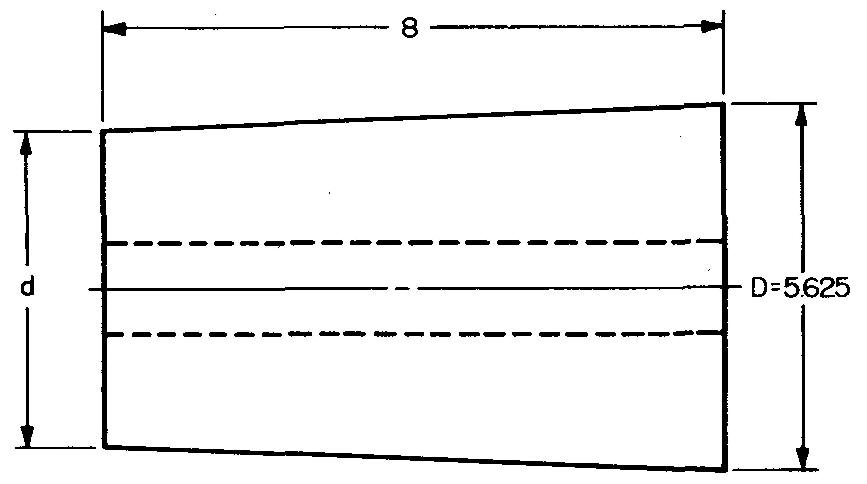
Calculate the small diameter of Fig. 10-49. The taper is 0.6 inch per foot.
Fig. 10-49.
Solution
Taper per inch = Taper per foot divided by 12.
Taper per inch = 0.6/12, or 0.05 in.
Taper in 8 inches = (8) (0.05), or 0.4 in.
d = D - Taper
Substituting 5.625 (given in Fig. 10-49) for D and 0.4 for Taper:
d = 5.625 - 0.4 = 5.225 in.
Example 5 calculating the diameter
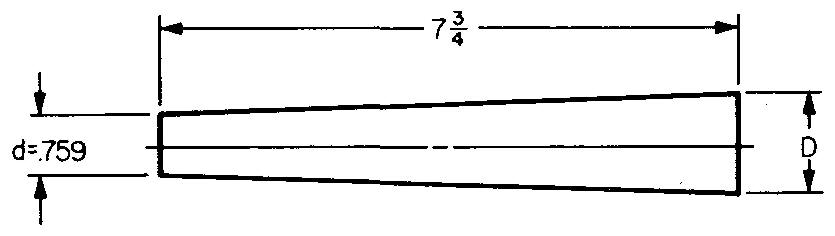
Calculate the large diameter of Fig. 10-50. The taper is 1/16 inch per inch.
Fig. 10-50
Solution
Taper = Taper per inch times length of piece.
Taper = 0.0625 X 7.75, or 0.484275 in. D = d + Taper.
Substituting 0.759 for d (given in Fig. 10-50) and 0.484275 for Taper: D = 0.759 + 0.484275, or 1.243275 in.
Problems: review of drafting mathematics (Answers are not given)
These review problems in this section illustrate some of the more common, everyday types of mathematics problems a machine draftsman should be able to solve.
For each problem, work out the answers for the missing dimensions which are represented by letters.
Remember that a freehand sketch will often be a great aid in setting up the problem and in finding the solution for the problem.
Some of the problems involve screw threads.
Certain symbols and terms listed in these problems may not be clearly understood. It is suggested that before starting these problems, the student refer to section 12 (Basic machining operations) for this information
|
problem 10-1
|
problem 10-2
|
problem
10-3 |
problem
10-4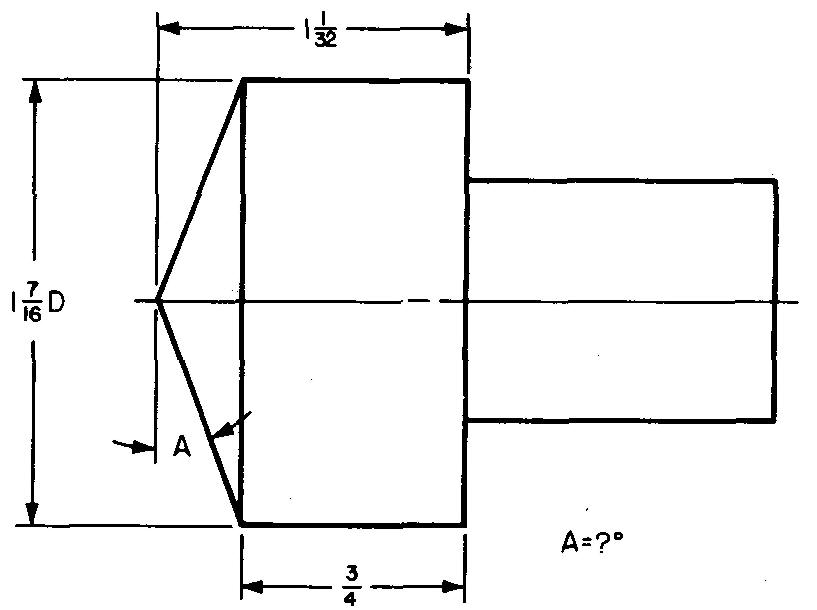 |
problem
10-5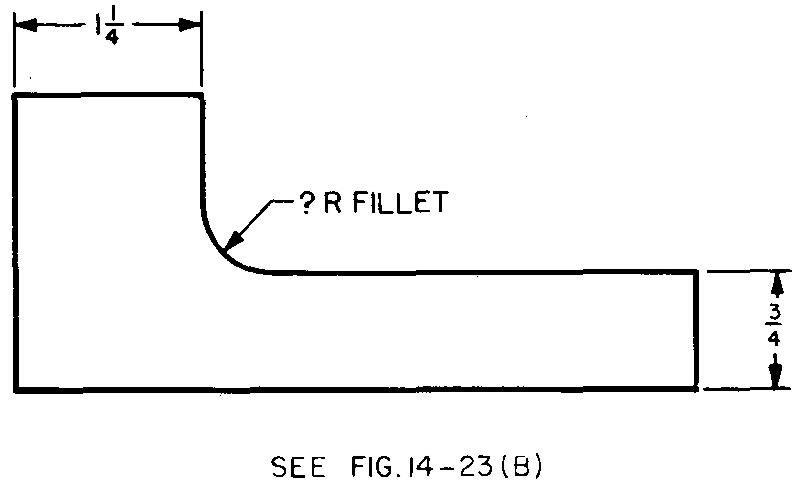 |
problem
10-6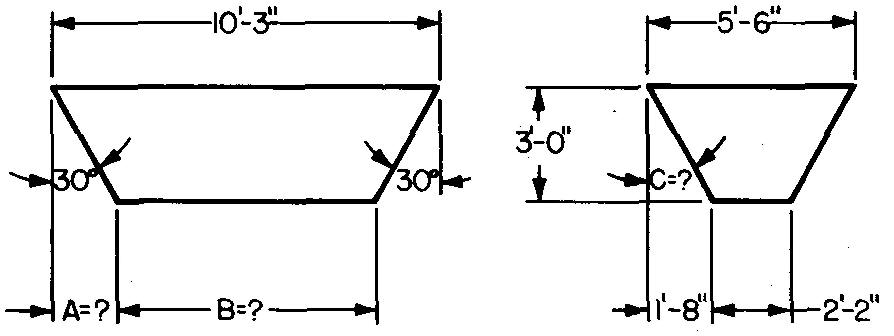 |
problem
10-7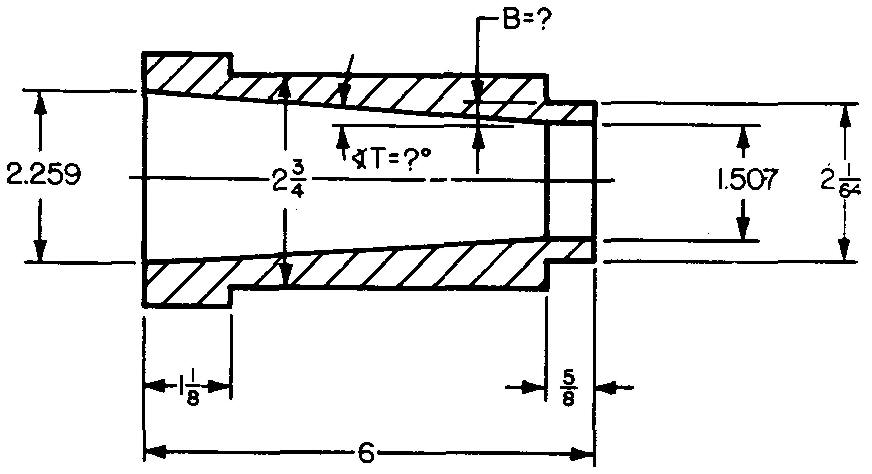 |
problem
10-8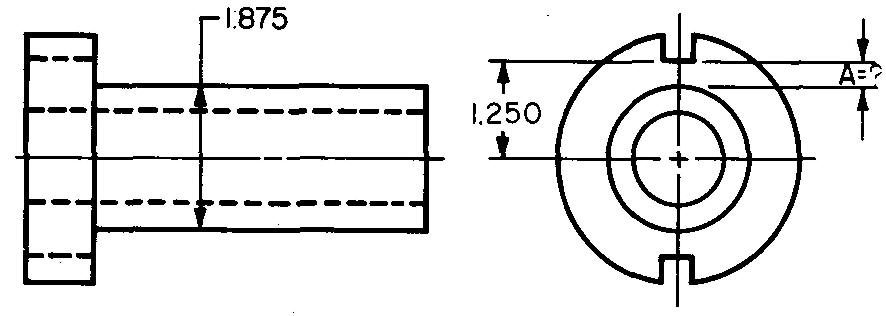 |
problem
10-9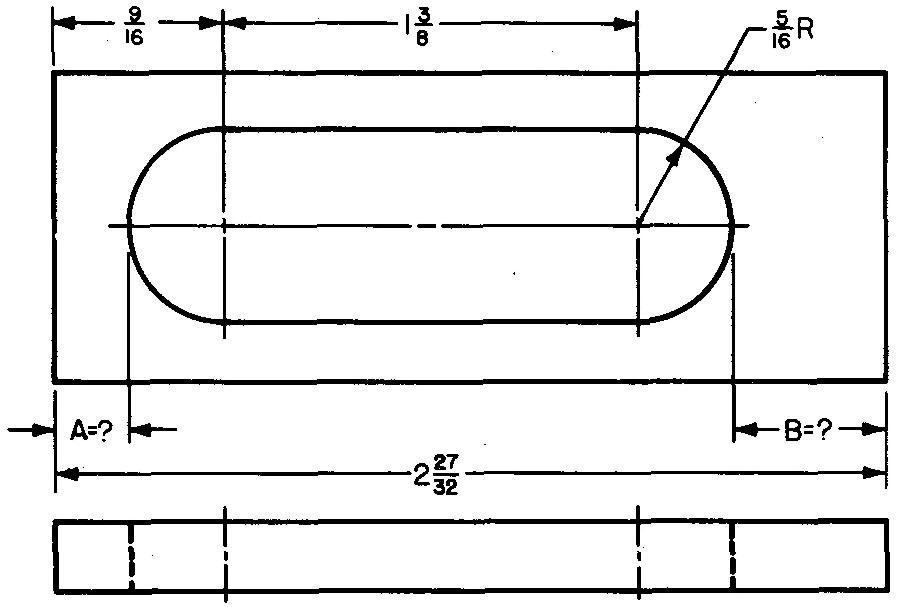 |
problem
10-10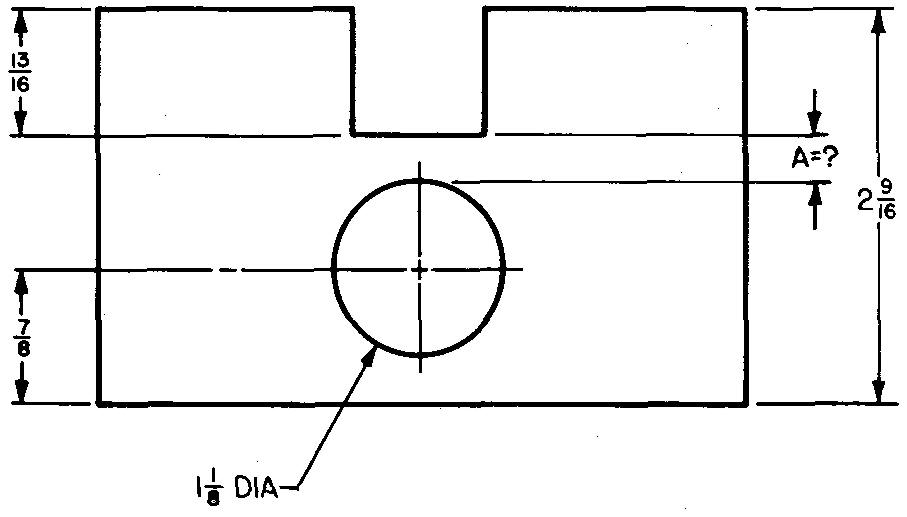 |
problem
10-11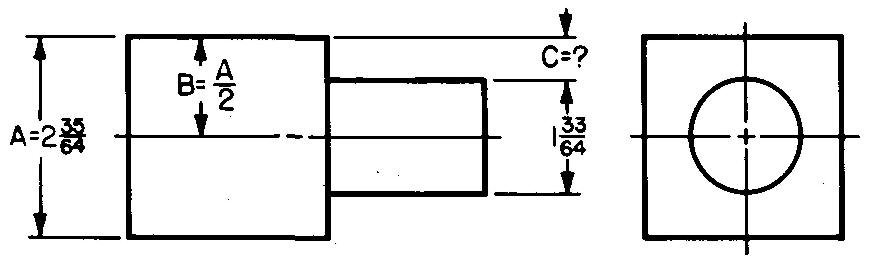 |
problem
10-12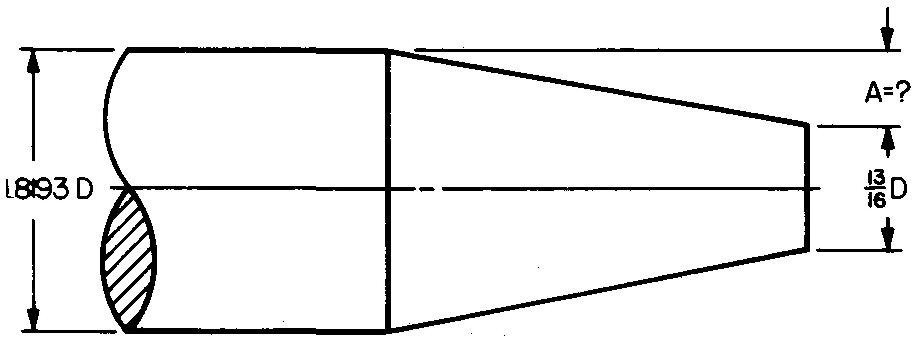 |
problem
10-13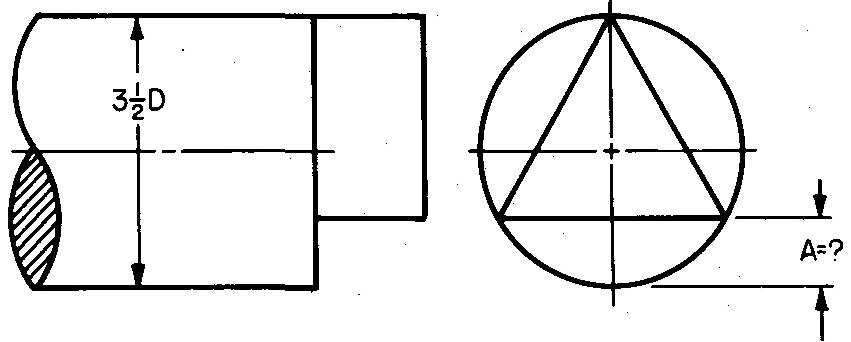 |
problem
10-14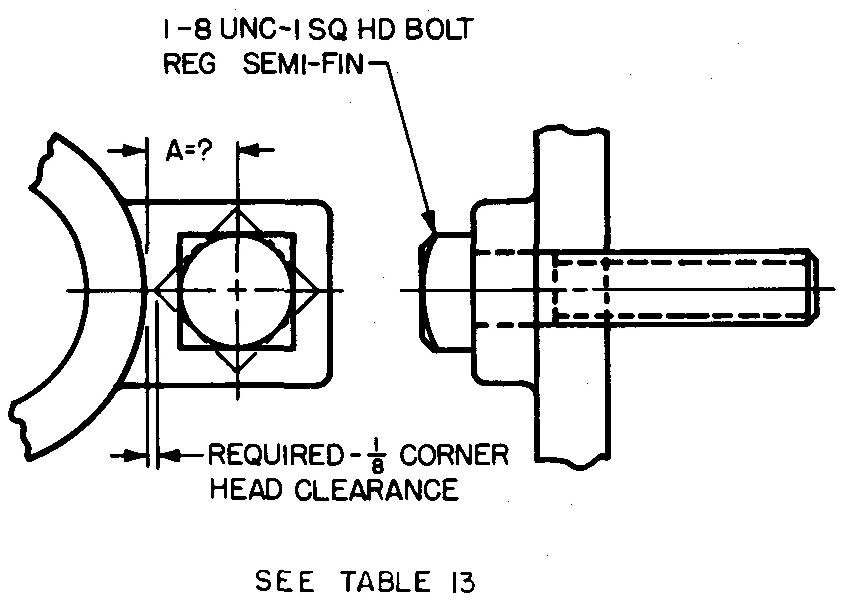 |
problem
10-15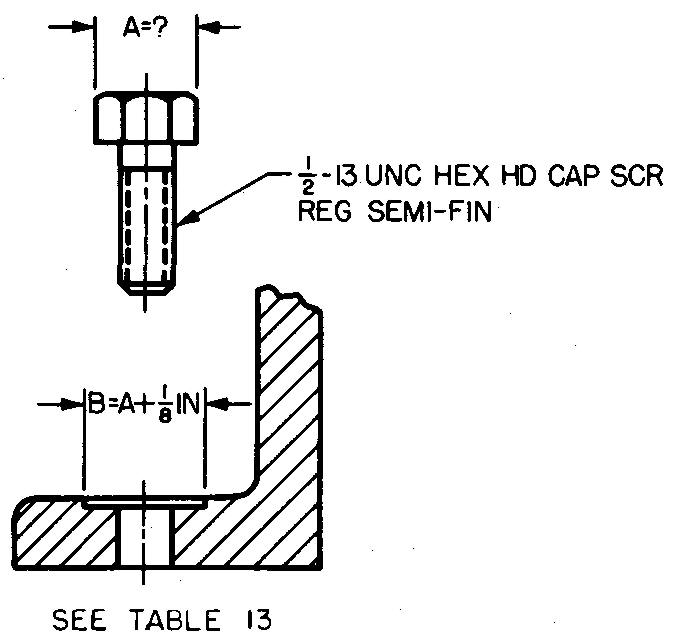 |
problem
10-16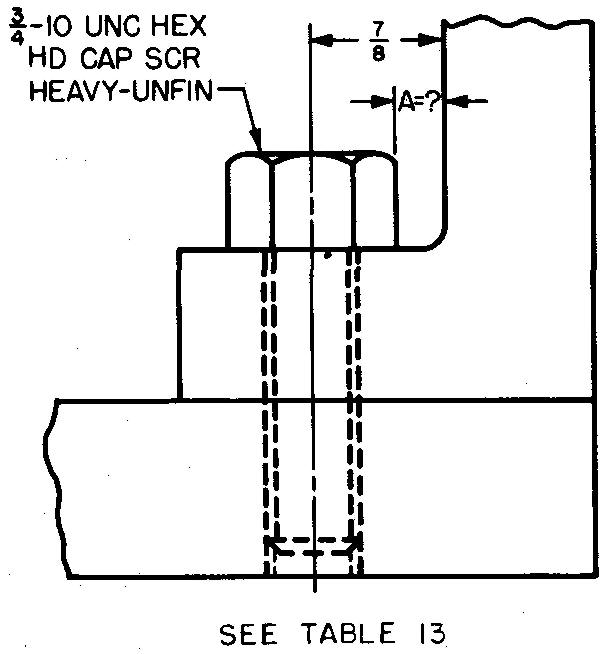 |
problem
10-17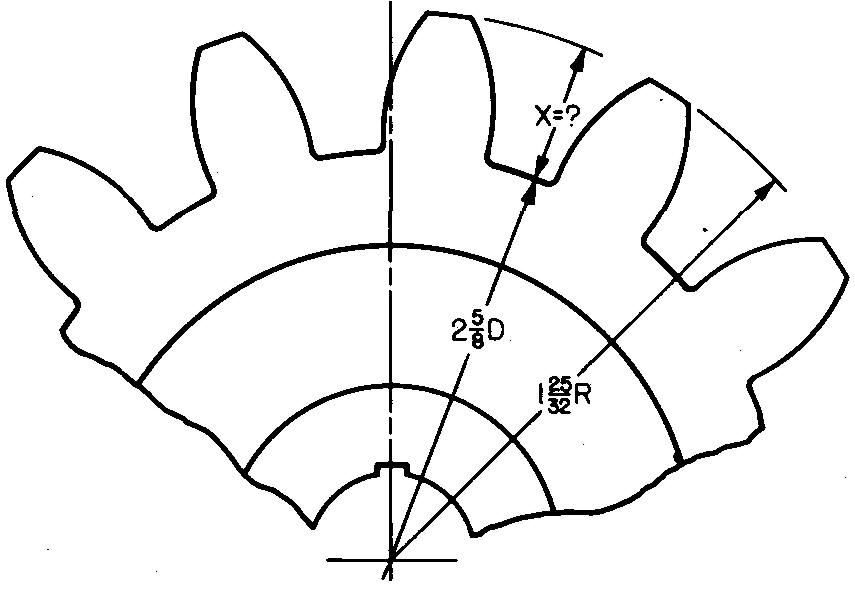 |
problem
10-18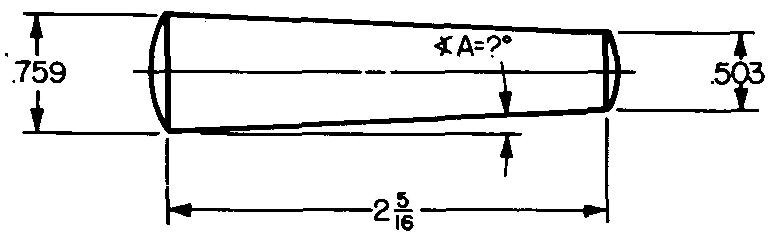 |
problem
10-19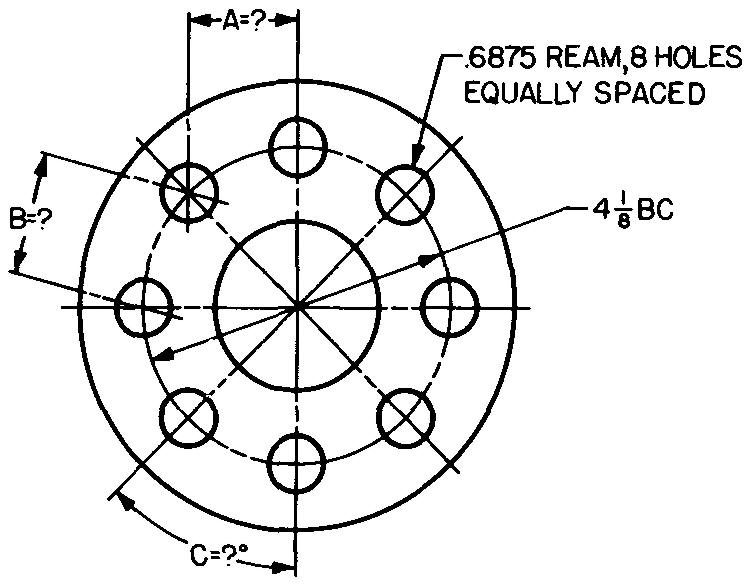 |
problem
10-20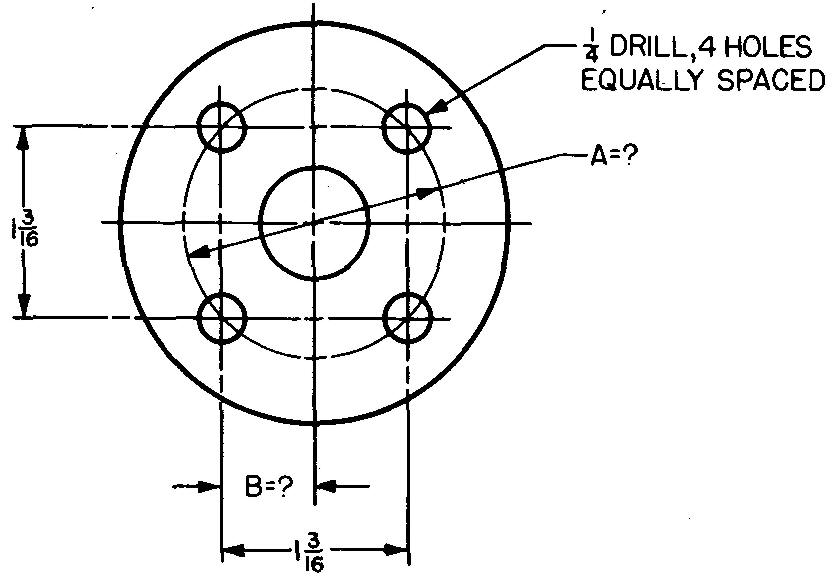 |
problem
10-21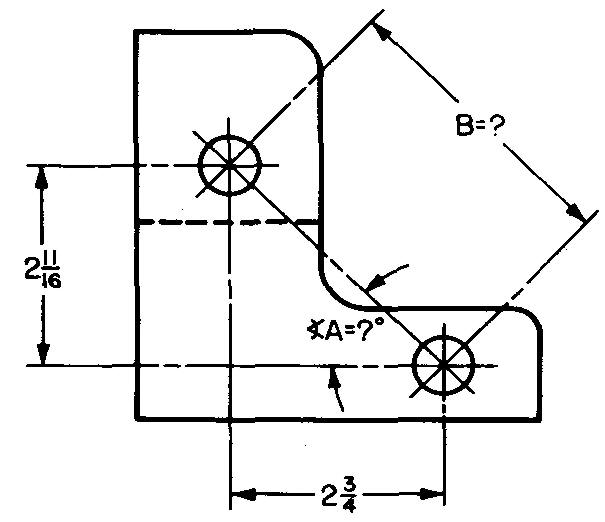 |
problem
10-22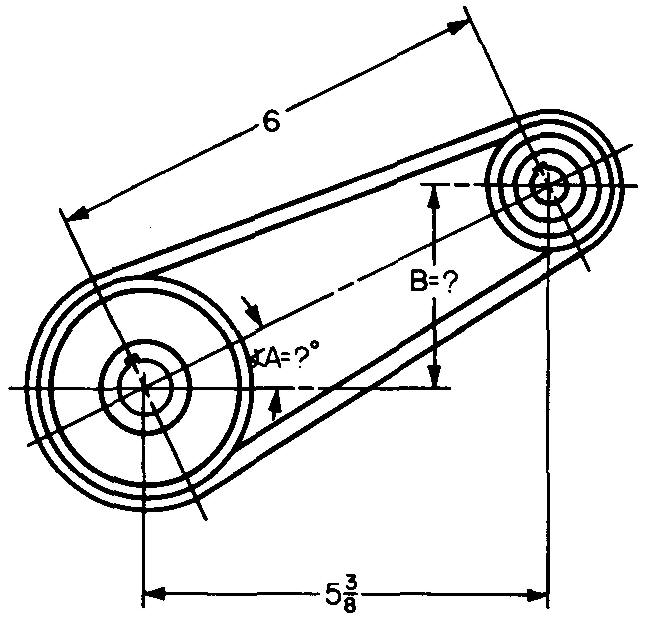 |
problem
10-23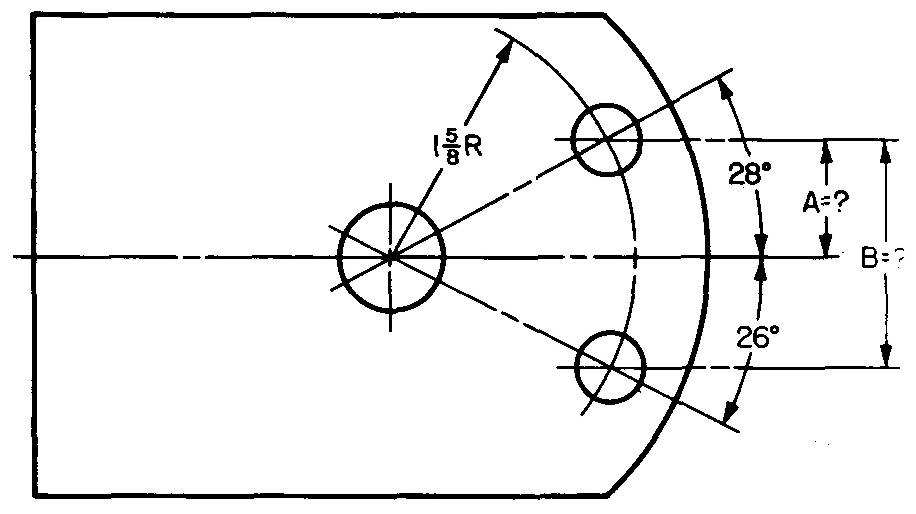 |
problem
10-24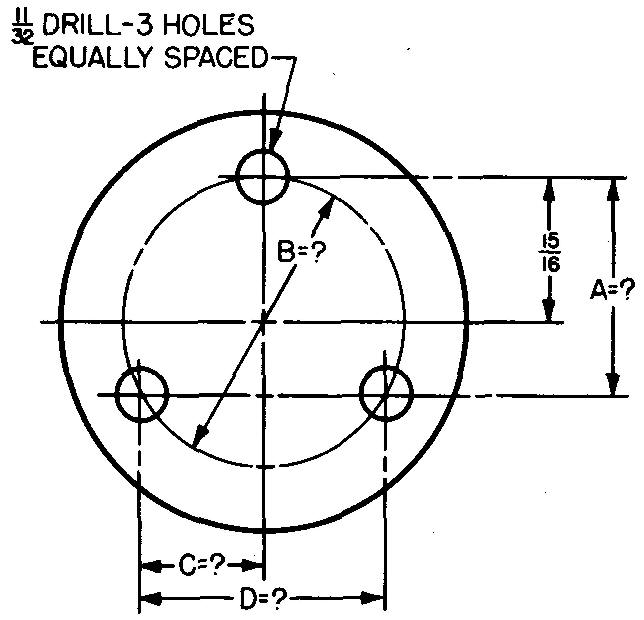 |
problem
10-25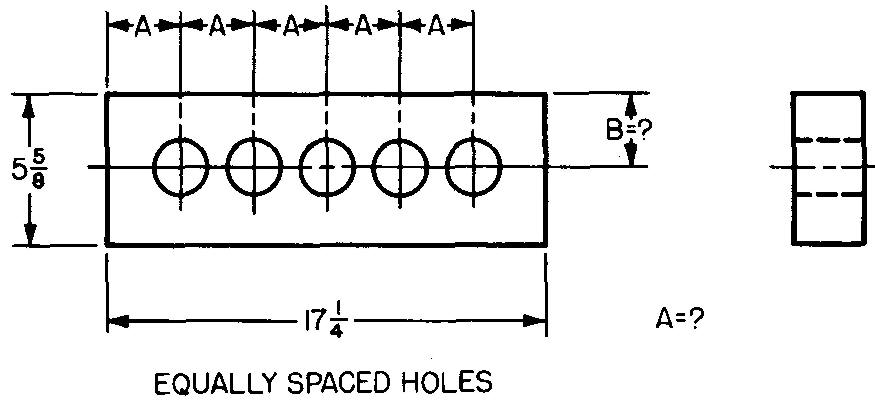 |
problem
10-26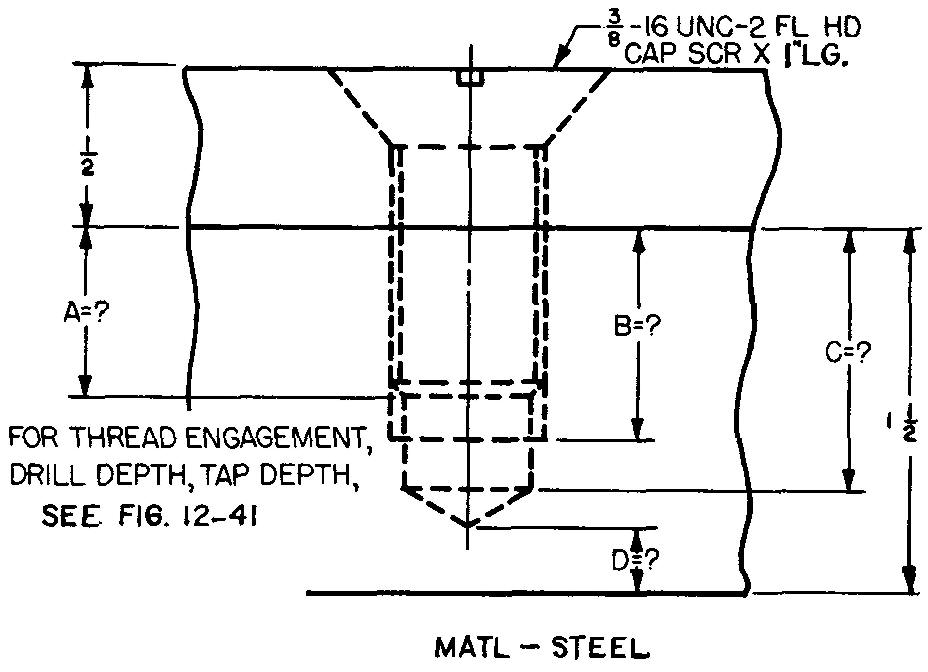 |
problem
10-27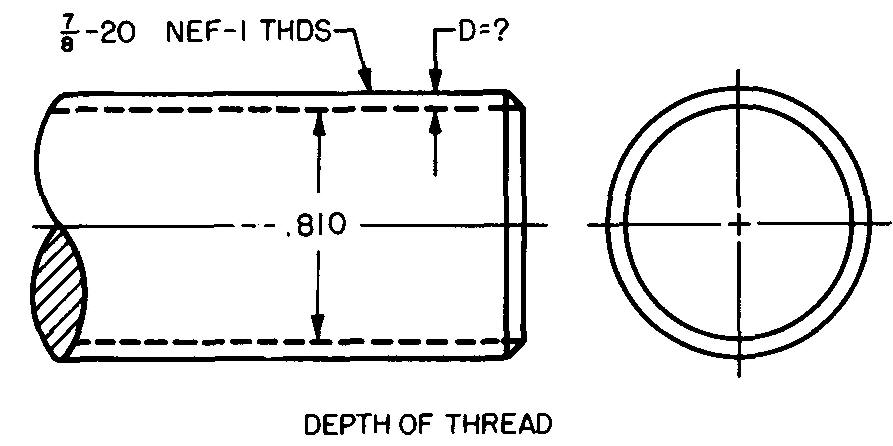 |
problem
10-28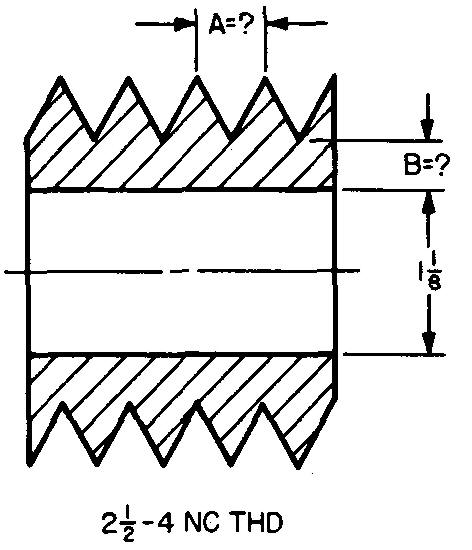 |
problem
10-29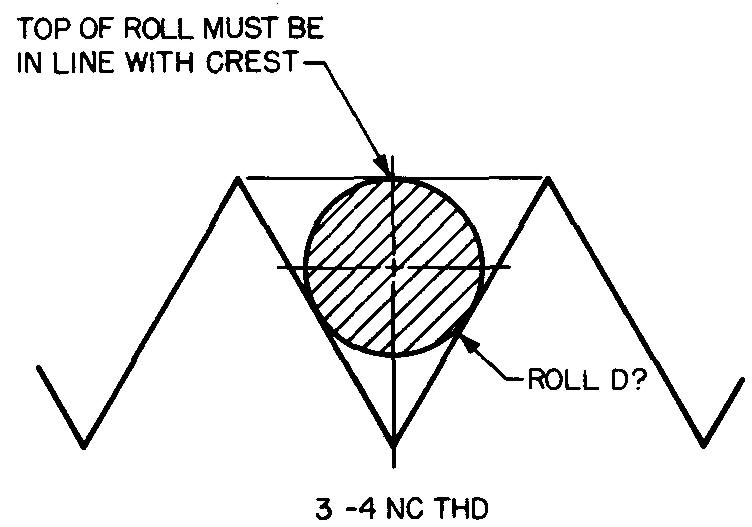 |
problem
10-30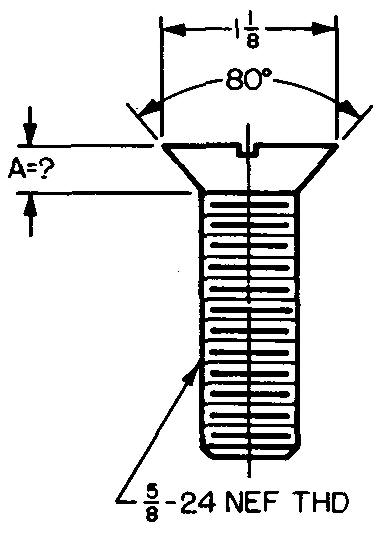 |
problem
10-31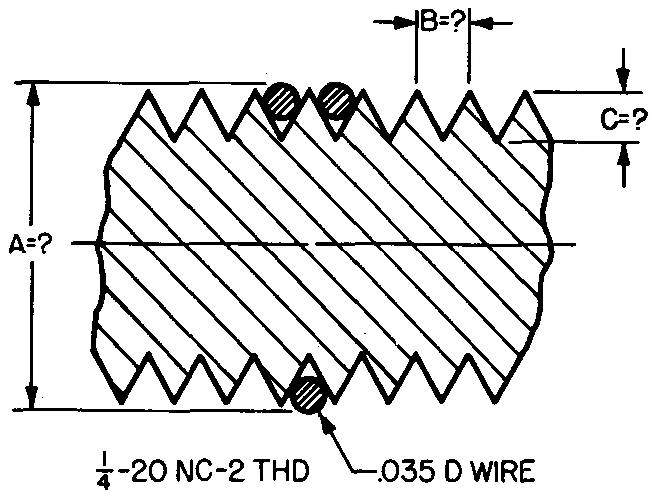 |
problem
10-32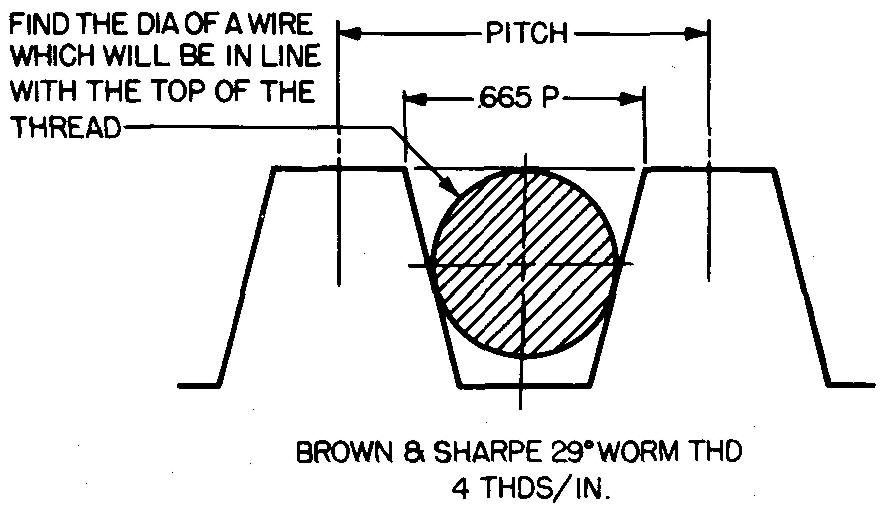 |
problem
10-33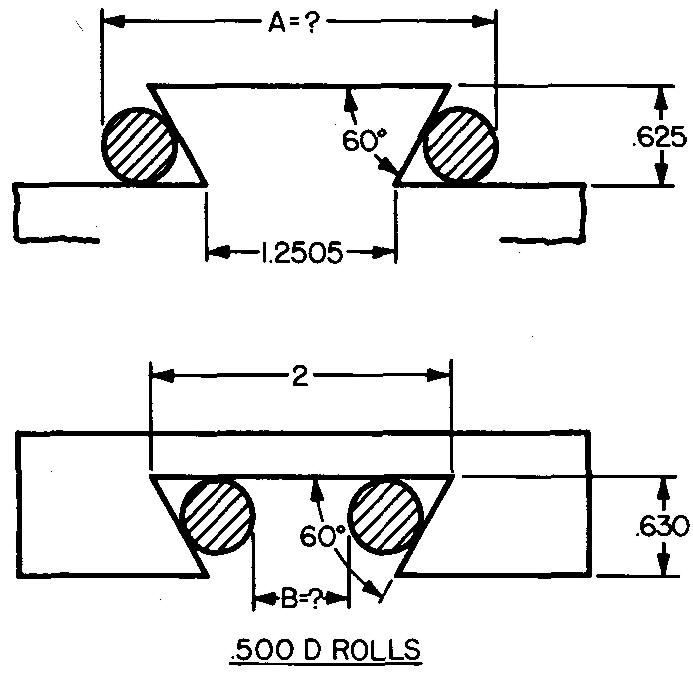 |
problem
10-34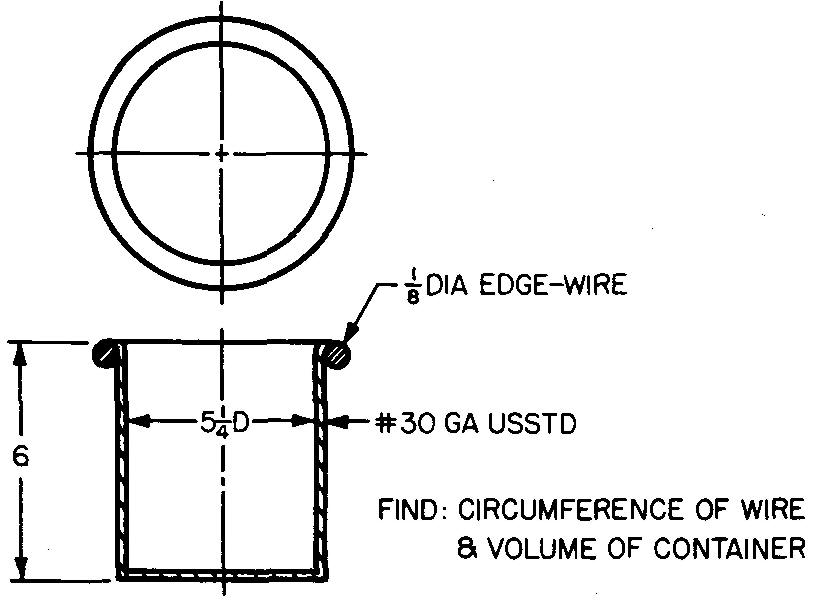 |
problem
10-35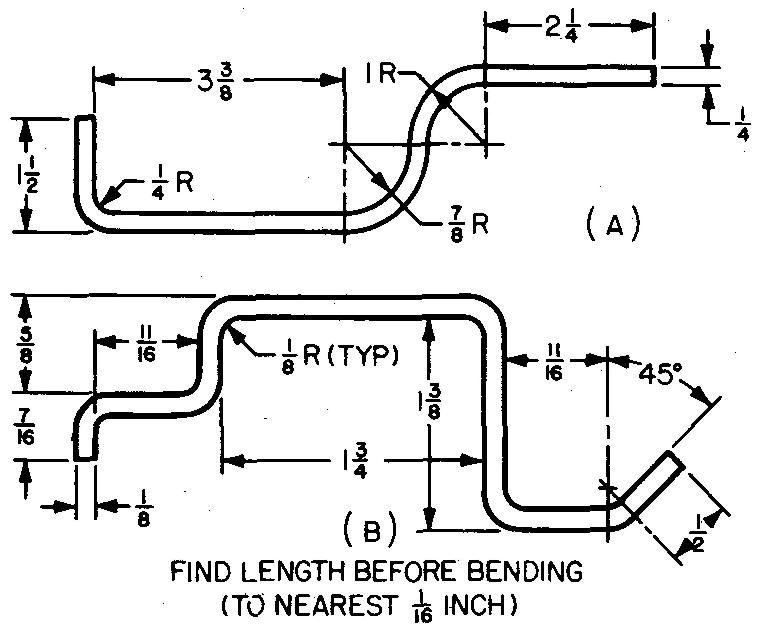 |
problem
10-36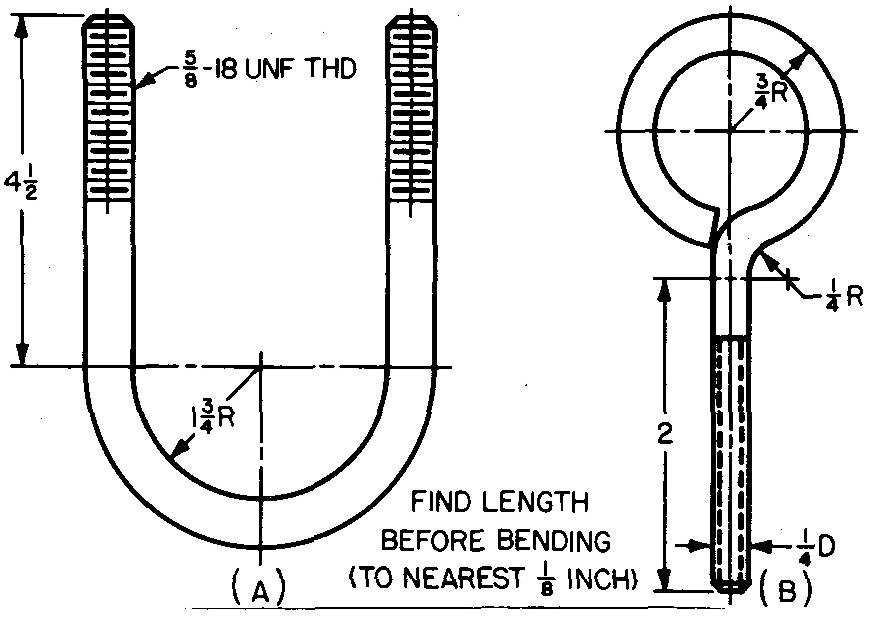 |
