Décodeurs (Sélecteur)
Voir aussi : Sélecteur, Verrouilleur et Registre
| Sélecteur RTL à deux entrées | Sélecteur DTL à deux entrées |
| Sélecteur TTL (Porte ET) | Sélecteur TTL (Porte ET, NON-OU, NON-ET) |
Les décodeurs sont des circuits combinatoires qui convertissent les entrées binaires d'une forme à une autre. Il y a 'n' lignes d'entrée qui peuvent générer des lignes de sortie de 2n.
Si l'entrée présente des conditions indifférentes, alors toutes les lignes de sortie de 2n ne sont pas utilisées.
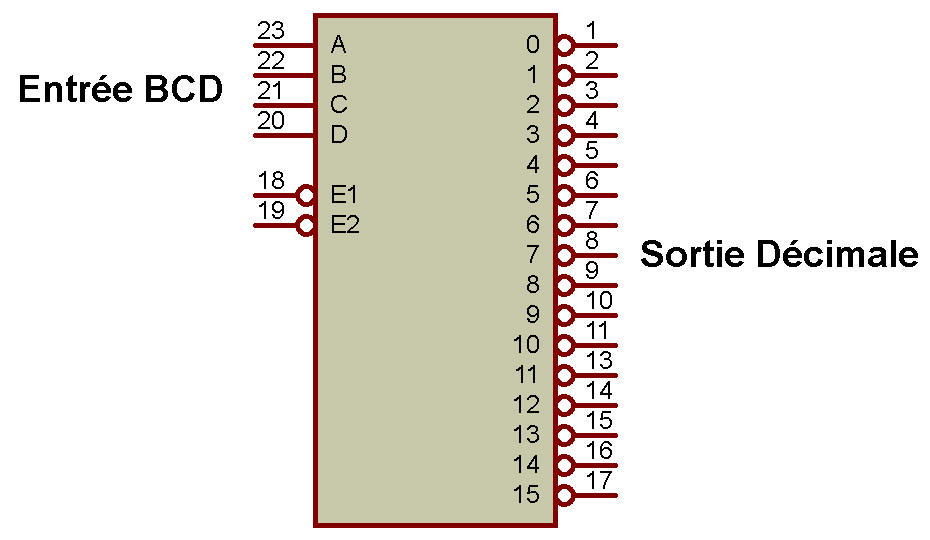
Par exemple, le décodeur BCD vers décimal dispose de 4 lignes d'entrée pouvant générer 24 = 16 sorties, mais seules 9 lignes de sortie sont utilisées.
La structure générale du circuit décodeur n : 2n est illustrée à la figure ci-dessous:

Quelques exemples de décodeurs sont le décodeur binaire à octal (3 lignes d'entrée et 8 lignes de sortie) également appelé décodeur 3 lignes à 8 lignes, BCD à décodeur décimal, BCD à décodeur à 7 segments.
BCD to 7 segments logique diagramme Les afficheurs à Segments (LED)
Décodeur binaire vers octal
Le décodeur binaire vers octal dispose de 3 lignes d'entrée et de 8 lignes de sortie.
Les entrées sont désignées par : I0, I1, I2 et I3 et les sorties par : D0, D1, D2, D3, D4, D5, D6 et D7.
La table de vérité est présentée dans le tableau ci-dessous:
| Table de vérité du décodeur binaire à octal | ||||||||||
| Entrées | Sorties | |||||||||
| I2 | I1 | I0 | D7 | D6 | D5 | D4 | D3 | D2 | D1 | D0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
D'après la table de vérité, il est clair que,
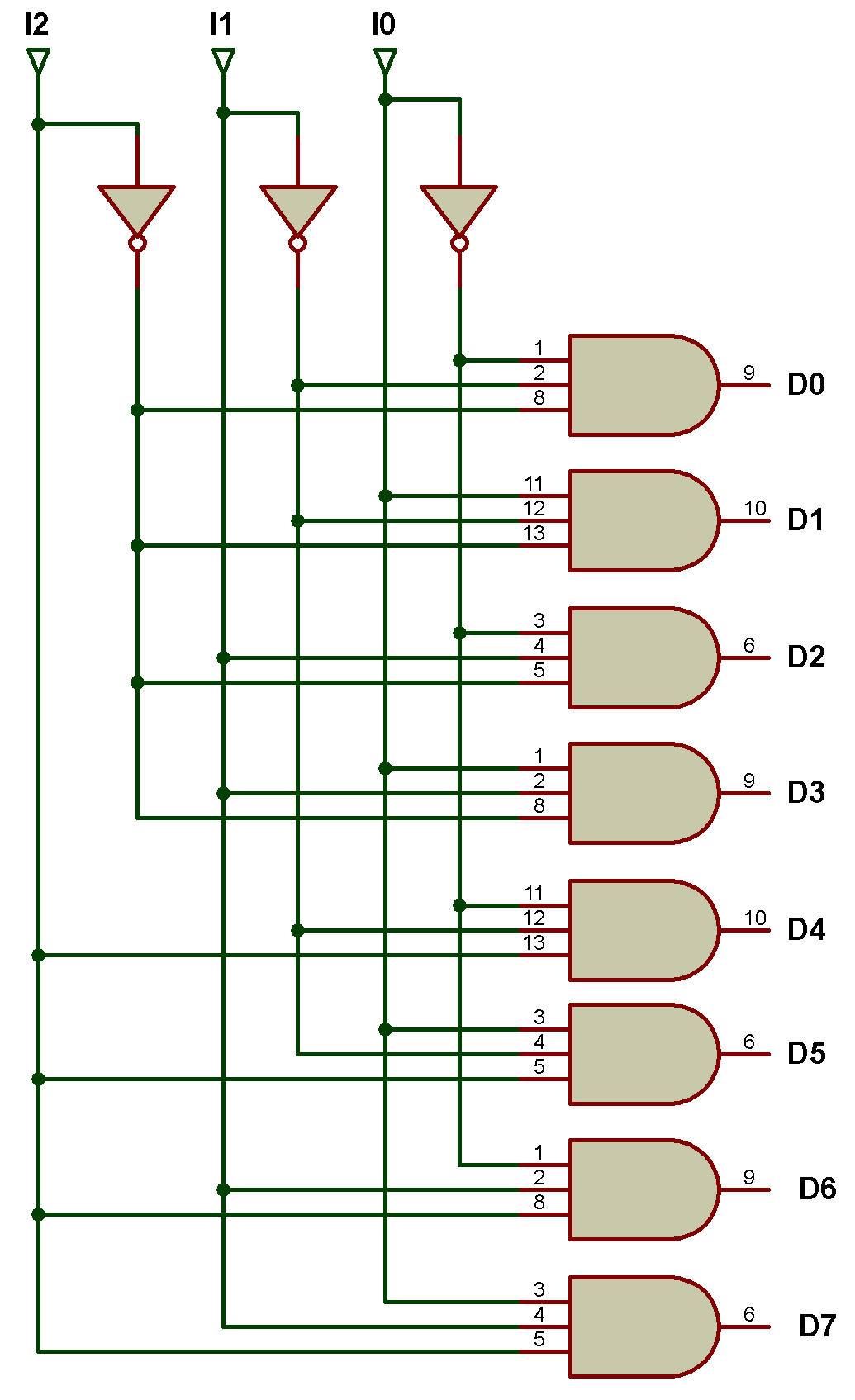
D0 = I2'I1'I0' D1 = I2'I1'I0 D2 = I2'I1I0' D3 = I2'I1I0
D4 = I2I1'I0' D5 = I2I1'I0 D6 = I2I1I0' D7 = I2I1I0
Le schéma logique du décodeur binaire à octal est présenté dans la figure ci-dessous:
Implémentation/conception d'un circuit combinatoire à l'aide d'un décodeur
Discutons de la façon d'implémenter/concevoir un additionneur complet à l'aide d'un décodeur.
Nous savons que les décodeurs ont 'n' lignes d'entrée et peuvent générer des lignes de sortie de 2n.
Tout circuit combinatoire peut être implémenté à l'aide d'un décodeur (décodeur de ligne n à 2n) si le circuit combinatoire peut être exprimé sous la forme d'une somme de termes.
Ensuite, le circuit logique peut être dessiné à l'aide de la porte OR.
La table de vérité du Full Adder est présentée dans le tableau ci-dessous:
| Entrées | Sorties | |||
| X | Y | Zin | S(Somme) | Cout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Les termes pour les sorties S et C sont :
S(X, Y, Z) = Σ(1, 2, 4, 7) et C(X, Y, Z) = Σ(3, 5, 6, 7)
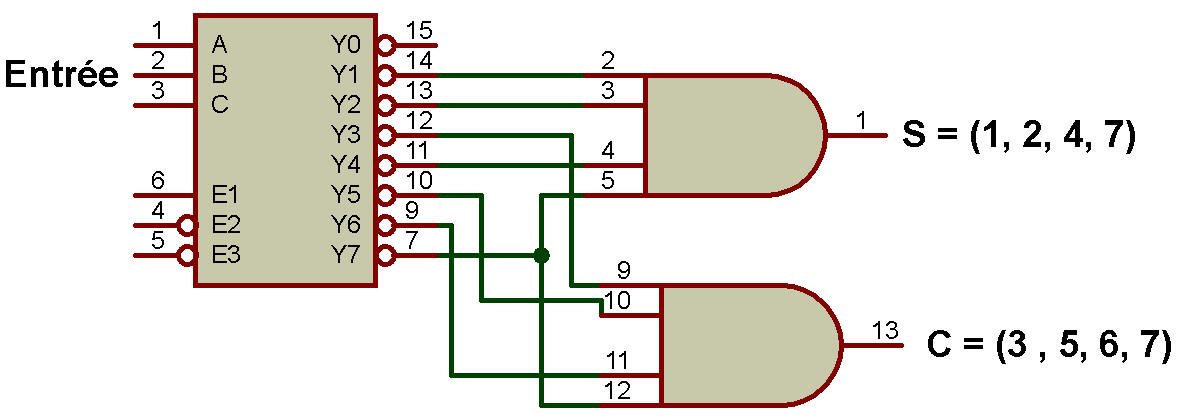
Nous avons 3 entrées X, Y et Z et 8 sorties, 4 pour S(X, Y, Z) = Σ(1, 2, 4, 7) et 4 pour C(X, Y, Z) = Σ(3 , 5, 6, 7).
Nous avons besoin de 2 portes OR - une pour les minterms de S et l'autre pour les minterms de C.
L'implémentation de Full Adder à l'aide du décodeur est illustrée dans la figure ci-dessous:
Le décodeur peut être utilisé pour mettre en œuvre la plupart des circuits
combinatoires. La mise en œuvre de tout circuit combinatoire utilisant un
décodeur est utile par rapport à une autre méthode de mise en œuvre de ce
circuit combinatoire si la mise en œuvre du décodeur fournit la meilleure mise
en œuvre (en termes de coût et de complexité du circuit). Si le circuit
combinatoire a de nombreuses sorties et que chaque sortie peut être exprimée en
termes d’un petit nombre de termes, alors la mise en œuvre du décodeur de ce
circuit combinatoire est l’une des meilleures implémentations.
2.3.10.3
Extension du décodeur (décodeur en cascade)
Deux ou plusieurs petits
décodeurs peuvent être mis en cascade pour créer un décodeur plus grand. Il y a
une autre entrée supplémentaire connectée à la ligne d’entrée du décodeur. Cette
entrée est E (Enable) et est utilisée pour activer et désactiver un décodeur
particulier. L'exemple 1 montre comment construire un décodeur 4 x 16 en
utilisant (en cascade) deux décodeurs 3x8.
La figure ci-dessous montre l'implémentation et l'exemple 2 montre comment construire un décodeur 4x16 en utilisant (en cascade) quatre décodeurs 2x4.
Exemple 1 : Création d'un décodeur 4x16 en utilisant (en cascade) deux décodeurs 3x8.
Solution:
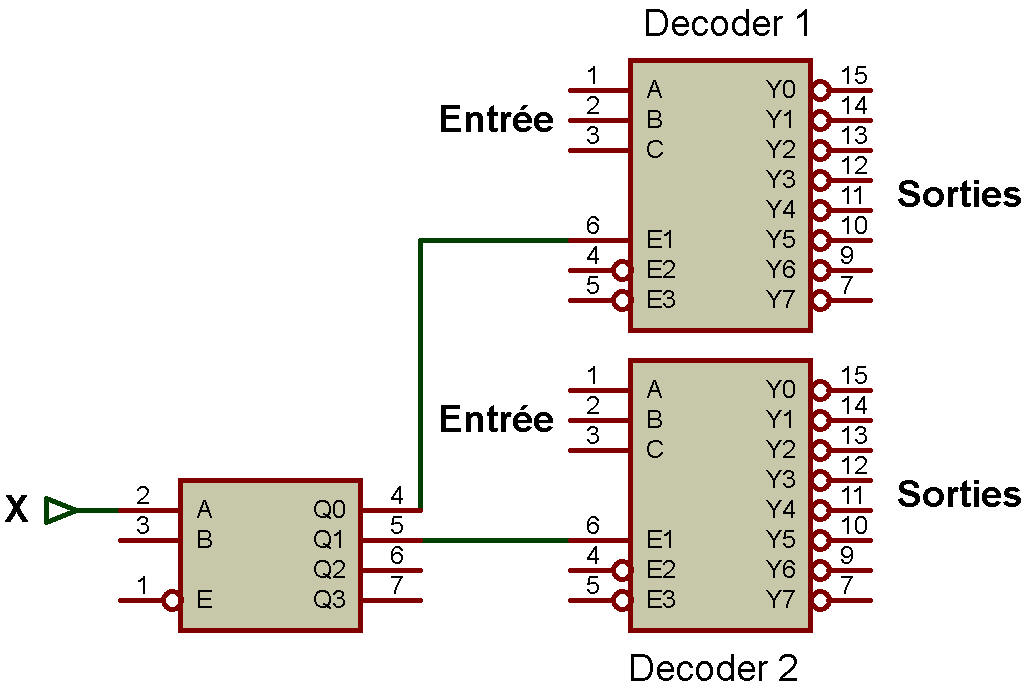
Comme le montre la figure, il existe deux décodeurs 3x8 : le décodeur 3x8 (1) et le décodeur 3x8 (2).
Il existe également un décodeur 1x2. Ce décodeur 1x2 permet de sélectionner l'un des décodeurs 3x8.
Lorsque le décodeur 1x2 produit Q0 = 1, alors le décodeur 3x8 (1) est sélectionné (activé) et lorsque le décodeur 1x2 produit Q1 = 1, alors le décodeur 3x8 (2) est sélectionné.
Exemple 2 : Création d'un décodeur 4x16 en utilisant (en cascade) quatre décodeurs 2x4.
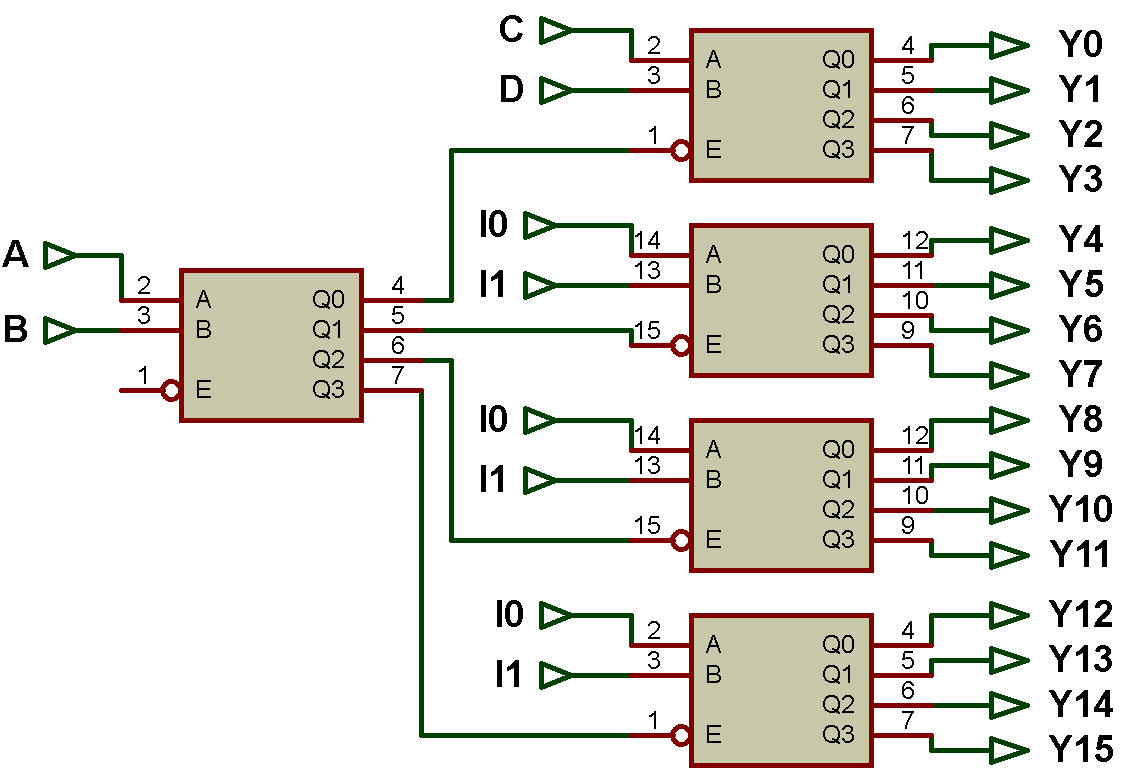
Comme le montre la figure, il existe cinq décodeurs 2x4 : décodeur 2x4 (1), décodeur 2x4 (2), décodeur 2x4 (3) et décodeur 2x4 (4) et décodeur 2x4 (5).
Le décodeur 2x4 (1) permet de sélectionner l'un des quatre autres décodeurs 2x4.
Lorsque le décodeur 2x4 (1) produit Q0 = 1, alors le décodeur 2x4 (2) est sélectionné (Activé)
et, lorsque le décodeur 2x4 (1) produit Q1 = 1, alors le décodeur 2x4 (3) est sélectionné,
lorsque le décodeur 2x4 (1) produit Q2 = 1, alors le décodeur 2x4 (4) est sélectionné
et lorsque le décodeur 2x4 (1) produit Q3 = 1, alors le décodeur 2x4 (5) est sélectionné.
