Simplification de la fonction booléenne
Introduction :
Par simplification des fonctions booléennes, nous entendons minimiser le nombre de termes utilisés pour représenter une fonction booléenne.
Une simplification de la fonction booléenne est requise afin de réduire la complexité du matériel utilisé pour mettre en œuvre la fonction booléenne. La simplification garantit également des résultats fiables.
La simplification des fonctions booléennes peut être effectuée en utilisant l'une des méthodes suivantes :
Méthode de simplification algébrique
Méthode Veitch-Karnaugh (K-Map)
Méthode graphique de Quine-McCluskey.
Nous discuterons de chacune de ces méthodes une par une.
Méthode de simplification algébrique
Dans la méthode de simplification algébrique de la fonction booléenne, la simplification se fait en appliquant divers postulats et théorèmes booléens afin de réduire le nombre de termes utilisés dans la fonction booléenne.
La simplification algébrique a déjà été abordée la section Fonctions booléennes et leur représentation, mais nous prendrons tout de même quelques exemples dans cette section pour rappeler la méthode de simplification booléenne.
Exemple:
Simplifiez la fonction booléenne F1 = (xy' + x'y') . (xz') en utilisant la méthode de simplification algébrique.
Solution : F1 = (xy' + x'y') . xz')
Soient xz' =a, xy' =b et x'y' =c
Donc, F1 = (b + c) . (a) = (a . b) + (a . c) — Loi distributive de Hising
En remplaçant les valeurs de a,b et c, nous obtenons,
F1 = (xz'.xy') + (xz'.xy) =xy'z' + 0 ->en utilisant le théorème l(b)
x . x= 1 et le postulat 5(b) x . x' = 0 = xy'z'
D'après l'exemple, il ressort clairement que la simplification réduit le nombre de termes utilisés dans la fonction booléenne F1.
Avant la simplification, il y avait trois termes dans F1 soit xy', x'y' et xz'.
Le schéma logique pour implémenter F1 avant simplification nécessite 8 portes logiques.
Après simplification, il n'y a qu'un seul terme dans F1 et c'est xy'z'.
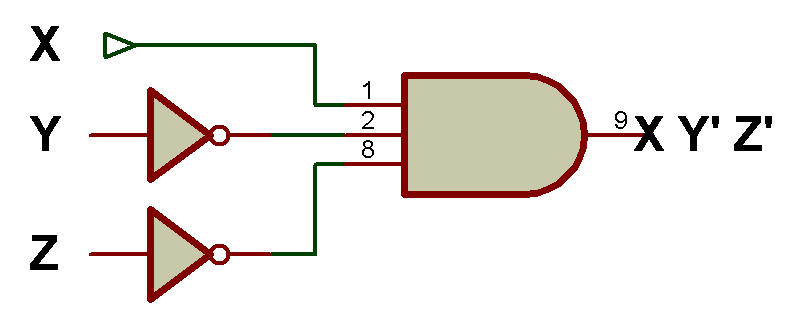
Le schéma logique pour implémenter F1 est simple et nécessite également moins de portes logiques (seulement 3 portes) comme le montre la figure ci-dessous:
Schéma logique pour implémenter F1 après simplification

Exemple:
Simplifiez la fonction booléenne F2 = xyz + xy'z + x'yz' +xy'z' + xz' en utilisant la méthode de simplification algébrique.
Solution :
F2 = xyz + xy'z + x'yz' +xy'z' + xz' = xz(y + y') + x'yz' + xz'(y' + 1)
= xz +x'yz' + xz'
-> y + y' =1 [Postulat 5(a)]
et y' +1 =1 [Théorème 2(a)]
= xz + xz' + x'yz'
= x(z + z') + x'yz' -> z + z' = 1 en utilisant le postulat 5(a)
= x + x'yz'
L'implémentation logique de la fonction booléenne F2 avant simplification nécessite 9 portes logiques.
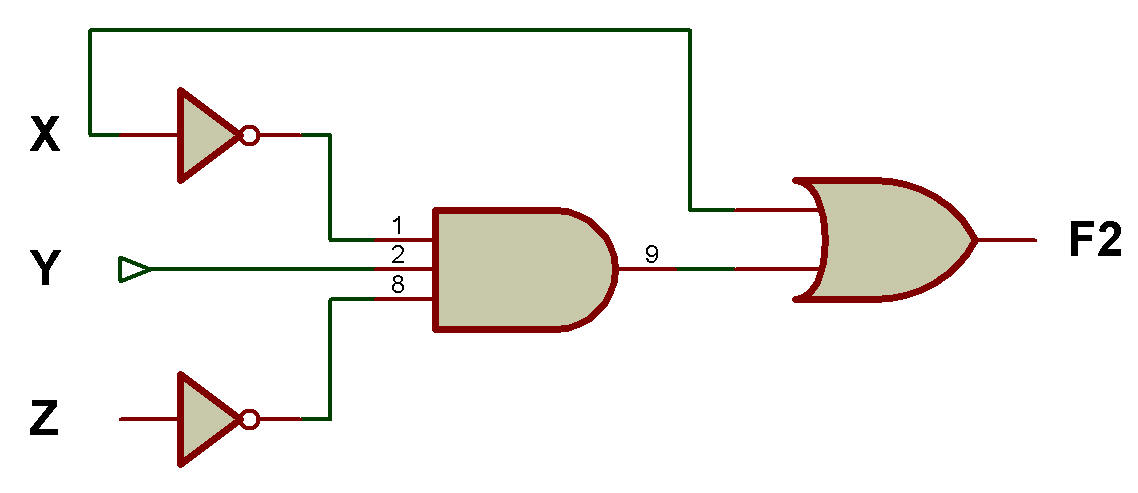
Après simplification, elle est représentée sur la figure ci-dessous et ne nécessite que 4 portes logiques.
Schéma logique pour implémenter F2 après simplification
D’après la discussion et les exemples ci-dessus, il est clair que simplifier une fonction booléenne à l’aide de la méthode algébrique n’est pas simple.
En effet, lorsque nous simplifions une fonction booléenne à l'aide d'une méthode algébrique, il n'y a pas de règle spécifique indiquant comment passer à l'étape suivante de la simplification. De nombreux théorèmes et postulats doivent également être appliqués afin de simplifier la fonction booléenne.
En dehors de cela, il n'existe aucune méthode confirmée pour savoir si la fonction booléenne réduite (fonction booléenne simplifiée) est minimisée (simplifiée) au plus petit nombre de termes [c'est-à-dire que nous ne pouvons pas dire que la fonction booléenne simplifiée ne peut pas être simplifiée davantage en appliquant d'autres théorèmes. , postulats ou manipulations algébriques].
Les deux autres méthodes, la méthode K-Map et la méthode Quine-McCluskey, sont les méthodes systématiques et directes pour simplifier les fonctions booléennes et confirment également que la fonction booléenne est simplifiée au plus petit nombre de termes (ne peut donc pas être simplifiée davantage).
Ces deux méthodes sont discutées dans les sections suivantes.
