Système de numérotation
Introduction au système numérique
L'organisation de tout ordinateur dépend considérablement de la manière dont il représente les données numériques (0, 1, 2,... .9), les données alphabétiques (A, B, C, .. .Z) et les données alphanumériques - combinaison de données alphabétiques ( A, B, C,... Z), données numériques (0,1,... 9) et caractères spéciaux (+, 6,*, etc.).
Toutes sortes de données, qu'il s'agisse d'alphabets, de chiffres, de symboles, de données sonores, de données vidéo, etc., sont représentées en termes de 0 et de 1 dans l'ordinateur.
Les systèmes numériques peuvent être globalement classés en systèmes positionnels et non positionnels. Le système le plus largement utilisé est le système de numérotation positionnelle.
Système de numérotation positionnelle
Dans un système de numérotation positionnelle, la position qu'occupe un symbole/chiffre dans le nombre détermine la valeur qu'il présente. L'idée derrière le système de numérotation positionnelle est qu'une valeur numérique est représentée par des puissances croissantes d'une base.
Ceci est souvent appelé système de numérotation pondéré car chaque position est pondérée par la puissance de la base.
Un système numérique de base b aura des symboles « b ».
Un nombre dans un système en base « b » s'écrirait en général comme suit :
![]()
a de la valeur
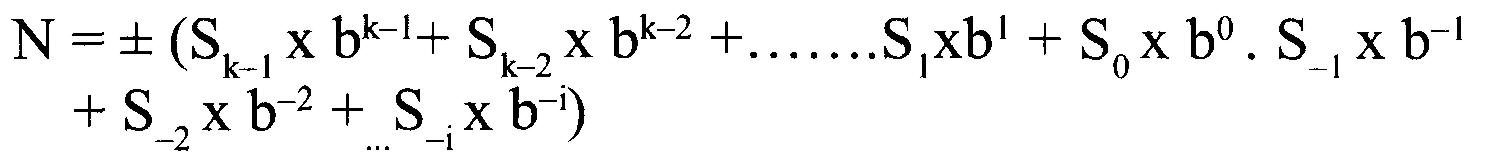
Ici:
S est l'ensemble des symboles (par exemple :
S (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) pour les nombres décimaux ;
S (0, 1, 2, 3,4, 5, 6, 7, 8, 9, A, B, C, D, E, F} pour les nombres hexadécimaux).
b est la base (ou base),
qui est égale au nombre de symboles de l'ensemble S (par exemple : les nombres
décimaux ont la base 10, les nombres octaux ont la base 8, etc.).
Sj est le symbole en position j (où j = k-1 à 0 de gauche à droite avant le « point décimal » et j = -1 à -i de droite à gauche après le « point décimal »).
k est le nombre de chiffres d'un nombre avant le « point décimal » et i est le nombre de chiffres après le « point décimal ».
Par exemple, le nombre décimal 748,63 est indiqué ci-dessous. Ici, S= (7,4,8,6,3) b=10
k = 3 (il y a 3 chiffres 7, 4 et 8 avant le « point décimal ») et i = 2 (il y a 2 chiffres 6 et 3 après le « point décimal »).
j = k-1 à 0 = 2 à 0 de gauche à droite avant le « point décimal » et j = -1 à -i = -1 à -2 de droite à gauche après le « point décimal ».
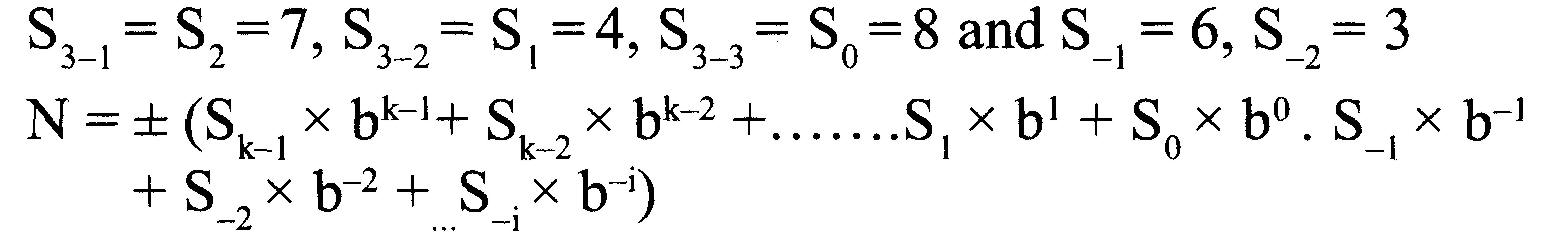
Donc,
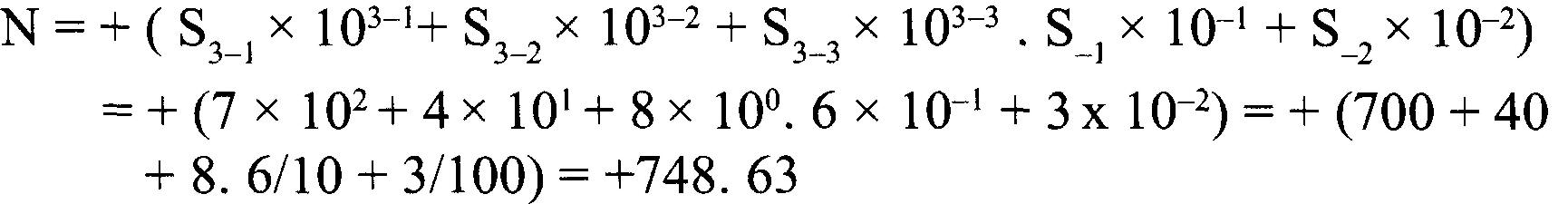
Le signe ± indique que le nombre peut être positif ou négatif.
En informatique, nous nous intéressons principalement à quatre types de systèmes numériques, comme résumé dans le tableau 1.1.
Tableau 1.1 : Types de systèmes numériques et leurs bases
| Types de systèmes numériques | Valeur de la base |
|
Système de nombres décimaux Système de nombres binaires Système de nombres octaux Système de nombres hexadécimaux |
Base 10 Base 2 Base 8 Base 16 |
Tous les systèmes numériques ci-dessus ont une partie entière et une partie réelle. Les systèmes numériques ci-dessus sont discutés un par un avec leurs parties entière et réelle.
Système de nombres décimaux (base 10)
Dans ce système, nous avons la base b=10, nous avons donc 10 symboles pour représenter un nombre.
L'ensemble S(0,1,2, 3,4, 5, 6, 7, 8, 9).
Les symboles 0, 1,2, 3,4, 5, 6, 7, 8, 9 sont appelés chiffres décimaux ou simplement chiffres.
En système décimal, un nombre s’écrit :
![]()
Par exemple, (63,29)10, -(63,29), 22,5, 34, -45, etc.
L'ordinateur stocke différemment les nombres positifs et négatifs.
Entiers
Un nombre entier dans le système décimal est un nombre sans partie fractionnaire.
Nous représentons un entier comme suit :
![]()
La valeur est calculée comme suit :
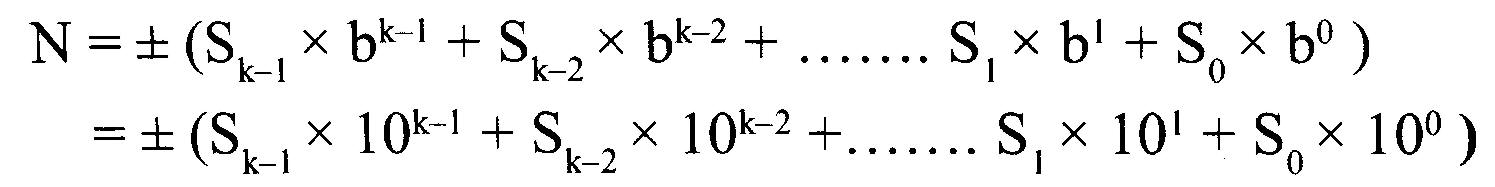
Une autre façon de représenter un entier dans un système numérique consiste à utiliser la valeur de position (également appelée valeur de position).
Les valeurs de position sont la puissance de base « b ».
Pour les nombres décimaux, la valeur de position est une puissance de 10 et est donc représentée par : 100, 101, 102, et ainsi de suite.
La figure le montre
| Position | K-1 | K-2 | ... | 2 | 1 | 0 |
| Valeur de la Position | 10K-1 | 10K-2 | ... | 102 | 101 | 100 |
Donc
N = Sk-1 x 10K-1 + Sk-2 x 10K-2 + ... S1 x 101 + S0 x 100
Exemple 1 : Entier +224 est illustré ci-dessous.
| Position | 2 | 1 | 0 |
| Valeur de la Position | 102 | 101 | 100 |
Donc
N = Sk-1 x 10K-1 + Sk-2 x 10K-2 + ... S1 x 101 + S0 x 100
N = 2 x 10² + 2 x 101 + 4 x 100 = 224
La valeur maximale d'un entier décimal peut être représentée par Nmax x = 10k- 1, où k est le nombre de chiffres.
Donc,
Avec k = 2 , Nmax x = 102- 1 = 99, cela signifie que 99 nombres peuvent être représentés.
Avec k = 3, Nmax x = 103 - 1 = 999, cela signifie que 999 nombres peuvent être représentés et ainsi de suite.
Réels
Un réel dans le système décimal est un nombre à partie fractionnaire.
Nous représentons le réel comme :
![]()
La valeur est calculée comme suit :
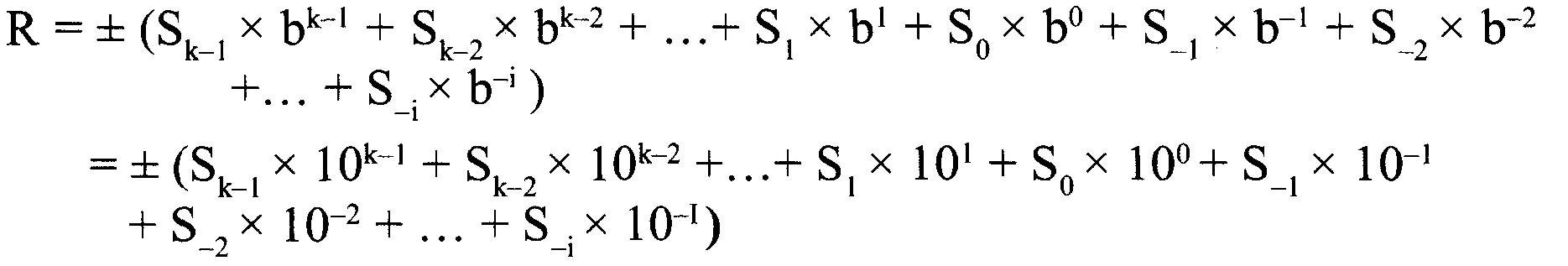
| Position | K-1 | K-2 | ... | 2 | 1 | 0 | . | -1 | -2 | ... | -i |
| Valeur de la Position | 10K-1 | 10K-2 | ... | 102 | 101 | 100 | . | 10-1 | 10-2 | ... | 10-i |
Donc
R = ± (Sk-1 x 10K-1 + Sk-2 x 10K-2 + ... S1 x 101 + S0 x 100 + S-1 x 10-1 + S-2 x 10-2 + ... + S-i x 10-i )
Exemple 2 : +24.13 est illustré ci-dessous
| 1 | 0 | . | -1 | -2 |
| 101 | 100 | . | 10-1 | 10-2 |
R = ± (2 x 10-1 + 4 x 100 + 1 x 10-1 + 3 x 10-2 = ± 24.13
Système de nombres binaires (Base 2)
Voir Aussi (Le code Binaire, Le code Binaire Suite...)
Dans le système de nombres binaires, la base b=2 et ce sont deux symboles S= (0, 1). Les symboles sont appelés chiffres binaires sous forme de bits.
Les données de l'ordinateur sont stockées sous forme binaire car l'ordinateur est constitué de commutateurs électroniques qui ne peuvent avoir que 2 états activés et désactivés.
Le bit 1 représente ON et le bit 0 représente OFF.
Entiers
Nous représentons un entier comme suit :
![]()
La valeur est calculée comme suit :
![]()
Une autre façon de représenter un entier dans un système numérique est par valeur de position (2°, 21, 2² ...).
Comme démontré ci-dessous:
| Position | K-1 | K-2 | ... | 2 | 1 | 0 |
| Valeur de la Position | 2K-1 | 2K-2 | ... | 22 | 21 | 20 |
Donc
N = Sk-1 x 2K-1 + Sk-2 x 2K-2 + ... S1 x 21 + S0 x 20
Exemple 3 : le numéro binaire 11001 est affiché ci-dessous
| Position | 4 | 3 | 2 | 1 | 0 |
| Valeur de la Position | 24 | 23 | 22 | 21 | 20 |
Donc
N = 1 x 24 + 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 16 + 8 + 0 + 0 + 1 = (25)10 = (11001)2
La valeur maximale d'un entier binaire peut être représentée par Nmax = 2k- 1, où k est le nombre de chiffres.
Donc,
Avec k = 2, Nmax = 2²- 1 = 3, soit 00, 01,10 et 11
Avec k = 3, Nmax = 2³-l = 7, soit 000, 001 010, ....,111
Réels
Un réel dans le système binaire est un nombre à partie fractionnaire.
Nous représentons le réel comme :
![]()
La valeur est calculée comme suit :
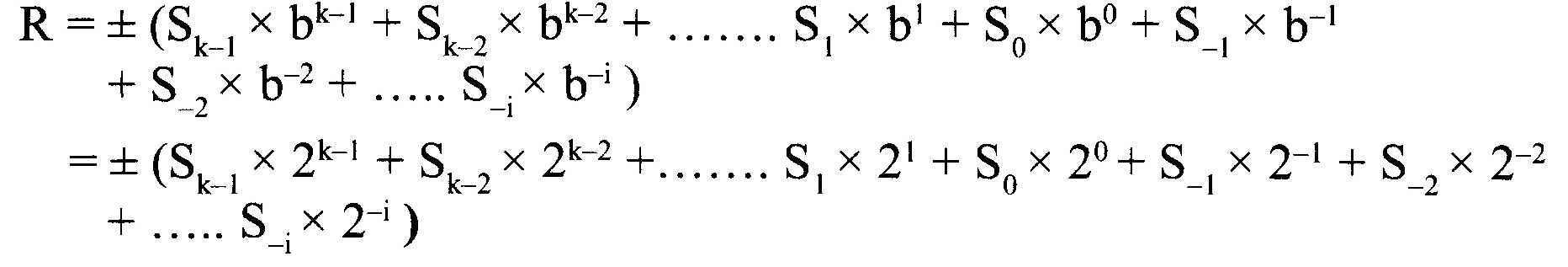
| Position | K-1 | K-2 | ... | 2 | 1 | 0 | . | -1 | -2 | ... | -i |
| Valeur de la Position | 10K-1 | 10K-2 | ... | 102 | 101 | 100 | . | 10-1 | 10-2 | ... | 10-i |
Donc
R = ± (Sk-1 x 2K-1 + Sk-2 x 2K-2 + ... S1 x 21 + S0 x 20 + S-1 x 2-1 + S-2 x 2-2 + ... + S-i x 2-i )
Exemple 4 : Le numéro 11.01 est indiqué ci-dessous :
| 1 | 0 | . | -1 | -2 |
| 21 | 20 | . | 2-1 | 2-2 |
R = (1 x 21 + 1 x 20 + 0 x 2-1 + 1 x 2-2 = 2 +1 + 0 + 1/4 = (3.25)10 = (11.01)2
Système de nombres octaux (base 8)
Ici la base b = 8 et il y a huit symboles pour représenter un nombre.
L'ensemble des symboles est S = (0, 1, 2, 3, 4, 5, 6, 7). Ces symboles sont appelés chiffres octaux.
Entiers
Nous représentons un entier comme suit :
![]()
La valeur est calculée comme suit :
![]()
Une autre façon de représenter un entier dans un système numérique est par valeur de position (80, 81, 82 ...).
| Position | K-1 | K-2 | ... | 2 | 1 | 0 |
| Valeur de la Position | 8K-1 | 8K-2 | ... | 82 | 81 | 80 |
Donc
N = Sk-1 x 8K-1 + Sk-2 x 8K-2 + ... S1 x 81 + S0 x 80
Exemple 5 : La représentation du nombre octal 1256 est présentée ci-dessous :
| Position | 3 | 2 | 1 | 0 |
| Valeur de la Position | 83 | 82 | 81 | 80 |
Donc
N = 1 x 83 + 2 x 82 + 5 x 81 + 6 x 80 = (686)10 = (1256)8
La valeur maximale d'un entier octal peut être représentée par Nmax.
Nmax= 8k-1
où k est le nombre de chiffres.
Donc, avec k = 2, Nmax = 8²-1= 63
Avec K = 5, Nmax = 85-1= 32767
Réels
Un réel dans le système octal est un nombre à partie fractionnaire. Nous représentons le réel comme :
![]()
La valeur est calculée comme suit :
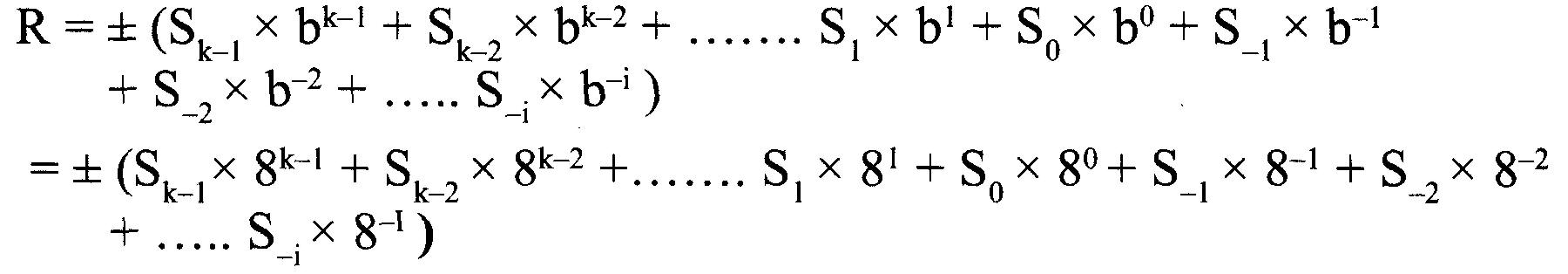
| Position | K-1 | K-2 | ... | 2 | 1 | 0 | . | -1 | -2 | ... | -i |
| Valeur de la Position | 8K-1 | 8K-2 | ... | 82 | 81 | 80 | . | 8-1 | 8-2 | ... | 8-i |
Donc
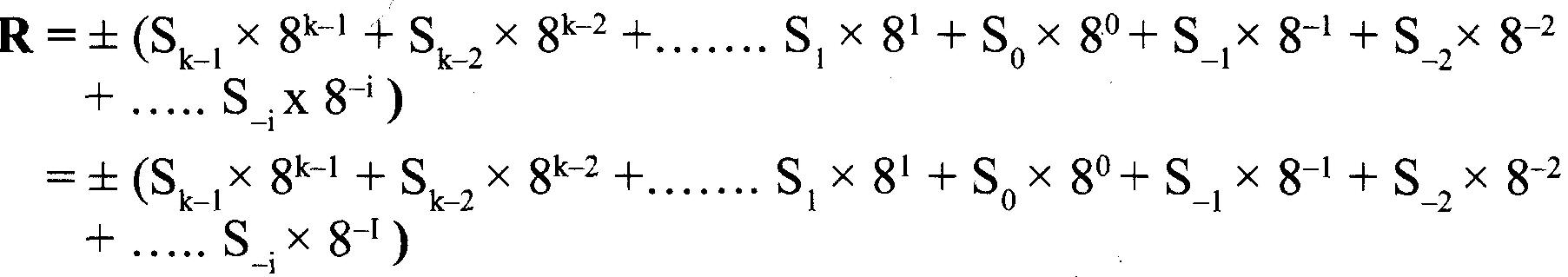
Exemple 6 : (46.72)8 est présenté ci-dessous :
| 1 | 0 | . | -1 | -2 |
| 81 | 80 | . | 8-1 | 8-2 |
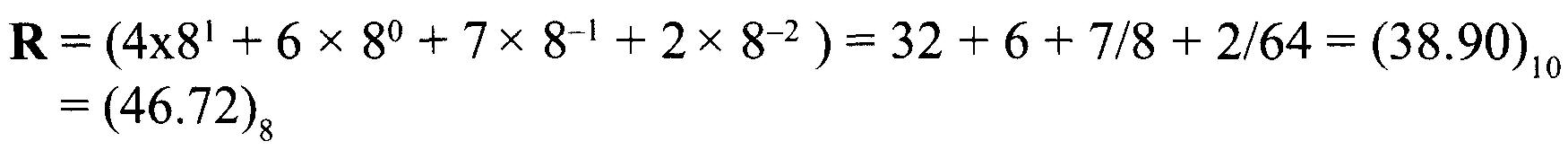
Système de nombres hexadécimaux (base 16)
Ici la base b =16, nombre de symboles=16 pour représenter un nombre.
L'ensemble des symboles est S = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Ces symboles sont appelés chiffres hexadécimaux.
Ici, A est le chiffre hexadécimal du nombre décimal 10.
Entiers
Nous représentons un entier comme suit :
![]()
La valeur est calculée comme suit :
![]()
Une autre façon de représenter un entier dans un système numérique est par valeur de position (160, 161, 16² ...).
| Position | K-1 | K-2 | ... | 2 | 1 | 0 |
| Valeur de la Position | 16K-1 | 16K-2 | ... | 162 | 161 | 160 |
Donc
N = Sk-1 x 16K-1 + Sk-2 x 16K-2 + ... S1 x 161 + S0 x 160
| Position | 2 | 1 | 0 |
| Valeur de la Position | 162 | 161 | 160 |
Donc
![]()
Exemple 7 : La représentation du nombre hexadécimal 2AE est présentée ci-dessous :
| Position | 2 | 1 | 0 |
| Valeur de la Position | 162 | 161 | 160 |
Donc
![]()
La valeur maximale d'un entier hexadécimal peut être représentée par Nmax = 16k-1, où k est le nombre de chiffres.
Donc, avec k = 5, N = 165- 1 = 1048575
Réels
Un réel dans le système hexadécimal est un nombre à partie fractionnaire. Nous représentons le réel comme :
![]()
La valeur est calculée comme suit :
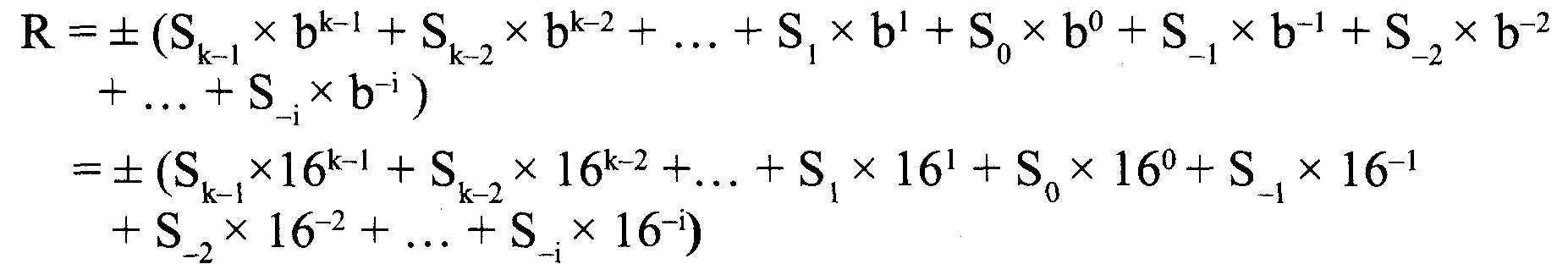
| Position | K-1 | K-2 | ... | 2 | 1 | 0 | . | -1 | -2 | ... | -i |
| Valeur de la Position | 16K-1 | 16K-2 | ... | 162 | 161 | 160 | . | 16-1 | 16-2 | ... | 16-i |
Donc
R = ±(Sk-1 x 16K-1 + Sk-2 x 16K-2 + ... S1 x 161 + S0 x 160 + S-1 x 16-1 + S-2 x 16-2 + ... + S-i x 16-i
Exemple 8 : La représentation de (A1.2E)16 est présentée ci-dessous :
| 1 | 0 | . | -1 | -2 |
| 161 | 160 | . | 16-1 | 16-2 |
R = ±( A x 161 + 1 x 160 + 2 x 16-1 + E x 16-2 = 160 + 1 + 0.125 + 0.054 = (161.179)10 = (A1.2E)16
Résumé de 4 systèmes de position
| Système | Base | Symbole | Exemple |
| Décimale | 10 | 0,1,2,3,4,5,6,7,8,9 | 234.92 |
| Binaire | 2 | 0,1 | 110.011 |
| Octal | 8 | 0,1,2,3,4,5,6,7 | 156.20 |
| Hexadécimal | 16 | 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F | AF.B2 |
